18.2.2菱形的判定 第2课时
文档属性
| 名称 | 18.2.2菱形的判定 第2课时 |  | |
| 格式 | zip | ||
| 文件大小 | 449.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 09:05:51 | ||
图片预览






文档简介
课件24张PPT。数 学新课标(RJ) 八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.2 菱形第2课时 菱形的判定教材重难处理第2课时 菱形的判定教材【第58页练习第3题】分层分析
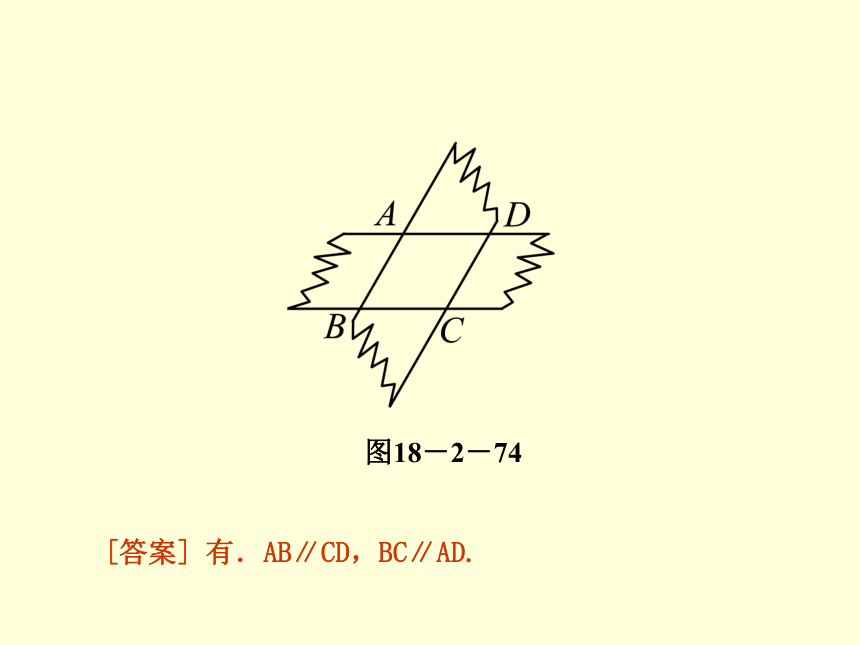
如图18-2-74,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
分析:(1)图中两张纸条的边中有平行线吗?由此说明四边形ABCD的边AB与CD,BC与AD有怎样的位置关系?第2课时 菱形的判定图18-2-74[答案] 有.AB∥CD,BC∥AD. 第2课时 菱形的判定(2)由(1)说明四边形ABCD是什么四边形?依据是什么?
[答案] 平行四边形,平行四边形的定义.
(3)“两张等宽的纸条”中的“等宽”如何理解?
[答案] 宽度相等,即纸条两平行边之间的距离相等.
(4)请过点A分别作出平行线AB与CD,平行线BC与AD之间的距离,这两个距离是纸条的宽度吗?
[答案] 作图略,是.第2课时 菱形的判定(5)结合(3),(4),你由“两张等宽的纸条”可以推出四边形ABCD的边有怎样的数量关系?为什么?
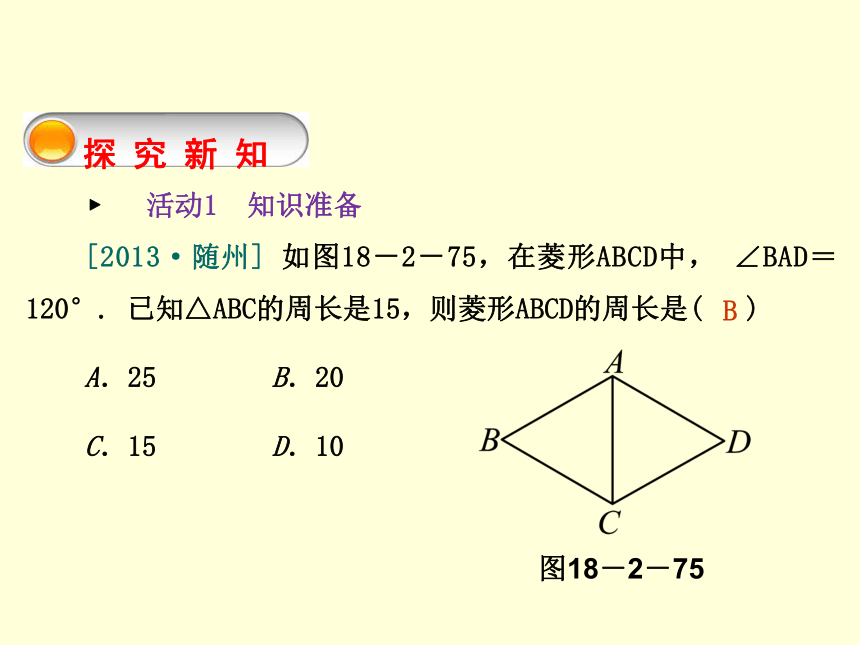
[答案] AB=BC=CD=AD,利用平行四边形的面积计算方法,面积相等,若高相等,则底边长也相等.探 究 新 知 ? 活动1 知识准备第2课时 菱形的判定[2013·随州] 如图18-2-75,在菱形ABCD中, ∠BAD=120°. 已知△ABC的周长是15,则菱形ABCD的周长是( )
A.25 B.20
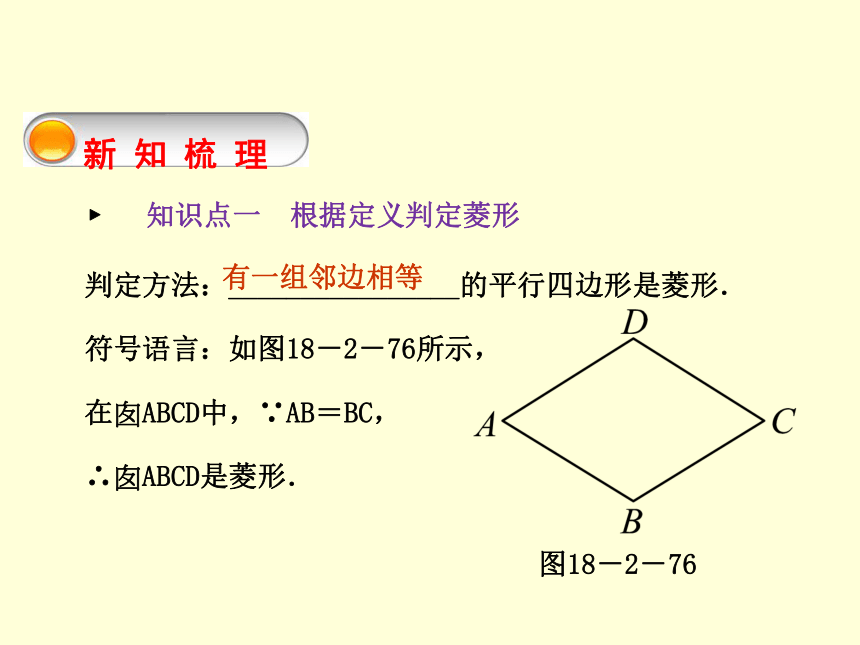
C.15 D.10图18-2-75B ? 活动2 教材导学 第2课时 菱形的判定用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个______四边形,依据是______________________________________.转动木条,当这两根木条________时,这个四边形就变成了菱形.通过这个演示,你能得到判定菱形的一个方法是_______________________________________________.平行对角线互相平分的四边形是平行四边形互相垂直对角线互相垂直的平行四边形是菱形新 知 梳 理 ? 知识点一 根据定义判定菱形第2课时 菱形的判定判定方法:________________的平行四边形是菱形.
符号语言:如图18-2-76所示,
在?ABCD中,∵AB=BC,
∴?ABCD是菱形.图18-2-76
有一组邻边相等第2课时 菱形的判定 ? 知识点二 从对角线的位置关系判定菱形 定理:对角线_____________的平行四边形是菱形.
符号语言:如图18-2-77所示,在?ABCD中,
∵AC⊥BD,
∴?ABCD是菱形.图18-2-77互相垂直第2课时 菱形的判定 ? 知识点三 从边的数量关系判定菱形 定理:四条边_______的四边形是菱形.
符号语言:如图18-2-78所示,在四边形ABCD中,
∵AB=BC=CD=DA,∴四边形ABCD是菱形. 图18-2-78相等重难互动探究探究问题一 菱形的判定第2课时 菱形的判定例1 [2013·乌鲁木齐] 如图18-2-79,在△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,分别与BC,CD交于点E,F,EH⊥AB于点H,连接FH.求证:四边形CFHE是菱形.图18-2-79第2课时 菱形的判定[解析] 方法一:(1)利用角平分线定理得CE=EH.
(2)利用Rt△ACE与Rt△AHE全等得∠AEC=∠AEH.
(3)通过平行线证CF=CE.
(4)利用一组对边平行且相等证四边形CFHE是平行四边形.
(5)因为一组邻边相等,所以?CFHE是菱形.
方法二:(1)证△ACE≌△AHE,得EC=EH,AC=AH.
(2) 证△AFC≌△AFH,得FC=FH.
(3)证∠CFE=∠CEF,得CF=CE.第2课时 菱形的判定(4)利用四条边都相等的四边形是菱形证明结论.
证明:方法一:∵AE平分∠BAC,∠ACB=90°,EH⊥AB于点H,
∴CE=EH.
在Rt△ACE与Rt△AHE中,
∵CE=EH,AE=AE,
∴Rt△ACE≌Rt△AHE,
∴∠AEC=∠AEH.
∵EH⊥AB于点H,CD⊥AB于点D,第2课时 菱形的判定∴EH∥CF,
∵∠CFE=∠AEH,
∴∠AEC=∠CFE,∴CF=CE,∴EH=CF,
∴四边形CFHE是平行四边形.
∵CF=CE,
∴四边形CFHE是菱形.
方法二:∵AE平分∠BAC,
∴∠CAE=∠HAE.
∵EH⊥AB于点H,第2课时 菱形的判定∴∠ACB=∠AHE=90°.
又∵AE=AE,∴△ACE≌△AHE,
∴EC=EH,AC=AH.
又∵∠CAE=∠HAE,AF=AF,
∴△AFC≌△AFH,
∴FC=FH.
∵CD⊥AB于点D,∠ACB=90°,
∴∠DAF+∠AFD=∠CAE+∠AEC=90°.
又∵∠DAF=∠CAE,第2课时 菱形的判定∠AFD=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE,
∴EC=EH=HF=FC,
∴四边形CFHE是菱形.第2课时 菱形的判定[归纳总结] 判定一个四边形是菱形,根据已知条件来选择方法,当已知邻边相等要证明一个四边形是菱
形,有两条路可走:(1)证明四条边都相等.(2)先证明它是平行四边形,再利用邻边相等的平行四边形是菱形来证明.
当已知条件中出现两条对角线,要证明一个四边形是菱形,可考虑利用:(1)对角线互相垂直平分的四边形是菱形.(2)对角线互相垂直的平行四边形是菱形.第2课时 菱形的判定探究问题二 菱形与矩形、平行四边形的性质的综合运用 例2 如图18-2-80所示,在四边形ABCD中,点E,F是对角线BD上的两点且BE=DF.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?为什么?
(3)若四边形AECF是矩形,试判断四边形ABCD是否为矩形,不必写理由.第2课时 菱形的判定图18-2-80第2课时 菱形的判定[解析] (1)由已知,连接AC,交BD于点O,由?AECF的对角线互相平分,证四边形ABCD的对角线互相平分.(2)(3)可类似(1)证明.第2课时 菱形的判定解:(1)证明:如图18-2-80,连接AC交EF于点O.
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF.
∵BE=DF,OB=BE+OE,OD=OF+FD,
∴OB=OD,∴四边形ABCD是平行四边形.第2课时 菱形的判定(2)四边形ABCD也是菱形.理由如下:
∵四边形AECF是菱形,
∴AC⊥EF,即AC⊥BD.
由(1)可知,四边形ABCD是平行四边形,
∴?ABCD是菱形.
(3)四边形ABCD不是矩形.第2课时 菱形的判定[归纳总结] 当已知条件主要在对角线上时,可以通过对角线互相平分证平行四边形,对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,反过来,对角线不相等的就不是矩形了.
如图18-2-74,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
分析:(1)图中两张纸条的边中有平行线吗?由此说明四边形ABCD的边AB与CD,BC与AD有怎样的位置关系?第2课时 菱形的判定图18-2-74[答案] 有.AB∥CD,BC∥AD. 第2课时 菱形的判定(2)由(1)说明四边形ABCD是什么四边形?依据是什么?
[答案] 平行四边形,平行四边形的定义.
(3)“两张等宽的纸条”中的“等宽”如何理解?
[答案] 宽度相等,即纸条两平行边之间的距离相等.
(4)请过点A分别作出平行线AB与CD,平行线BC与AD之间的距离,这两个距离是纸条的宽度吗?
[答案] 作图略,是.第2课时 菱形的判定(5)结合(3),(4),你由“两张等宽的纸条”可以推出四边形ABCD的边有怎样的数量关系?为什么?
[答案] AB=BC=CD=AD,利用平行四边形的面积计算方法,面积相等,若高相等,则底边长也相等.探 究 新 知 ? 活动1 知识准备第2课时 菱形的判定[2013·随州] 如图18-2-75,在菱形ABCD中, ∠BAD=120°. 已知△ABC的周长是15,则菱形ABCD的周长是( )
A.25 B.20
C.15 D.10图18-2-75B ? 活动2 教材导学 第2课时 菱形的判定用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个______四边形,依据是______________________________________.转动木条,当这两根木条________时,这个四边形就变成了菱形.通过这个演示,你能得到判定菱形的一个方法是_______________________________________________.平行对角线互相平分的四边形是平行四边形互相垂直对角线互相垂直的平行四边形是菱形新 知 梳 理 ? 知识点一 根据定义判定菱形第2课时 菱形的判定判定方法:________________的平行四边形是菱形.
符号语言:如图18-2-76所示,
在?ABCD中,∵AB=BC,
∴?ABCD是菱形.图18-2-76
有一组邻边相等第2课时 菱形的判定 ? 知识点二 从对角线的位置关系判定菱形 定理:对角线_____________的平行四边形是菱形.
符号语言:如图18-2-77所示,在?ABCD中,
∵AC⊥BD,
∴?ABCD是菱形.图18-2-77互相垂直第2课时 菱形的判定 ? 知识点三 从边的数量关系判定菱形 定理:四条边_______的四边形是菱形.
符号语言:如图18-2-78所示,在四边形ABCD中,
∵AB=BC=CD=DA,∴四边形ABCD是菱形. 图18-2-78相等重难互动探究探究问题一 菱形的判定第2课时 菱形的判定例1 [2013·乌鲁木齐] 如图18-2-79,在△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,分别与BC,CD交于点E,F,EH⊥AB于点H,连接FH.求证:四边形CFHE是菱形.图18-2-79第2课时 菱形的判定[解析] 方法一:(1)利用角平分线定理得CE=EH.
(2)利用Rt△ACE与Rt△AHE全等得∠AEC=∠AEH.
(3)通过平行线证CF=CE.
(4)利用一组对边平行且相等证四边形CFHE是平行四边形.
(5)因为一组邻边相等,所以?CFHE是菱形.
方法二:(1)证△ACE≌△AHE,得EC=EH,AC=AH.
(2) 证△AFC≌△AFH,得FC=FH.
(3)证∠CFE=∠CEF,得CF=CE.第2课时 菱形的判定(4)利用四条边都相等的四边形是菱形证明结论.
证明:方法一:∵AE平分∠BAC,∠ACB=90°,EH⊥AB于点H,
∴CE=EH.
在Rt△ACE与Rt△AHE中,
∵CE=EH,AE=AE,
∴Rt△ACE≌Rt△AHE,
∴∠AEC=∠AEH.
∵EH⊥AB于点H,CD⊥AB于点D,第2课时 菱形的判定∴EH∥CF,
∵∠CFE=∠AEH,
∴∠AEC=∠CFE,∴CF=CE,∴EH=CF,
∴四边形CFHE是平行四边形.
∵CF=CE,
∴四边形CFHE是菱形.
方法二:∵AE平分∠BAC,
∴∠CAE=∠HAE.
∵EH⊥AB于点H,第2课时 菱形的判定∴∠ACB=∠AHE=90°.
又∵AE=AE,∴△ACE≌△AHE,
∴EC=EH,AC=AH.
又∵∠CAE=∠HAE,AF=AF,
∴△AFC≌△AFH,
∴FC=FH.
∵CD⊥AB于点D,∠ACB=90°,
∴∠DAF+∠AFD=∠CAE+∠AEC=90°.
又∵∠DAF=∠CAE,第2课时 菱形的判定∠AFD=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE,
∴EC=EH=HF=FC,
∴四边形CFHE是菱形.第2课时 菱形的判定[归纳总结] 判定一个四边形是菱形,根据已知条件来选择方法,当已知邻边相等要证明一个四边形是菱
形,有两条路可走:(1)证明四条边都相等.(2)先证明它是平行四边形,再利用邻边相等的平行四边形是菱形来证明.
当已知条件中出现两条对角线,要证明一个四边形是菱形,可考虑利用:(1)对角线互相垂直平分的四边形是菱形.(2)对角线互相垂直的平行四边形是菱形.第2课时 菱形的判定探究问题二 菱形与矩形、平行四边形的性质的综合运用 例2 如图18-2-80所示,在四边形ABCD中,点E,F是对角线BD上的两点且BE=DF.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?为什么?
(3)若四边形AECF是矩形,试判断四边形ABCD是否为矩形,不必写理由.第2课时 菱形的判定图18-2-80第2课时 菱形的判定[解析] (1)由已知,连接AC,交BD于点O,由?AECF的对角线互相平分,证四边形ABCD的对角线互相平分.(2)(3)可类似(1)证明.第2课时 菱形的判定解:(1)证明:如图18-2-80,连接AC交EF于点O.
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF.
∵BE=DF,OB=BE+OE,OD=OF+FD,
∴OB=OD,∴四边形ABCD是平行四边形.第2课时 菱形的判定(2)四边形ABCD也是菱形.理由如下:
∵四边形AECF是菱形,
∴AC⊥EF,即AC⊥BD.
由(1)可知,四边形ABCD是平行四边形,
∴?ABCD是菱形.
(3)四边形ABCD不是矩形.第2课时 菱形的判定[归纳总结] 当已知条件主要在对角线上时,可以通过对角线互相平分证平行四边形,对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,反过来,对角线不相等的就不是矩形了.
