18.2.3 正方形
图片预览








文档简介
课件22张PPT。数 学新课标(RJ) 八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.3 正方形18.2.3 正方形探 究 新 知 ? 活动1 知识准备1.矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等B18.2.3 正方形2.已知?ABCD,(1)请添加一个条件,使之为矩形;(2)请添加一个条件,使之为菱形.
[答案] (1)答案不唯一,如∠A=90°.(2)答案不唯一,如AB=BC.18.2.3 正方形 ? 活动2 教材导学 1.操作:将一张矩形纸片沿图18-2-93中所示的箭头方向折叠,然后沿虚线剪开,所得的四边形ABCD是___________.其中的依据是有一组邻边______的_______是正方形或有一个角是_______的_______是正方形.图18-2-93正方形相等矩形直角菱形18.2.3 正方形2.(1)类比矩形、菱形的性质,你觉得正方形有哪些性质?
[答案] 正方形的四条边都相等,四个角都是直角.
(2)类比矩形、菱形的判定,你觉得什么样的图形是正方形?
[答案] 一组邻边相等的矩形是正方形,有一个角是直角的菱形是正方形.新 知 梳 理 ? 知识点一 正方形的概念 18.2.3 正方形定义:四条边都_______,四个角都是_______的四边形是正方形.相等直角18.2.3 正方形 ? 知识点二 正方形的性质 由于正方形既是矩形又是菱形,所以正方形既有矩形的性质,又有菱形的性质.
1.对边_______且________;
2.四条边都________;
3.四个角都是_______;
4.对角线______且互相_______、_______;
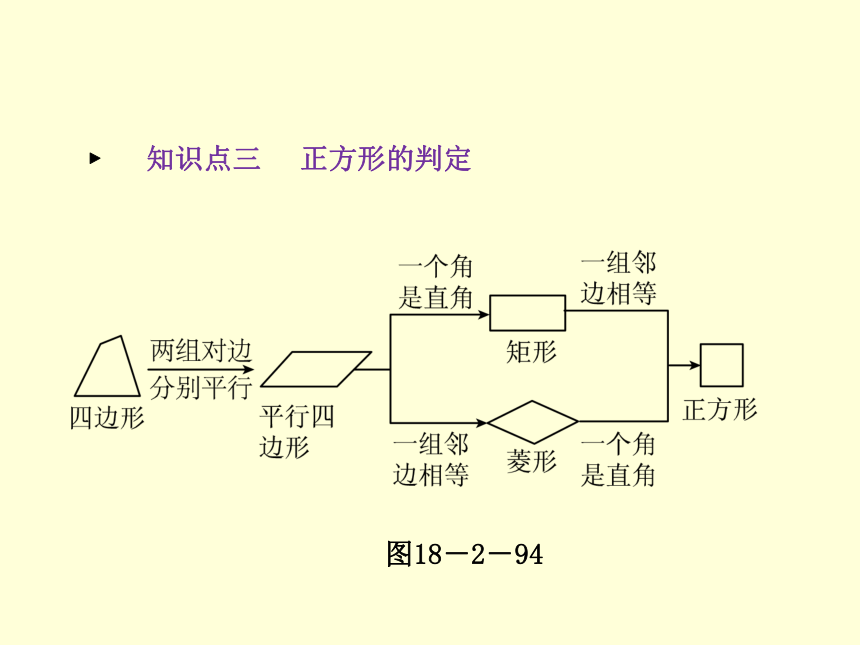
5.每一条对角线平分一组_______.平行相等相等直角相等垂直平分对角18.2.3 正方形 ? 知识点三 正方形的判定 图18-2-9418.2.3 正方形 ? 知识点四 正方形的对称性 正方形是__________图形,它共有____条对称轴. 轴对称4重难互动探究探究问题一 利用正方形的性质计算或证明 18.2.3 正方形例1 [2014·泸州] 如图18-2-95所示,正方形ABCD中,E,F分别为BC,CD上的点,且AE⊥BF,垂足为G.求证:AE=BF.图18-2-9518.2.3 正方形18.2.3 正方形例2 如图18-2-96,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB,EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.图18-2-9618.2.3 正方形[解析] 根据正方形和等边三角形的性质,得AD=DC=BC=DE=CE, ∠ADE=∠BCE=30°.然后证明△ADE≌△BCE.利用等腰三角形CBE的性质得到∠CBE的度数,然后由AD∥BC,得∠AFB=∠CBE.18.2.3 正方形解:(1)证明:∵四边形ABCD是正方形,
∴∠ADC=∠BCD=90°,AD=BC=DC.
∵△CDE是等边三角形,
∴∠CDE=∠DCE=60°,DE=CE=DC.
∵∠ADC=∠BCD=90°,
∠CDE=∠DCE=60°,
∴∠ADE=∠BCE=30°.
∵AD=BC,∠ADE=∠BCE,DE=CE,
∴△ADE≌△BCE.18.2.3 正方形(2)∵AD=BC=DC, DE=CE=DC,
∴CE=BC,
∴∠CBE=∠CEB.
∵∠BCE=30°,
∴∠CBE=∠CEB=75°.
∵四边形ABCD是正方形,
∴AD∥BC,∴∠AFB=∠CBE,
∴∠AFB=75°.18.2.3 正方形[归纳总结] 平行四边形、矩形、菱形、正方形的从属关系:
从上面的从属关系中不难看出,正方形具有平行四边形、矩形、菱形的所有性质,因此一个四边形是正方形就隐含了图形中许多相等的线段与角、互相垂直的线段、垂直平分的线段等条件.在具体问题中运用时需灵活取舍.图18-2-9718.2.3 正方形探究问题二 正方形的判定 例3如图18-2-98所示,已知?ABCD中,对角线AC,BD相交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.图18-2-9818.2.3 正方形[解析] (1)利用等边三角形三线合一得DB⊥AC,由对角线互相垂直的平行四边形是菱形可证.(2)由等边三角形得∠AEC=60°,∠AED=2∠EAD,得∠EAD=15°,于是∠ADO=∠EAD+∠AED=45°,∴∠ADC=2∠ADO=90°,从而四边形ABCD是正方形.18.2.3 正方形18.2.3 正方形18.2.3 正方形[归纳总结] 要判定一个四边形是正方形,最常用的方法就是先证明它是矩形(或菱形),再证明这个矩形(或菱形)有一组邻边相等(或有一个角是直角),其实质就是根据正方形的定义来判定,当然也可以先证四边形是平行四边形,再证有一组邻边相等,且有一个角是直角,或证这个平行四边形的对角线相等并且互相垂直.
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等B18.2.3 正方形2.已知?ABCD,(1)请添加一个条件,使之为矩形;(2)请添加一个条件,使之为菱形.
[答案] (1)答案不唯一,如∠A=90°.(2)答案不唯一,如AB=BC.18.2.3 正方形 ? 活动2 教材导学 1.操作:将一张矩形纸片沿图18-2-93中所示的箭头方向折叠,然后沿虚线剪开,所得的四边形ABCD是___________.其中的依据是有一组邻边______的_______是正方形或有一个角是_______的_______是正方形.图18-2-93正方形相等矩形直角菱形18.2.3 正方形2.(1)类比矩形、菱形的性质,你觉得正方形有哪些性质?
[答案] 正方形的四条边都相等,四个角都是直角.
(2)类比矩形、菱形的判定,你觉得什么样的图形是正方形?
[答案] 一组邻边相等的矩形是正方形,有一个角是直角的菱形是正方形.新 知 梳 理 ? 知识点一 正方形的概念 18.2.3 正方形定义:四条边都_______,四个角都是_______的四边形是正方形.相等直角18.2.3 正方形 ? 知识点二 正方形的性质 由于正方形既是矩形又是菱形,所以正方形既有矩形的性质,又有菱形的性质.
1.对边_______且________;
2.四条边都________;
3.四个角都是_______;
4.对角线______且互相_______、_______;
5.每一条对角线平分一组_______.平行相等相等直角相等垂直平分对角18.2.3 正方形 ? 知识点三 正方形的判定 图18-2-9418.2.3 正方形 ? 知识点四 正方形的对称性 正方形是__________图形,它共有____条对称轴. 轴对称4重难互动探究探究问题一 利用正方形的性质计算或证明 18.2.3 正方形例1 [2014·泸州] 如图18-2-95所示,正方形ABCD中,E,F分别为BC,CD上的点,且AE⊥BF,垂足为G.求证:AE=BF.图18-2-9518.2.3 正方形18.2.3 正方形例2 如图18-2-96,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB,EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.图18-2-9618.2.3 正方形[解析] 根据正方形和等边三角形的性质,得AD=DC=BC=DE=CE, ∠ADE=∠BCE=30°.然后证明△ADE≌△BCE.利用等腰三角形CBE的性质得到∠CBE的度数,然后由AD∥BC,得∠AFB=∠CBE.18.2.3 正方形解:(1)证明:∵四边形ABCD是正方形,
∴∠ADC=∠BCD=90°,AD=BC=DC.
∵△CDE是等边三角形,
∴∠CDE=∠DCE=60°,DE=CE=DC.
∵∠ADC=∠BCD=90°,
∠CDE=∠DCE=60°,
∴∠ADE=∠BCE=30°.
∵AD=BC,∠ADE=∠BCE,DE=CE,
∴△ADE≌△BCE.18.2.3 正方形(2)∵AD=BC=DC, DE=CE=DC,
∴CE=BC,
∴∠CBE=∠CEB.
∵∠BCE=30°,
∴∠CBE=∠CEB=75°.
∵四边形ABCD是正方形,
∴AD∥BC,∴∠AFB=∠CBE,
∴∠AFB=75°.18.2.3 正方形[归纳总结] 平行四边形、矩形、菱形、正方形的从属关系:
从上面的从属关系中不难看出,正方形具有平行四边形、矩形、菱形的所有性质,因此一个四边形是正方形就隐含了图形中许多相等的线段与角、互相垂直的线段、垂直平分的线段等条件.在具体问题中运用时需灵活取舍.图18-2-9718.2.3 正方形探究问题二 正方形的判定 例3如图18-2-98所示,已知?ABCD中,对角线AC,BD相交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.图18-2-9818.2.3 正方形[解析] (1)利用等边三角形三线合一得DB⊥AC,由对角线互相垂直的平行四边形是菱形可证.(2)由等边三角形得∠AEC=60°,∠AED=2∠EAD,得∠EAD=15°,于是∠ADO=∠EAD+∠AED=45°,∴∠ADC=2∠ADO=90°,从而四边形ABCD是正方形.18.2.3 正方形18.2.3 正方形18.2.3 正方形[归纳总结] 要判定一个四边形是正方形,最常用的方法就是先证明它是矩形(或菱形),再证明这个矩形(或菱形)有一组邻边相等(或有一个角是直角),其实质就是根据正方形的定义来判定,当然也可以先证四边形是平行四边形,再证有一组邻边相等,且有一个角是直角,或证这个平行四边形的对角线相等并且互相垂直.
