24.1.2垂直于弦的直径 同步练习(含答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1.2垂直于弦的直径 同步练习(含答案) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 568.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 19:50:05 | ||
图片预览

文档简介
24.1.2垂直于弦的直径
一、单选题
1.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.34
2.在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为
A.10 B. C.10或 D.10或
3.如图,是的弦,半径于点,且的长是( )
A. B. C. D.
4.如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心,如果使用此工具找到圆心,最少使用次数为( ).
A.1 B.2 C.3 D.4
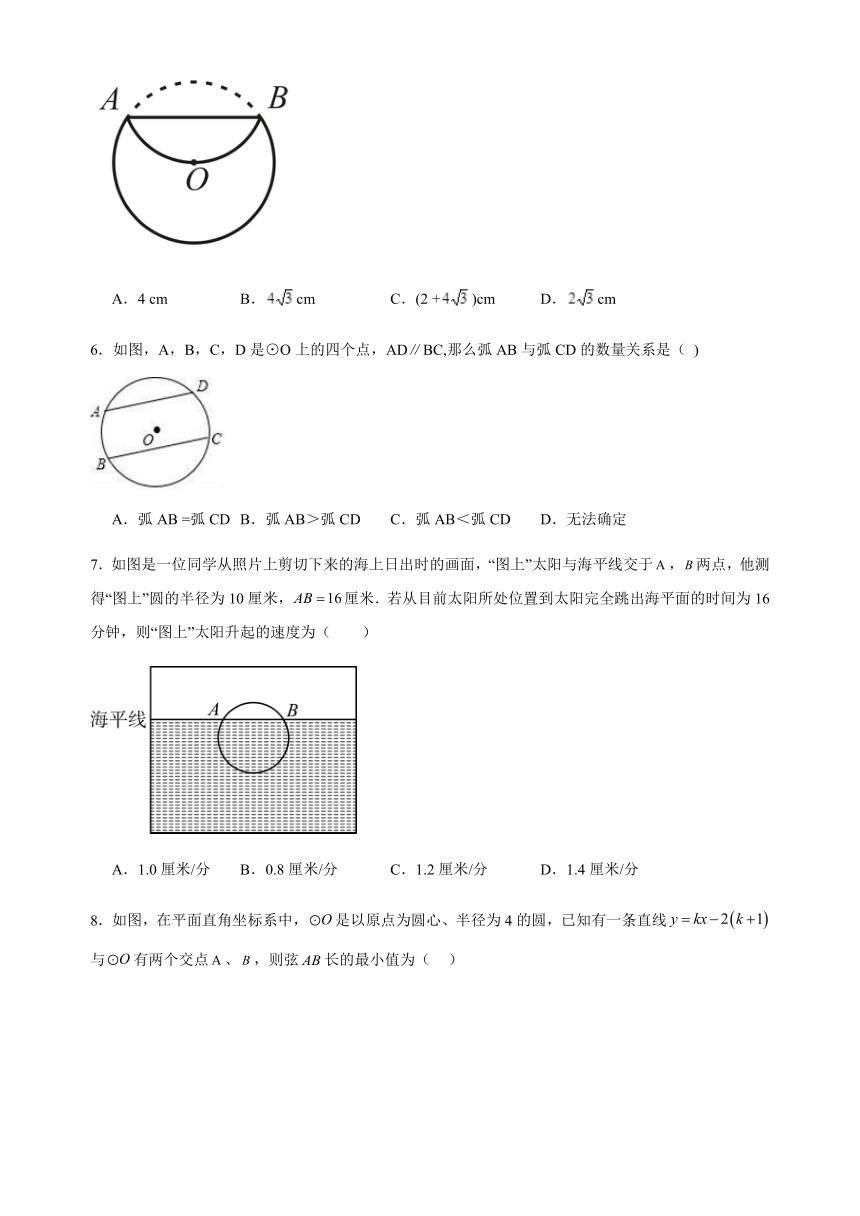
5.如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB的长度为( )
A.4 cm B.cm C.(2 +)cm D.cm
6.如图,A,B,C,D是⊙O上的四个点,AD∥BC,那么弧AB与弧CD的数量关系是( )
A.弧AB =弧CD B.弧AB>弧CD C.弧AB<弧CD D.无法确定
7.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于,两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1.4厘米/分
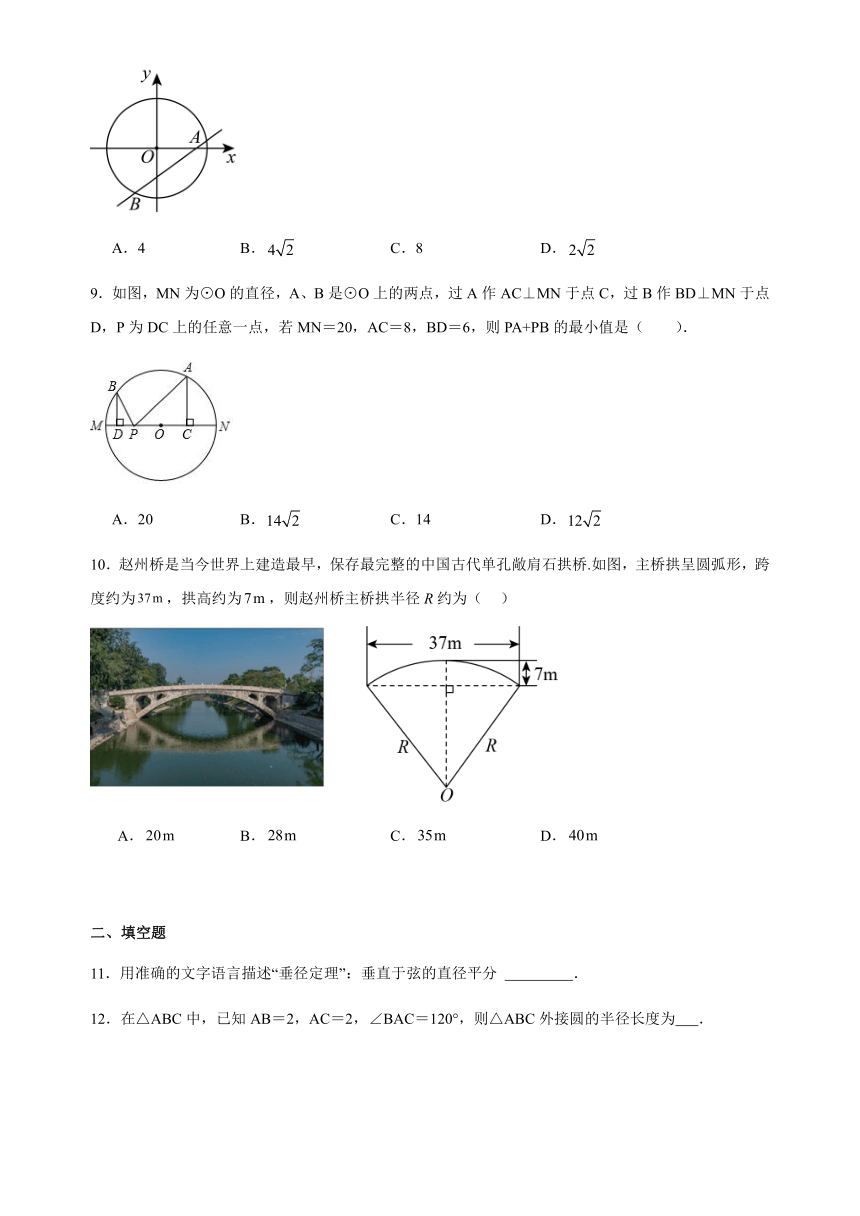
8.如图,在平面直角坐标系中,是以原点为圆心、半径为4的圆,已知有一条直线与有两个交点、,则弦长的最小值为( )
A.4 B. C.8 D.
9.如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是( ).
A.20 B. C.14 D.
10.赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为,拱高约为,则赵州桥主桥拱半径R约为( )
A. B. C. D.
二、填空题
11.用准确的文字语言描述“垂径定理”:垂直于弦的直径平分 .
12.在△ABC中,已知AB=2,AC=2,∠BAC=120°,则△ABC外接圆的半径长度为 .
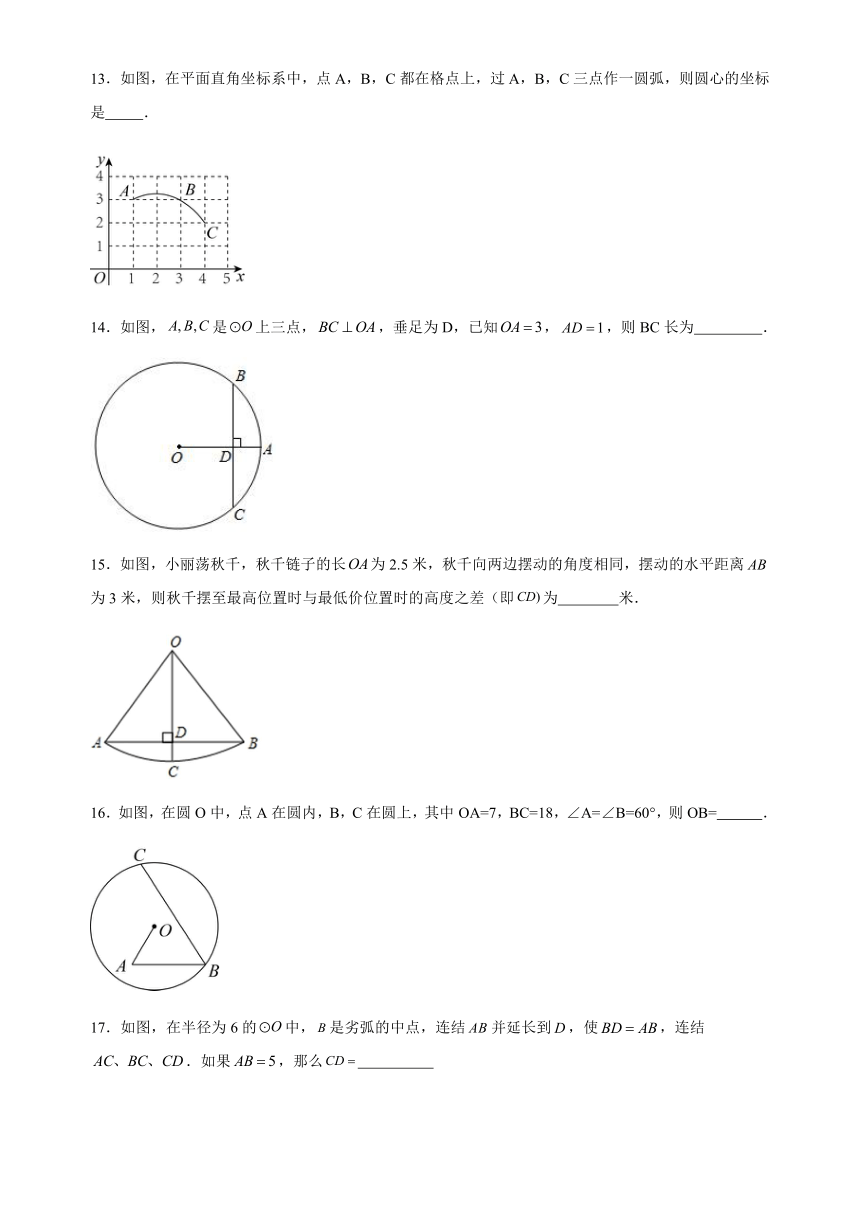
13.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
14.如图,是上三点,,垂足为D,已知,,则BC长为 .
15.如图,小丽荡秋千,秋千链子的长为2.5米,秋千向两边摆动的角度相同,摆动的水平距离为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即为 米.
16.如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB= .
17.如图,在半径为6的中,是劣弧的中点,连结并延长到,使,连结.如果,那么
三、解答题
18.《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
19.如图是一个半圆形桥洞的截面示意图,圆心为O,直径是河底线,弦是水位线,,米,于点E,此时测得.求CD的长.
20.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD,求证:AD=CD.
21.以为直径的中,为弦,分别过C、D点作的垂线,垂足分别为F、E点.
(1)如图1,若为的直径,求证:;
(2)如图2,为的非直径弦,试探究线段与间的数量关系,并说明理由.
参考答案:
1.C
2.D
3.C
4.B
5.B
6.A
7.A
8.B
9.B
10.B
11.这条弦及其所对的两条弧
12.2
13.(2,1)
14.
15.0.5/
16.
17..
18.CD=26寸.
19.米
21.
一、单选题
1.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.34
2.在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为
A.10 B. C.10或 D.10或
3.如图,是的弦,半径于点,且的长是( )
A. B. C. D.
4.如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心,如果使用此工具找到圆心,最少使用次数为( ).
A.1 B.2 C.3 D.4
5.如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB的长度为( )
A.4 cm B.cm C.(2 +)cm D.cm
6.如图,A,B,C,D是⊙O上的四个点,AD∥BC,那么弧AB与弧CD的数量关系是( )
A.弧AB =弧CD B.弧AB>弧CD C.弧AB<弧CD D.无法确定
7.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于,两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1.4厘米/分
8.如图,在平面直角坐标系中,是以原点为圆心、半径为4的圆,已知有一条直线与有两个交点、,则弦长的最小值为( )
A.4 B. C.8 D.
9.如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是( ).
A.20 B. C.14 D.
10.赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为,拱高约为,则赵州桥主桥拱半径R约为( )
A. B. C. D.
二、填空题
11.用准确的文字语言描述“垂径定理”:垂直于弦的直径平分 .
12.在△ABC中,已知AB=2,AC=2,∠BAC=120°,则△ABC外接圆的半径长度为 .
13.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
14.如图,是上三点,,垂足为D,已知,,则BC长为 .
15.如图,小丽荡秋千,秋千链子的长为2.5米,秋千向两边摆动的角度相同,摆动的水平距离为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即为 米.
16.如图,在圆O中,点A在圆内,B,C在圆上,其中OA=7,BC=18,∠A=∠B=60°,则OB= .
17.如图,在半径为6的中,是劣弧的中点,连结并延长到,使,连结.如果,那么
三、解答题
18.《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
19.如图是一个半圆形桥洞的截面示意图,圆心为O,直径是河底线,弦是水位线,,米,于点E,此时测得.求CD的长.
20.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD,求证:AD=CD.
21.以为直径的中,为弦,分别过C、D点作的垂线,垂足分别为F、E点.
(1)如图1,若为的直径,求证:;
(2)如图2,为的非直径弦,试探究线段与间的数量关系,并说明理由.
参考答案:
1.C
2.D
3.C
4.B
5.B
6.A
7.A
8.B
9.B
10.B
11.这条弦及其所对的两条弧
12.2
13.(2,1)
14.
15.0.5/
16.
17..
18.CD=26寸.
19.米
21.
同课章节目录
