2023-2024学年人教版八年级上册第十二章 《12.3角的平分线的性质》 角平分线性质的实际应用 同步训练(含答案)
文档属性
| 名称 | 2023-2024学年人教版八年级上册第十二章 《12.3角的平分线的性质》 角平分线性质的实际应用 同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 715.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 19:52:37 | ||
图片预览



文档简介
2023-2024学年人教版八年级上册第十二章
《12.3角的平分线的性质》 角平分线性质的实际应用
同步训练
一、单选题
1.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.的三条中线的交点 B.三边的垂直平分线的交点
C.三条角平分线的交点 D.三条高所在直线的交点
2.如图,在中,是它的角平分线,cm,cm,则( )
A.16:9 B.9:1 C.3:4 D.4:3
3.如图为三条两两相交的公路,某石化公司拟建立一个加油站,计划使得该加油站到三条公路的距离相等,则加油站的可选位置有( )
A.1个 B.2个 C.3个 D.4个
4.如图,是中的角平分线,于点,,,,则长是( )
A.2 B.3 C.4 D.5
5.如图,公路,公路交公路于,交公路于,若要建一汽车旅店到三条公路的距离相等,则可供选择的地址有( )
A.处 B.处 C.处 D.处
6.如图所示,在直角中,,平分交于点,且,,则的面积为( )
A.24 B.12 C.8 D.3
7.如图,O是△ABC的角平分线的交点,△ABC的面积和周长都为24,则点O到BC的距离为( )
A.1 B.2 C.3 D.4
8.如图,为的角平分线,于点,,,则的面积是( )
A.5 B.7 C.7.5 D.10
9.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①;②;③∠BDE=∠BAC;④BE=DE;⑤,其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
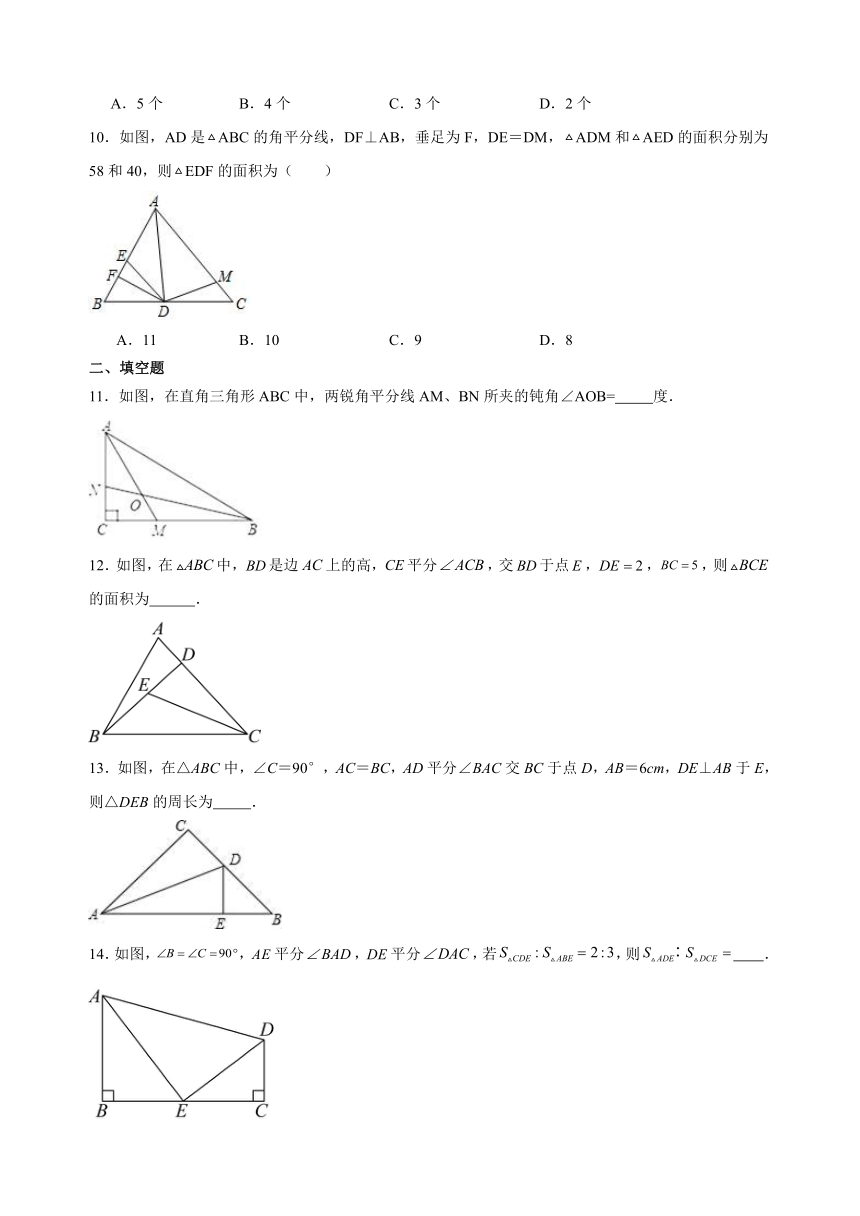
10.如图,AD是ABC的角平分线,DF⊥AB,垂足为F,DE=DM,ADM和AED的面积分别为58和40,则EDF的面积为( )
A.11 B.10 C.9 D.8
二、填空题
11.如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB= 度.
12.如图,在中,是边上的高,平分,交于点,,,则的面积为 .
13.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,AB=6cm,DE⊥AB于E,则△DEB的周长为 .
14.如图,,平分,平分,若,则 .
15.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,的面积是,则的长为
16.如图所示,已知P是△ABC三条角平分线的交点,PD⊥AB于点D,若PD=5,△ACB的周长为20,则△ABC的面积是 .
三、解答题
17.根据图片回答下列问题.
(1)如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB____DC.
(2)如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
18.太和中学校园内有一块直角三角形(RtABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
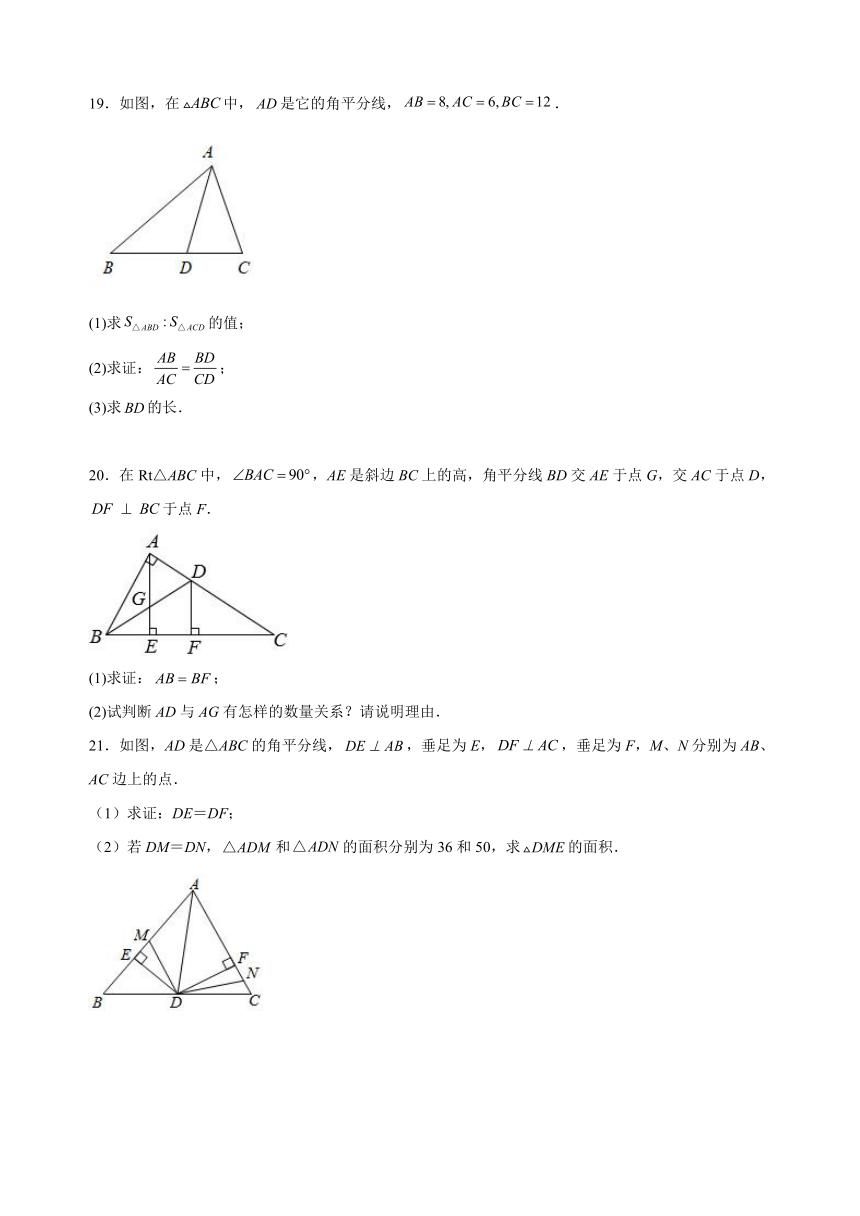
19.如图,在中,是它的角平分线,.
(1)求的值;
(2)求证:;
(3)求的长.
20.在Rt△ABC中,,AE是斜边BC上的高,角平分线BD交AE于点G,交AC于点D,于点F.
(1)求证:;
(2)试判断AD与AG有怎样的数量关系?请说明理由.
21.如图,AD是△ABC的角平分线,,垂足为E,,垂足为F,M、N分别为AB、AC边上的点.
(1)求证:DE=DF;
(2)若DM=DN,和的面积分别为36和50,求的面积.
参考答案:
1.C
【详解】解:角的平分线上的点到角的两边的距离相等,
要使凉亭到草坪三条边的距离相等,凉亭的位置应选在三条角平分线的交点.
故选:C.
2.D
【详解】解:∵是的角平分线,
∴设的边上的高与的上的高分别为
∴,
∴与的面积之比=
3.C
【详解】解:根据角平分线上的点到角两边距离相等可知,
三角形内心(即三角形内角角平分线的交点)为1个位置,
另外两外角平分线的交点,到三条公路的距离也相等,可找到3个,
但因为有1个在深水湖泊,
所以,有3个,
4.B
【详解】解:如图所示,过点作于点,
∵是中的角平分线,于点,
∴,
∵,
∴
解得:,
5.B
【详解】解:和的平分线的交点到、、距离相等,
这两个角的平分线的交点满足条件;
和的平分线的交点到、、距离相等,
这两个角的平分线的交点满足条件;
满足这条件的点有2个;
故选:B.
6.B
【详解】解:过点D作,如图
∵,,平分,
∴,
∵,
∴的面积为:;
7.B
【详解】解:设点O到BC的距离为x,
∵O是△ABC的角平分线的交点,
∴点O到AB,BC,AC的距离相等,都等于x,
∵△ABC的面积为24,周长为24,
∴,
解得:x=2.
即点O到BC的距离为2.
8.A
【详解】解:过点D作DF⊥AB,垂足为F,如图:
∵为的角平分线,于点,
∴,
∴的面积为:;
9.B
【详解】解:①正确,∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的余角相等,所以∠BDE=∠BAC;
④错误,因为∠B的度数不确定,故BE不一定等于DE;
⑤正确,因为CD=ED,△ABD和△ACD的高相等,所以S△BDE:S△ACD=BE:AC.
故正确的个数为4个.
10.C
【详解】解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DF=DH,
在Rt△DEF和Rt△DMH中,DF=DH,DE=DM,
∴Rt△DEF≌Rt△DMH(HL),
∴S△DEF=S△DMH,
∵△ADM和△AED的面积分别为58和40,
∴△EDF的面积=×(58﹣40)=9.
11.135
【详解】∵△ABC是直角三角形,
∴∠BAC+∠ABC=90°,
又∵AM,BN为∠BAC,∠ABC的角平分线,
∴∠CAM+∠NBC=45°,
∴∠AOB=180° (∠CAM+∠NBC)=135°,
∴∠AOB=135°.
12.5
【详解】解:如下图,作于F,
平分,,,
(角平分线上的点到角两边的距离相等),
,
故答案为:5
13.6cm.
【详解】∵AD平分∠BAC,DE⊥AB,∠C=90°
∴CD=ED,AC=AE
∴EB=AB-AE=AB-AC
∴△DEB的周长为ED+EB+DB=CD+DB+EB=CB+EB=BC+AB-AC=AB=6cm
14.
【详解】如图,过点作于,
∵,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
同理:,
设,,
∴,
∴,
15.4
【详解】解:如图,过点作的垂线交于点,
由题意可得:平分,
∵,
∴,
∵,的面积为,
∴,即,
∴,
∴,
故答案为:4.
16.50
【详解】作PE⊥BC于E,PF⊥AC于F,如图所示,
∵点P是△ABC三条角平分线的交点,
∴PE=PF=PD=5,
∴S△ABC=S△PAB+S△PBC+S△PAC
=PD AB+PE BC+PF AC
=(AB+BC+AC)
=×20
=50,
故答案为:50.
17.(1)=
(2)见解析
【详解】(1)∵∠B+∠C=180°,∠B=90°
∴∠C=90°
∵AD平分∠BAC
∴∠DAC=∠BAD
∵AD=AD
∴△ACD≌△ABD(AAS)
∴BD=CD
(2)如图②,在AB边上取点E,使AC=AE
∵AD平分∠BAC
∴∠CAD=∠EAD
∵AD=AD,AC=AE
∴△ACD≌△AED(SAS)
∴DC=DE,∠AED=∠C
∵∠C+∠B=180°,∠AED+∠DEB=180°
∴∠DEB=∠B
∴DE=DB
∴DB=DC
18.,
【详解】解:过点分别作,是垂足.
由,得,,
是的平分线,
.
19.(1)
(2)见解析
(3)
【详解】(1)作于点E,于点F,
∵是的角平分线,,
所以,
所以.
∴的值是.
(2)作于点G,则,
因为,
所以.
(3)因为, ,
所以.
20.(1)证明过程见详解
(2)相等,理由见详解
【详解】(1)∵BD平分∠ABC,
∴∠ABD=∠DBF,
∵DF⊥BC,
∴∠DFB=∠BAD=90°,
又∵BD=BD,
∴,
∴∠ADB=∠BDF,AB=BF;
(2)AD=AG,理由如下:
∵AE是斜边BC上的高,
∴AE⊥BC,
又∵DF⊥BC,
∴,
∴∠BGE=∠BDF,
又∵∠BGE=∠AGD,∠ADB=∠BDF,
∴∠AGD=∠ADB,
∴AG=AD.
21.(1)见解析; (2)
【详解】解:(1)证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF;
(2)在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∴.
《12.3角的平分线的性质》 角平分线性质的实际应用
同步训练
一、单选题
1.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.的三条中线的交点 B.三边的垂直平分线的交点
C.三条角平分线的交点 D.三条高所在直线的交点
2.如图,在中,是它的角平分线,cm,cm,则( )
A.16:9 B.9:1 C.3:4 D.4:3
3.如图为三条两两相交的公路,某石化公司拟建立一个加油站,计划使得该加油站到三条公路的距离相等,则加油站的可选位置有( )
A.1个 B.2个 C.3个 D.4个
4.如图,是中的角平分线,于点,,,,则长是( )
A.2 B.3 C.4 D.5
5.如图,公路,公路交公路于,交公路于,若要建一汽车旅店到三条公路的距离相等,则可供选择的地址有( )
A.处 B.处 C.处 D.处
6.如图所示,在直角中,,平分交于点,且,,则的面积为( )
A.24 B.12 C.8 D.3
7.如图,O是△ABC的角平分线的交点,△ABC的面积和周长都为24,则点O到BC的距离为( )
A.1 B.2 C.3 D.4
8.如图,为的角平分线,于点,,,则的面积是( )
A.5 B.7 C.7.5 D.10
9.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①;②;③∠BDE=∠BAC;④BE=DE;⑤,其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
10.如图,AD是ABC的角平分线,DF⊥AB,垂足为F,DE=DM,ADM和AED的面积分别为58和40,则EDF的面积为( )
A.11 B.10 C.9 D.8
二、填空题
11.如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB= 度.
12.如图,在中,是边上的高,平分,交于点,,,则的面积为 .
13.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,AB=6cm,DE⊥AB于E,则△DEB的周长为 .
14.如图,,平分,平分,若,则 .
15.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,的面积是,则的长为
16.如图所示,已知P是△ABC三条角平分线的交点,PD⊥AB于点D,若PD=5,△ACB的周长为20,则△ABC的面积是 .
三、解答题
17.根据图片回答下列问题.
(1)如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB____DC.
(2)如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
18.太和中学校园内有一块直角三角形(RtABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
19.如图,在中,是它的角平分线,.
(1)求的值;
(2)求证:;
(3)求的长.
20.在Rt△ABC中,,AE是斜边BC上的高,角平分线BD交AE于点G,交AC于点D,于点F.
(1)求证:;
(2)试判断AD与AG有怎样的数量关系?请说明理由.
21.如图,AD是△ABC的角平分线,,垂足为E,,垂足为F,M、N分别为AB、AC边上的点.
(1)求证:DE=DF;
(2)若DM=DN,和的面积分别为36和50,求的面积.
参考答案:
1.C
【详解】解:角的平分线上的点到角的两边的距离相等,
要使凉亭到草坪三条边的距离相等,凉亭的位置应选在三条角平分线的交点.
故选:C.
2.D
【详解】解:∵是的角平分线,
∴设的边上的高与的上的高分别为
∴,
∴与的面积之比=
3.C
【详解】解:根据角平分线上的点到角两边距离相等可知,
三角形内心(即三角形内角角平分线的交点)为1个位置,
另外两外角平分线的交点,到三条公路的距离也相等,可找到3个,
但因为有1个在深水湖泊,
所以,有3个,
4.B
【详解】解:如图所示,过点作于点,
∵是中的角平分线,于点,
∴,
∵,
∴
解得:,
5.B
【详解】解:和的平分线的交点到、、距离相等,
这两个角的平分线的交点满足条件;
和的平分线的交点到、、距离相等,
这两个角的平分线的交点满足条件;
满足这条件的点有2个;
故选:B.
6.B
【详解】解:过点D作,如图
∵,,平分,
∴,
∵,
∴的面积为:;
7.B
【详解】解:设点O到BC的距离为x,
∵O是△ABC的角平分线的交点,
∴点O到AB,BC,AC的距离相等,都等于x,
∵△ABC的面积为24,周长为24,
∴,
解得:x=2.
即点O到BC的距离为2.
8.A
【详解】解:过点D作DF⊥AB,垂足为F,如图:
∵为的角平分线,于点,
∴,
∴的面积为:;
9.B
【详解】解:①正确,∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的余角相等,所以∠BDE=∠BAC;
④错误,因为∠B的度数不确定,故BE不一定等于DE;
⑤正确,因为CD=ED,△ABD和△ACD的高相等,所以S△BDE:S△ACD=BE:AC.
故正确的个数为4个.
10.C
【详解】解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DF=DH,
在Rt△DEF和Rt△DMH中,DF=DH,DE=DM,
∴Rt△DEF≌Rt△DMH(HL),
∴S△DEF=S△DMH,
∵△ADM和△AED的面积分别为58和40,
∴△EDF的面积=×(58﹣40)=9.
11.135
【详解】∵△ABC是直角三角形,
∴∠BAC+∠ABC=90°,
又∵AM,BN为∠BAC,∠ABC的角平分线,
∴∠CAM+∠NBC=45°,
∴∠AOB=180° (∠CAM+∠NBC)=135°,
∴∠AOB=135°.
12.5
【详解】解:如下图,作于F,
平分,,,
(角平分线上的点到角两边的距离相等),
,
故答案为:5
13.6cm.
【详解】∵AD平分∠BAC,DE⊥AB,∠C=90°
∴CD=ED,AC=AE
∴EB=AB-AE=AB-AC
∴△DEB的周长为ED+EB+DB=CD+DB+EB=CB+EB=BC+AB-AC=AB=6cm
14.
【详解】如图,过点作于,
∵,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
同理:,
设,,
∴,
∴,
15.4
【详解】解:如图,过点作的垂线交于点,
由题意可得:平分,
∵,
∴,
∵,的面积为,
∴,即,
∴,
∴,
故答案为:4.
16.50
【详解】作PE⊥BC于E,PF⊥AC于F,如图所示,
∵点P是△ABC三条角平分线的交点,
∴PE=PF=PD=5,
∴S△ABC=S△PAB+S△PBC+S△PAC
=PD AB+PE BC+PF AC
=(AB+BC+AC)
=×20
=50,
故答案为:50.
17.(1)=
(2)见解析
【详解】(1)∵∠B+∠C=180°,∠B=90°
∴∠C=90°
∵AD平分∠BAC
∴∠DAC=∠BAD
∵AD=AD
∴△ACD≌△ABD(AAS)
∴BD=CD
(2)如图②,在AB边上取点E,使AC=AE
∵AD平分∠BAC
∴∠CAD=∠EAD
∵AD=AD,AC=AE
∴△ACD≌△AED(SAS)
∴DC=DE,∠AED=∠C
∵∠C+∠B=180°,∠AED+∠DEB=180°
∴∠DEB=∠B
∴DE=DB
∴DB=DC
18.,
【详解】解:过点分别作,是垂足.
由,得,,
是的平分线,
.
19.(1)
(2)见解析
(3)
【详解】(1)作于点E,于点F,
∵是的角平分线,,
所以,
所以.
∴的值是.
(2)作于点G,则,
因为,
所以.
(3)因为, ,
所以.
20.(1)证明过程见详解
(2)相等,理由见详解
【详解】(1)∵BD平分∠ABC,
∴∠ABD=∠DBF,
∵DF⊥BC,
∴∠DFB=∠BAD=90°,
又∵BD=BD,
∴,
∴∠ADB=∠BDF,AB=BF;
(2)AD=AG,理由如下:
∵AE是斜边BC上的高,
∴AE⊥BC,
又∵DF⊥BC,
∴,
∴∠BGE=∠BDF,
又∵∠BGE=∠AGD,∠ADB=∠BDF,
∴∠AGD=∠ADB,
∴AG=AD.
21.(1)见解析; (2)
【详解】解:(1)证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF;
(2)在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∴.
