24.2.1点和圆的位置关系巩固提升练(无答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.2.1点和圆的位置关系巩固提升练(无答案)2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 207.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 20:11:21 | ||
图片预览


文档简介
24.2.1点和圆的位置关系巩固提升练-人教版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
知识梳理
1. 点和圆的位置关系
① 点在圆内点到圆心的距离小于半径 ② 点在圆上点到圆心的距离等于半径
③ 点在圆外点到圆心的距离大于半径
2. 过三点的圆不在同一直线上的三个点确定一个圆。
3. 外接圆和外心
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆。
外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心。
一、单选题
1.用反证法证明“在中,若,则”时,应假设( )
A. B. C. D.
2.⊙O的半径为4,点P到圆心O的距离为d,如果点P在圆内,则d( )
A.d<4 B.d=4 C.d>4 D.0≤d<4
3.在平面直角坐标系中,点M的坐标为(2,0),⊙M的半径为4,则点P(-2,3)与⊙M的位置关系是( )
A.点P在⊙M内 B.点P在⊙M上
C.点P在⊙M外 D.不能确定
4.如果圆外一点P到圆上各点的最短距离为3,最长距离为9,那么这个圆的半径为( )
A.2 B.2.5 C.3 D.3.5
5.下列语句中正确的是( )
A.各边相等的多边形是正多边形 B.相等的圆心角所对的弦相等
C.经过圆心的每一条直线都是圆的对称轴 D.三点确定一个圆
6.下列命题中错误的命题为( )
A.圆既是轴对称图形,也是中心对称图形 B.在同圆或等圆中,长度相等的弧是等弧
C.三角形的外心到三角形三边距离相等 D.垂直于弦的直径平分这条弦
7.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有
A.4个 B.3个 C.2个 D.1个
8.用反证法证明“四边形中至少有一个角是钝角或直角”,可假设四边形的四个角都是( ).
A.钝角或直角 B.钝角 C.直角 D.锐角
9.下列给定的三点能确定一个圆的是( )
A.线段的中点及两个端点
B.角的顶点及角的边上的两点
C.三角形的三个顶点
D.矩形的对角线交点及两个顶点
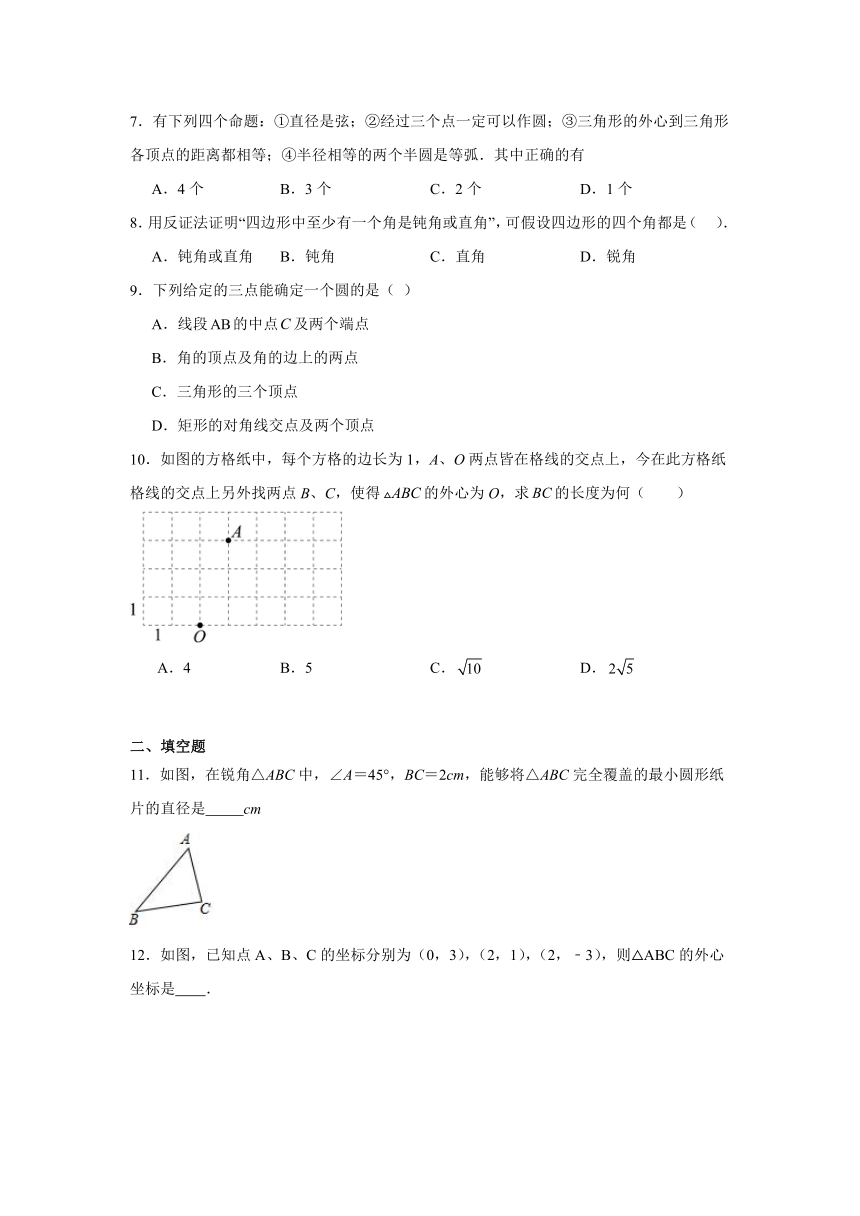
10.如图的方格纸中,每个方格的边长为1,A、O两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点B、C,使得的外心为O,求的长度为何( )
A.4 B.5 C. D.
二、填空题
11.如图,在锐角△ABC中,∠A=45°,BC=2cm,能够将△ABC完全覆盖的最小圆形纸片的直径是 cm
12.如图,已知点A、B、C的坐标分别为(0,3),(2,1),(2,﹣3),则△ABC的外心坐标是 .
13.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=8,则S△ABC= .
14.若⊙A半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P与⊙A位置关系为 .
15.用反证法证明命题“已知中,;求证:.”第一步应先假设 .
16.如图,在平面直角坐标系xOy中,点A,B的坐标分别是,,是的外接圆,则点M的坐标为 .
17.已知的半径为,点到圆心的距离为,则点与的位置关系是:点在 .(填“内”、“上”、“外”)
18.⊙O的半径为R,圆心O到点A的距离为d,且R、d分别是方程x2﹣6x+9=0的两根,则点A与⊙O的位置关系是 .
19.如图,的半径为2,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,当线段最短时,点的坐标为 .
20.中,已知,,则的外接圆半径是 .
三、解答题
21.利用反证法证明:一个三角形中不能有两个角是钝角.
22.(1)如图1,已知线段a,请用无刻度的直尺和圆规作Rt△ABC,使斜边AB=a,∠A=30°;
(2)如图2,已知矩形MNPQ中,MN=6,若在边PQ上存在一点D,使∠MDN=30°,则边NP长度的取值范围是 .
四、作图题
23.尺规作图蕴含丰富的推理,还体现逆向思维,请尝试用无刻度的直尺和圆规完成下列作图,不写作法,保留作图痕迹.
(1)【圆的作图】点P是中边上的一点,在图1中作,使它与的两边相切,点P是其中一个切点;
(2)点P是中边上的一点,在图2中作,使它满足以下条件:
①圆心O在上;②经过点P;③与边相切;
(3)【不可及点的作图】如图3,从墙边上引两条不平行的射线(交点在墙的另一侧,画不到),作这两条射线所形成角的平分线.
24.如图,已知△ABC.
(1)作△ABC的外接圆,并在AB的上方作弦AD,使AD=BC.(要求尺规作图,保留作图痕迹,不写作法)
(2)连结CD,求证:CD∥AB.
25.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,4)、B(1,1)、C(4,2).
(1)画出△ABC绕点B逆时针旋转90°后得到的△A1BC1,其中A、C分别和A1、C1
对应.
(2)平移△ABC,使得A点落在x轴上,B点落在y轴上,画出平移后的△A2B2C2,其中A、B、C分别和A2B2C2对应.
(3)填空:在(2)的条件下,设△ABC,△A2B2C2的外接圆的圆心分别为M、M2,则MM2= .
学校:___________姓名:___________班级:___________考号:___________
知识梳理
1. 点和圆的位置关系
① 点在圆内点到圆心的距离小于半径 ② 点在圆上点到圆心的距离等于半径
③ 点在圆外点到圆心的距离大于半径
2. 过三点的圆不在同一直线上的三个点确定一个圆。
3. 外接圆和外心
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆。
外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心。
一、单选题
1.用反证法证明“在中,若,则”时,应假设( )
A. B. C. D.
2.⊙O的半径为4,点P到圆心O的距离为d,如果点P在圆内,则d( )
A.d<4 B.d=4 C.d>4 D.0≤d<4
3.在平面直角坐标系中,点M的坐标为(2,0),⊙M的半径为4,则点P(-2,3)与⊙M的位置关系是( )
A.点P在⊙M内 B.点P在⊙M上
C.点P在⊙M外 D.不能确定
4.如果圆外一点P到圆上各点的最短距离为3,最长距离为9,那么这个圆的半径为( )
A.2 B.2.5 C.3 D.3.5
5.下列语句中正确的是( )
A.各边相等的多边形是正多边形 B.相等的圆心角所对的弦相等
C.经过圆心的每一条直线都是圆的对称轴 D.三点确定一个圆
6.下列命题中错误的命题为( )
A.圆既是轴对称图形,也是中心对称图形 B.在同圆或等圆中,长度相等的弧是等弧
C.三角形的外心到三角形三边距离相等 D.垂直于弦的直径平分这条弦
7.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有
A.4个 B.3个 C.2个 D.1个
8.用反证法证明“四边形中至少有一个角是钝角或直角”,可假设四边形的四个角都是( ).
A.钝角或直角 B.钝角 C.直角 D.锐角
9.下列给定的三点能确定一个圆的是( )
A.线段的中点及两个端点
B.角的顶点及角的边上的两点
C.三角形的三个顶点
D.矩形的对角线交点及两个顶点
10.如图的方格纸中,每个方格的边长为1,A、O两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点B、C,使得的外心为O,求的长度为何( )
A.4 B.5 C. D.
二、填空题
11.如图,在锐角△ABC中,∠A=45°,BC=2cm,能够将△ABC完全覆盖的最小圆形纸片的直径是 cm
12.如图,已知点A、B、C的坐标分别为(0,3),(2,1),(2,﹣3),则△ABC的外心坐标是 .
13.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=8,则S△ABC= .
14.若⊙A半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P与⊙A位置关系为 .
15.用反证法证明命题“已知中,;求证:.”第一步应先假设 .
16.如图,在平面直角坐标系xOy中,点A,B的坐标分别是,,是的外接圆,则点M的坐标为 .
17.已知的半径为,点到圆心的距离为,则点与的位置关系是:点在 .(填“内”、“上”、“外”)
18.⊙O的半径为R,圆心O到点A的距离为d,且R、d分别是方程x2﹣6x+9=0的两根,则点A与⊙O的位置关系是 .
19.如图,的半径为2,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,当线段最短时,点的坐标为 .
20.中,已知,,则的外接圆半径是 .
三、解答题
21.利用反证法证明:一个三角形中不能有两个角是钝角.
22.(1)如图1,已知线段a,请用无刻度的直尺和圆规作Rt△ABC,使斜边AB=a,∠A=30°;
(2)如图2,已知矩形MNPQ中,MN=6,若在边PQ上存在一点D,使∠MDN=30°,则边NP长度的取值范围是 .
四、作图题
23.尺规作图蕴含丰富的推理,还体现逆向思维,请尝试用无刻度的直尺和圆规完成下列作图,不写作法,保留作图痕迹.
(1)【圆的作图】点P是中边上的一点,在图1中作,使它与的两边相切,点P是其中一个切点;
(2)点P是中边上的一点,在图2中作,使它满足以下条件:
①圆心O在上;②经过点P;③与边相切;
(3)【不可及点的作图】如图3,从墙边上引两条不平行的射线(交点在墙的另一侧,画不到),作这两条射线所形成角的平分线.
24.如图,已知△ABC.
(1)作△ABC的外接圆,并在AB的上方作弦AD,使AD=BC.(要求尺规作图,保留作图痕迹,不写作法)
(2)连结CD,求证:CD∥AB.
25.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,4)、B(1,1)、C(4,2).
(1)画出△ABC绕点B逆时针旋转90°后得到的△A1BC1,其中A、C分别和A1、C1
对应.
(2)平移△ABC,使得A点落在x轴上,B点落在y轴上,画出平移后的△A2B2C2,其中A、B、C分别和A2B2C2对应.
(3)填空:在(2)的条件下,设△ABC,△A2B2C2的外接圆的圆心分别为M、M2,则MM2= .
同课章节目录
