24.2.2直线和圆的位置关系巩固提升练(无答案)2023-2024 人教版数学九年级上册
文档属性
| 名称 | 24.2.2直线和圆的位置关系巩固提升练(无答案)2023-2024 人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 406.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 20:12:39 | ||
图片预览



文档简介
24.2.2直线和圆的位置关系巩固提升练-人教版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
知识梳理
1. 直线和圆的位置关系
相交:直线和圆有两个公共点叫这条直线和圆相交,这条直线叫做圆的割线。
相切:直线和圆有一个公共点叫这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点。
相离:直线和圆没有公共点叫这条直线和圆相离。
2. 直线和圆位置关系的性质和判定
如果⊙O的半径为r,圆心O到直线的距离为d,那么
① 直线和⊙O相交;② 直线和⊙O相切;③ 直线和⊙O相离。
圆和圆
定义:
两个圆没有公共点且每个圆的点都在另一个圆的外部时,叫做这两个圆的外离。
两个圆有唯一的公共点且除了这个公共点外,每个圆上的点都在另一个圆的外部,叫做两个圆的外切。
两个圆有两个交点,叫做两个圆的相交。
两个圆有唯一的公共点且除了这个公共点外,每个圆上的点都在另一个圆的内部,叫做两个圆的内切。
两个圆没有公共点且每个圆的点都在另一个圆的内部时,叫做这两个圆的内含。
原理:
圆心距和半径的数量关系:
两圆外离<=> d>R+r 两圆外切<=> d=R+r
两圆相交<=> R-r=r) 两圆内切<=> d=R-r(R>r)
两圆内含<=> dr)
一、单选题
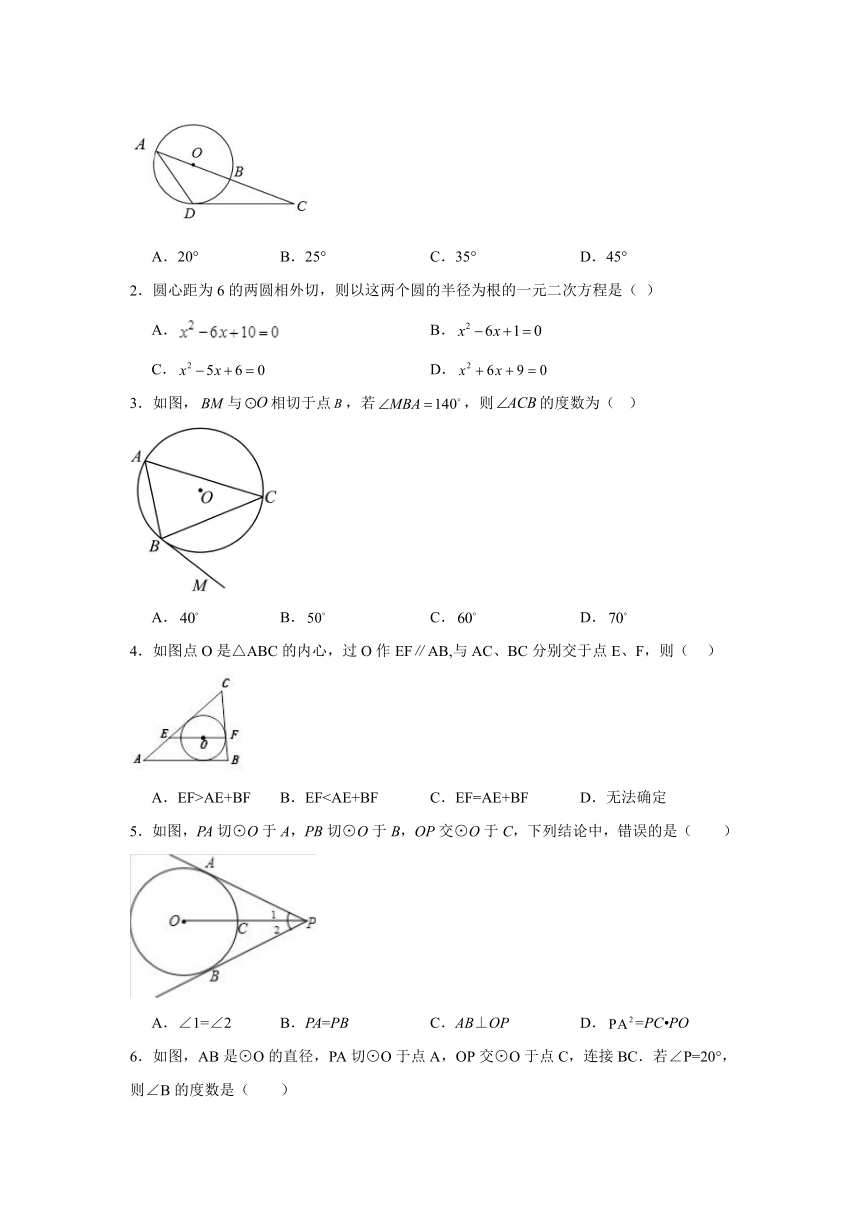
1.如图,AB是⊙O的直径,点C在AB延长线上,CD与⊙O相切于点D,连接AD,若∠ACD=20°,则∠CAD的度数等于( )
A.20° B.25° C.35° D.45°
2.圆心距为6的两圆相外切,则以这两个圆的半径为根的一元二次方程是( )
A. B.
C. D.
3.如图,与相切于点,若,则的度数为( )
A. B. C. D.
4.如图点O是△ABC的内心,过O作EF∥AB,与AC、BC分别交于点E、F,则( )
A.EF>AE+BF B.EF5.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.=PC PO
6.如图,AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC.若∠P=20°,则∠B的度数是( )
A.20° B.25° C.30° D.35°
7.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切.点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为( )
A.(0,9) B.(0,10) C.(0,11) D.(0,12)
8.如图,从外一点A作的切线AB,切点为B,连接AO并延长交于点C,连接BC.若,则∠ACB的度数是( )
A.26° B.30° C.32° D.36°
9.如图,AB切⊙O于点B,OA交⊙O于点C,过点B作BD∥AO交⊙O于点D,连接CD.若∠DCO=25°,则∠A的度数为( )
A.35° B.40° C.50° D.55°
10.如图,和是的两条切线,切点分别是A、B,点C在线段上,与交于点D,若,,则的度数为( )
A. B. C. D.
二、填空题
11.直径为 10cm 的圆,若该圆的圆心到直线的距离为 4cm,则该直线与圆的公共点个数为 个.
12.如图,等边内切圆的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称.若等边的边长为6,则圆中的黑色部分的面积是 .
13.菱形四边的中点到 的距离相等,因此菱形各边的中点在以 为圆心,以 为半径的圆上.
14.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
15.如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连BC.若∠P=30°,则∠B= °.
16.已知等边三角形的边长为,则它的内切圆的半径为 .
17.如图,是的内切圆,,则的大小是 .
18.已知:如图,三角形内接于,为直径,过点作直线,要使得是的切线,还需添加的条件是(只需写出三种):① 或② 或③ .
19.如图所示的网格是正方形网格,线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,则α的值为 .
20.如图,已知∠APB=30°,O是线段PB上的一点,OP=5cm,若以点O为圆心,1.5cm为半径的⊙O沿BP方向以1cm/s的速度移动,则⊙O移动 s后与PA相切.
三、解答题
21.如图,△ABC内接于⊙O,AB为直径,延长BA至点P使AP=AC,连接PC,∠P=30°,作CD平分∠ACB交AB于点E,交⊙O于点D
(1)求证:PC为⊙O的切线;
(2)连接BD,求证:BD=PA.
22.如图,以的边上一点为圆心的圆,经过两点,且与边交于点为的下半圆弧的中点,连接交于,若.
(1)求证:是的切线;
(2)若,,求的半径.
23.如图,为的直径,平分,交于点,过点作直线,交的延长线于点,交的延长线于点
(1)求证:是的切线
(2)若,,求的长
24.如图,矩形中,=13,=6,点E是上的动点,以为直径的⊙O与交于点F,过点F作于点G.
(1)当E是的中点时:tan的值.
(2)在(1)的条件下,证明:是圆O的切线.
25.如图,已知,.
(1)在图中,用尺规作出的内切圆O,并标出与边,,的切点D,E,F(保留痕迹,不必写作法);
(2)连接,,求的度数.
学校:___________姓名:___________班级:___________考号:___________
知识梳理
1. 直线和圆的位置关系
相交:直线和圆有两个公共点叫这条直线和圆相交,这条直线叫做圆的割线。
相切:直线和圆有一个公共点叫这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点。
相离:直线和圆没有公共点叫这条直线和圆相离。
2. 直线和圆位置关系的性质和判定
如果⊙O的半径为r,圆心O到直线的距离为d,那么
① 直线和⊙O相交;② 直线和⊙O相切;③ 直线和⊙O相离。
圆和圆
定义:
两个圆没有公共点且每个圆的点都在另一个圆的外部时,叫做这两个圆的外离。
两个圆有唯一的公共点且除了这个公共点外,每个圆上的点都在另一个圆的外部,叫做两个圆的外切。
两个圆有两个交点,叫做两个圆的相交。
两个圆有唯一的公共点且除了这个公共点外,每个圆上的点都在另一个圆的内部,叫做两个圆的内切。
两个圆没有公共点且每个圆的点都在另一个圆的内部时,叫做这两个圆的内含。
原理:
圆心距和半径的数量关系:
两圆外离<=> d>R+r 两圆外切<=> d=R+r
两圆相交<=> R-r
两圆内含<=> d
一、单选题
1.如图,AB是⊙O的直径,点C在AB延长线上,CD与⊙O相切于点D,连接AD,若∠ACD=20°,则∠CAD的度数等于( )
A.20° B.25° C.35° D.45°
2.圆心距为6的两圆相外切,则以这两个圆的半径为根的一元二次方程是( )
A. B.
C. D.
3.如图,与相切于点,若,则的度数为( )
A. B. C. D.
4.如图点O是△ABC的内心,过O作EF∥AB,与AC、BC分别交于点E、F,则( )
A.EF>AE+BF B.EF
A.∠1=∠2 B.PA=PB C.AB⊥OP D.=PC PO
6.如图,AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC.若∠P=20°,则∠B的度数是( )
A.20° B.25° C.30° D.35°
7.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切.点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为( )
A.(0,9) B.(0,10) C.(0,11) D.(0,12)
8.如图,从外一点A作的切线AB,切点为B,连接AO并延长交于点C,连接BC.若,则∠ACB的度数是( )
A.26° B.30° C.32° D.36°
9.如图,AB切⊙O于点B,OA交⊙O于点C,过点B作BD∥AO交⊙O于点D,连接CD.若∠DCO=25°,则∠A的度数为( )
A.35° B.40° C.50° D.55°
10.如图,和是的两条切线,切点分别是A、B,点C在线段上,与交于点D,若,,则的度数为( )
A. B. C. D.
二、填空题
11.直径为 10cm 的圆,若该圆的圆心到直线的距离为 4cm,则该直线与圆的公共点个数为 个.
12.如图,等边内切圆的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称.若等边的边长为6,则圆中的黑色部分的面积是 .
13.菱形四边的中点到 的距离相等,因此菱形各边的中点在以 为圆心,以 为半径的圆上.
14.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
15.如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连BC.若∠P=30°,则∠B= °.
16.已知等边三角形的边长为,则它的内切圆的半径为 .
17.如图,是的内切圆,,则的大小是 .
18.已知:如图,三角形内接于,为直径,过点作直线,要使得是的切线,还需添加的条件是(只需写出三种):① 或② 或③ .
19.如图所示的网格是正方形网格,线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,则α的值为 .
20.如图,已知∠APB=30°,O是线段PB上的一点,OP=5cm,若以点O为圆心,1.5cm为半径的⊙O沿BP方向以1cm/s的速度移动,则⊙O移动 s后与PA相切.
三、解答题
21.如图,△ABC内接于⊙O,AB为直径,延长BA至点P使AP=AC,连接PC,∠P=30°,作CD平分∠ACB交AB于点E,交⊙O于点D
(1)求证:PC为⊙O的切线;
(2)连接BD,求证:BD=PA.
22.如图,以的边上一点为圆心的圆,经过两点,且与边交于点为的下半圆弧的中点,连接交于,若.
(1)求证:是的切线;
(2)若,,求的半径.
23.如图,为的直径,平分,交于点,过点作直线,交的延长线于点,交的延长线于点
(1)求证:是的切线
(2)若,,求的长
24.如图,矩形中,=13,=6,点E是上的动点,以为直径的⊙O与交于点F,过点F作于点G.
(1)当E是的中点时:tan的值.
(2)在(1)的条件下,证明:是圆O的切线.
25.如图,已知,.
(1)在图中,用尺规作出的内切圆O,并标出与边,,的切点D,E,F(保留痕迹,不必写作法);
(2)连接,,求的度数.
同课章节目录
