13.3.2等边三角形同步练习(含答案)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 13.3.2等边三角形同步练习(含答案)2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 365.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 20:42:46 | ||
图片预览


文档简介
13.3.2等边三角形同步练习
2023—2024学年人教版数学八年级上册
一、单选题
1.等边三角形是( ).
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰直角三角形
2.正三角形的边长为4,AD是BC边上的高,则BD是( ).
A.1 B.2 C.3 D.4
3.如图,直线,△ABC是等边三角形,若,则的度数为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,∠A=15°,AB的垂直平分线与AC交于点M,则BC与MB的比为( )
A.1:3 B.1:2 C.2:3 D.3:4
5.如图所示,已知△ABC是等边三角形,点是上任意一点,,分别于两边垂直,等边三角形的高为1,则的值为( )
A. B.1 C.2 D.不确定
6.如图,D是等边△ABC的边AC上的一点,E是等边△ABC外一点,若,
,则对△ADE的形状最准确的是( ).
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
7.如图,已知将△ABE沿所在直线翻折,点恰好与上的点重合,对折边,折痕也经过点,则下列说法正确的是( )
①;
②;
③;
④S△ACD:S △ACE= ;
⑤若,则△ABC是等边三角形.
A.只有①②正确 B.①②③
C.①②③④ D.①②③④⑤
8.如图,∠AOB=120°,OP平分∠AOB,且OP=2,若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
A.2个 B.3个 C.4个 D.无数个
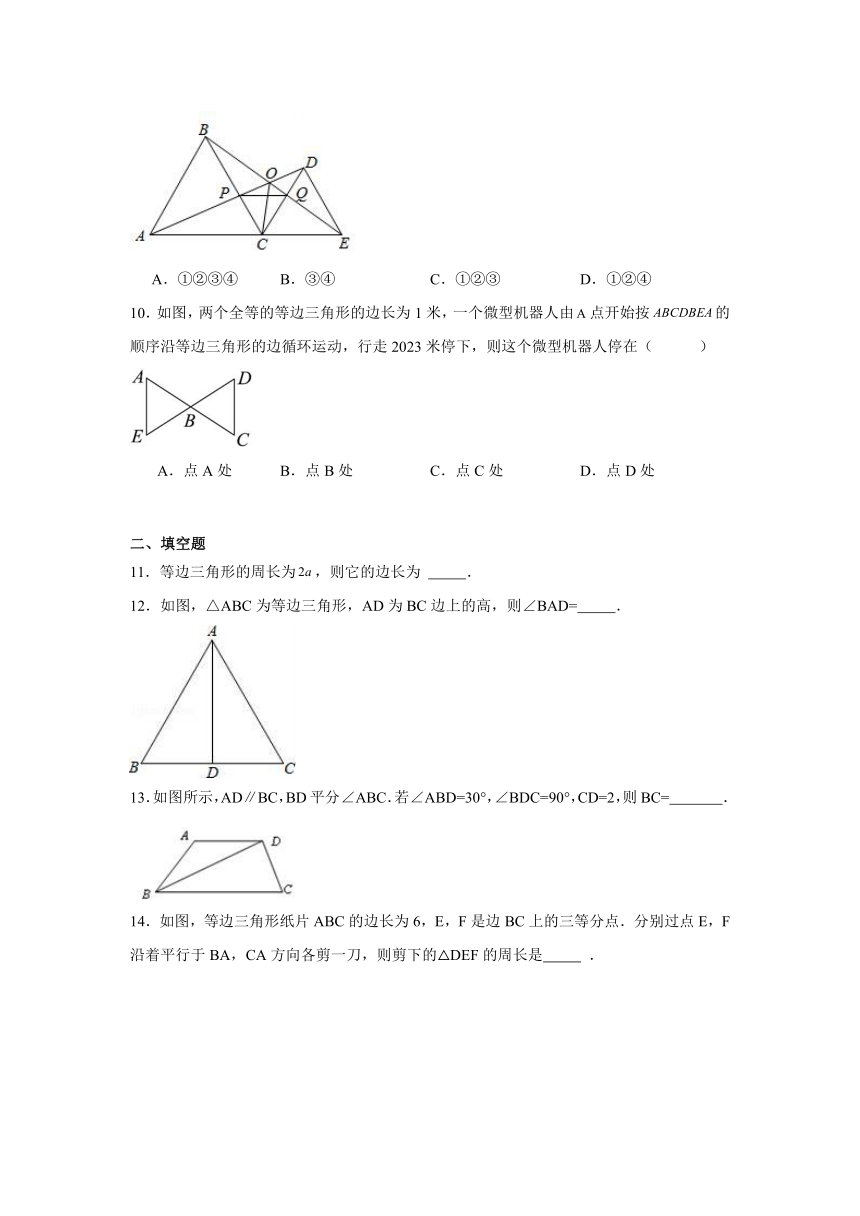
9.已知如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下四个结论:①AD=BE;②△CPQ是等边三角形;③AD⊥BC;④OC平分∠AOE.其中正确的结论是( )
A.①②③④ B.③④ C.①②③ D.①②④
10.如图,两个全等的等边三角形的边长为1米,一个微型机器人由点开始按的顺序沿等边三角形的边循环运动,行走2023米停下,则这个微型机器人停在( )
A.点A处 B.点B处 C.点C处 D.点D处
二、填空题
11.等边三角形的周长为,则它的边长为 .
12.如图,△ABC为等边三角形,AD为BC边上的高,则∠BAD= .
13.如图所示,AD∥BC,BD平分∠ABC.若∠ABD=30°,∠BDC=90°,CD=2,则BC= .
14.如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是 .
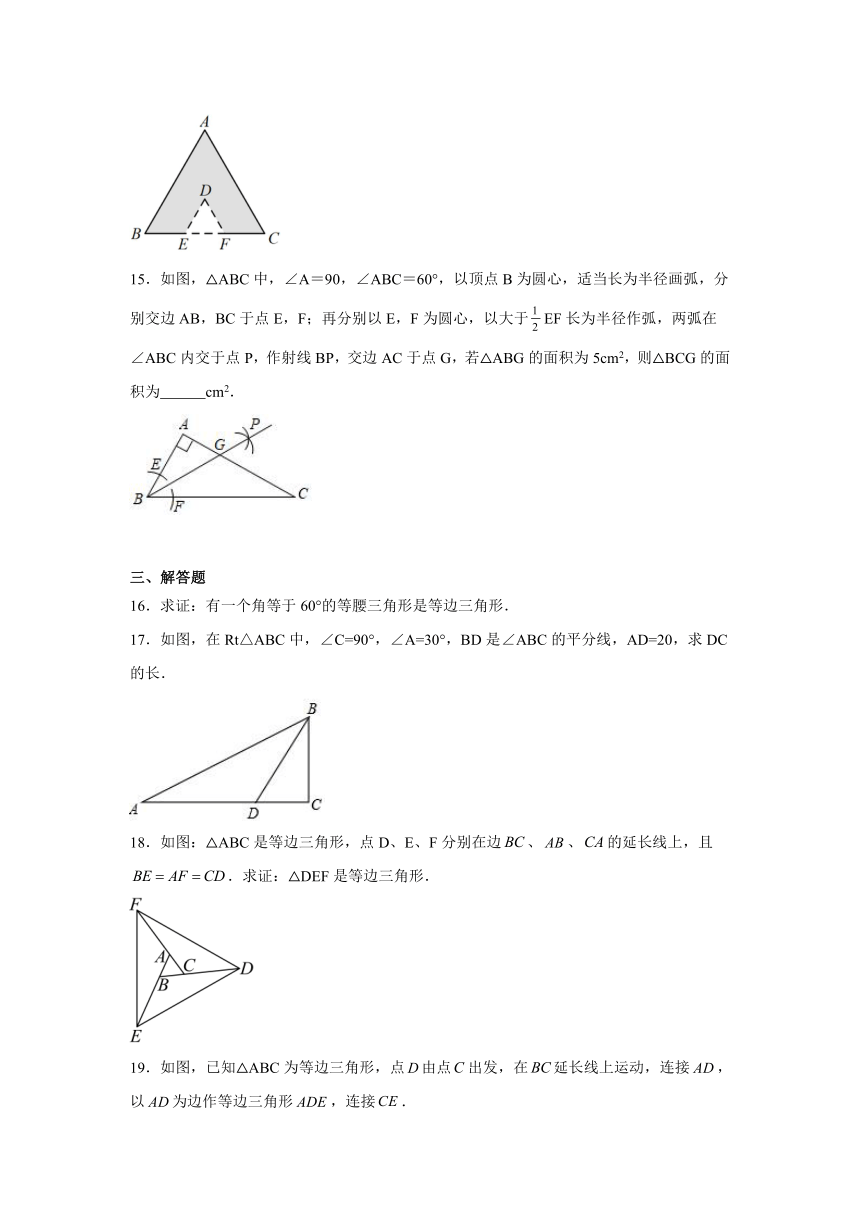
15.如图,△ABC中,∠A=90,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F;再分别以E,F为圆心,以大于EF长为半径作弧,两弧在∠ABC内交于点P,作射线BP,交边AC于点G,若△ABG的面积为5cm2,则△BCG的面积为 cm2.
三、解答题
16.求证:有一个角等于60°的等腰三角形是等边三角形.
17.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求DC的长.
18.如图:△ABC是等边三角形,点D、E、F分别在边、、的延长线上,且.求证:△DEF是等边三角形.
19.如图,已知△ABC为等边三角形,点由点出发,在延长线上运动,连接,以为边作等边三角形,连接.
(1)证明:;
(2)若,点的运动速度为每秒,运动时间为秒,则为何值时,?
20.(1)【操作发现】如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.线段AF与BD之间的数量关系是______.
(2)【类比猜想】如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?并加以证明;
(3)【深入探究】如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△,连接AF,,探究AF,与AB有何数量关系?并证明你的探究的结论.
参考答案:
1.B
2.B
3.D
4.B
5.B
6.C
7.D
8.D
9.D
10.B
11./
12.30°
13.4.
14.6
15.10
16.解:如图已知AB=AC.
①如果∠B=60°,那么∠C=∠B=60°.
所以∠A=180°﹣(∠B+∠C)=180°﹣(60°+60°):60°
于是∠A=∠B=∠C,所以△ABC是等边三角形.
②如果∠A=60°,
由∠A+∠B+∠C=180°和∠B=∠C得
∠B==(180°﹣60°)=60°.
于是∠B=∠C=∠A,所以△ABC是等边三角形.
综上所述,有一个角等于60°的等腰三角形是等边三角形.
17.10.
18.证明:∵△ABC是等边三角形,
∴,
∴,
∵,
∴,
∴△FAE与△EBD与△DCF全等
∴,
∴△DEF是等边三角形.
19.(1)证明:∵△ABC和△ADE均为等边三角形
∴AB=AC=BC,AD=AE,∠BAC=60°,∠DAE=60°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠BAD=∠CAE
在△BAD和△CAE中
∴△BAD≌△CAE(SAS)
∴CE=BD
又BD=BC+CD=AC+CD
∴CE=AC+CD
(2)解:如图所示
∵△ADE是等边三角形
若CE⊥AD
则CE是△ADE的边AD的垂直平分线
∴CD=CA=AB=6
∴t=6÷2=3(s)
20.(1);(2)成立;(3)
2023—2024学年人教版数学八年级上册
一、单选题
1.等边三角形是( ).
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰直角三角形
2.正三角形的边长为4,AD是BC边上的高,则BD是( ).
A.1 B.2 C.3 D.4
3.如图,直线,△ABC是等边三角形,若,则的度数为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,∠A=15°,AB的垂直平分线与AC交于点M,则BC与MB的比为( )
A.1:3 B.1:2 C.2:3 D.3:4
5.如图所示,已知△ABC是等边三角形,点是上任意一点,,分别于两边垂直,等边三角形的高为1,则的值为( )
A. B.1 C.2 D.不确定
6.如图,D是等边△ABC的边AC上的一点,E是等边△ABC外一点,若,
,则对△ADE的形状最准确的是( ).
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
7.如图,已知将△ABE沿所在直线翻折,点恰好与上的点重合,对折边,折痕也经过点,则下列说法正确的是( )
①;
②;
③;
④S△ACD:S △ACE= ;
⑤若,则△ABC是等边三角形.
A.只有①②正确 B.①②③
C.①②③④ D.①②③④⑤
8.如图,∠AOB=120°,OP平分∠AOB,且OP=2,若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
A.2个 B.3个 C.4个 D.无数个
9.已知如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下四个结论:①AD=BE;②△CPQ是等边三角形;③AD⊥BC;④OC平分∠AOE.其中正确的结论是( )
A.①②③④ B.③④ C.①②③ D.①②④
10.如图,两个全等的等边三角形的边长为1米,一个微型机器人由点开始按的顺序沿等边三角形的边循环运动,行走2023米停下,则这个微型机器人停在( )
A.点A处 B.点B处 C.点C处 D.点D处
二、填空题
11.等边三角形的周长为,则它的边长为 .
12.如图,△ABC为等边三角形,AD为BC边上的高,则∠BAD= .
13.如图所示,AD∥BC,BD平分∠ABC.若∠ABD=30°,∠BDC=90°,CD=2,则BC= .
14.如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是 .
15.如图,△ABC中,∠A=90,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F;再分别以E,F为圆心,以大于EF长为半径作弧,两弧在∠ABC内交于点P,作射线BP,交边AC于点G,若△ABG的面积为5cm2,则△BCG的面积为 cm2.
三、解答题
16.求证:有一个角等于60°的等腰三角形是等边三角形.
17.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求DC的长.
18.如图:△ABC是等边三角形,点D、E、F分别在边、、的延长线上,且.求证:△DEF是等边三角形.
19.如图,已知△ABC为等边三角形,点由点出发,在延长线上运动,连接,以为边作等边三角形,连接.
(1)证明:;
(2)若,点的运动速度为每秒,运动时间为秒,则为何值时,?
20.(1)【操作发现】如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.线段AF与BD之间的数量关系是______.
(2)【类比猜想】如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?并加以证明;
(3)【深入探究】如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△,连接AF,,探究AF,与AB有何数量关系?并证明你的探究的结论.
参考答案:
1.B
2.B
3.D
4.B
5.B
6.C
7.D
8.D
9.D
10.B
11./
12.30°
13.4.
14.6
15.10
16.解:如图已知AB=AC.
①如果∠B=60°,那么∠C=∠B=60°.
所以∠A=180°﹣(∠B+∠C)=180°﹣(60°+60°):60°
于是∠A=∠B=∠C,所以△ABC是等边三角形.
②如果∠A=60°,
由∠A+∠B+∠C=180°和∠B=∠C得
∠B==(180°﹣60°)=60°.
于是∠B=∠C=∠A,所以△ABC是等边三角形.
综上所述,有一个角等于60°的等腰三角形是等边三角形.
17.10.
18.证明:∵△ABC是等边三角形,
∴,
∴,
∵,
∴,
∴△FAE与△EBD与△DCF全等
∴,
∴△DEF是等边三角形.
19.(1)证明:∵△ABC和△ADE均为等边三角形
∴AB=AC=BC,AD=AE,∠BAC=60°,∠DAE=60°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠BAD=∠CAE
在△BAD和△CAE中
∴△BAD≌△CAE(SAS)
∴CE=BD
又BD=BC+CD=AC+CD
∴CE=AC+CD
(2)解:如图所示
∵△ADE是等边三角形
若CE⊥AD
则CE是△ADE的边AD的垂直平分线
∴CD=CA=AB=6
∴t=6÷2=3(s)
20.(1);(2)成立;(3)
