24.2 点和圆、直线和圆的位置关系 培优训练 (无答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系 培优训练 (无答案)2023-2024学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 751.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 20:43:53 | ||
图片预览


文档简介
24.2 点和圆、直线和圆的位置关系(培优训练)-人教版九年级上册
一.选择题
.如图,点P为⊙O外一点,PA为⊙O的切线,PO交⊙O于点B,∠P=30°,则线段OP的长为( )
A.3 B. C.6 D.9
.如图,AB是⊙O的直径,AC切⊙O于点A,连接OD,若∠C=70°( )
A.30° B.35° C.40° D.45°
.如图,△ABC内接于⊙O,过A点作直线DE( )时,直线DE与⊙O相切.
A.∠B B.∠BAC C.∠C D.∠DAC
.如图,在边长为1的正方形ABCD中,P是对角线AC上一点,PB,过点P作PE⊥PD,下列结论:①PB=PD;②PD=PE;④PE的最小值为.其中正确的是( )
A.①② B.①④ C.①②③ D.①②③④
.嘉嘉与淇淇在讨论下面的问题:如图,RtABC中,AB=60,∠BAC=90°.D,E
分别是AC,DE=52,以DE为直径的⊙O交BC于点P,求线段PQ的最大值.嘉嘉:当点D,E分别在AC,点O到点A的距离为定值;淇淇:当PQ为圆O的直径时,下列说法正确的是( )
A.两人的说法都正确,线段PQ的最大值为52
B.嘉嘉的说法正确,淇淇的说法有问题,线段PQ长度的最大值为48
C.淇淇的说法有问题,当DE∥BC时,线段PQ的长度最大
D.这道题目有问题,PQ的长度只有最小值,没有最大值
.如图,日晷是中国古代用来测定时间的仪器,利用与晷盘垂直的晷针投射到晷盘上的影子来测定时间.淄博市某学校内A处有一个日晷模型,平面示意图如下,A处的纬度为北纬36°48′(地球球心为O,A处的纬度是指OA与赤道面所成角)( )
A.36°48' B.53°12° C.53°52' D.90°
.如图,AB是⊙O的直径,点E,点A是的中点,交BC的延长线于点D,连接EC.若∠ADB=58.5°( )
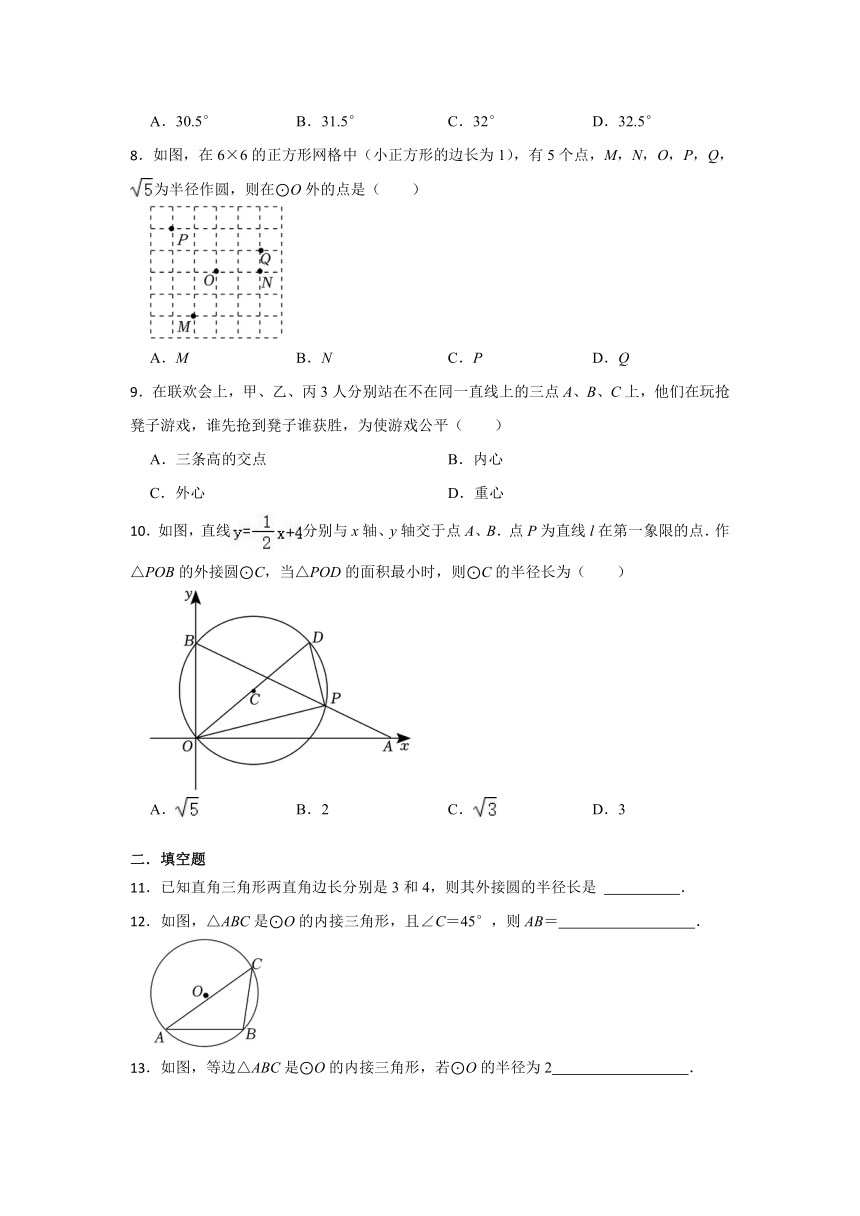
A.30.5° B.31.5° C.32° D.32.5°
.如图,在6×6的正方形网格中(小正方形的边长为1),有5个点,M,N,O,P,Q,为半径作圆,则在⊙O外的点是( )
A.M B.N C.P D.Q
.在联欢会上,甲、乙、丙3人分别站在不在同一直线上的三点A、B、C上,他们在玩抢凳子游戏,谁先抢到凳子谁获胜,为使游戏公平( )
A.三条高的交点 B.内心
C.外心 D.重心
.如图,直线分别与x轴、y轴交于点A、B.点P为直线l在第一象限的点.作△POB的外接圆⊙C,当△POD的面积最小时,则⊙C的半径长为( )
A. B.2 C. D.3
二.填空题
.已知直角三角形两直角边长分别是3和4,则其外接圆的半径长是 .
.如图,△ABC是⊙O的内接三角形,且∠C=45°,则AB= .
.如图,等边△ABC是⊙O的内接三角形,若⊙O的半径为2 .
.已知⊙O1的半径为1,⊙O2的半径为r,圆心距O1O2=5,如果在⊙O2上存在一点P,使得PO1=2,则r的取值范围是 .
.有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,∠ABC=90°,点M,BC上,MN长度始终保持不变.MN=4,点D到BA,BC的距离分别为3和2,猫与老鼠的距离DE的最小值为 .
三.解答题
.如图,已知△ABC是等边三角形,以AB为直径作⊙O,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为2,求EF的长度.
.如图,已知AB为⊙O的直径,弦CD⊥AB,连接AC、BD,点F为BD延长线上一点,且∠BAC=∠F.
(1)求证:AF为⊙O的切线;
(2)若⊙O的半径为4,点E为OA的中点,求AF的长.
.如图1,AB是⊙O的切线,切点为点B,点D是优弧BC上一点,连接BD
(1)求证∠A+2∠D=90°;
(2)如图2,若BD⊥OC,∠A=∠D,求AB的长.
.如图,AB是⊙O的直径,AC是弦,且CF=EF.
(1)求证:点D是弧AB的中点.
(2)连接BD,取BD的中点G,连接AG.若CF=8,求AG的长.
.如图,在△ABC,AB=AC,点F在AC的延长线上,且BF是⊙O的切线.
(1)求证:∠BAC=2∠CBF;
(2)若⊙O的半径为5,sin∠CBF=,求CD的长.
一.选择题
.如图,点P为⊙O外一点,PA为⊙O的切线,PO交⊙O于点B,∠P=30°,则线段OP的长为( )
A.3 B. C.6 D.9
.如图,AB是⊙O的直径,AC切⊙O于点A,连接OD,若∠C=70°( )
A.30° B.35° C.40° D.45°
.如图,△ABC内接于⊙O,过A点作直线DE( )时,直线DE与⊙O相切.
A.∠B B.∠BAC C.∠C D.∠DAC
.如图,在边长为1的正方形ABCD中,P是对角线AC上一点,PB,过点P作PE⊥PD,下列结论:①PB=PD;②PD=PE;④PE的最小值为.其中正确的是( )
A.①② B.①④ C.①②③ D.①②③④
.嘉嘉与淇淇在讨论下面的问题:如图,RtABC中,AB=60,∠BAC=90°.D,E
分别是AC,DE=52,以DE为直径的⊙O交BC于点P,求线段PQ的最大值.嘉嘉:当点D,E分别在AC,点O到点A的距离为定值;淇淇:当PQ为圆O的直径时,下列说法正确的是( )
A.两人的说法都正确,线段PQ的最大值为52
B.嘉嘉的说法正确,淇淇的说法有问题,线段PQ长度的最大值为48
C.淇淇的说法有问题,当DE∥BC时,线段PQ的长度最大
D.这道题目有问题,PQ的长度只有最小值,没有最大值
.如图,日晷是中国古代用来测定时间的仪器,利用与晷盘垂直的晷针投射到晷盘上的影子来测定时间.淄博市某学校内A处有一个日晷模型,平面示意图如下,A处的纬度为北纬36°48′(地球球心为O,A处的纬度是指OA与赤道面所成角)( )
A.36°48' B.53°12° C.53°52' D.90°
.如图,AB是⊙O的直径,点E,点A是的中点,交BC的延长线于点D,连接EC.若∠ADB=58.5°( )
A.30.5° B.31.5° C.32° D.32.5°
.如图,在6×6的正方形网格中(小正方形的边长为1),有5个点,M,N,O,P,Q,为半径作圆,则在⊙O外的点是( )
A.M B.N C.P D.Q
.在联欢会上,甲、乙、丙3人分别站在不在同一直线上的三点A、B、C上,他们在玩抢凳子游戏,谁先抢到凳子谁获胜,为使游戏公平( )
A.三条高的交点 B.内心
C.外心 D.重心
.如图,直线分别与x轴、y轴交于点A、B.点P为直线l在第一象限的点.作△POB的外接圆⊙C,当△POD的面积最小时,则⊙C的半径长为( )
A. B.2 C. D.3
二.填空题
.已知直角三角形两直角边长分别是3和4,则其外接圆的半径长是 .
.如图,△ABC是⊙O的内接三角形,且∠C=45°,则AB= .
.如图,等边△ABC是⊙O的内接三角形,若⊙O的半径为2 .
.已知⊙O1的半径为1,⊙O2的半径为r,圆心距O1O2=5,如果在⊙O2上存在一点P,使得PO1=2,则r的取值范围是 .
.有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,∠ABC=90°,点M,BC上,MN长度始终保持不变.MN=4,点D到BA,BC的距离分别为3和2,猫与老鼠的距离DE的最小值为 .
三.解答题
.如图,已知△ABC是等边三角形,以AB为直径作⊙O,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为2,求EF的长度.
.如图,已知AB为⊙O的直径,弦CD⊥AB,连接AC、BD,点F为BD延长线上一点,且∠BAC=∠F.
(1)求证:AF为⊙O的切线;
(2)若⊙O的半径为4,点E为OA的中点,求AF的长.
.如图1,AB是⊙O的切线,切点为点B,点D是优弧BC上一点,连接BD
(1)求证∠A+2∠D=90°;
(2)如图2,若BD⊥OC,∠A=∠D,求AB的长.
.如图,AB是⊙O的直径,AC是弦,且CF=EF.
(1)求证:点D是弧AB的中点.
(2)连接BD,取BD的中点G,连接AG.若CF=8,求AG的长.
.如图,在△ABC,AB=AC,点F在AC的延长线上,且BF是⊙O的切线.
(1)求证:∠BAC=2∠CBF;
(2)若⊙O的半径为5,sin∠CBF=,求CD的长.
同课章节目录
