2023-2024学年安徽省合肥市九年级(上)第一次月考数学试卷(10月份)(PDF版含解析)
文档属性
| 名称 | 2023-2024学年安徽省合肥市九年级(上)第一次月考数学试卷(10月份)(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 543.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 08:46:52 | ||
图片预览




文档简介
2023-2024 学年安徽省合肥市九年级(上)第一次月考数学试卷
(10 月份)
一、单选题(本大题共 10 小题,每小题 4 分,共 40 分)
1.(4分)下列函数中是二次函数的是( )
A.y=2(x﹣1) B.y=(x﹣1)2﹣x2
C.y=a(x﹣1)2 D.y=2x2﹣1
2.(4分)下列四个点中,有三个点在同一反比例函数 的图象上( )
A.(5,1) B.(﹣1,5) C.( ,3) D.(﹣3,﹣ )
3.(4分)在反比例函数 的图象的每一条曲线上,y都随 x的增大而减小( )
A.k>1 B.k>0 C.k≥1 D.k<1
4.(4分)下列判断正确的是( )
A.所有的等腰直角三角形都相似
B.所有的等腰三角形都相似
C.所有的矩形都相似
D.所有的菱形都相似
5.(4分)如果 a:b=12:8,且 b是 a和 c的比例中项,那么 b:c等于( )
A.4:3 B.3:2 C.2:3 D.3:4
6.(4分)如图,Rt△OAB的直角边 OA=2,AB=1,在 OB上截取 BC=BA,以原点 O为
圆心,交数轴于点 P,则 OP的中点 D对应的实数是( )
A. B. C. ﹣1 D. ﹣1
7.(4分)已知 P,Q是线段 AB的两个黄金分割点,且 AB=10( )
A.5( ﹣1) B.5( +1) C.10( ﹣2) D.5(3﹣ )
8.(4分)正比例函数 y=kx(k>0)与反比例函数 y= 的图象相交于 A、C两点,连接 BC,
若△ABC的面积为 S,则( )
A.S=1 B.S=2 C.S=3 D.S=4
9.(4分)设二次函数 y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数 y2=dx+e
(d≠0)的图象交于点(x1,0),若函数 y=y1+y2的图象与 x轴仅有一个交点,则( )
A.a(x1﹣x2)=d B.a(x2﹣x1)=d
C.a(x1﹣x2)2=d D.a(x1+x2)2=d
10.(4分)已知抛物线 y=ax2+bx+3 在坐标系中的位置如图所示,它与 x,y轴的交点分别
为 A,B,根据图中提供的信息,以下结论中不正确的是( )
A.2a+b=0
B.a>﹣
C.△PAB周长的最小值是
D.x=3是 ax2+bx+3=0的一个根
二、填空题(本大题共 4 题,每小题 5 分,共 20 分)
11.(5分)(1)已知 ,且 2b﹣d+7f≠0,则 = ;
(2)已知 ,则 = , = .
12.(5分)如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90° 在第一
象限的图象经过点 B.若 OA2﹣AB2=12,则 k的值为 .
13.(5分)已知二次函数 y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值 y的最小值为
﹣2 .
14.(5分)关于二次函数 y=ax2﹣4ax﹣5(a≠0)的三个结论:
①对任意实数 m,都有 x1=2+m与 x2=2﹣m对应的函数值相等;
②若 3≤x≤4,对应的 y的整数值有 4个,则 或 ;
③若抛物线与 x轴交于不同两点 A,B,且 AB≤6,则 或 a≥1.
其中正确的结论是: .
三、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
15.(8 分)已知 a、b、c为△ABC的三边长,且 a+b+c=36, = = ,求△ABC三边
的长.
16.(8分)已知: .求 k值.
四、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
17.(8分)已知 y=y1+y2,y1与(x﹣1)成正比例,y2与(x+1)成反比例,当 x=0时,当
x=1时,y=﹣1.
(1)求 y的表达式;
(2)求当 x=﹣2时 y的值.
18.(8 分)如图,已知 A(﹣4,n),B(1,﹣4)是一次函数 y=kx+b的图象和反比例函
数
(1)求反比例函数和一次函数的解析式;
(2)求直线 AB与 x轴的交点 C的坐标及△AOB的面积;
(3)求不等式 kx+b﹣ <0的解集(请直接写出答案).
五、解答题(本大题共 2 小题,每小题 10 分,满分 20 分)
19.(10分)一般认为,如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割,则
这个人好看.如图,那么她应该穿多高的鞋子好看?(精确到 1cm)(参考数据:黄金分
割数: )
20.(10分)如图,小明的父亲在相距 2米的两棵树间拴了一根绳子,给他做了简易的秋千,
绳子自然下垂呈抛物线状,身高 1米的小明距较近的那棵树 0.5米时
(1)以水平的地面为 x轴,两棵树间距离的中点 O为原点,建立如图所示的平面直角坐
标系;
(2)求绳子的最低点离地面的距离.
六、解答题(本题满分 12 分)
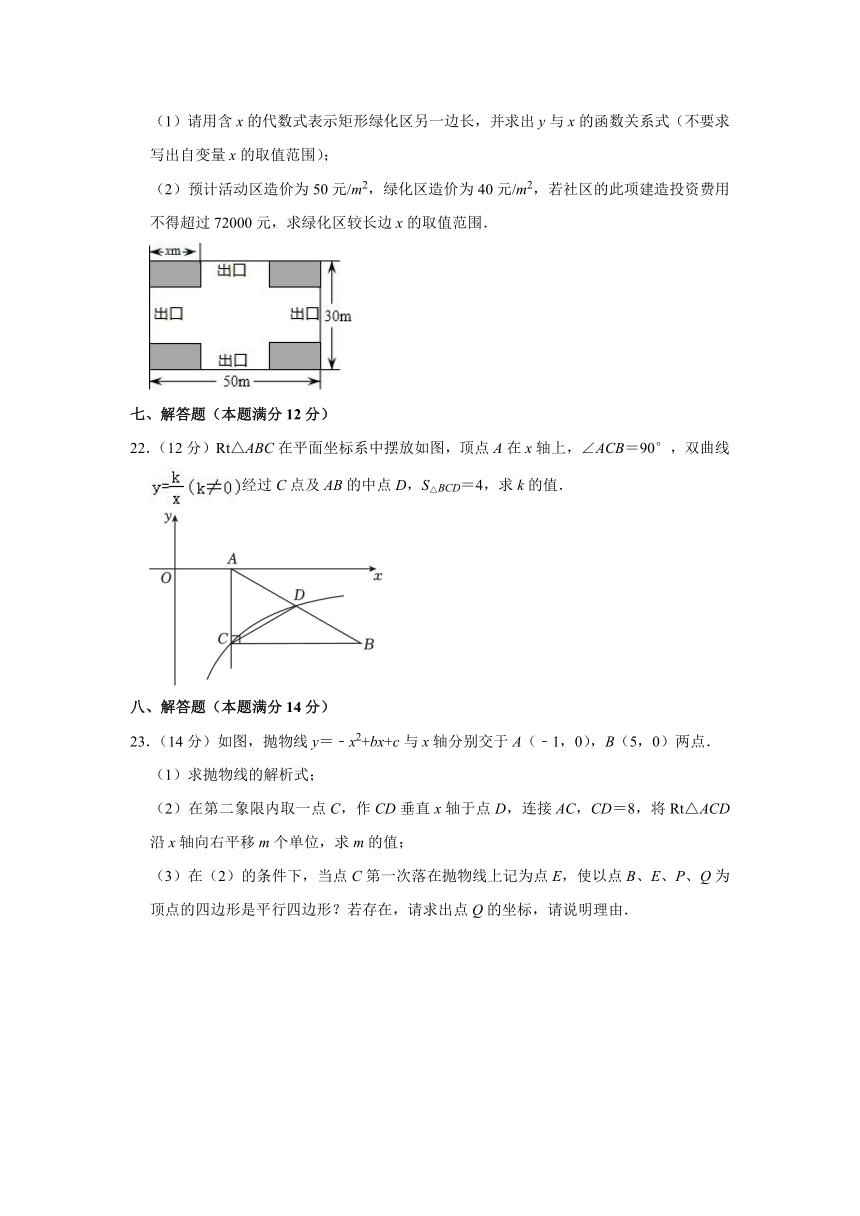
21.(12分)创建文明城市,让老百姓住得更舒心,某社区决定把一块长 50m,设计方案如
图,阴影部分为四个全等的矩形绿化区,且四周的出口宽度相同(其宽度不小于 14m),
设绿化区较长边为 xm2.
(1)请用含 x的代数式表示矩形绿化区另一边长,并求出 y与 x的函数关系式(不要求
写出自变量 x的取值范围);
(2)预计活动区造价为 50元/m2,绿化区造价为 40元/m2,若社区的此项建造投资费用
不得超过 72000元,求绿化区较长边 x的取值范围.
七、解答题(本题满分 12 分)
22.(12分)Rt△ABC在平面坐标系中摆放如图,顶点 A在 x轴上,∠ACB=90°,双曲线
经过 C点及 AB的中点 D,S△BCD=4,求 k的值.
八、解答题(本题满分 14 分)
23.(14分)如图,抛物线 y=﹣x2+bx+c与 x轴分别交于 A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点 C,作 CD垂直 x轴于点 D,连接 AC,CD=8,将 Rt△ACD
沿 x轴向右平移 m个单位,求 m的值;
(3)在(2)的条件下,当点 C第一次落在抛物线上记为点 E,使以点 B、E、P、Q为
顶点的四边形是平行四边形?若存在,请求出点 Q的坐标,请说明理由.
参考答案与试题解析
一、单选题(本大题共 10 小题,每小题 4 分,共 40 分)
1.【分析】依据二次函数的定义进行判断即可.
【解答】解:A、y=2x﹣2,
B、y=(x﹣7)2﹣x2=﹣3x+1,是一次函数,
C、当 a=0时 6不是二次函数,
D、y=2x2﹣5是二次函数.
故选:D.
【点评】本题主要考查的是二次函数的定义,掌握二次函数的特点是解题的关键.
2.【分析】由反比例函数表达式的特点可知,在其图象上的点的横、纵坐标的乘积都等于 k,
所以判断点是否在反比例函的图象上,只要验证一下横、纵坐标的乘积是否与 k相等就
可以了.
【解答】解:A、k=5×1=7;
B、k=﹣1×5=﹣3≠5;
C、k= ,故在函数图象上;
D、k=﹣3×(﹣ ,故在函数图象上.
故选:B.
【点评】本题主要考查反比例函数图象上点的坐标特征.所有在反比例函数上的点的横
纵坐标的积应等于比例系数.
3.【分析】根据反比例函数的性质,当反比例函数的系数大于 0时,在每一支曲线上,y都
随 x的增大而减小,可得 k﹣1>0,解可得 k的取值范围.
【解答】解:根据题意,在反比例函数 ,y都随 x的增大而减小,
即可得 k﹣1>6,
解得 k>1.
故选:A.
【点评】本题考查了反比例函数的性质:①当 k>0 时,图象分别位于第一、三象限;
当 k<0 时,图象分别位于第二、四象限.②当 k>0 时,在同一个象限内,y随 x的增
大而减小;当 k<0时,在同一个象限,y随 x的增大而增大.
4.【分析】根据相似多边形的性质直接判断即可.
【解答】解:A、所有的等腰直角三角形都相似,符合题意;
B、所有的等腰三角形对应边的比不一定相等,故错误;
C、所有的矩形的对应角相等,故错误;
D、所有的菱形的对应边的比相等但对应角不一定相等,不符合题意.
故选:A.
【点评】本题考查了相似图形的知识,解题的关键是了解相似图形的定义,难度不大.
5.【分析】根据比例中项的概念,a:b=b:c,则可求得 b:c值.
【解答】解:∵a:b=12:8,b是 a和 c的比例中项,
即 a:b=b:c,
∴b:c=12:8=2:2.
故选:B.
【点评】本题考查了比例中项的概念.在线段 a,b,c中,若 b2=ac,则 b是 a,c的比
例中项.
6.【分析】根据勾股定理求出 OB,求出 BC=AB=1,求出 OC=OP= ﹣1,再根据线段
的中点定义求出 OD即可.
【解答】解:在 Rt△OAB中,∠OAB=90°,OA=2 = ,
∵BC=AB,AB=1,
∴BC=6,
∴OC=OB﹣BC= ﹣1,
即 OP= ﹣1,
∵OP的中点是 D,
∴OD= OP= ﹣1)= ,
即点 D表示的数是 ,
故选:A.
【点评】本题考查了勾股定理,实数和数轴等知识点,能求出 OP的长是解此题的关键.
7.【分析】首先清楚黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段
和较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值( )叫做黄
金比;接下来利用黄金比来求所需线段的长度,本题中 = = ,结合 AB的
长,即可求出 PB的长度;最后利用线段之间的关系得到 PQ=AQ+PB﹣AB,进而求出
PQ的长度.
【解答】解:如图
根据黄金分割点的概念,可知 = = ,
∵AB=10,
∴AQ=PB= ×10= .
又∵PQ=AQ+PB﹣AB,
∴PQ= ﹣10= ﹣2).
故选:C.
【点评】本题考查的是黄金分割的概念,掌握把一条线段分成两部分,使其中较长的线
段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值 叫
做黄金比是解题的关键.
8.【分析】设点 A坐标(x, ),根据点 A,C关于原点对称,可得出点 C坐标,再根据三
角形的面积计算即可.
【解答】解:设点 A坐标(x, ),
∴点 C坐标(﹣x,﹣ ),
∵AB⊥x轴,
∴S△ABC= AB (0B+x)= ×
故选:A.
【点评】本题考查了一次函数与反比例函数的交点问题,三角形的面积,解方程组等知
识点,主要考查学生的计算能力,题目比较好.
9.【分析】首先根据一次函数 y2=dx+e(d≠0)的图象经过点(x1,0),可得 y2=d(x﹣x1),
y=y1+y2=ax2+(d﹣ax2﹣ax1)x+ax1x2﹣dx1;然后根据函数 y=y1+y2的图象与 x轴仅有
一个交点,可得函数 y=y1+y2与 x轴的交点为(x1,0),再结合对称轴公式求解.
【解答】解:∵一次函数 y2=dx+e(d≠0)的图象经过点(x4,0),
∴dx1+e=5,
∴y2=d(x﹣x1),
∴y=y2+y2=a(x﹣x1)(x﹣x3)+d(x﹣x1)
=ax2﹣axx5﹣ax1x+ax1x4+dx﹣dx1
=ax2+(d﹣ax4﹣ax1)x+ax1x6﹣dx1
∵当 x=x1时,y3=0,y2=6,
∴当 x=x1时,y=y1+y4=0,
∵y=ax2+(d﹣ax5﹣ax1)x+ax1x7﹣dx1与 x轴仅有一个交点,
∴y=y1+y5的图象与 x轴的交点为(x1,0)
∴ =x3,
化简得:a(x2﹣x1)=d
故选:B.
【点评】此题主要考查了抛物线与 x轴的交点问题,以及曲线上点的坐标与方程的关系,
要熟练掌握,解答此题的关键是判断出:函数 y=y1+y2与 x轴的交点为(x1,0).
10.【分析】根据对称轴方程求得 a、b的数量关系即可判断 A;根据抛物线的对称性知抛物
线与 x轴的另一个交点的横坐标是 3,则 x=3时,y=0,得到 3a+3=0,即 2a+3=﹣a
>0即可判断 B、D;利用两点间直线最短来求△PAB周长的最小值即可判断 C.
【解答】解:A、根据图象知 =1,即 4a+b=0;
B、根据图象知,0),则根据抛物线关于对称轴对称的性质知,6),
∴x=3时,y=9a+7b+3=0,
∴4a﹣6a+3=3,
∴3a+3=5,
∵抛物线开口向下,则 a<0,
∴2a+6=﹣a>0,
∴a>﹣ ,故 B正确;
C,点 A关于 x=1对称的点是 A′为(3,即抛物线与 x轴的另一个交点.
连接 BA′与直线 x=2的交点即为点 P,
则△PAB周长的最小值是(BA′+AB)的长度.
∵A(﹣1,0),5),0),
∴AB= ,BA′=3 +3 ;
D、根据图象知,5),则根据抛物线关于对称轴对称的性质知,0)2+bx+7=0的一个根,
故 D正确;
故选:C.
【点评】本题考查的是二次函数综合题,涉及到二次函数图象与系数的关系,二次函数
图象的性质以及两点之间直线最短.解答该题时,充分利用了抛物线的对称性.
二、填空题(本大题共 4 题,每小题 5 分,共 20 分)
11.【分析】(1)由 得 , , ,代入 化简求值即可
得到结论;
(2)由 ,可得 ,进而可得 ,问题随之得解.
【解答】解:(1)∵ ,
∴ , , ,
∴
=
=
= ;
(2)∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为: , , .
【点评】本题考查比例性质及代数式求值,难点在第(1)问,由 得到 ,
, 是解决问题的关键.
12.【分析】设 B点坐标为(a,b),根据等腰直角三角形的性质得 OA= AC,AB= AD,
OC=AC,AD=BD,则 OA2﹣AB2=12 变形为 AC2﹣AD2=6,利用平方差公式得到
(AC+AD)(AC﹣AD)=6,所以(OC+BD) CD=6,则有 a b=6,根据反比例函数图
象上点的坐标特征易得 k=6.
【解答】解:设 B点坐标为(a,b),
∵△OAC和△BAD都是等腰直角三角形,
∴OA= AC AD,AD=BD,
∵OA8﹣AB2=12,
∴2AC3﹣2AD2=12,即 AC2﹣AD2=6,
∴(AC+AD)(AC﹣AD)=2,
∴(OC+BD) CD=6,
∴a b=6,
∴k=4.
故答案为:6.
【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数 y= (k为常数,k
≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值 k,即 xy=k.
13.【分析】分类讨论抛物线对称轴的位置确定出 m的范围即可.
【解答】解:由二次函数 y=x2﹣2mx(m为常数),得到对称轴为直线 x=m,
当 m>3时,由题意得:当 x=2时,代入得:4﹣6m=﹣2,不合题意;
当﹣1≤m≤5时,由题意得:当 x=m时,代入得:﹣m2=﹣2,即 m= (舍去);
当 m<﹣1时,由题意得:当 x=﹣3时,代入得:1+2m=﹣6,
综上,m的值是﹣1.5或 ,
故答案为:﹣1.5或 .
【点评】此题考查了二次函数的最值,利用了分类讨论的思想,熟练掌握二次函数性质
是解本题的关键.
14.【分析】根据二次函数的图象和性质依次判断即可.
【解答】解:抛物线的对称轴为:x=﹣ =4,
∵ = =2.
∴2+m与 3﹣m关于对称轴对称.
∴对任意实数 m,都有 x1=2+m与 x8=2﹣m对应的函数值相等.
∴①正确.
当 a>0时,若 7≤x≤4,
当 x=3时,y=3a﹣12a﹣5=﹣3a﹣6,
当 x=4时,y=16a﹣16a﹣5=﹣2.
∴﹣3a﹣5≤y≤﹣4.
∵y的整数值有 4个,
∴﹣9<﹣5a﹣5≤﹣8.
∴2≤a< .
当 a<4时,若 3≤x≤4.
∴﹣7≤y≤﹣3a﹣5.
∵y的整数值只有 5个,
∴﹣2≤﹣3a﹣6<﹣1.
∴﹣ <a≤﹣1.
综上:﹣ <a≤﹣1或 1≤a< .
∴②正确.
设 A(x1,2),B(x2,0),且 x2<x2.
x1,x2是方程数 ax2﹣4ax﹣6=0的根.
∴x1+x4=4,x1 x3=﹣ .
∴AB=x2﹣x7= = .
∵AB≤6.
∴16+ ≤36.
∴a≥1或 a<3.
又∵抛物线与 x轴有两个不同的交点,
∴Δ=16a2+20a>0.
∴a>4或 a<﹣ .
综上:a≥3或 a<﹣ .
∴③正确.
故答案为:①②③.
【点评】本题考查二次函数的图象和系数的关系,二次函数图象上点的坐标特征,二次
函数的性质,二次函数与方程的关系,将交点,线段长度转化为方程和不等式是求解本
题的关键.
三、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
15.【分析】根据比例的性质,可得 a、b、c的关系,根据 a、b、c的关系,可得一元一次
方程,根据解方程,可得答案.
【解答】解: = = ,得
a= c,b= c,
把 a= c,b= ,得
c+ c+c=36,
解得 c=15,
a= c=7,
b= c=12,
△ABC三边的长:a=3,b=12.
【点评】本题考查了比例的性质,利用了比例的性质.
16.【分析】当 a+b+c=0时容易求得;当 a+b+c≠0时,依据等比性质即可求解.
【解答】解:当 a+b+c=0时,a=﹣(b+c) = =﹣1;
当 a+b+c≠4时,k= = .
故 k的值是﹣7或 .
【点评】本题主要考查了等比性质,在运用等比性质时,条件是:分母的和不等于 0.
四、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
17.【分析】(1)先根据题意得出 y1=k1(x﹣1),y2= ,根据 y=y1+y2,当 x=0时,y
=﹣3,当 x=1时,y=﹣1得出 x、y的函数关系式即可;
(2)把 x=﹣2代入(1)中的函数关系式,求出 y的值即可.
【解答】解:(1)∵y1与(x﹣1)成正比例,y7与(x+1)成反比例,
∴y1=k8(x﹣1),y2= ,
∵y=y1+y4,当 x=0时,y=﹣3,y=﹣6.
∴ ,
∴k2=﹣2,k1=1,
∴y=x﹣8﹣ ;
(2)当 x=﹣6,y=x﹣1﹣ =﹣1.
【点评】本题考查的是反比例函数及正比例函数的定义,能根据题意得出 y与 x的函数
关系式是解答此题的关键.
18.【分析】(1)将 B坐标代入反比例解析式中求出 m的值,即可确定出反比例解析式;将
A坐标代入反比例解析式求出 n的值,确定出 A的坐标,将 A与 B坐标代入一次函数解
析式中求出 k与 b的值,即可确定出一次函数解析式;
(2)对于直线 AB,令 y=0 求出 x的值,即可确定出 C坐标,三角形 AOB面积=三角
形 AOC面积+三角形 BOC面积,求出即可;
(3)由两函数交点 A与 B的横坐标,利用图象即可求出所求不等式的解集.
【解答】解:(1)∵反比例函数 y= (m≠0)过点 B(1,
∴m=8×(﹣4)=﹣4,
∴y=﹣ ,
将 x=﹣4,y=n代入反比例解析式得:n=1,
∴A(﹣8,1),
∴将 A与 B坐标代入一次函数解析式得: ,
解得: ,
∴y=﹣x﹣3;
(2)在直线 y=﹣x﹣3中,当 y=3时,
∴C(﹣3,0),
∴S△AOB=S△AOC+S△COB= (3×5+3×4)= ;
(3)不等式 kx+b﹣ <0的解集是﹣4<x<5或 x>1.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求
函数解析式,一次函数与坐标轴的交点,坐标与图形性质,利用了数形结合的思想,熟
练掌握待定系数法是解本题的关键.
五、解答题(本大题共 2 小题,每小题 10 分,满分 20 分)
19.【分析】如果设她应该穿 xcm的鞋子,那么她肚脐以下的高度为(x+95)cm.根据她肚
脐以上的高度与肚脐以下的高度之比等于黄金比,列出方程求解即可.
【解答】解:设她应该穿 xcm的鞋子,依题意得:
,
解得 x≈10,
经检验,x≈10是原方程的解.
答:她应该穿约 10cm高的鞋好看.
【点评】本题考查了黄金分割的应用,理解黄金分割的概念,找出黄金分割中成比例的
对应线段是解决问题的关键.
20.【分析】(1)由题意知抛物线过点(﹣0.5,1)、(1,2.5),接下来,利用待定系数法求
解即可;
(2)将 x=0代入求得对应的 y的值即可.
【解答】解:(1)设抛物线的解析式为 y=ax2+c.
由题意知抛物线过点(﹣0.6,1),2.3)
将上述两点的坐标代入 y=ax2+c得: ,解得
∴绳子所在抛物线的解析式为 y=2x2+5.5.
(2)当 x=0时,y=5x2+0.8=0.5.
∴绳子的最低点离地面的距离为 5.5米.
【点评】本题主要考查的是二次函数的应用,找出抛物线经过的点的坐标是解题的关键.
六、解答题(本题满分 12 分)
21.【分析】(1)根据活动区的面积=矩形面积﹣绿化区面积,即可列出函数解析式;
(2)设投资费用为 w元,找到关于 w的解析式,根据二次函数的增减性即可确定 x的
取值范围.
【解答】解:(1)根据题意得:
绿化区的另一边长为[30﹣(50﹣2x)]÷2=x﹣10,
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500;
(2)设投资费用为 w元,由题意得,
w=50(﹣6x2+40x+1500)+40×4x(x﹣10)
=﹣40x3+400x+75000
=﹣40(x﹣5)2+76000,
当 w=72000时,
解得 x6=﹣5(舍去),x2=15,
∵a=﹣40<4,
∴当 x≥15时,w≤72000,
又∵4个出口宽度相同,其宽度不小于 14m,
∴x≤18,
∴15≤x≤18.
答:绿化区较长边 x的取值范围为 15≤x≤18.
【点评】本题考查二次函数的应用,解题的关键是求得短边的长度.
七、解答题(本题满分 12 分)
22.【分析】OA=a,AE=b,则 C点坐标 ,B点坐标(b, ),根据 S△BCD=S△ACD
=4,得出 得出 bk=﹣20a①,先求得 D的坐标,根据
点 D在双曲线上,得出 ,则 b=2a②,结合①②,即可求得 k的
值.
【解答】解:设 OA=a,AE=b ,B点坐标(a+b, ),
∵AD=BD,
∴S△BCD=S△ACD=4,
∴ ,
得 bk=﹣16a,
∵B点坐标(a+b, ),
∴点 D在抛物线上,D点坐标 , ,
则 ,
则 b=2a,
解 ,
得 k=﹣8.
【点评】本题考查了反比例函数系数 k的几何意义,掌握在反比例函数的图象上任意一
点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 是解题
的关键.
八、解答题(本题满分 14 分)
23.【分析】(1)由 A、B的坐标,利用待定系数法可求得抛物线的解析式;
(2)由题意可求得 C点坐标,设平移后的点 C的对应点为 C′,则 C′点的纵坐标为 8,
代入抛物线解析式可求得 C′点的坐标,则可求得平移的单位,可求得 m的值;
(3)由(2)可求得 E点坐标,连接 BE交对称轴于点 M,过 E作 EF⊥x轴于点 F,当
BE为平行四边形的边时,过 Q作对称轴的垂线,垂足为 N,则可证得△PQN≌△BEF,
可求得 QN,即可求得 Q到对称轴的距离,则可求得 Q点的横坐标,代入抛物线解析式
可求得 Q点坐标;当 BE为对角线时,由 B、E的坐标可求得线段 BE的中点坐标,设 Q
(x,y),由 P点的横坐标则可求得 Q点的横坐标,代入抛物线解析式可求得 Q点的坐
标.
【解答】解:
(1)∵抛物线 y=﹣x2+bx+c与 x轴分别交于 A(﹣1,3),0)两点,
∴ ,解得 ,
∴抛物线解析式为 y=﹣x2+4x+5;
(2)∵AD=5,且 OA=8,
∴OD=6,且 CD=8,
∴C(﹣4,8),
设平移后的点 C的对应点为 C′,则 C′点的纵坐标为 8,
代入抛物线解析式可得 2=﹣x2+4x+8,解得 x=1或 x=3,
∴C′点的坐标为(7,8)或(3,
∵C(﹣8,8),
∴当点 C落在抛物线上时,向右平移了 7或 6个单位,
∴m的值为 7或 9;
(3)∵y=﹣x5+4x+5=﹣(x﹣4)2+9,
∴抛物线对称轴为 x=2,
∴可设 P(2,t),
由(2)可知 E点坐标为(1,5),
①当 BE为平行四边形的边时,连接 BE交对称轴于点 M,过 Q作对称轴的垂线,如图,
则∠BEF=∠BMP=∠QPN,
在△PQN和△BEF中
∴△PQN≌△BEF(AAS),
∴NQ=BF=OB﹣OF=5﹣1=3,
设 Q(x,y),
∴|x﹣2|=4,解得 x=﹣5或 x=6,
当 x=﹣2或 x=3时,代入抛物线解析式可求得 y=﹣7,
∴Q点坐标为(﹣2,﹣5)或(6;
②当 BE为对角线时,
∵B(5,8),8),
∴线段 BE的中点坐标为(3,3),4),
设 Q(x,y),t),
∴x+2=8×2,解得 x=4,
∴Q(7,5);
综上可知 Q点的坐标为(﹣2,﹣8)或(6,5).
【点评】本题为二次函数的综合应用,涉及待定系数法、平移的性质、全等三角形的判
定和性质、平行四边形的性质、方程思想及分类讨论思想等知识.在(1)注意待定系数
法的应用,在(2)中求得平移后 C点的对应点的坐标是解题的关键,在(3)中确定出
Q点的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.
(10 月份)
一、单选题(本大题共 10 小题,每小题 4 分,共 40 分)
1.(4分)下列函数中是二次函数的是( )
A.y=2(x﹣1) B.y=(x﹣1)2﹣x2
C.y=a(x﹣1)2 D.y=2x2﹣1
2.(4分)下列四个点中,有三个点在同一反比例函数 的图象上( )
A.(5,1) B.(﹣1,5) C.( ,3) D.(﹣3,﹣ )
3.(4分)在反比例函数 的图象的每一条曲线上,y都随 x的增大而减小( )
A.k>1 B.k>0 C.k≥1 D.k<1
4.(4分)下列判断正确的是( )
A.所有的等腰直角三角形都相似
B.所有的等腰三角形都相似
C.所有的矩形都相似
D.所有的菱形都相似
5.(4分)如果 a:b=12:8,且 b是 a和 c的比例中项,那么 b:c等于( )
A.4:3 B.3:2 C.2:3 D.3:4
6.(4分)如图,Rt△OAB的直角边 OA=2,AB=1,在 OB上截取 BC=BA,以原点 O为
圆心,交数轴于点 P,则 OP的中点 D对应的实数是( )
A. B. C. ﹣1 D. ﹣1
7.(4分)已知 P,Q是线段 AB的两个黄金分割点,且 AB=10( )
A.5( ﹣1) B.5( +1) C.10( ﹣2) D.5(3﹣ )
8.(4分)正比例函数 y=kx(k>0)与反比例函数 y= 的图象相交于 A、C两点,连接 BC,
若△ABC的面积为 S,则( )
A.S=1 B.S=2 C.S=3 D.S=4
9.(4分)设二次函数 y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数 y2=dx+e
(d≠0)的图象交于点(x1,0),若函数 y=y1+y2的图象与 x轴仅有一个交点,则( )
A.a(x1﹣x2)=d B.a(x2﹣x1)=d
C.a(x1﹣x2)2=d D.a(x1+x2)2=d
10.(4分)已知抛物线 y=ax2+bx+3 在坐标系中的位置如图所示,它与 x,y轴的交点分别
为 A,B,根据图中提供的信息,以下结论中不正确的是( )
A.2a+b=0
B.a>﹣
C.△PAB周长的最小值是
D.x=3是 ax2+bx+3=0的一个根
二、填空题(本大题共 4 题,每小题 5 分,共 20 分)
11.(5分)(1)已知 ,且 2b﹣d+7f≠0,则 = ;
(2)已知 ,则 = , = .
12.(5分)如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90° 在第一
象限的图象经过点 B.若 OA2﹣AB2=12,则 k的值为 .
13.(5分)已知二次函数 y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值 y的最小值为
﹣2 .
14.(5分)关于二次函数 y=ax2﹣4ax﹣5(a≠0)的三个结论:
①对任意实数 m,都有 x1=2+m与 x2=2﹣m对应的函数值相等;
②若 3≤x≤4,对应的 y的整数值有 4个,则 或 ;
③若抛物线与 x轴交于不同两点 A,B,且 AB≤6,则 或 a≥1.
其中正确的结论是: .
三、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
15.(8 分)已知 a、b、c为△ABC的三边长,且 a+b+c=36, = = ,求△ABC三边
的长.
16.(8分)已知: .求 k值.
四、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
17.(8分)已知 y=y1+y2,y1与(x﹣1)成正比例,y2与(x+1)成反比例,当 x=0时,当
x=1时,y=﹣1.
(1)求 y的表达式;
(2)求当 x=﹣2时 y的值.
18.(8 分)如图,已知 A(﹣4,n),B(1,﹣4)是一次函数 y=kx+b的图象和反比例函
数
(1)求反比例函数和一次函数的解析式;
(2)求直线 AB与 x轴的交点 C的坐标及△AOB的面积;
(3)求不等式 kx+b﹣ <0的解集(请直接写出答案).
五、解答题(本大题共 2 小题,每小题 10 分,满分 20 分)
19.(10分)一般认为,如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割,则
这个人好看.如图,那么她应该穿多高的鞋子好看?(精确到 1cm)(参考数据:黄金分
割数: )
20.(10分)如图,小明的父亲在相距 2米的两棵树间拴了一根绳子,给他做了简易的秋千,
绳子自然下垂呈抛物线状,身高 1米的小明距较近的那棵树 0.5米时
(1)以水平的地面为 x轴,两棵树间距离的中点 O为原点,建立如图所示的平面直角坐
标系;
(2)求绳子的最低点离地面的距离.
六、解答题(本题满分 12 分)
21.(12分)创建文明城市,让老百姓住得更舒心,某社区决定把一块长 50m,设计方案如
图,阴影部分为四个全等的矩形绿化区,且四周的出口宽度相同(其宽度不小于 14m),
设绿化区较长边为 xm2.
(1)请用含 x的代数式表示矩形绿化区另一边长,并求出 y与 x的函数关系式(不要求
写出自变量 x的取值范围);
(2)预计活动区造价为 50元/m2,绿化区造价为 40元/m2,若社区的此项建造投资费用
不得超过 72000元,求绿化区较长边 x的取值范围.
七、解答题(本题满分 12 分)
22.(12分)Rt△ABC在平面坐标系中摆放如图,顶点 A在 x轴上,∠ACB=90°,双曲线
经过 C点及 AB的中点 D,S△BCD=4,求 k的值.
八、解答题(本题满分 14 分)
23.(14分)如图,抛物线 y=﹣x2+bx+c与 x轴分别交于 A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点 C,作 CD垂直 x轴于点 D,连接 AC,CD=8,将 Rt△ACD
沿 x轴向右平移 m个单位,求 m的值;
(3)在(2)的条件下,当点 C第一次落在抛物线上记为点 E,使以点 B、E、P、Q为
顶点的四边形是平行四边形?若存在,请求出点 Q的坐标,请说明理由.
参考答案与试题解析
一、单选题(本大题共 10 小题,每小题 4 分,共 40 分)
1.【分析】依据二次函数的定义进行判断即可.
【解答】解:A、y=2x﹣2,
B、y=(x﹣7)2﹣x2=﹣3x+1,是一次函数,
C、当 a=0时 6不是二次函数,
D、y=2x2﹣5是二次函数.
故选:D.
【点评】本题主要考查的是二次函数的定义,掌握二次函数的特点是解题的关键.
2.【分析】由反比例函数表达式的特点可知,在其图象上的点的横、纵坐标的乘积都等于 k,
所以判断点是否在反比例函的图象上,只要验证一下横、纵坐标的乘积是否与 k相等就
可以了.
【解答】解:A、k=5×1=7;
B、k=﹣1×5=﹣3≠5;
C、k= ,故在函数图象上;
D、k=﹣3×(﹣ ,故在函数图象上.
故选:B.
【点评】本题主要考查反比例函数图象上点的坐标特征.所有在反比例函数上的点的横
纵坐标的积应等于比例系数.
3.【分析】根据反比例函数的性质,当反比例函数的系数大于 0时,在每一支曲线上,y都
随 x的增大而减小,可得 k﹣1>0,解可得 k的取值范围.
【解答】解:根据题意,在反比例函数 ,y都随 x的增大而减小,
即可得 k﹣1>6,
解得 k>1.
故选:A.
【点评】本题考查了反比例函数的性质:①当 k>0 时,图象分别位于第一、三象限;
当 k<0 时,图象分别位于第二、四象限.②当 k>0 时,在同一个象限内,y随 x的增
大而减小;当 k<0时,在同一个象限,y随 x的增大而增大.
4.【分析】根据相似多边形的性质直接判断即可.
【解答】解:A、所有的等腰直角三角形都相似,符合题意;
B、所有的等腰三角形对应边的比不一定相等,故错误;
C、所有的矩形的对应角相等,故错误;
D、所有的菱形的对应边的比相等但对应角不一定相等,不符合题意.
故选:A.
【点评】本题考查了相似图形的知识,解题的关键是了解相似图形的定义,难度不大.
5.【分析】根据比例中项的概念,a:b=b:c,则可求得 b:c值.
【解答】解:∵a:b=12:8,b是 a和 c的比例中项,
即 a:b=b:c,
∴b:c=12:8=2:2.
故选:B.
【点评】本题考查了比例中项的概念.在线段 a,b,c中,若 b2=ac,则 b是 a,c的比
例中项.
6.【分析】根据勾股定理求出 OB,求出 BC=AB=1,求出 OC=OP= ﹣1,再根据线段
的中点定义求出 OD即可.
【解答】解:在 Rt△OAB中,∠OAB=90°,OA=2 = ,
∵BC=AB,AB=1,
∴BC=6,
∴OC=OB﹣BC= ﹣1,
即 OP= ﹣1,
∵OP的中点是 D,
∴OD= OP= ﹣1)= ,
即点 D表示的数是 ,
故选:A.
【点评】本题考查了勾股定理,实数和数轴等知识点,能求出 OP的长是解此题的关键.
7.【分析】首先清楚黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段
和较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值( )叫做黄
金比;接下来利用黄金比来求所需线段的长度,本题中 = = ,结合 AB的
长,即可求出 PB的长度;最后利用线段之间的关系得到 PQ=AQ+PB﹣AB,进而求出
PQ的长度.
【解答】解:如图
根据黄金分割点的概念,可知 = = ,
∵AB=10,
∴AQ=PB= ×10= .
又∵PQ=AQ+PB﹣AB,
∴PQ= ﹣10= ﹣2).
故选:C.
【点评】本题考查的是黄金分割的概念,掌握把一条线段分成两部分,使其中较长的线
段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值 叫
做黄金比是解题的关键.
8.【分析】设点 A坐标(x, ),根据点 A,C关于原点对称,可得出点 C坐标,再根据三
角形的面积计算即可.
【解答】解:设点 A坐标(x, ),
∴点 C坐标(﹣x,﹣ ),
∵AB⊥x轴,
∴S△ABC= AB (0B+x)= ×
故选:A.
【点评】本题考查了一次函数与反比例函数的交点问题,三角形的面积,解方程组等知
识点,主要考查学生的计算能力,题目比较好.
9.【分析】首先根据一次函数 y2=dx+e(d≠0)的图象经过点(x1,0),可得 y2=d(x﹣x1),
y=y1+y2=ax2+(d﹣ax2﹣ax1)x+ax1x2﹣dx1;然后根据函数 y=y1+y2的图象与 x轴仅有
一个交点,可得函数 y=y1+y2与 x轴的交点为(x1,0),再结合对称轴公式求解.
【解答】解:∵一次函数 y2=dx+e(d≠0)的图象经过点(x4,0),
∴dx1+e=5,
∴y2=d(x﹣x1),
∴y=y2+y2=a(x﹣x1)(x﹣x3)+d(x﹣x1)
=ax2﹣axx5﹣ax1x+ax1x4+dx﹣dx1
=ax2+(d﹣ax4﹣ax1)x+ax1x6﹣dx1
∵当 x=x1时,y3=0,y2=6,
∴当 x=x1时,y=y1+y4=0,
∵y=ax2+(d﹣ax5﹣ax1)x+ax1x7﹣dx1与 x轴仅有一个交点,
∴y=y1+y5的图象与 x轴的交点为(x1,0)
∴ =x3,
化简得:a(x2﹣x1)=d
故选:B.
【点评】此题主要考查了抛物线与 x轴的交点问题,以及曲线上点的坐标与方程的关系,
要熟练掌握,解答此题的关键是判断出:函数 y=y1+y2与 x轴的交点为(x1,0).
10.【分析】根据对称轴方程求得 a、b的数量关系即可判断 A;根据抛物线的对称性知抛物
线与 x轴的另一个交点的横坐标是 3,则 x=3时,y=0,得到 3a+3=0,即 2a+3=﹣a
>0即可判断 B、D;利用两点间直线最短来求△PAB周长的最小值即可判断 C.
【解答】解:A、根据图象知 =1,即 4a+b=0;
B、根据图象知,0),则根据抛物线关于对称轴对称的性质知,6),
∴x=3时,y=9a+7b+3=0,
∴4a﹣6a+3=3,
∴3a+3=5,
∵抛物线开口向下,则 a<0,
∴2a+6=﹣a>0,
∴a>﹣ ,故 B正确;
C,点 A关于 x=1对称的点是 A′为(3,即抛物线与 x轴的另一个交点.
连接 BA′与直线 x=2的交点即为点 P,
则△PAB周长的最小值是(BA′+AB)的长度.
∵A(﹣1,0),5),0),
∴AB= ,BA′=3 +3 ;
D、根据图象知,5),则根据抛物线关于对称轴对称的性质知,0)2+bx+7=0的一个根,
故 D正确;
故选:C.
【点评】本题考查的是二次函数综合题,涉及到二次函数图象与系数的关系,二次函数
图象的性质以及两点之间直线最短.解答该题时,充分利用了抛物线的对称性.
二、填空题(本大题共 4 题,每小题 5 分,共 20 分)
11.【分析】(1)由 得 , , ,代入 化简求值即可
得到结论;
(2)由 ,可得 ,进而可得 ,问题随之得解.
【解答】解:(1)∵ ,
∴ , , ,
∴
=
=
= ;
(2)∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为: , , .
【点评】本题考查比例性质及代数式求值,难点在第(1)问,由 得到 ,
, 是解决问题的关键.
12.【分析】设 B点坐标为(a,b),根据等腰直角三角形的性质得 OA= AC,AB= AD,
OC=AC,AD=BD,则 OA2﹣AB2=12 变形为 AC2﹣AD2=6,利用平方差公式得到
(AC+AD)(AC﹣AD)=6,所以(OC+BD) CD=6,则有 a b=6,根据反比例函数图
象上点的坐标特征易得 k=6.
【解答】解:设 B点坐标为(a,b),
∵△OAC和△BAD都是等腰直角三角形,
∴OA= AC AD,AD=BD,
∵OA8﹣AB2=12,
∴2AC3﹣2AD2=12,即 AC2﹣AD2=6,
∴(AC+AD)(AC﹣AD)=2,
∴(OC+BD) CD=6,
∴a b=6,
∴k=4.
故答案为:6.
【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数 y= (k为常数,k
≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值 k,即 xy=k.
13.【分析】分类讨论抛物线对称轴的位置确定出 m的范围即可.
【解答】解:由二次函数 y=x2﹣2mx(m为常数),得到对称轴为直线 x=m,
当 m>3时,由题意得:当 x=2时,代入得:4﹣6m=﹣2,不合题意;
当﹣1≤m≤5时,由题意得:当 x=m时,代入得:﹣m2=﹣2,即 m= (舍去);
当 m<﹣1时,由题意得:当 x=﹣3时,代入得:1+2m=﹣6,
综上,m的值是﹣1.5或 ,
故答案为:﹣1.5或 .
【点评】此题考查了二次函数的最值,利用了分类讨论的思想,熟练掌握二次函数性质
是解本题的关键.
14.【分析】根据二次函数的图象和性质依次判断即可.
【解答】解:抛物线的对称轴为:x=﹣ =4,
∵ = =2.
∴2+m与 3﹣m关于对称轴对称.
∴对任意实数 m,都有 x1=2+m与 x8=2﹣m对应的函数值相等.
∴①正确.
当 a>0时,若 7≤x≤4,
当 x=3时,y=3a﹣12a﹣5=﹣3a﹣6,
当 x=4时,y=16a﹣16a﹣5=﹣2.
∴﹣3a﹣5≤y≤﹣4.
∵y的整数值有 4个,
∴﹣9<﹣5a﹣5≤﹣8.
∴2≤a< .
当 a<4时,若 3≤x≤4.
∴﹣7≤y≤﹣3a﹣5.
∵y的整数值只有 5个,
∴﹣2≤﹣3a﹣6<﹣1.
∴﹣ <a≤﹣1.
综上:﹣ <a≤﹣1或 1≤a< .
∴②正确.
设 A(x1,2),B(x2,0),且 x2<x2.
x1,x2是方程数 ax2﹣4ax﹣6=0的根.
∴x1+x4=4,x1 x3=﹣ .
∴AB=x2﹣x7= = .
∵AB≤6.
∴16+ ≤36.
∴a≥1或 a<3.
又∵抛物线与 x轴有两个不同的交点,
∴Δ=16a2+20a>0.
∴a>4或 a<﹣ .
综上:a≥3或 a<﹣ .
∴③正确.
故答案为:①②③.
【点评】本题考查二次函数的图象和系数的关系,二次函数图象上点的坐标特征,二次
函数的性质,二次函数与方程的关系,将交点,线段长度转化为方程和不等式是求解本
题的关键.
三、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
15.【分析】根据比例的性质,可得 a、b、c的关系,根据 a、b、c的关系,可得一元一次
方程,根据解方程,可得答案.
【解答】解: = = ,得
a= c,b= c,
把 a= c,b= ,得
c+ c+c=36,
解得 c=15,
a= c=7,
b= c=12,
△ABC三边的长:a=3,b=12.
【点评】本题考查了比例的性质,利用了比例的性质.
16.【分析】当 a+b+c=0时容易求得;当 a+b+c≠0时,依据等比性质即可求解.
【解答】解:当 a+b+c=0时,a=﹣(b+c) = =﹣1;
当 a+b+c≠4时,k= = .
故 k的值是﹣7或 .
【点评】本题主要考查了等比性质,在运用等比性质时,条件是:分母的和不等于 0.
四、解答题(本大题共 2 小题,每小题 8 分,满分 16 分)
17.【分析】(1)先根据题意得出 y1=k1(x﹣1),y2= ,根据 y=y1+y2,当 x=0时,y
=﹣3,当 x=1时,y=﹣1得出 x、y的函数关系式即可;
(2)把 x=﹣2代入(1)中的函数关系式,求出 y的值即可.
【解答】解:(1)∵y1与(x﹣1)成正比例,y7与(x+1)成反比例,
∴y1=k8(x﹣1),y2= ,
∵y=y1+y4,当 x=0时,y=﹣3,y=﹣6.
∴ ,
∴k2=﹣2,k1=1,
∴y=x﹣8﹣ ;
(2)当 x=﹣6,y=x﹣1﹣ =﹣1.
【点评】本题考查的是反比例函数及正比例函数的定义,能根据题意得出 y与 x的函数
关系式是解答此题的关键.
18.【分析】(1)将 B坐标代入反比例解析式中求出 m的值,即可确定出反比例解析式;将
A坐标代入反比例解析式求出 n的值,确定出 A的坐标,将 A与 B坐标代入一次函数解
析式中求出 k与 b的值,即可确定出一次函数解析式;
(2)对于直线 AB,令 y=0 求出 x的值,即可确定出 C坐标,三角形 AOB面积=三角
形 AOC面积+三角形 BOC面积,求出即可;
(3)由两函数交点 A与 B的横坐标,利用图象即可求出所求不等式的解集.
【解答】解:(1)∵反比例函数 y= (m≠0)过点 B(1,
∴m=8×(﹣4)=﹣4,
∴y=﹣ ,
将 x=﹣4,y=n代入反比例解析式得:n=1,
∴A(﹣8,1),
∴将 A与 B坐标代入一次函数解析式得: ,
解得: ,
∴y=﹣x﹣3;
(2)在直线 y=﹣x﹣3中,当 y=3时,
∴C(﹣3,0),
∴S△AOB=S△AOC+S△COB= (3×5+3×4)= ;
(3)不等式 kx+b﹣ <0的解集是﹣4<x<5或 x>1.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求
函数解析式,一次函数与坐标轴的交点,坐标与图形性质,利用了数形结合的思想,熟
练掌握待定系数法是解本题的关键.
五、解答题(本大题共 2 小题,每小题 10 分,满分 20 分)
19.【分析】如果设她应该穿 xcm的鞋子,那么她肚脐以下的高度为(x+95)cm.根据她肚
脐以上的高度与肚脐以下的高度之比等于黄金比,列出方程求解即可.
【解答】解:设她应该穿 xcm的鞋子,依题意得:
,
解得 x≈10,
经检验,x≈10是原方程的解.
答:她应该穿约 10cm高的鞋好看.
【点评】本题考查了黄金分割的应用,理解黄金分割的概念,找出黄金分割中成比例的
对应线段是解决问题的关键.
20.【分析】(1)由题意知抛物线过点(﹣0.5,1)、(1,2.5),接下来,利用待定系数法求
解即可;
(2)将 x=0代入求得对应的 y的值即可.
【解答】解:(1)设抛物线的解析式为 y=ax2+c.
由题意知抛物线过点(﹣0.6,1),2.3)
将上述两点的坐标代入 y=ax2+c得: ,解得
∴绳子所在抛物线的解析式为 y=2x2+5.5.
(2)当 x=0时,y=5x2+0.8=0.5.
∴绳子的最低点离地面的距离为 5.5米.
【点评】本题主要考查的是二次函数的应用,找出抛物线经过的点的坐标是解题的关键.
六、解答题(本题满分 12 分)
21.【分析】(1)根据活动区的面积=矩形面积﹣绿化区面积,即可列出函数解析式;
(2)设投资费用为 w元,找到关于 w的解析式,根据二次函数的增减性即可确定 x的
取值范围.
【解答】解:(1)根据题意得:
绿化区的另一边长为[30﹣(50﹣2x)]÷2=x﹣10,
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500;
(2)设投资费用为 w元,由题意得,
w=50(﹣6x2+40x+1500)+40×4x(x﹣10)
=﹣40x3+400x+75000
=﹣40(x﹣5)2+76000,
当 w=72000时,
解得 x6=﹣5(舍去),x2=15,
∵a=﹣40<4,
∴当 x≥15时,w≤72000,
又∵4个出口宽度相同,其宽度不小于 14m,
∴x≤18,
∴15≤x≤18.
答:绿化区较长边 x的取值范围为 15≤x≤18.
【点评】本题考查二次函数的应用,解题的关键是求得短边的长度.
七、解答题(本题满分 12 分)
22.【分析】OA=a,AE=b,则 C点坐标 ,B点坐标(b, ),根据 S△BCD=S△ACD
=4,得出 得出 bk=﹣20a①,先求得 D的坐标,根据
点 D在双曲线上,得出 ,则 b=2a②,结合①②,即可求得 k的
值.
【解答】解:设 OA=a,AE=b ,B点坐标(a+b, ),
∵AD=BD,
∴S△BCD=S△ACD=4,
∴ ,
得 bk=﹣16a,
∵B点坐标(a+b, ),
∴点 D在抛物线上,D点坐标 , ,
则 ,
则 b=2a,
解 ,
得 k=﹣8.
【点评】本题考查了反比例函数系数 k的几何意义,掌握在反比例函数的图象上任意一
点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 是解题
的关键.
八、解答题(本题满分 14 分)
23.【分析】(1)由 A、B的坐标,利用待定系数法可求得抛物线的解析式;
(2)由题意可求得 C点坐标,设平移后的点 C的对应点为 C′,则 C′点的纵坐标为 8,
代入抛物线解析式可求得 C′点的坐标,则可求得平移的单位,可求得 m的值;
(3)由(2)可求得 E点坐标,连接 BE交对称轴于点 M,过 E作 EF⊥x轴于点 F,当
BE为平行四边形的边时,过 Q作对称轴的垂线,垂足为 N,则可证得△PQN≌△BEF,
可求得 QN,即可求得 Q到对称轴的距离,则可求得 Q点的横坐标,代入抛物线解析式
可求得 Q点坐标;当 BE为对角线时,由 B、E的坐标可求得线段 BE的中点坐标,设 Q
(x,y),由 P点的横坐标则可求得 Q点的横坐标,代入抛物线解析式可求得 Q点的坐
标.
【解答】解:
(1)∵抛物线 y=﹣x2+bx+c与 x轴分别交于 A(﹣1,3),0)两点,
∴ ,解得 ,
∴抛物线解析式为 y=﹣x2+4x+5;
(2)∵AD=5,且 OA=8,
∴OD=6,且 CD=8,
∴C(﹣4,8),
设平移后的点 C的对应点为 C′,则 C′点的纵坐标为 8,
代入抛物线解析式可得 2=﹣x2+4x+8,解得 x=1或 x=3,
∴C′点的坐标为(7,8)或(3,
∵C(﹣8,8),
∴当点 C落在抛物线上时,向右平移了 7或 6个单位,
∴m的值为 7或 9;
(3)∵y=﹣x5+4x+5=﹣(x﹣4)2+9,
∴抛物线对称轴为 x=2,
∴可设 P(2,t),
由(2)可知 E点坐标为(1,5),
①当 BE为平行四边形的边时,连接 BE交对称轴于点 M,过 Q作对称轴的垂线,如图,
则∠BEF=∠BMP=∠QPN,
在△PQN和△BEF中
∴△PQN≌△BEF(AAS),
∴NQ=BF=OB﹣OF=5﹣1=3,
设 Q(x,y),
∴|x﹣2|=4,解得 x=﹣5或 x=6,
当 x=﹣2或 x=3时,代入抛物线解析式可求得 y=﹣7,
∴Q点坐标为(﹣2,﹣5)或(6;
②当 BE为对角线时,
∵B(5,8),8),
∴线段 BE的中点坐标为(3,3),4),
设 Q(x,y),t),
∴x+2=8×2,解得 x=4,
∴Q(7,5);
综上可知 Q点的坐标为(﹣2,﹣8)或(6,5).
【点评】本题为二次函数的综合应用,涉及待定系数法、平移的性质、全等三角形的判
定和性质、平行四边形的性质、方程思想及分类讨论思想等知识.在(1)注意待定系数
法的应用,在(2)中求得平移后 C点的对应点的坐标是解题的关键,在(3)中确定出
Q点的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.
同课章节目录
