人教版数学7年级下册 5.2 平行线及其判定 课时练(含解析)
文档属性
| 名称 | 人教版数学7年级下册 5.2 平行线及其判定 课时练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 217.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 11:35:20 | ||
图片预览


文档简介
5.2 平行线及其判定
5.2.1 平行线的定义和画法
1.在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交
C.平行或相交 D.平行、相交或垂直
2.观察如图所示的长方体,与棱平行的棱有几条( )
A.4 B.3 C.2 D.1
3.在下面的方格纸中经过点画与线段互相平行的直线,再经过点画一条与线段垂直的直线.
4.作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段、.利用方格纸完成以下操作:
(1)过点作的平行线;
(2)过点作的平行线,与(1)中的平行线交于点;
(3)过点作的垂线.
5.2.2 平行线的基本事实及其推论
1.过直线外一点作的平行线,可以作( )条.
A.1 B.2 C.3 D.4
2.已知,是任一点,过点画一条直线与平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
3.下列说法错误的是( )
A.平面内过一点有且只有一条直线与已知直线垂直
B.两点之间的所有连线中,线段最短
C.经过两点有且只有一条直线
D.过一点有且只有一条直线与已知直线平行
4.若,,则____________________,理由是__________.
5.平行公理:______________________________________________________.
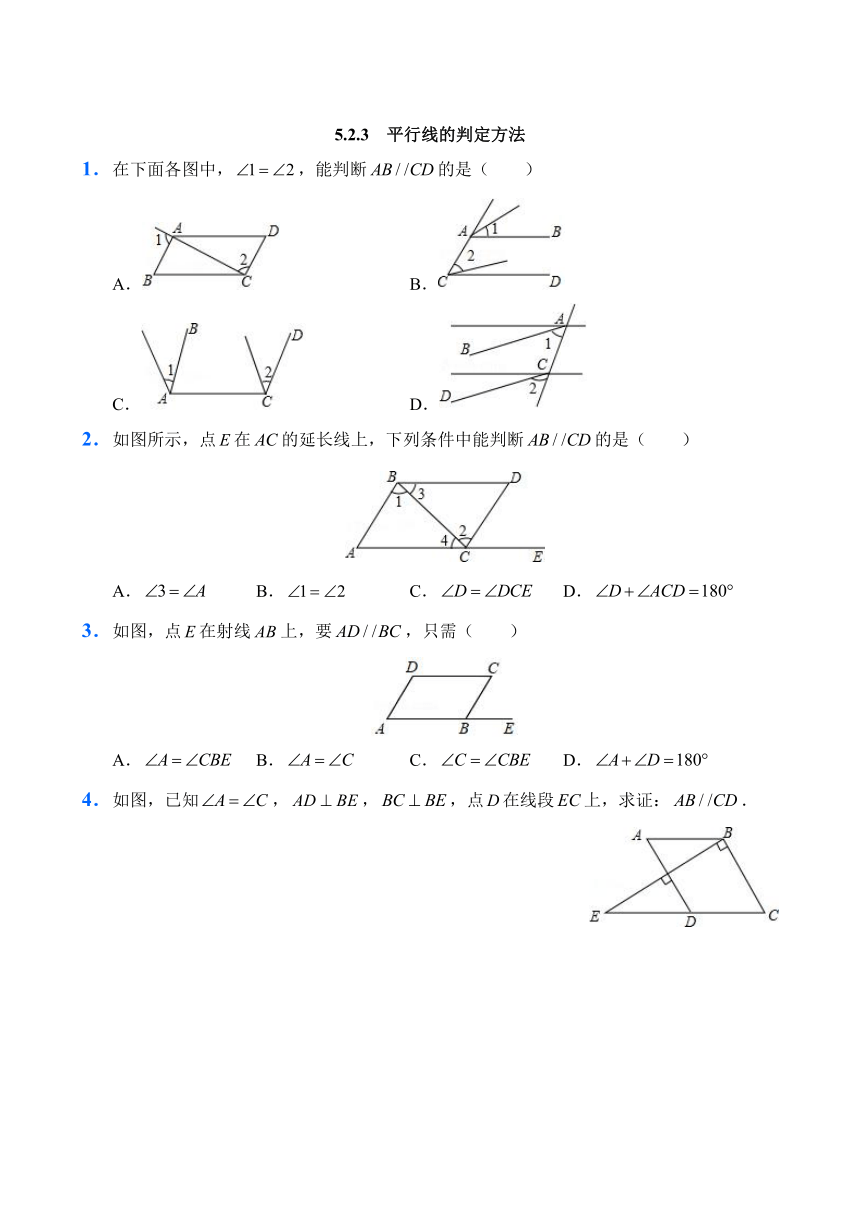
5.2.3 平行线的判定方法
1.在下面各图中,,能判断的是( )
A. B.
C. D.
2.如图所示,点在的延长线上,下列条件中能判断的是( )
A. B. C. D.
3.如图,点在射线上,要,只需( )
A. B. C. D.
4.如图,已知,,,点在线段上,求证:.
5.2 平行线及其判定
5.2.1 平行线的定义和画法
1.【答案】C
【解析】在同一平面内,不重合的两条直线只有两种位置关系:平行或相交,在同一平面内,垂直属于相交的一种特殊情况.故选C.
2.【答案】B
【解析】图中与平行的棱有:、、,共3条.故选B.
3.【答案】如图所示,
4.【答案】如图,
(1)所在的横线就是满足条件的直线,即就是所求;
(2)在直线上,到距离是5个格长的点就是,则就是所求与平行的直线;
(3)取上右边的点,过,作直线,就是所求.
5.2.2 平行线的基本事实及其推论
1.【答案】A
【解析】由平行公理“过已知直线外一点有且只有一条直线与已知直线平行”,可知只有A正确.故选A.
2.【答案】D
【解析】当点在直线上时,不能画出与平行的直线;当点不在直线上时,过点有且只有一条直线与平行,所以,这样的直线有一条或不存在.故选D.
3.【答案】D
【解析】由垂线的性质、线段的性质、直线的性质可知A、B、C正确;
由平行公理可知不正确.故选D.
4.【答案】CD EF 平行于同一条直线的两条直线互相平行
【解析】,,,
理由是:如果两条直线都和第三条直线平行,那么这两条直线平行,
故答案为:CD EF 平行于同一条直线的两条直线互相平行.
5.【答案】经过直线外一点,有且只有一条直线与这条直线平行.
【解析】由平行公理可知.
5.2.3 平行线的判定方法
1.【答案】D
【解析】图A中,、不是两条直线被第三条直线所截的内错角或同位角,不能判定;
图B中,、不是两条直线被第三条直线所截的同位角,不能判定;
图C中,、不是两条直线被第三条直线所截的同位角,不能判定;
图D中,、是两条直线被第三条直线所截的同位角,能判定;故选D.
2.【答案】B
【解析】A,,无法得到,,故A错误;
B,,根据内错角相等,两直线平行可得:,故B正确;
C,,根据内错角相等,两直线平行可得:,故C错误;
D,,根据同旁内角互补,两直线平行可得:,故D错误.故选B.
3.【答案】A
【解析】要使,只需,故选A.
4.【答案】,,,,
,,.
5.2.1 平行线的定义和画法
1.在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交
C.平行或相交 D.平行、相交或垂直
2.观察如图所示的长方体,与棱平行的棱有几条( )
A.4 B.3 C.2 D.1
3.在下面的方格纸中经过点画与线段互相平行的直线,再经过点画一条与线段垂直的直线.
4.作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段、.利用方格纸完成以下操作:
(1)过点作的平行线;
(2)过点作的平行线,与(1)中的平行线交于点;
(3)过点作的垂线.
5.2.2 平行线的基本事实及其推论
1.过直线外一点作的平行线,可以作( )条.
A.1 B.2 C.3 D.4
2.已知,是任一点,过点画一条直线与平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
3.下列说法错误的是( )
A.平面内过一点有且只有一条直线与已知直线垂直
B.两点之间的所有连线中,线段最短
C.经过两点有且只有一条直线
D.过一点有且只有一条直线与已知直线平行
4.若,,则____________________,理由是__________.
5.平行公理:______________________________________________________.
5.2.3 平行线的判定方法
1.在下面各图中,,能判断的是( )
A. B.
C. D.
2.如图所示,点在的延长线上,下列条件中能判断的是( )
A. B. C. D.
3.如图,点在射线上,要,只需( )
A. B. C. D.
4.如图,已知,,,点在线段上,求证:.
5.2 平行线及其判定
5.2.1 平行线的定义和画法
1.【答案】C
【解析】在同一平面内,不重合的两条直线只有两种位置关系:平行或相交,在同一平面内,垂直属于相交的一种特殊情况.故选C.
2.【答案】B
【解析】图中与平行的棱有:、、,共3条.故选B.
3.【答案】如图所示,
4.【答案】如图,
(1)所在的横线就是满足条件的直线,即就是所求;
(2)在直线上,到距离是5个格长的点就是,则就是所求与平行的直线;
(3)取上右边的点,过,作直线,就是所求.
5.2.2 平行线的基本事实及其推论
1.【答案】A
【解析】由平行公理“过已知直线外一点有且只有一条直线与已知直线平行”,可知只有A正确.故选A.
2.【答案】D
【解析】当点在直线上时,不能画出与平行的直线;当点不在直线上时,过点有且只有一条直线与平行,所以,这样的直线有一条或不存在.故选D.
3.【答案】D
【解析】由垂线的性质、线段的性质、直线的性质可知A、B、C正确;
由平行公理可知不正确.故选D.
4.【答案】CD EF 平行于同一条直线的两条直线互相平行
【解析】,,,
理由是:如果两条直线都和第三条直线平行,那么这两条直线平行,
故答案为:CD EF 平行于同一条直线的两条直线互相平行.
5.【答案】经过直线外一点,有且只有一条直线与这条直线平行.
【解析】由平行公理可知.
5.2.3 平行线的判定方法
1.【答案】D
【解析】图A中,、不是两条直线被第三条直线所截的内错角或同位角,不能判定;
图B中,、不是两条直线被第三条直线所截的同位角,不能判定;
图C中,、不是两条直线被第三条直线所截的同位角,不能判定;
图D中,、是两条直线被第三条直线所截的同位角,能判定;故选D.
2.【答案】B
【解析】A,,无法得到,,故A错误;
B,,根据内错角相等,两直线平行可得:,故B正确;
C,,根据内错角相等,两直线平行可得:,故C错误;
D,,根据同旁内角互补,两直线平行可得:,故D错误.故选B.
3.【答案】A
【解析】要使,只需,故选A.
4.【答案】,,,,
,,.
