数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 491.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
4.3.1 对数的概念
像上面这样的式子,已知底数和幂的值,求指数。这就是本节要学习的对数
1.情景引入
在4.2.1的问题1中,通过指数幂运算,我们能从y=
为2001年的倍数y,请思考
如果要求经过多少年游客人次是2001的2倍,3倍,4倍,….那么该如何求解
(1).=2
(2).=3
(3).=4
…
对数的概念,首先是由苏格兰数学家纳皮尔(J.Napier,1550~1617)提出的.那时候天文学是热门学科.可是由于数学的局限性,天文学家不得不花费很大精力去计算那些繁杂的“天文数字”,浪费了若干年甚至毕生的宝贵时间.纳皮尔也是一位天文爱好者,他感到,“没有什么会比数学的演算更加令人烦恼……诸如一些大数的乘、除、平方、立方、开方……因此我开始考虑……怎样才能排除这些障碍.”经过20年潜心研究大数的计算技术,他终于独立发明了对数,并于1614年出版的名著《奇妙的对数定律说明书》中阐明了对数原理,后人称为纳皮尔对数.
2.对数的发展史
3.对数的主要作用
可以简化运算
4.对数的概念
一般地,如果,(a>0,且a的对数(logarithm),记作
X=
其中a叫做对数的底数,N叫做真数
象引例中
(1).=2,所以x就是以1.11为底2的对数,记作x=;
(2).=3,所以x就是以1.11为底3的对数,记作x=;
(3).=4,;
…
底数
幂
真数
指数
以a为底N的对数
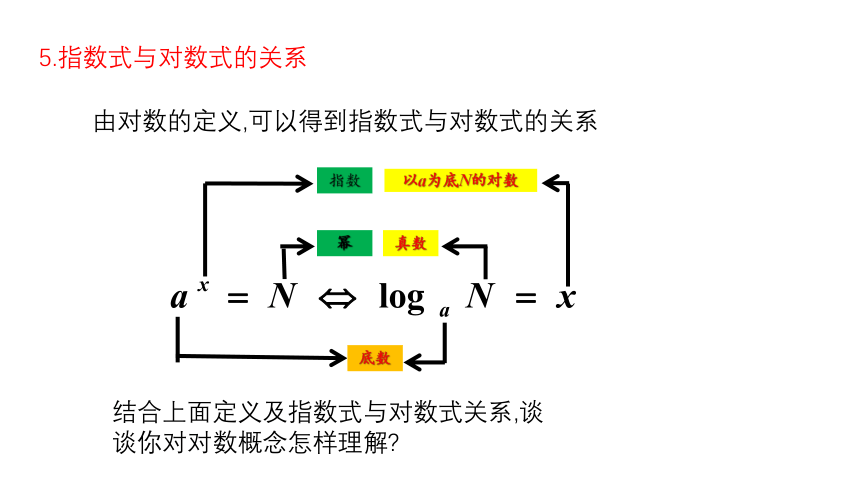
5.指数式与对数式的关系
结合上面定义及指数式与对数式关系,谈谈你对对数概念怎样理解
由对数的定义,可以得到指数式与对数式的关系
(1). 同等符号一样,表示一种运算,只不过对数运算的符号写在数的前面,即已知底数a和它的幂N求指数的运算,这种运算叫对数运算,对数运算结果仍是一个实数.
6.对数概念的理解
(2). 底数a大于0且不等于1,因为负数与0的有些指数幂没有意义,1的任何次方等于1没有研究价值
(3).真数N大于0,因为正数的任何次幂不可能为负数和0,所以负数与0没有对数
思考2:对数概念中底数N有什么限制,你能解释其中的原因吗
思考1:对数概念中为什么规定a>0,且a≠1?
7.指数式化对数式
例1.把下列指数式化为对数式(其中无理数e=2.71828…),观察对数式谈谈你的发现
(1)=10 (2) (3)
(4)=e (5)=1 (6)
(7) (8) )=1 (9) )
思考3:进行指数式与对数式互化的关键是什么?
8.两类特殊对数
在上面的(1)到(3)中化为对数式后出现了以10为底的对数,我们将以10为底的对数叫做常用对数(commonlogarithm),并把
在上面的(4)到(6)中化为对数式后出现了以无理数e=2.71828…为底数的对数,以e为底的对数称为自然对数(natural logarithm),并把
9.对数运算的两个常用结论
由 例1中的(1)(4)(7)我们发现 ,(a>0,且a
由例1中的(2)(5)(8)我们发现 , (a>0,且a
练习:把下列指数式写成对数式
(1) (2) (3)
(4) (5) (6)(
10.对数式化为指数式
例2.把下列对数式化为指数式(其中无理数e=2.71828…),并求出x的值,对比指数式中指数与对数值,谈谈你的发现
(1) (2)
(3)lg100=x (4)-ln=x
(5) (6)
11.对数恒等式
在上面的例题中如果将指数式中指数用对数值替换可以发现
,(a>0,且a
此式称为对数恒等式
思考,你能填对吗
(1)
(2)
(3)
例3.(1)求值:
(2)已知lg(x))=0,求x的值
12.应用举例
练习1:(1)求值:
(2)已知
13.课堂练习
练习2:把下列对数式写成指数式,指数式写成对数式
(1) (2)lg0.01=-2 (3)ln10=2.303
(4) (5)lgn=2.3 (6)
练习3:把下列对数式写成指数式,并求出各式中x的值
(1) (2) (3)lg0.00001=x
(4)ln (5) (6)ln
课堂小结
1.对数的概念:一般地,如果,(a>0,且a的对数 (logarithm),记作
X=
2.对数概念的理解:对数是一种运算,运算结果是一个实数
3.两类常见对数:常用对数;自然对数
4.对数运算常用的两个常用结论: ,(a>0,且a
, (a>0,且a
5.对数恒等式:
,(a>0,且a
课后作业
同步作业本
4.3.1 对数的概念
像上面这样的式子,已知底数和幂的值,求指数。这就是本节要学习的对数
1.情景引入
在4.2.1的问题1中,通过指数幂运算,我们能从y=
为2001年的倍数y,请思考
如果要求经过多少年游客人次是2001的2倍,3倍,4倍,….那么该如何求解
(1).=2
(2).=3
(3).=4
…
对数的概念,首先是由苏格兰数学家纳皮尔(J.Napier,1550~1617)提出的.那时候天文学是热门学科.可是由于数学的局限性,天文学家不得不花费很大精力去计算那些繁杂的“天文数字”,浪费了若干年甚至毕生的宝贵时间.纳皮尔也是一位天文爱好者,他感到,“没有什么会比数学的演算更加令人烦恼……诸如一些大数的乘、除、平方、立方、开方……因此我开始考虑……怎样才能排除这些障碍.”经过20年潜心研究大数的计算技术,他终于独立发明了对数,并于1614年出版的名著《奇妙的对数定律说明书》中阐明了对数原理,后人称为纳皮尔对数.
2.对数的发展史
3.对数的主要作用
可以简化运算
4.对数的概念
一般地,如果,(a>0,且a的对数(logarithm),记作
X=
其中a叫做对数的底数,N叫做真数
象引例中
(1).=2,所以x就是以1.11为底2的对数,记作x=;
(2).=3,所以x就是以1.11为底3的对数,记作x=;
(3).=4,;
…
底数
幂
真数
指数
以a为底N的对数
5.指数式与对数式的关系
结合上面定义及指数式与对数式关系,谈谈你对对数概念怎样理解
由对数的定义,可以得到指数式与对数式的关系
(1). 同等符号一样,表示一种运算,只不过对数运算的符号写在数的前面,即已知底数a和它的幂N求指数的运算,这种运算叫对数运算,对数运算结果仍是一个实数.
6.对数概念的理解
(2). 底数a大于0且不等于1,因为负数与0的有些指数幂没有意义,1的任何次方等于1没有研究价值
(3).真数N大于0,因为正数的任何次幂不可能为负数和0,所以负数与0没有对数
思考2:对数概念中底数N有什么限制,你能解释其中的原因吗
思考1:对数概念中为什么规定a>0,且a≠1?
7.指数式化对数式
例1.把下列指数式化为对数式(其中无理数e=2.71828…),观察对数式谈谈你的发现
(1)=10 (2) (3)
(4)=e (5)=1 (6)
(7) (8) )=1 (9) )
思考3:进行指数式与对数式互化的关键是什么?
8.两类特殊对数
在上面的(1)到(3)中化为对数式后出现了以10为底的对数,我们将以10为底的对数叫做常用对数(commonlogarithm),并把
在上面的(4)到(6)中化为对数式后出现了以无理数e=2.71828…为底数的对数,以e为底的对数称为自然对数(natural logarithm),并把
9.对数运算的两个常用结论
由 例1中的(1)(4)(7)我们发现 ,(a>0,且a
由例1中的(2)(5)(8)我们发现 , (a>0,且a
练习:把下列指数式写成对数式
(1) (2) (3)
(4) (5) (6)(
10.对数式化为指数式
例2.把下列对数式化为指数式(其中无理数e=2.71828…),并求出x的值,对比指数式中指数与对数值,谈谈你的发现
(1) (2)
(3)lg100=x (4)-ln=x
(5) (6)
11.对数恒等式
在上面的例题中如果将指数式中指数用对数值替换可以发现
,(a>0,且a
此式称为对数恒等式
思考,你能填对吗
(1)
(2)
(3)
例3.(1)求值:
(2)已知lg(x))=0,求x的值
12.应用举例
练习1:(1)求值:
(2)已知
13.课堂练习
练习2:把下列对数式写成指数式,指数式写成对数式
(1) (2)lg0.01=-2 (3)ln10=2.303
(4) (5)lgn=2.3 (6)
练习3:把下列对数式写成指数式,并求出各式中x的值
(1) (2) (3)lg0.00001=x
(4)ln (5) (6)ln
课堂小结
1.对数的概念:一般地,如果,(a>0,且a的对数 (logarithm),记作
X=
2.对数概念的理解:对数是一种运算,运算结果是一个实数
3.两类常见对数:常用对数;自然对数
4.对数运算常用的两个常用结论: ,(a>0,且a
, (a>0,且a
5.对数恒等式:
,(a>0,且a
课后作业
同步作业本
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
