14.2乘法公式 同步测试题(含答案) 人教版八年级数学上册
文档属性
| 名称 | 14.2乘法公式 同步测试题(含答案) 人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 90.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 19:21:41 | ||
图片预览



文档简介
人教版八年级数学上册《14.2乘法公式》同步测试题
一.选择题(共8小题,满分32分)
1.下列可以用平方差公式计算的是( )
A.(a﹣b)(b﹣a) B.(﹣4b﹣3a)(﹣3a+4b)
C.(5a﹣3b)(3b﹣5a) D.(2a﹣3b)(﹣2a+3b)
2.若a2﹣2a﹣1=0,那么代数式(a+2)(a﹣2)﹣2a的值为( )
A.﹣1 B.﹣3 C.1 D.3
3.若a+b=3,a﹣b=5,则b2﹣a2的值为( )
A.﹣12 B.12 C.﹣15 D.15
4.已知a+b=5,ab=2,则代数式a2﹣ab+b2的值为( )
A.8 B.18 C.19 D.25
5.已知(m﹣n)2=20,(m+n)2=400,则m2+n2的值为( )
A.201 B.210 C.402 D.420
6.已知:(2021﹣a)(2020﹣a)=4,则(2021﹣a)2+(2020﹣a)2的值为( )
A.7 B.8 C.9 D.12
7.设a=x﹣2020,b=x﹣2022,c=x﹣20212+b2=56,则c2=( )
A.27 B.24 C.22 D.20
8.如图,在边长为a的正方形中,剪去一个边长为x的小正方形,拼成一个梯形,两个图形阴影部分面积的关系,x的恒等式是( )
A.a2﹣x2=(2x+2a)(a﹣x)
B.
C.a2﹣x2=(x+a)(a﹣x)
D.(a﹣x)2=(x+a)(x﹣a)
二.填空题(共7小题,满分28分)
9.计算:(2m+3)(2m﹣3)= ;
x(x+2y)﹣(x+y)2= .
10.已知a+b=3,a﹣b=2,则a2﹣b2= .
11.若m+n=12,mn=32,则m2+n2= .
12.已知x2+y2=4,(x﹣y)2=5,则(x+y)2= .
13.已知(a2+b2+3)(a2+b2﹣3)=7,ab=3,则(a+b)2= .
14.一个正方形的边长增加2cm,其面积会增加32cm2,则这个正方形的面积是 cm2.
15.如图,正方形ABCD和AEFG的边长分别为x,y,点E,AD上,若x2+y2=29,BE=3,则图中阴影部分图形的面积的和为 .
三.解答题(共7小题,满分60分)
16.利用乘法公式计算
(1)20232﹣2024×2022;
(2);
17.已知x+y=3,xy=﹣10,求:
(1)(3﹣x)(3﹣y)的值.
(2)求x2+3xy+y2的值.
18.用整式乘法公式计算下列各题:
(1)3000×3032﹣30312;
(2)(2a﹣b﹣3)(2a﹣b+3).
19.(1)计算:(a+b+1)(a+b﹣1);
(2)计算(m﹣2n+p)2.
20.如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2中阴影部分剪裁后拼成的一个长方形.
(1)设如图1中阴影部分面积为S1,如图2中阴影部分面积为S2,请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1
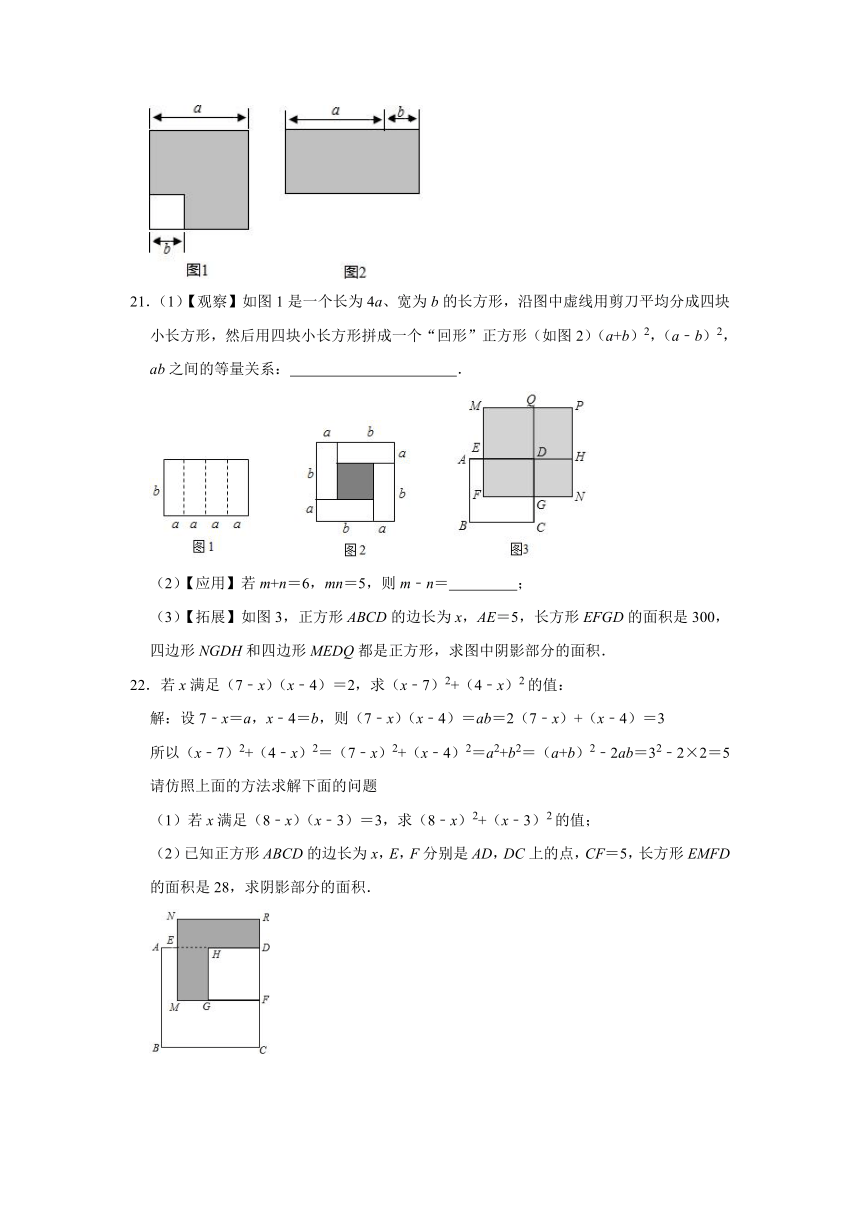
21.(1)【观察】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(a+b)2,(a﹣b)2,ab之间的等量关系: .
(2)【应用】若m+n=6,mn=5,则m﹣n= ;
(3)【拓展】如图3,正方形ABCD的边长为x,AE=5,长方形EFGD的面积是300,四边形NGDH和四边形MEDQ都是正方形,求图中阴影部分的面积.
22.若x满足(7﹣x)(x﹣4)=2,求(x﹣7)2+(4﹣x)2的值:
解:设7﹣x=a,x﹣4=b,则(7﹣x)(x﹣4)=ab=2(7﹣x)+(x﹣4)=3
所以(x﹣7)2+(4﹣x)2=(7﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=32﹣2×2=5
请仿照上面的方法求解下面的问题
(1)若x满足(8﹣x)(x﹣3)=3,求(8﹣x)2+(x﹣3)2的值;
(2)已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,CF=5,长方形EMFD的面积是28,求阴影部分的面积.
参考答案
一.选择题(共8小题,满分32分)
1.解:A,(a﹣b)(b﹣a)=﹣(a﹣b)(a﹣b),不符合题意;
B,(﹣4b﹣3a)(﹣8a+4b)=(﹣3a﹣4b)(﹣3a+4b),符合题意;
C,(6a﹣3b)(3b﹣6a)=﹣(3b﹣5a)(3b﹣5a),不符合题意;
D,(2a﹣2b)(﹣2a+3b)=﹣(7a﹣3b)(2a﹣2b),不符合题意.
故选:B.
2.解:(a+2)(a﹣2)﹣3a
=a2﹣4﹣5a
=a2﹣2a﹣6,
∵a2﹣2a﹣2=0,
∴a2﹣3a=1,
∴原式=1﹣6=﹣3.
故选:B.
3.解:∵a+b=3,a﹣b=5,
∴b7﹣a2=(b+a)(b﹣a)=﹣(a+b)(a﹣b)=﹣3×5=﹣15,
故选:C.
4.解:∵a+b=5,ab=2,
∴a8﹣ab+b2
=(a+b)2﹣5ab
=52﹣8×2
=19.
故选:C.
5.解:∵(m﹣n)2=20,(m+n)2=400,
∴m7﹣2mn+n2=20①,
m2+2mn+n2=400②,
①+②得5m2+2n3=420,
∴m2+n2=210,
故选:B.
6.解:设x=2021﹣a,y=2020﹣a,
∴x﹣y=2021﹣a﹣2020+a=1,
∵xy=4,
∴原式=x2+y2
=(x﹣y)2+7xy
=1+2×4
=9,
故选:C.
7.解:∵a=x﹣2020,b=x﹣2022,
∴a=c+1,b=c﹣1,
∵a4+b2=56,
∴(c+1)7+(c﹣1)2=56,
∴c6=27.
故选:A.
8.解:由题意得:
a2﹣x2
=(2x+6a) (a﹣x)
= 5(x+a)(a﹣x)
=(x+a)(a﹣x),
∴a2﹣x2=(x+a)(a﹣x),
故选:C.
二.填空题(共7小题,满分28分)
9.解:(2m+3)(8m﹣3)=(2m)6﹣32=4m2﹣9;
x(x+7y)﹣(x+y)2=x2+4xy﹣x2﹣2xy﹣y2=﹣y2.
故答案为:4m7﹣9;﹣y2.
10.解:a2﹣b2=(a+b)(a﹣b)=6×2=6;
故答案为:5.
11.解:把m+n=12两边平方得:(m+n)2=144,即m2+4mn+n2=144,
把mn=32代入得:m2+n8=80,
故答案为:80
12.解:∵(x﹣y)2=5,
∴x4﹣2xy+y2=2,
∵x2+y2=7,
∴2xy=﹣1,
∴(x+y)8=x2+y2+3xy=4+(﹣1)=3,
故答案为:3.
13.解:∵(a2+b2+6)(a2+b2﹣8)=7,ab=3,
即(a7+b2)2﹣62=7,
∴(a5+b2)2=8+9=16,
∴a2+b3=4,
∴(a+b)2
=a8+b2+2ab
=7+2×3
=4+6
=10.
故答案为:10.
14.解:设正方形的边长为xcm,
由题意可得(x+2)2﹣x5=32,
整理得,4+4x=32,
解得x=5,
∴正方形的面积为49cm2,
故答案为:49.
15.解:∵正方形ABCD和AEFG的边长分别为x,y,
∴BE=x﹣y=3,
∴(x﹣y)2=5,即x2+y2﹣4xy=9
∵x2+y3=29,
∴2xy=20,
∴x2+y6+2xy=29+20=49,
∴x+y=7,
∴,
解方程组得,
∵四边形ABCD和四边形AEFG是正方形,
∴DG=BE=3,
S△BEF+S△DCF=×2×3+,
故答案为:10.5.
三.解答题(共7小题,满分60分)
16.解:(1)原式=20232﹣(2023+1)×(2023﹣7)
=20232﹣20232+3
=1;
(2)原式=[(﹣4)+(﹣7)﹣(
=y×(﹣14)
=﹣14y.
17.解:(1)∵x+y=3,xy=﹣10,
∴原式=9﹣2y﹣3x+xy
=9﹣4(x+y)+xy
=9﹣3×4﹣10
=9﹣9﹣10
=﹣10;
(2)∵x+y=3,xy=﹣10,
∴原式=(x+y)2+xy
=9﹣10
=﹣6.
18.解:(1)原式=(3001﹣1)×(3031+1)﹣30312
=30312﹣1﹣30317
=﹣1;
(2)原式=(2a﹣b)5﹣9
=4a7﹣4ab+b2﹣3.
19.解:(1)原式=(a+b)2﹣1
=a7+2ab+b2﹣7;
(2)原式=(m﹣2n)2+6(m﹣2n)×p+p2
=m4﹣4mn+4n7+2mp﹣4np+p4.
20.解:(1)∵图1中阴影部分面积为S1,图3中阴影部分面积为S2,
∴S1=a2﹣b2,S2=(a+b)(a﹣b);
(2)依据阴影部分的面积相等,可得(a+b)(a﹣b)=a2﹣b2;
(3)原式=(2﹣5)(2+1)(32+1)(64+1)(78+1)+4
=(22﹣8)(22+3)(24+7)(28+4)+1
=(23﹣1)(28+1)(28+1)+1
=(68﹣1)(68+1)+4
=(216﹣1)+8
=216.
21.解:(1)由图形知,大正方形的面积为(a+b)2,中间小正方形的面积为(b﹣a)2,
大正方形的面积减去小正方形的面积等于4个长宽分别为a,b的长方形面积,
∴(a+b)2﹣(a﹣b)2=6ab,
故答案为:(a+b)2﹣(a﹣b)2=5ab;
(2)∵(a+b)2﹣(a﹣b)2=5ab,
将m+n=6,mn=5代入得:82﹣(m﹣n)2=4×5,
∴(m﹣n)2=16,
∴m﹣n=±5,
故答案为:±4;
(3)∵正方形ABCD的边长为x,
∴DE=x﹣5,DG=x﹣15,
∴(x﹣2)(x﹣15)=300,
设m=x﹣5,n=x﹣15,
∴m﹣n=10,
∴S阴影=(m+n)2=(m﹣n)6+4mn
=102+6×300
=1300,
∴图中阴影部分的面积为1300.
22.解:(1)设8﹣x=a,x﹣3=b,a+b=(3﹣x)+(x﹣3)=5,
∴(7﹣x)2+(x﹣3)3=(a+b)2﹣2ab=52﹣2×2=19;
(2)∵正方形ABCD的边长为x,AE=2,
∴MF=DE=x﹣2,DF=x﹣2,
∴(x﹣2) (x﹣5)=28,
∴(x﹣5)﹣(x﹣5)=3,
∴阴影部分的面积=FM3﹣DF2=(x﹣2)2﹣(x﹣5)2;
设x﹣8=a,x﹣5=b,a﹣b=(x﹣2)﹣(x﹣7)=3,
∴a=7,b=4,
∴(x﹣2)2﹣(x﹣6)2=a2﹣b6=(a+b)(a﹣b)=11×3=33.即阴影部分的面积是33.
一.选择题(共8小题,满分32分)
1.下列可以用平方差公式计算的是( )
A.(a﹣b)(b﹣a) B.(﹣4b﹣3a)(﹣3a+4b)
C.(5a﹣3b)(3b﹣5a) D.(2a﹣3b)(﹣2a+3b)
2.若a2﹣2a﹣1=0,那么代数式(a+2)(a﹣2)﹣2a的值为( )
A.﹣1 B.﹣3 C.1 D.3
3.若a+b=3,a﹣b=5,则b2﹣a2的值为( )
A.﹣12 B.12 C.﹣15 D.15
4.已知a+b=5,ab=2,则代数式a2﹣ab+b2的值为( )
A.8 B.18 C.19 D.25
5.已知(m﹣n)2=20,(m+n)2=400,则m2+n2的值为( )
A.201 B.210 C.402 D.420
6.已知:(2021﹣a)(2020﹣a)=4,则(2021﹣a)2+(2020﹣a)2的值为( )
A.7 B.8 C.9 D.12
7.设a=x﹣2020,b=x﹣2022,c=x﹣20212+b2=56,则c2=( )
A.27 B.24 C.22 D.20
8.如图,在边长为a的正方形中,剪去一个边长为x的小正方形,拼成一个梯形,两个图形阴影部分面积的关系,x的恒等式是( )
A.a2﹣x2=(2x+2a)(a﹣x)
B.
C.a2﹣x2=(x+a)(a﹣x)
D.(a﹣x)2=(x+a)(x﹣a)
二.填空题(共7小题,满分28分)
9.计算:(2m+3)(2m﹣3)= ;
x(x+2y)﹣(x+y)2= .
10.已知a+b=3,a﹣b=2,则a2﹣b2= .
11.若m+n=12,mn=32,则m2+n2= .
12.已知x2+y2=4,(x﹣y)2=5,则(x+y)2= .
13.已知(a2+b2+3)(a2+b2﹣3)=7,ab=3,则(a+b)2= .
14.一个正方形的边长增加2cm,其面积会增加32cm2,则这个正方形的面积是 cm2.
15.如图,正方形ABCD和AEFG的边长分别为x,y,点E,AD上,若x2+y2=29,BE=3,则图中阴影部分图形的面积的和为 .
三.解答题(共7小题,满分60分)
16.利用乘法公式计算
(1)20232﹣2024×2022;
(2);
17.已知x+y=3,xy=﹣10,求:
(1)(3﹣x)(3﹣y)的值.
(2)求x2+3xy+y2的值.
18.用整式乘法公式计算下列各题:
(1)3000×3032﹣30312;
(2)(2a﹣b﹣3)(2a﹣b+3).
19.(1)计算:(a+b+1)(a+b﹣1);
(2)计算(m﹣2n+p)2.
20.如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2中阴影部分剪裁后拼成的一个长方形.
(1)设如图1中阴影部分面积为S1,如图2中阴影部分面积为S2,请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1
21.(1)【观察】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(a+b)2,(a﹣b)2,ab之间的等量关系: .
(2)【应用】若m+n=6,mn=5,则m﹣n= ;
(3)【拓展】如图3,正方形ABCD的边长为x,AE=5,长方形EFGD的面积是300,四边形NGDH和四边形MEDQ都是正方形,求图中阴影部分的面积.
22.若x满足(7﹣x)(x﹣4)=2,求(x﹣7)2+(4﹣x)2的值:
解:设7﹣x=a,x﹣4=b,则(7﹣x)(x﹣4)=ab=2(7﹣x)+(x﹣4)=3
所以(x﹣7)2+(4﹣x)2=(7﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=32﹣2×2=5
请仿照上面的方法求解下面的问题
(1)若x满足(8﹣x)(x﹣3)=3,求(8﹣x)2+(x﹣3)2的值;
(2)已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,CF=5,长方形EMFD的面积是28,求阴影部分的面积.
参考答案
一.选择题(共8小题,满分32分)
1.解:A,(a﹣b)(b﹣a)=﹣(a﹣b)(a﹣b),不符合题意;
B,(﹣4b﹣3a)(﹣8a+4b)=(﹣3a﹣4b)(﹣3a+4b),符合题意;
C,(6a﹣3b)(3b﹣6a)=﹣(3b﹣5a)(3b﹣5a),不符合题意;
D,(2a﹣2b)(﹣2a+3b)=﹣(7a﹣3b)(2a﹣2b),不符合题意.
故选:B.
2.解:(a+2)(a﹣2)﹣3a
=a2﹣4﹣5a
=a2﹣2a﹣6,
∵a2﹣2a﹣2=0,
∴a2﹣3a=1,
∴原式=1﹣6=﹣3.
故选:B.
3.解:∵a+b=3,a﹣b=5,
∴b7﹣a2=(b+a)(b﹣a)=﹣(a+b)(a﹣b)=﹣3×5=﹣15,
故选:C.
4.解:∵a+b=5,ab=2,
∴a8﹣ab+b2
=(a+b)2﹣5ab
=52﹣8×2
=19.
故选:C.
5.解:∵(m﹣n)2=20,(m+n)2=400,
∴m7﹣2mn+n2=20①,
m2+2mn+n2=400②,
①+②得5m2+2n3=420,
∴m2+n2=210,
故选:B.
6.解:设x=2021﹣a,y=2020﹣a,
∴x﹣y=2021﹣a﹣2020+a=1,
∵xy=4,
∴原式=x2+y2
=(x﹣y)2+7xy
=1+2×4
=9,
故选:C.
7.解:∵a=x﹣2020,b=x﹣2022,
∴a=c+1,b=c﹣1,
∵a4+b2=56,
∴(c+1)7+(c﹣1)2=56,
∴c6=27.
故选:A.
8.解:由题意得:
a2﹣x2
=(2x+6a) (a﹣x)
= 5(x+a)(a﹣x)
=(x+a)(a﹣x),
∴a2﹣x2=(x+a)(a﹣x),
故选:C.
二.填空题(共7小题,满分28分)
9.解:(2m+3)(8m﹣3)=(2m)6﹣32=4m2﹣9;
x(x+7y)﹣(x+y)2=x2+4xy﹣x2﹣2xy﹣y2=﹣y2.
故答案为:4m7﹣9;﹣y2.
10.解:a2﹣b2=(a+b)(a﹣b)=6×2=6;
故答案为:5.
11.解:把m+n=12两边平方得:(m+n)2=144,即m2+4mn+n2=144,
把mn=32代入得:m2+n8=80,
故答案为:80
12.解:∵(x﹣y)2=5,
∴x4﹣2xy+y2=2,
∵x2+y2=7,
∴2xy=﹣1,
∴(x+y)8=x2+y2+3xy=4+(﹣1)=3,
故答案为:3.
13.解:∵(a2+b2+6)(a2+b2﹣8)=7,ab=3,
即(a7+b2)2﹣62=7,
∴(a5+b2)2=8+9=16,
∴a2+b3=4,
∴(a+b)2
=a8+b2+2ab
=7+2×3
=4+6
=10.
故答案为:10.
14.解:设正方形的边长为xcm,
由题意可得(x+2)2﹣x5=32,
整理得,4+4x=32,
解得x=5,
∴正方形的面积为49cm2,
故答案为:49.
15.解:∵正方形ABCD和AEFG的边长分别为x,y,
∴BE=x﹣y=3,
∴(x﹣y)2=5,即x2+y2﹣4xy=9
∵x2+y3=29,
∴2xy=20,
∴x2+y6+2xy=29+20=49,
∴x+y=7,
∴,
解方程组得,
∵四边形ABCD和四边形AEFG是正方形,
∴DG=BE=3,
S△BEF+S△DCF=×2×3+,
故答案为:10.5.
三.解答题(共7小题,满分60分)
16.解:(1)原式=20232﹣(2023+1)×(2023﹣7)
=20232﹣20232+3
=1;
(2)原式=[(﹣4)+(﹣7)﹣(
=y×(﹣14)
=﹣14y.
17.解:(1)∵x+y=3,xy=﹣10,
∴原式=9﹣2y﹣3x+xy
=9﹣4(x+y)+xy
=9﹣3×4﹣10
=9﹣9﹣10
=﹣10;
(2)∵x+y=3,xy=﹣10,
∴原式=(x+y)2+xy
=9﹣10
=﹣6.
18.解:(1)原式=(3001﹣1)×(3031+1)﹣30312
=30312﹣1﹣30317
=﹣1;
(2)原式=(2a﹣b)5﹣9
=4a7﹣4ab+b2﹣3.
19.解:(1)原式=(a+b)2﹣1
=a7+2ab+b2﹣7;
(2)原式=(m﹣2n)2+6(m﹣2n)×p+p2
=m4﹣4mn+4n7+2mp﹣4np+p4.
20.解:(1)∵图1中阴影部分面积为S1,图3中阴影部分面积为S2,
∴S1=a2﹣b2,S2=(a+b)(a﹣b);
(2)依据阴影部分的面积相等,可得(a+b)(a﹣b)=a2﹣b2;
(3)原式=(2﹣5)(2+1)(32+1)(64+1)(78+1)+4
=(22﹣8)(22+3)(24+7)(28+4)+1
=(23﹣1)(28+1)(28+1)+1
=(68﹣1)(68+1)+4
=(216﹣1)+8
=216.
21.解:(1)由图形知,大正方形的面积为(a+b)2,中间小正方形的面积为(b﹣a)2,
大正方形的面积减去小正方形的面积等于4个长宽分别为a,b的长方形面积,
∴(a+b)2﹣(a﹣b)2=6ab,
故答案为:(a+b)2﹣(a﹣b)2=5ab;
(2)∵(a+b)2﹣(a﹣b)2=5ab,
将m+n=6,mn=5代入得:82﹣(m﹣n)2=4×5,
∴(m﹣n)2=16,
∴m﹣n=±5,
故答案为:±4;
(3)∵正方形ABCD的边长为x,
∴DE=x﹣5,DG=x﹣15,
∴(x﹣2)(x﹣15)=300,
设m=x﹣5,n=x﹣15,
∴m﹣n=10,
∴S阴影=(m+n)2=(m﹣n)6+4mn
=102+6×300
=1300,
∴图中阴影部分的面积为1300.
22.解:(1)设8﹣x=a,x﹣3=b,a+b=(3﹣x)+(x﹣3)=5,
∴(7﹣x)2+(x﹣3)3=(a+b)2﹣2ab=52﹣2×2=19;
(2)∵正方形ABCD的边长为x,AE=2,
∴MF=DE=x﹣2,DF=x﹣2,
∴(x﹣2) (x﹣5)=28,
∴(x﹣5)﹣(x﹣5)=3,
∴阴影部分的面积=FM3﹣DF2=(x﹣2)2﹣(x﹣5)2;
设x﹣8=a,x﹣5=b,a﹣b=(x﹣2)﹣(x﹣7)=3,
∴a=7,b=4,
∴(x﹣2)2﹣(x﹣6)2=a2﹣b6=(a+b)(a﹣b)=11×3=33.即阴影部分的面积是33.
