反证法
图片预览




文档简介
课件11张PPT。反证法警察局里有5名嫌疑犯,他们分别做了如下口供:
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎. 聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
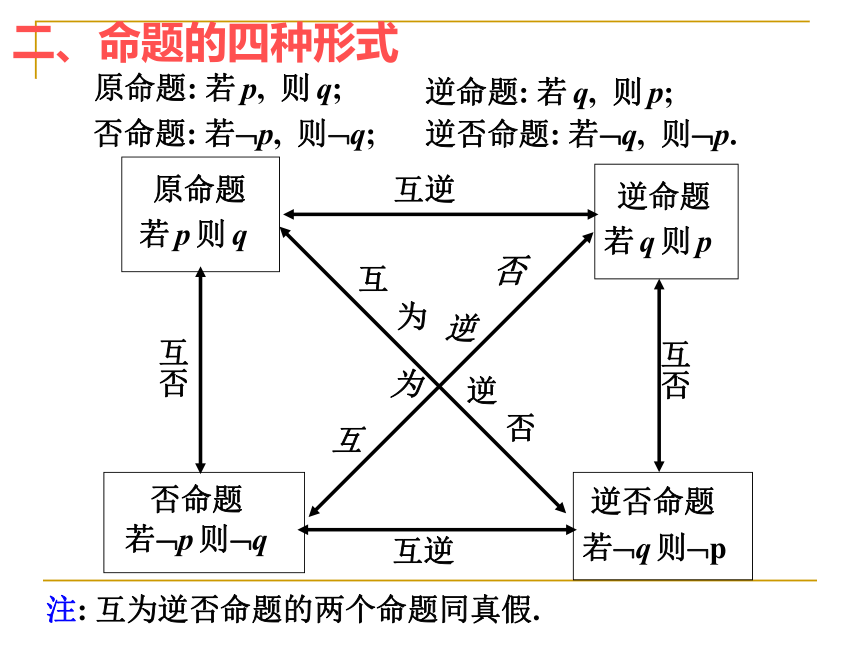
请与大家分享你的判断!快乐驿站我来当警察二、命题的四种形式逆否命题: 若?q, 则?p.原命题: 若 p, 则 q; 逆命题: 若 q, 则 p; 否命题: 若?p, 则?q; 注: 互为逆否命题的两个命题同真假. 三、反证法1.一般步骤①反设: 假设命题的结论不成立, 即假设结论的反面成立; ②归谬: 从假设出发, 经过推理论证, 得出矛盾; ③结论: 由矛盾判定假设不正确, 从而肯定命题的结论正确. 2.命题特点①结论本身以否定形式出现;②结论是“至少”、“至多”、“唯一”、“都是”等形式; ③结论涉及“存在或不存在”,“有限或无限”等形式; ④结论的反面比原结论更具体或更易于证明.证: 假设这两个方程都没有实根, 则 △1<0 且 △2<0, 从而有: △1+△2<0. 又∵△1+△2=(p12-4q1)+(p22-4q2)=p12+p22-4(q1+q2) =p12+p22-2p1p2=(p1-p2)2≥0, 与 △1+△2<0 矛盾. 即 △1+△2≥0, ∴假设不成立. 故这两个方程至少有一个有实根. 1.若 p1p2=2(q1+q2), 证明关于 x 的方程 x2+p1x+q1=0 与 x2+p2x+ q2=0 中, 至少有一个方程有实根.用反证法证明与②式相加得 -4
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎. 聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
请与大家分享你的判断!快乐驿站我来当警察二、命题的四种形式逆否命题: 若?q, 则?p.原命题: 若 p, 则 q; 逆命题: 若 q, 则 p; 否命题: 若?p, 则?q; 注: 互为逆否命题的两个命题同真假. 三、反证法1.一般步骤①反设: 假设命题的结论不成立, 即假设结论的反面成立; ②归谬: 从假设出发, 经过推理论证, 得出矛盾; ③结论: 由矛盾判定假设不正确, 从而肯定命题的结论正确. 2.命题特点①结论本身以否定形式出现;②结论是“至少”、“至多”、“唯一”、“都是”等形式; ③结论涉及“存在或不存在”,“有限或无限”等形式; ④结论的反面比原结论更具体或更易于证明.证: 假设这两个方程都没有实根, 则 △1<0 且 △2<0, 从而有: △1+△2<0. 又∵△1+△2=(p12-4q1)+(p22-4q2)=p12+p22-4(q1+q2) =p12+p22-2p1p2=(p1-p2)2≥0, 与 △1+△2<0 矛盾. 即 △1+△2≥0, ∴假设不成立. 故这两个方程至少有一个有实根. 1.若 p1p2=2(q1+q2), 证明关于 x 的方程 x2+p1x+q1=0 与 x2+p2x+ q2=0 中, 至少有一个方程有实根.用反证法证明与②式相加得 -4
