人教版六年级下册数学思维拓展第1讲浓度问题(一)(课件)(共31张PPT)
文档属性
| 名称 | 人教版六年级下册数学思维拓展第1讲浓度问题(一)(课件)(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
浓度问题的认识
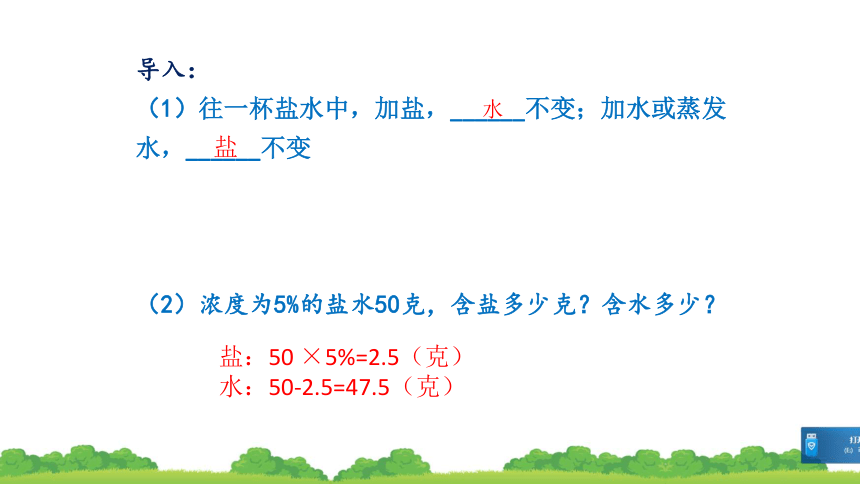
导入:
(1)往一杯盐水中,加盐,______不变;加水或蒸发水,______不变
(2)浓度为5%的盐水50克,含盐多少克?含水多少?
水
盐
盐:50 ×5%=2.5(克)
水:50-2.5=47.5(克)
导入:
(3)一杯含盐20克的盐水60克,加水得浓度为20%的盐水多少克?
(4)100克为25%的盐水,加盐得到40%的盐水多少克?
20÷20%=100(克)
100×(1-25%)÷(1-40%)=125(克)
小马过河后,驮的盐变轻了
盐
水
盐水
+
=
溶质:
通常为盐水中的“盐”,糖水中的“糖”,酒精溶液中的“酒精”等。
溶剂:
一般为水。
溶液:
溶质和溶剂的混合液体。
浓度:溶质质量与溶液质量的比值。(如:盐占盐水的百分数叫盐水的浓度)
三、比、分数、百分数、浓度的关系互化
(1)盐:水=( )
盐是水的( )
水是盐的( )
盐是盐水的( ),浓度是( ),
含水率是( )。
浓度为35%的盐水
7:13
35%
65%
(2)盐:水=1:5
盐是水的( ); 水是盐的( );
盐是盐水的( ),浓度是( )%.
含水率是( )。
5
16.67
83.33%
四、解浓度问题的诀窍
1、寻找溶液配比前后的不变量,依靠不变量求其他量。
①谁变,谁不变。
口诀:盐水一般变,加盐水不变,加水盐不变,蒸发盐不变。
②重难点:一变一不变,先算不变
变化的量÷变化的分数=不变量
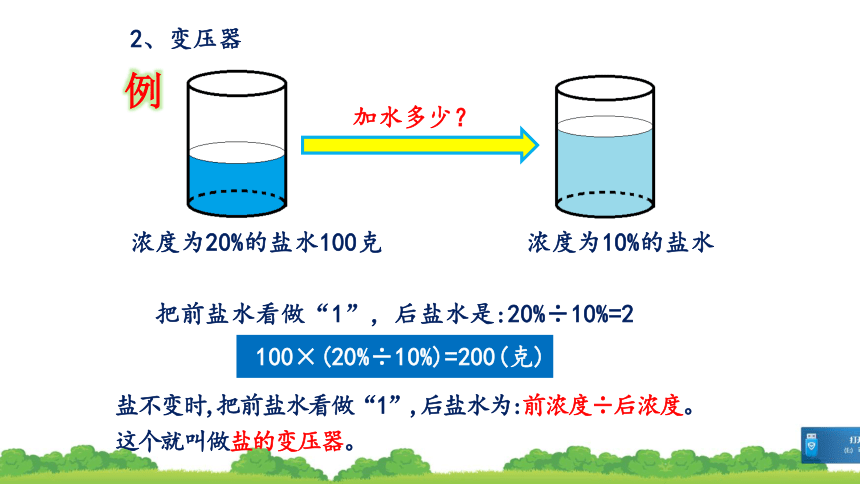
2、变压器
浓度为20%的盐水100克
加水多少?
浓度为10%的盐水
把前盐水看做“1”,后盐水是:20%÷10%=2
100×(20%÷10%)=200(克)
盐不变时,把前盐水看做“1”,后盐水为:前浓度÷后浓度。
这个就叫做盐的变压器。
例
把前盐水看做“1”,后盐水是:(1-20%)÷(1-60%)=2
100×[(1-20%)÷(1-60%)]=200(克)
水不变,把前盐水看做“1”,后盐水为:前含水率÷后含水率。
这个就叫做水的变压器。
加盐多少?
20%的盐水100克
60%的盐水
例
五、浓度问题分类
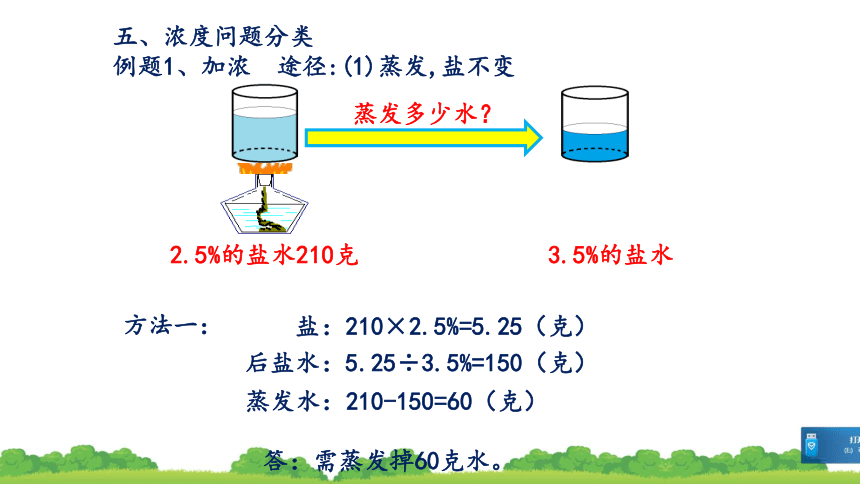
例题1、加浓 途径:(1)蒸发,盐不变
盐:210×2.5%=5.25(克)
后盐水:5.25÷3.5%=150(克)
蒸发水:210-150=60(克)
方法一:
答:需蒸发掉60克水。
2.5%的盐水210克
蒸发多少水?
3.5%的盐水
2.5%的盐水210克
蒸发多少水?
3.5%的盐水
方法二:盐的变压器
210克 “1”
蒸发水 1-2.5%÷3.5%
210×(1-2.5%÷3.5%)=60(克)
答:需要蒸发掉60克水。
盐的变压器
50kg “1”
蒸发水 1-20%÷25%
50×(1-20%÷25%)=10(kg)
答:需要蒸发掉10千克水。
20%的盐水50kg
蒸发多少水?
25%的盐水
2、仓库运来含水量为90%的一种水果100kg,一星期后含水量降低到80%,现在这批水果的质量是多少千克?
变压器:相当与盐不变
100kg “1”
现在重量 (1-90%)÷(1-80%)
100×[(1-90%)÷(1-80%)]=50(kg)
答:现在这批水果的质量是50千克
途径:(2)加盐,水不变。
方法一: 水:400×(1-40%)=240(克)
后糖水:240÷(1-50%)=480(克)
加糖:480-400=80(克)
答:需加糖80克。
加糖多少?
40%的糖水400克
50%的糖水
例2
方法二:水的变压器
加糖多少?
40%的糖水400克
50%的糖水
400克 “1”
400×[(1-40%)÷(1-50%)-1]=80(克)
答:需加糖80克。
加糖 (1-40%)÷(1-50%)-1
水的变压器
680克 “1”
680×[(1-10%)÷(1-15%)-1]=40(克)
答:需加盐40克。
加盐 (1-10%)÷(1-15%)-1
10%的盐水680克
加盐多少?
15%的盐水
2、
30%的糖水400克
50%的糖水
加糖多少?
水的变压器
400克 “1”
400×[(1-30%)÷(1-50%)-1]=160(克)
答:需加糖160克。
加糖 (1-30%)÷(1-50%)-1
25%盐水30kg
15%盐水
加水多少?
方法一: 盐: 30×25%=7.5(kg)
后盐水: 7.5÷15%=50(kg)
加水: 50-30=20(kg)
答:需加水20千克。
2、稀释
途径:加水,盐不变。
例3
方法二:盐的变压器
30kg “1”
加水 25%÷15%-1
30×(25%÷15%-1)=20(kg)
答:需加水20千克。
25%盐水30kg
15%盐水
加水多少?
加水多少?
95%的酒精600克
75%的消毒酒精
盐的变压器
600g “1”
加水 95%÷75%-1
600×(95%÷75%-1)=160(g)
答:需加水160克。
25%的盐水40kg
加水多少?
20%的盐水
盐的变压器
40kg “1”
加水 25%÷20%-1
40×(25%÷20%-1)=10(kg)
答:需加水10千克。
3、混合与配制:补偿原理的应用
配制问题:
指两种或两种以上不同浓度的溶液混合成新溶液(成品),
解题关键:所取原溶液的“盐”与成品的“盐”不变及“盐水”前后质量不变,找到两个等量关系。
解决的方法与原理:补偿原理(多盐补少盐)。
解:(10×24%+6×20%)÷(10+6)=22.5%
答:混合后的硫酸溶液的浓度是22.5%。
24%的硫酸溶液10kg
20%的硫酸溶液6kg
混合
浓度?
例4
20%的糖水300克
40%的糖水200克
混合
解:(300×20%+200×40%)÷(300+200)=28%
答:混合后的糖水浓度是28%。
浓度?
补偿原理(多盐补少盐):
例5:两种硫酸,一种浓度为60%,另一种浓度为90%,现配置浓度为70%的硫酸300克,每种硫酸各取多少?
答:浓度60%的硫酸取200克;浓度90%的硫酸取100克。
90%的硫酸取:300÷(2+1)×1=100(克)
60%的硫酸取:300÷(2+1)×2=200(克)
甲、乙两种酒精浓度分别是60%和35%,如何出配制浓度为50%的酒精500克?
60%
50%
15%
10%
35%
3
2
答:浓度60%的酒精取300克;浓度35%的酒精取200克。
60%的酒精:500÷(3+2)×3=300(克)
35%的酒精:500÷(3+2)×2=200(克)
例6:浓度为10%的盐水40kg,再加入多少千克浓度为30%的盐水,可以得到浓度为22%的盐水?
10%
22%
8%
12%
30%
2
3
40÷2×3=60(kg)
答:需要再加入60千克浓度为30%的盐水。
50%
25%
20%
25%
5%
4
5
200÷4×5=250(kg)
答:需要再加入250千克浓度为5%的硫酸溶液。
练:浓度为50%的硫酸溶液200kg,再加入多少千克浓度为5%的硫酸溶液可以配制成浓度为25%的硫酸溶液?
方法小结:
1、寻找溶液配比前后的不变量,依靠不变量求其他量。
1)谁变,谁不变。
口诀:盐水一般变,
加盐水不变,
加水盐不变,
蒸发盐不变。
2)重难点:一变一不变,先算不变(量率对应)
变化的量÷变化的分数=不变量
2、混合溶液:补偿原理。
浓度问题的认识
导入:
(1)往一杯盐水中,加盐,______不变;加水或蒸发水,______不变
(2)浓度为5%的盐水50克,含盐多少克?含水多少?
水
盐
盐:50 ×5%=2.5(克)
水:50-2.5=47.5(克)
导入:
(3)一杯含盐20克的盐水60克,加水得浓度为20%的盐水多少克?
(4)100克为25%的盐水,加盐得到40%的盐水多少克?
20÷20%=100(克)
100×(1-25%)÷(1-40%)=125(克)
小马过河后,驮的盐变轻了
盐
水
盐水
+
=
溶质:
通常为盐水中的“盐”,糖水中的“糖”,酒精溶液中的“酒精”等。
溶剂:
一般为水。
溶液:
溶质和溶剂的混合液体。
浓度:溶质质量与溶液质量的比值。(如:盐占盐水的百分数叫盐水的浓度)
三、比、分数、百分数、浓度的关系互化
(1)盐:水=( )
盐是水的( )
水是盐的( )
盐是盐水的( ),浓度是( ),
含水率是( )。
浓度为35%的盐水
7:13
35%
65%
(2)盐:水=1:5
盐是水的( ); 水是盐的( );
盐是盐水的( ),浓度是( )%.
含水率是( )。
5
16.67
83.33%
四、解浓度问题的诀窍
1、寻找溶液配比前后的不变量,依靠不变量求其他量。
①谁变,谁不变。
口诀:盐水一般变,加盐水不变,加水盐不变,蒸发盐不变。
②重难点:一变一不变,先算不变
变化的量÷变化的分数=不变量
2、变压器
浓度为20%的盐水100克
加水多少?
浓度为10%的盐水
把前盐水看做“1”,后盐水是:20%÷10%=2
100×(20%÷10%)=200(克)
盐不变时,把前盐水看做“1”,后盐水为:前浓度÷后浓度。
这个就叫做盐的变压器。
例
把前盐水看做“1”,后盐水是:(1-20%)÷(1-60%)=2
100×[(1-20%)÷(1-60%)]=200(克)
水不变,把前盐水看做“1”,后盐水为:前含水率÷后含水率。
这个就叫做水的变压器。
加盐多少?
20%的盐水100克
60%的盐水
例
五、浓度问题分类
例题1、加浓 途径:(1)蒸发,盐不变
盐:210×2.5%=5.25(克)
后盐水:5.25÷3.5%=150(克)
蒸发水:210-150=60(克)
方法一:
答:需蒸发掉60克水。
2.5%的盐水210克
蒸发多少水?
3.5%的盐水
2.5%的盐水210克
蒸发多少水?
3.5%的盐水
方法二:盐的变压器
210克 “1”
蒸发水 1-2.5%÷3.5%
210×(1-2.5%÷3.5%)=60(克)
答:需要蒸发掉60克水。
盐的变压器
50kg “1”
蒸发水 1-20%÷25%
50×(1-20%÷25%)=10(kg)
答:需要蒸发掉10千克水。
20%的盐水50kg
蒸发多少水?
25%的盐水
2、仓库运来含水量为90%的一种水果100kg,一星期后含水量降低到80%,现在这批水果的质量是多少千克?
变压器:相当与盐不变
100kg “1”
现在重量 (1-90%)÷(1-80%)
100×[(1-90%)÷(1-80%)]=50(kg)
答:现在这批水果的质量是50千克
途径:(2)加盐,水不变。
方法一: 水:400×(1-40%)=240(克)
后糖水:240÷(1-50%)=480(克)
加糖:480-400=80(克)
答:需加糖80克。
加糖多少?
40%的糖水400克
50%的糖水
例2
方法二:水的变压器
加糖多少?
40%的糖水400克
50%的糖水
400克 “1”
400×[(1-40%)÷(1-50%)-1]=80(克)
答:需加糖80克。
加糖 (1-40%)÷(1-50%)-1
水的变压器
680克 “1”
680×[(1-10%)÷(1-15%)-1]=40(克)
答:需加盐40克。
加盐 (1-10%)÷(1-15%)-1
10%的盐水680克
加盐多少?
15%的盐水
2、
30%的糖水400克
50%的糖水
加糖多少?
水的变压器
400克 “1”
400×[(1-30%)÷(1-50%)-1]=160(克)
答:需加糖160克。
加糖 (1-30%)÷(1-50%)-1
25%盐水30kg
15%盐水
加水多少?
方法一: 盐: 30×25%=7.5(kg)
后盐水: 7.5÷15%=50(kg)
加水: 50-30=20(kg)
答:需加水20千克。
2、稀释
途径:加水,盐不变。
例3
方法二:盐的变压器
30kg “1”
加水 25%÷15%-1
30×(25%÷15%-1)=20(kg)
答:需加水20千克。
25%盐水30kg
15%盐水
加水多少?
加水多少?
95%的酒精600克
75%的消毒酒精
盐的变压器
600g “1”
加水 95%÷75%-1
600×(95%÷75%-1)=160(g)
答:需加水160克。
25%的盐水40kg
加水多少?
20%的盐水
盐的变压器
40kg “1”
加水 25%÷20%-1
40×(25%÷20%-1)=10(kg)
答:需加水10千克。
3、混合与配制:补偿原理的应用
配制问题:
指两种或两种以上不同浓度的溶液混合成新溶液(成品),
解题关键:所取原溶液的“盐”与成品的“盐”不变及“盐水”前后质量不变,找到两个等量关系。
解决的方法与原理:补偿原理(多盐补少盐)。
解:(10×24%+6×20%)÷(10+6)=22.5%
答:混合后的硫酸溶液的浓度是22.5%。
24%的硫酸溶液10kg
20%的硫酸溶液6kg
混合
浓度?
例4
20%的糖水300克
40%的糖水200克
混合
解:(300×20%+200×40%)÷(300+200)=28%
答:混合后的糖水浓度是28%。
浓度?
补偿原理(多盐补少盐):
例5:两种硫酸,一种浓度为60%,另一种浓度为90%,现配置浓度为70%的硫酸300克,每种硫酸各取多少?
答:浓度60%的硫酸取200克;浓度90%的硫酸取100克。
90%的硫酸取:300÷(2+1)×1=100(克)
60%的硫酸取:300÷(2+1)×2=200(克)
甲、乙两种酒精浓度分别是60%和35%,如何出配制浓度为50%的酒精500克?
60%
50%
15%
10%
35%
3
2
答:浓度60%的酒精取300克;浓度35%的酒精取200克。
60%的酒精:500÷(3+2)×3=300(克)
35%的酒精:500÷(3+2)×2=200(克)
例6:浓度为10%的盐水40kg,再加入多少千克浓度为30%的盐水,可以得到浓度为22%的盐水?
10%
22%
8%
12%
30%
2
3
40÷2×3=60(kg)
答:需要再加入60千克浓度为30%的盐水。
50%
25%
20%
25%
5%
4
5
200÷4×5=250(kg)
答:需要再加入250千克浓度为5%的硫酸溶液。
练:浓度为50%的硫酸溶液200kg,再加入多少千克浓度为5%的硫酸溶液可以配制成浓度为25%的硫酸溶液?
方法小结:
1、寻找溶液配比前后的不变量,依靠不变量求其他量。
1)谁变,谁不变。
口诀:盐水一般变,
加盐水不变,
加水盐不变,
蒸发盐不变。
2)重难点:一变一不变,先算不变(量率对应)
变化的量÷变化的分数=不变量
2、混合溶液:补偿原理。
