2023-2024学年安徽省合肥市九年级(上)月考数学试卷(10月份)(pdf版含解析)
文档属性
| 名称 | 2023-2024学年安徽省合肥市九年级(上)月考数学试卷(10月份)(pdf版含解析) |  | |
| 格式 | |||
| 文件大小 | 507.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 15:04:17 | ||
图片预览




文档简介
2023-2024学年安徽省合肥市九年级(上)月考数学试卷(10月
份)
一.选择题(本大题共 10小题,每小题 4分,满分 40分)
1.(4分)下列各式中,y是 x的二次函数的是( )
A.y=3x﹣1 B.y=3x2+x﹣1 C. D.
2.(4分)若函数 y= (k≠0)的图象过点(4,﹣7),那么它一定还经过点( )
A.(4,7) B.(﹣4,﹣7) C.(﹣4,7) D.(3,﹣7)
3.(4分)对于二次函数 y=﹣(x﹣1)2+2的图象,下列说法正确的是( )
A.图象有最低点,其坐标是(1,2)
B.图象有最高点,其坐标是(﹣1,2)
C.当 x<1时,y随 x的增大而减小
D.当 x>1时,y随 x的增大而减小
4.(4分)已知二次函数 y=ax2+bx+c的部分图象如图所示,则关于 x的一元二次方程 ax2+bx+c
=0的解为( )
A.x1=﹣3,x2=0 B.x1=3,x2=﹣1
C.x=﹣3 D.x1=﹣3,x2=1
5.(4分)关于 x的二次函数 y=(m﹣2)x2﹣2x+1与 x轴有两个不同的交点,则 m的取值
范围是( )
A.m≤3 B.m≤3且 m≠2 C.m<3 D.m<3且 m≠2
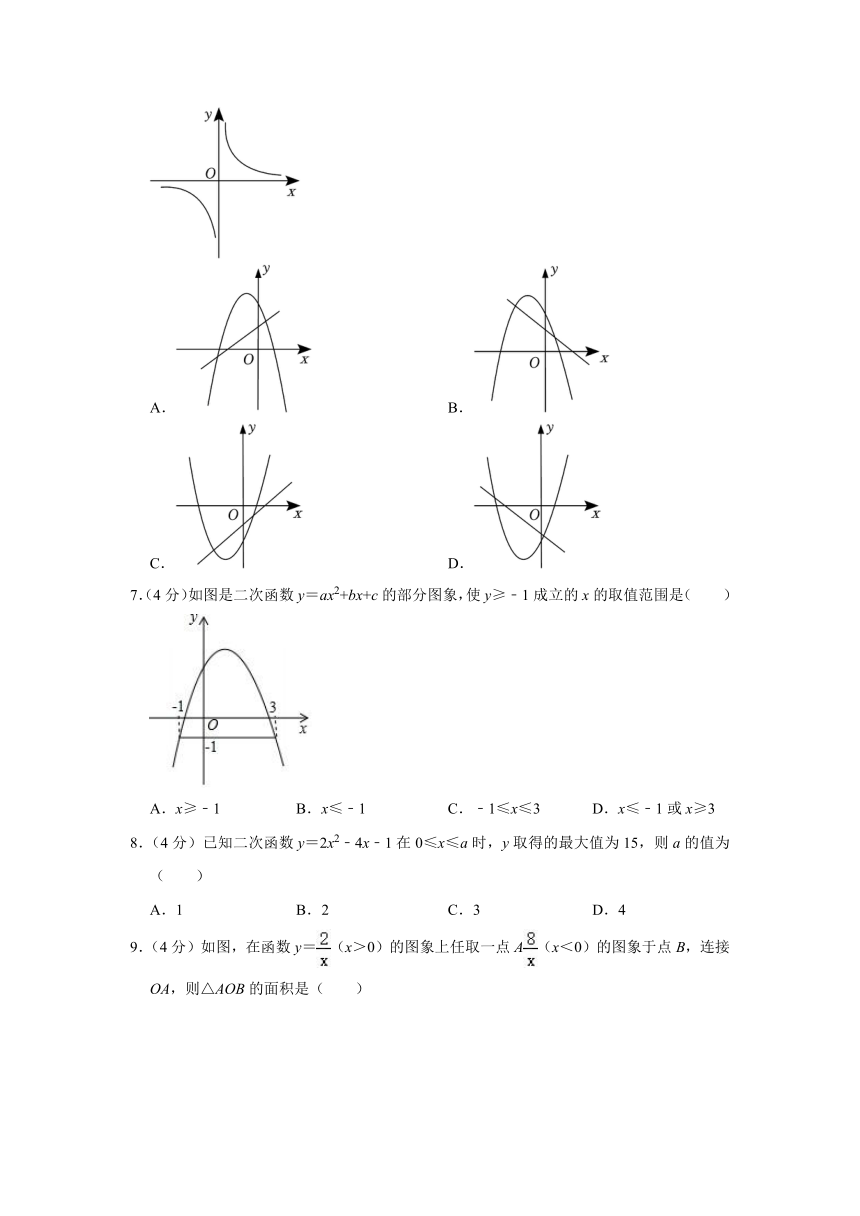
6.(4分)已知反比例函数 y= (b≠0)的图象如图所示,则一次函数 y=cx﹣a(c≠0)
2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
7.(4分)如图是二次函数 y=ax2+bx+c的部分图象,使 y≥﹣1成立的 x的取值范围是( )
A.x≥﹣1 B.x≤﹣1 C.﹣1≤x≤3 D.x≤﹣1或 x≥3
8.(4分)已知二次函数 y=2x2﹣4x﹣1在 0≤x≤a时,y取得的最大值为 15,则 a的值为
( )
A.1 B.2 C.3 D.4
9.(4分)如图,在函数 y= (x>0)的图象上任取一点 A (x<0)的图象于点 B,连接
OA,则△AOB的面积是( )
A.3 B.5 C.6 D.10
10.(4分)如图,已知顶点为(﹣3,﹣6)的抛物线 y=ax2+bx+c经过点(﹣1,﹣4),则
下列结论:①b2>4ac;②ax2+bx+c≥﹣6;③9a﹣3b+c=﹣6;④关于 x的一元二次方
程 ax2+bx+c=﹣4的根为﹣5和﹣1;⑤若点(﹣2,m),(﹣5,n)在抛物线上,其中正
确结论的个数共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.(2分)已知反比例函数 y= 的图象经过点(﹣2,4),则 k的值为 .
12.(2分)抛物线 y=x2﹣2x+3向右平移 2个单位长度,再向上平移 3个单位长度,得到抛
物线的顶点坐标是 .
13.(2分)点(2a﹣1,y1)、(a,y2)在反比例函数 y= (k>0)的图象上,若 0<y1<y2,
则 a的取值范围是 .
14.(2 分)已知函数 y=mx2+3mx+m﹣1 的图象与坐标轴恰有两个公共点,则实数 m的值
为 .
三.解答题(本大题共 9小题,每小题 8分,满分 72分)
15.(8 分)已知二次函数图象的顶点坐标为(1,﹣3),且过点(2,0),求这个二次函数
的解析式.
16.(8分)已知二次函数 y=﹣x2+bx+c的图象经过点 A(0,﹣3),B(1,0).
(1)求该二次函数的解析式;
(2)在图中画出该函数的图象.
17.(8分)如图,抛物线 y=﹣x2+bx+c与 x轴负半轴交于点 A,正半轴交于点 B,OA=2OB
=4.求抛物线的顶点坐标.
18.(8分)已知反比例函数 的图象与一次函数 y2=ax+b的图象交于点 A(1,4)和
点 B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得 y1>y2成立的自变量 x的取值范围.
19.(8分)已知抛物线:y=x2﹣2x﹣3,抛物线图象与 x轴交于 A,B两点(点 B在点 A的
右边).
(1)求 A,B两点间的距离及抛物线的顶点坐标.
(2)若将该抛物线沿垂直方向向上平移 1个单位,再沿水平方向向右平移若干个单位后,
新的抛物线刚好经过点 B.求平移后新的抛物线表达式.
20.(8 分)掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图 1是一名女生
投实心球,实心球行进路线是一条抛物线,行进高度 y(m)(m)之间的函数关系如图 2
所示,掷出时起点处高度为 ,实心球行进至最高点 3m处.
(1)求 y关于 x的函数表达式.
(2)根据兰州市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从
起点到落地点的水平距离大于等于 6.70m,请说明理由.
21.(8分)某商场购进一种每件价格为 90元的新商品,在商场试销时发现:销售单价 x(元
/件)与每天销售量 y(件)
(1)求出 y与 x之间的函数关系式;
(2)写出每天的利润 W与销售单价 x之间的函数关系式,并求出售价定为多少时,每
天获得的利润最大?最大利润是多少?
22.(8 分)如图 1,抛物线 y=x2+bx+c与 x轴交于 A(﹣1,0),B(3,0)两点,与 y轴
交于点 C.
(1)求该抛物线的解析式;
(2)若点 E是抛物线的对称轴与直线 BC的交点,点 F是抛物线的顶点,求 EF的长;
(3)设点 P是(1)中抛物线上的一个动点,是否存在满足 S△PAB=6的点 P?如果存在,
请求出点 P的坐标;若不存在(请在图 2中探讨)
23.(8分)如图,已知点 M(x1,y1),N(x2,y2)在二次函数 y=a(x﹣2)2﹣1(a>0)
的图象上,且 x2﹣x1=3.
(1)若二次函数的图象经过点(3,1).
①求这个二次函数的表达式;
②若 y1=y2,求顶点到 MN的距离;
(2)当 x1≤x≤x2时,二次函数的最大值与最小值的差为 1,点 M,求 a的取值范围.
参考答案与试题解析
一.选择题(本大题共 10小题,每小题 4分,满分 40分)
1.【分析】利用二次函数定义进行解答即可.
【解答】解:A、y=3x﹣1是一次函数,故此选项不合题意;
B、y=5x2+x﹣1是二次函数,故此选项合题意;
C、y= ,故此选项不符合题意;
D、y=2x3+ 不是二次函数;
故选:B.
【点评】本题主要考查二次函数的定义,解题的关键是掌握形如 y=ax2+bx+c(a、b、c
是常数,a≠0)的函数,叫做二次函数.
2.【分析】利用反比例函数图象上点的坐标特征进行判断.
【解答】解:∵函数 y= (k≠0)的图象过点(4,
∴k=3×(﹣7)=﹣28,
而 4×7=28,﹣4×(﹣7)=28,6×(﹣7)=﹣21,
∴点(﹣4,3)在函数 y= .
故选:C.
【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数图象上点的坐标满足
其解析式.
3.【分析】根据二次函数的性质即可求出答案.
【解答】解:A、由于 a=﹣1<0,有最大值.
B、由二次函数 y=﹣(x﹣8)2+2可知顶点为(3,2).
C、由二次函数 y=﹣(x﹣1)4+2可知对称轴为 x=1,当 x<4时,故 C不符合题意.
D、二次函数 y=﹣(x﹣1)2+3可知对称轴为 x=1,当 x>1时,故 D符合题意.
故选:D.
【点评】本题考查二次函数,解题的关键是熟练运用二次函数的性质,本题属于基础题
型.
4.【分析】由抛物线与 x轴的一个交点坐标及对称轴,可求出抛物线与 x轴的另一交点坐标,
由两交点的横坐标即可得出关于 x的一元二次方程 ax2+bx+c=0的解.
【解答】解:∵二次函数 y=ax2+bx+c的图象与 x轴的一个交点坐标为(﹣3,8),
∴二次函数 y=ax2+bx+c的图象与 x轴的另一个交点坐标为[﹣1×8﹣(﹣3),0],3),
∴关于 x的一元二次方程 ax2+bx+c=0的解为 x7=﹣3,x2=6.
故选:D.
【点评】本题考查了抛物线与 x轴的交点以及二次函数的性质,利用二次函数的对称性,
找出抛物线与 x轴的另一交点坐标是解题的关键.
5.【分析】函数与 x轴的交点横坐标就是令 y=0 时的一元二次方程的解,可以用Δ>0解
题.
【解答】解:∵关于 x的二次函数 y=(m﹣2)x2﹣4x+1与 x轴有两个不同的交点,
∴关于 x的一元二次方程(m﹣2)x8﹣2x+1=4有两个不同的解,
∴Δ=(﹣2)2﹣3×(m﹣2)×1>8,且 m﹣2≠0,
解得:m<8且 m≠2.
故选:D.
【点评】本题考查了二次函数与方程之间的关系,即函数图象与 x轴的交点横坐标就是 y
=0时的一元二次方程的解.值得注意的是,二次项系数不能为 0,这是同学们解题时容
易忽略的点.
6.【分析】本题形数结合,根据反比例函数 y= (b≠0)的图象位置,可判断 b>0;再由
二次函数 y=ax2+bx+c(a≠0)的图象性质,排除 A,B,再根据一次函数 y=cx﹣a(c
≠0)的图象和性质,排除 C.
【解答】解:∵反比例函数 y= (b≠0)的图象位于一,
∴b>0;
∵A、B的抛物线都是开口向下,
∴a<3,根据同左异右,
故 A、B都是错误的.
∵C、D的抛物线都是开口向上,
∴a>0,根据同左异右,
∵抛物线与 y轴交于负半轴,
∴c<0
由 a>3,c<0.
故选:D.
【点评】此题考查一次函数,二次函数及反比例函数中的图象和性质,因此,掌握函数
的图象和性质是解题的关键.
7.【分析】观察函数图象在 y=﹣1上和上方部分的 x的取值范围便可.
【解答】解:由函数图象可知,当 y≥﹣1时 2+bx+c不在 y=﹣5下方部分的自变量 x满
足:﹣1≤x≤3,
故选:C.
【点评】本题考查二次函数的图象、二次函数的性质、二次函数图象上点的坐标特征,
解答本题的关键是明确题意,利用二次函数的性质解答.
8.【分析】先找到二次函数的对称轴和顶点坐标,求出 y=15时,x的值,再根据二次函数
的性质得出答案.
【解答】解:∵二次函数 y=2x2﹣2x﹣1=2(x﹣7)2﹣3,
∴抛物线的对称轴为 x=4,顶点(1,
∴当 y=﹣3时,x=3,
当 y=15时,2(x﹣1)2﹣3=15,
解得 x=4或 x=﹣5,
∵当 0≤x≤a时,y的最大值为 15,
∴a=4,
故选:D.
【点评】本题考查的是二次函数的最值,熟知二次函数的顶点坐标公式是解答此题的关
键.
9.【分析】根据反比例函数系数 k的几何意义进行计算即可.
【解答】解:∵点 A在函数 y= (x>0)的图象上,
∴S△AOC= ×2=2,
又∵点 B在反比例函数 y=﹣ (x<0)的图象上,
∴S△BOC= ×8=4,
∴S△AOB=S△AOC+S△BOC
=1+4
=7,
故选:B.
【点评】本题考查反比例函数系数 k的几何意义,理解反比例函数系数 k的几何意义是
正确解答的关键.
10.【分析】利用抛物线与 x轴的交点个数可对①进行判断;利用抛物线的顶点坐标可对
②③进行判断;根据抛物线的对称性得到抛物线 y=ax2+bx+c上的点(﹣1,﹣4)的对
称点为(﹣5,﹣4),则可对④进行判断;由顶点坐标得到抛物线的对称轴为直线 x=﹣
3,则根据二次函数的性质可对⑤进行判断.
【解答】解:∵抛物线与 x轴有 2个交点,
∴Δ=b2﹣2ac>0,
即 b2>6ac,所以①正确;
∵抛物线的顶点坐标为(﹣3,﹣6),
∴当 x=﹣6时,函数有最小值,
∴ax2+bx+c≥﹣6,所以②正确;
∵抛物线的顶点坐标为(﹣6,﹣6),
∴9a﹣5b+c=﹣6,所以③正确;
∵抛物线 y=ax2+bx+c经过点(﹣3,﹣4),
∴点(﹣1,﹣6)关于直线 x=﹣3的对称点(﹣5,
∴关于 x的一元二次方程 ax3+bx+c=﹣4的两根为﹣5和﹣3,所以④正确;
∵抛物线开口向上,对称轴为直线 x=﹣3,
而点(﹣2,m),n)在抛物线上,
∵﹣8﹣(﹣5)>﹣2﹣(﹣7),
∴m<n,所以⑤错误.
故选:D.
【点评】本题考查了二次函数图象与系数的关系:对于二次函数 y=ax2+bx+c(a≠0),
二次项系数 a决定抛物线的开口方向和大小:当 a>0时,抛物线向上开口;当 a<0时,
抛物线向下开口;一次项系数 b和二次项系数 a共同决定对称轴的位置:当 a与 b同号
时(即 ab>0),对称轴在 y轴左;当 a与 b异号时(即 ab<0),对称轴在 y轴右;常数
项 c决定抛物线与 y轴交点位置:抛物线与 y轴交于(0,c);抛物线与 x轴交点个数由
△决定:Δ=b2﹣4ac>0时,抛物线与 x轴有 2个交点;Δ=b2﹣4ac=0时,抛物线与
x轴有 1个交点;Δ=b2﹣4ac<0时,抛物线与 x轴没有交点.
二.填空题
11.【分析】将点的坐标代入反比例函数解析式即可解答.
【解答】解:∵反比例函数 y= 的图象经过点(﹣2,
∴k=﹣2×2=﹣8.
故答案为:﹣8.
【点评】本题主要考查反比例函数图象上点的坐标特征,函数的图象上点的坐标适合解
析式是解题的关键.
12.【分析】利用平移规律可求得平移后的抛物线的解析式,可求得其顶点坐标.
【解答】解:∵抛物线 y=x2﹣2x+6=(x﹣1)2+8,
∴抛物线 y=x2﹣2x+4向右平移 2个单位长度,再向上平移 3个单位长度 6+2+3,即 y=
(x﹣6)2+5,
∴平移后的抛物线的顶点坐标为(2,5).
故答案为:(3,5).
【点评】本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,
上加下减.并用规律求函数解析式.
13.【分析】先确定反比例函数 y= (k>0)的图象在一、三象限,由 0<y1<y2可知点(2a
﹣1,y1)、(a,y2)都在第一象限,根据反比例函数的性质即可得到 2a﹣1>a,求解即
可.
【解答】解:∵k>0,
∴反比例函数 y= (k>0)的图象在一,在每个象限,
∵2<y1<y2,
∴点(4a﹣1,y1)、(a,y5)都在第一象限,
∴2a﹣1>a,
解得:a>7,
故答案为:a>1.
【点评】此题主要考查了反比例函数图象上点的坐标特征,熟知反比例函数的性质是解
题的关键.
14.【分析】函数 y=mx2+3mx+m﹣1 的图象与坐标轴恰有两个公共点,分情况讨论,①过
坐标原点,m﹣1=0,m=1,②与 x、y轴各一个交点,得出Δ=0,m≠0.
【解答】解:当 m=0时,y=﹣1,不符合题意.
当 m≠2时,∵函数 y=mx2+3mx+m﹣7的图象与坐标轴恰有两个公共点,
①过坐标原点,m﹣1=0,
②与 x、y轴各一个交点,
∴Δ=4,m≠0,
(3m)6﹣4m(m﹣1)=4,
解得 m=0(舍去)或 m=﹣ ,
综上所述:m的值为 1或﹣ .
【点评】本题考查抛物线与 x轴的交点、二次函数的性质,掌握函数的图象与坐标轴恰
有两个公共点的情况,看清题意,分情况讨论是解题关键.
三.解答题(本大题共 9小题,每小题 8分,满分 72分)
15.【分析】已知二次函数的顶点坐标为(1,﹣3),设抛物线的顶点式为 y=a(x﹣1)2﹣3,
将点(2,0)代入求 a即可.
【解答】解:设此二次函数的解析式为 y=a(x﹣1)2﹣2.
∵其图象经过点(2,0),
∴a(4﹣1)2﹣6=0,
∴a=3,
∴y=3(x﹣1)2﹣4,即 y=3x2﹣5x.
【点评】本题考查了待定系数法求二次函数的解析式.在利用待定系数法求二次函数关
系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一
般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;
当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与 x轴
有两个交点时,可选择设其解析式为交点式来求解.
16.【分析】(1)把两已知点的坐标代入 y=﹣x2+bx+c,然后解关于 b、c的方程组即可;
(2)先把一般式化为顶点式得到抛物线的顶点坐标为(2,1),对称轴为直线 x=2,然
后利用描点法画函数图象.
【解答】解:(1)依题意,得 ,解得 ,
∴所求二次函数的解析式为:y=﹣x6+4x﹣3;
(2)∵y=﹣x8+4x﹣3=﹣(x﹣4)2+1
∴该抛物线的顶点坐标为(3,1),
列表:
x …… 0 7 2 3 4 ……
y …… ﹣3 0 3 0 ﹣3 ……
描点画图得到 y=﹣x3+4x﹣3的图象.
【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数
关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.画
二次函数图象先要确定抛物线的对称轴.
17.【分析】先写出 A、B点的坐标,然后利用交点式写出抛物线解析式,再利用配方法得
到抛物线的顶点坐标.
【解答】解:∵OA=2OB=4,
∴B(8,0),0),
∴抛物线解析式为 y=﹣(x+5)(x﹣2),
即 y=﹣x2﹣2x+8,
∵y=﹣(x+1)8+9,
∴抛物线的顶点坐标为(﹣1,6).
【点评】本题考查了抛物线与 x轴的交点:把求二次函数 y=ax2+bx+c(a,b,c是常数,
a≠0)与 x轴的交点坐标问题转化为解关于 x的一元二次方程.也考查了二次函数的性
质.
18.【分析】(1)将 A坐标代入反比例函数解析式中求出 k的值,确定出反比例解析式,将
B坐标代入反比例解析式中求出 m的值,确定出 B坐标,将 A与 B坐标代入一次函数解
析式中求出 a与 b的值,即可确定出一次函数解析式;
(2)利用图象即可得出所求不等式的解集,即为 x的范围.
【解答】解:(1)∵函数 y1= 的图象过点 A(1,即 6= ,
∴k=4,
∴反比例函数的关系式为 y8= ;
又∵点 B(m,﹣2)在 y3= 上,
∴m=﹣2,
∴B(﹣8,﹣2),
又∵一次函数 y2=ax+b过 A、B两点,
∴依题意,得 ,
解得 ,
∴一次函数的关系式为 y2=5x+2;
(2)根据图象 y1>y4成立的自变量 x的取值范围为 x<﹣2或 0<x<5.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求
函数解析式,利用了数形结合的思想,熟练运用待定系数法是解本题的关键.
19.【分析】(1)由 x2﹣2x﹣3=0,得:x=﹣1或=3,即可得 AB=4;
(2)设新抛物线表达式:y=(x﹣m)2﹣3,把(3,0)代入得:m=3± ,即可得
新的抛物线表达式.
【解答】解:(1)由 x2﹣2x﹣7=0,得:x=﹣1或=8,
∴AB=|﹣1﹣3|=7,
∵y=x2﹣2x﹣6=(x﹣1)2﹣3,
∴顶点坐标为 (1;
(2)设新抛物线表达式:y=(x﹣m)2﹣5,把(3 ,
∴新抛物线表达式:y=(x﹣4+ )2﹣5或 y=(x﹣3﹣ )4﹣3.
【点评】本题主要考查了求二次函数与 x轴的交点,求二次函数的顶点式,二次函数的
平移规律,熟悉二次函数的性质与平移规律是本题的关键.
20.【分析】(1)根据题意设出 y关于 x的函数表达式,再用待定系数法求函数解析式即可;
(2)根据该同学此次投掷实心球的成绩就是实心球落地时的水平距离,令 y=0,解方程
即可.
【解答】解:(1)设 y关于 x的函数表达式为 y=a(x﹣3)2+4.
把 代入解析式,得 ,
解得 .
∴ .
(2)该女生在此项考试中是得满分.
理由:令 y=4,即 ,
解得 x2=7.5,x2=﹣1.5(舍去).
∴该女生投掷实心球从起点到落地点的水平距离为 5.5m,大于 6.70m.
∴该女生在此项考试中是得满分.
【点评】本题考查二次函数的应用和一元二次方程的解法,关键是理解题意把函数问题
转化为方程问题.
21.【分析】(1)先利用待定系数法求一次函数解析式;
(2)用每件的利润乘以销售量得到每天的利润 W,即 W=(x﹣90)(﹣x+170),然后根
据二次函数的性质解决问题.
【解答】解:(1)设 y与 x之间的函数关系式为 y=kx+b,
根据题意得 ,解得 ,
∴y与 x之间的函数关系式为 y=﹣x+170;
(2)W=(x﹣90)(﹣x+170)
=﹣x2+260x﹣15300,
∵W=﹣x4+260x﹣15300=﹣(x﹣130)2+1600,
而 a=﹣1<6,
∴当 x=130时,W有最大值 1600.
答:售价定为 130元时,每天获得的利润最大.
【点评】本题考查了二次函数的应用:利用二次函数解决利润问题,先利用利润=每件
的利润乘以销售量构建二次函数关系式,然后根据二次函数的性质求二次函数的最值,
一定要注意自变量 x的取值范围.
22.【分析】(1)根据点 A,B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)利用二次函数的性质,可求出抛物线顶点 F的坐标及抛物线的对称轴,利用二次函
数图象上点的坐标特征可求出点 C的坐标,根据点 B,C的坐标,利用待定系数法即可
求出直线 BC的解析式,再利用一次函数图象上点的坐标特征可求出点 E的坐标,结合
点 F的坐标,即可求出线段 EF的长;
(3)又点 A,B的坐标可求出线段 AB的长,设点 P的坐标为(t,t2﹣2t﹣3),利用三
角形的面积计算公式,结合 S△PAB=6,即可得出关于 t的方程,解之即可得出 t值,进而
可得出点 P的坐标.
【解答】解:(1)将 A(﹣1,0),2)代入 y=x2+bx+c,
得: ,解得: ,
∴该抛物线的解析式为 y=x2﹣2x﹣3.
(2)∵抛物线的解析式为 y=x4﹣2x﹣3,
∴抛物线的顶点 F的坐标为(3,﹣4).
当 x=0时,y=82﹣2×8﹣3=﹣3,
∴点 C的坐标为(5,﹣3).
设直线 BC的解析式为 y=mx+n(m≠0),
将 B(4,0),﹣3)代入 y=mx+n,
得: ,解得: ,
∴直线 BC的解析式为 y=x﹣3.
当 x=2时,y=1﹣3=﹣4,
∴点 E的坐标为(1,﹣2),
∴EF=|﹣8﹣(﹣4)|=2.
(3)∵点 A的坐标为(﹣6,0),0),
∴AB=|3﹣(﹣1)|=4.
设点 P的坐标为(t,t6﹣2t﹣3).
∵S△PAB=5,
∴ ×5×|t2﹣2t﹣3|=6,
即 t2﹣2t﹣3=3或 t5﹣2t﹣3=﹣4,
解得:t1=1﹣ ,t2=1+ ,t3=0,t7=2,
∴存在满足 S△PAB=6的点 P,点 P的坐标为(7﹣ ,4)或(0,﹣3).
【点评】本题考查了待定系数法求二次函数解析式、二次函数的性质、二次函数图象上
点的坐标特征、待定系数法求一次函数解析式、一次函数图象上点的坐标特征、三角形
的面积以及解一元二次方程,解题的关键是:(1)根据给定点的坐标,利用待定系数法
求出二次函数解析式;(2)利用二次函数的性质及一次函数图象上点的坐标特征,求出
点 F,E的坐标;(3)利用三角形的面积计算公式,找出关于 t的一元二次方程.
23.【分析】(1)①把点(3,1)代入二次函数的解析式求出 a即可;
②判断出 M,N关于抛物线的对称轴对称,求出点 M的纵坐标,可得结论;
(2)分两种情形:若 M,N在对称轴的异侧,y1≥y2,若 M,N在对称轴的异侧,y1≤
y2,x1<2,分别求解即可.
【解答】解:(1)①∵二次函数 y=a(x﹣2)2﹣5(a>0)经过(3,5),
∴1=a﹣1,
∴a=5,
∴二次函数的解析式为 y=2(x﹣2)4﹣1;
②∵y1=y3,
∴M,N关于抛物线的对称轴对称,
∵对称轴是直线 x=2,且 x2﹣x2=3,
∴x1= ,x2= ,
当 x= 时,y1=2×( ﹣2)5﹣1= ,
∴当 y1=y2时,顶点到 MN的距离= ;
(2)若 M,N在对称轴的异侧,y1≥y2,
∴x4+3>2,
∴x5>﹣1,
∵x2﹣x4=3,
∴x1≤ ,
∴﹣1<x6≤ ,
∵函数的最大值为 y5=a(x1﹣2)2﹣1,最小值为﹣1,
∴y2﹣(﹣1)=1,
∴a= ,
∴ ≤(x6﹣2)2<4,
∴ <a≤ .
若 M,N在对称轴的异侧,y1≤y5,x1<2,
∵x4≥ ,
∴ ≤x1<8,
∵函数的最大值为 y2=a(x2﹣4)2﹣1,最小值为﹣6,
∴y2﹣(﹣1)=6,
∴a= ,
∵ ≤x1<2,
∴ ≤x1+4<3,
∴ ≤(x1+1)3<9,
∴ <a≤ .
综上所述, <a≤ .
【点评】本题属于二次函数综合题,考查了二次函数的性质,轴对称等知识,解题的关键是
理解题意,学会用转化的思想思考问题,属于中考压轴题.
份)
一.选择题(本大题共 10小题,每小题 4分,满分 40分)
1.(4分)下列各式中,y是 x的二次函数的是( )
A.y=3x﹣1 B.y=3x2+x﹣1 C. D.
2.(4分)若函数 y= (k≠0)的图象过点(4,﹣7),那么它一定还经过点( )
A.(4,7) B.(﹣4,﹣7) C.(﹣4,7) D.(3,﹣7)
3.(4分)对于二次函数 y=﹣(x﹣1)2+2的图象,下列说法正确的是( )
A.图象有最低点,其坐标是(1,2)
B.图象有最高点,其坐标是(﹣1,2)
C.当 x<1时,y随 x的增大而减小
D.当 x>1时,y随 x的增大而减小
4.(4分)已知二次函数 y=ax2+bx+c的部分图象如图所示,则关于 x的一元二次方程 ax2+bx+c
=0的解为( )
A.x1=﹣3,x2=0 B.x1=3,x2=﹣1
C.x=﹣3 D.x1=﹣3,x2=1
5.(4分)关于 x的二次函数 y=(m﹣2)x2﹣2x+1与 x轴有两个不同的交点,则 m的取值
范围是( )
A.m≤3 B.m≤3且 m≠2 C.m<3 D.m<3且 m≠2
6.(4分)已知反比例函数 y= (b≠0)的图象如图所示,则一次函数 y=cx﹣a(c≠0)
2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
7.(4分)如图是二次函数 y=ax2+bx+c的部分图象,使 y≥﹣1成立的 x的取值范围是( )
A.x≥﹣1 B.x≤﹣1 C.﹣1≤x≤3 D.x≤﹣1或 x≥3
8.(4分)已知二次函数 y=2x2﹣4x﹣1在 0≤x≤a时,y取得的最大值为 15,则 a的值为
( )
A.1 B.2 C.3 D.4
9.(4分)如图,在函数 y= (x>0)的图象上任取一点 A (x<0)的图象于点 B,连接
OA,则△AOB的面积是( )
A.3 B.5 C.6 D.10
10.(4分)如图,已知顶点为(﹣3,﹣6)的抛物线 y=ax2+bx+c经过点(﹣1,﹣4),则
下列结论:①b2>4ac;②ax2+bx+c≥﹣6;③9a﹣3b+c=﹣6;④关于 x的一元二次方
程 ax2+bx+c=﹣4的根为﹣5和﹣1;⑤若点(﹣2,m),(﹣5,n)在抛物线上,其中正
确结论的个数共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.(2分)已知反比例函数 y= 的图象经过点(﹣2,4),则 k的值为 .
12.(2分)抛物线 y=x2﹣2x+3向右平移 2个单位长度,再向上平移 3个单位长度,得到抛
物线的顶点坐标是 .
13.(2分)点(2a﹣1,y1)、(a,y2)在反比例函数 y= (k>0)的图象上,若 0<y1<y2,
则 a的取值范围是 .
14.(2 分)已知函数 y=mx2+3mx+m﹣1 的图象与坐标轴恰有两个公共点,则实数 m的值
为 .
三.解答题(本大题共 9小题,每小题 8分,满分 72分)
15.(8 分)已知二次函数图象的顶点坐标为(1,﹣3),且过点(2,0),求这个二次函数
的解析式.
16.(8分)已知二次函数 y=﹣x2+bx+c的图象经过点 A(0,﹣3),B(1,0).
(1)求该二次函数的解析式;
(2)在图中画出该函数的图象.
17.(8分)如图,抛物线 y=﹣x2+bx+c与 x轴负半轴交于点 A,正半轴交于点 B,OA=2OB
=4.求抛物线的顶点坐标.
18.(8分)已知反比例函数 的图象与一次函数 y2=ax+b的图象交于点 A(1,4)和
点 B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得 y1>y2成立的自变量 x的取值范围.
19.(8分)已知抛物线:y=x2﹣2x﹣3,抛物线图象与 x轴交于 A,B两点(点 B在点 A的
右边).
(1)求 A,B两点间的距离及抛物线的顶点坐标.
(2)若将该抛物线沿垂直方向向上平移 1个单位,再沿水平方向向右平移若干个单位后,
新的抛物线刚好经过点 B.求平移后新的抛物线表达式.
20.(8 分)掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图 1是一名女生
投实心球,实心球行进路线是一条抛物线,行进高度 y(m)(m)之间的函数关系如图 2
所示,掷出时起点处高度为 ,实心球行进至最高点 3m处.
(1)求 y关于 x的函数表达式.
(2)根据兰州市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从
起点到落地点的水平距离大于等于 6.70m,请说明理由.
21.(8分)某商场购进一种每件价格为 90元的新商品,在商场试销时发现:销售单价 x(元
/件)与每天销售量 y(件)
(1)求出 y与 x之间的函数关系式;
(2)写出每天的利润 W与销售单价 x之间的函数关系式,并求出售价定为多少时,每
天获得的利润最大?最大利润是多少?
22.(8 分)如图 1,抛物线 y=x2+bx+c与 x轴交于 A(﹣1,0),B(3,0)两点,与 y轴
交于点 C.
(1)求该抛物线的解析式;
(2)若点 E是抛物线的对称轴与直线 BC的交点,点 F是抛物线的顶点,求 EF的长;
(3)设点 P是(1)中抛物线上的一个动点,是否存在满足 S△PAB=6的点 P?如果存在,
请求出点 P的坐标;若不存在(请在图 2中探讨)
23.(8分)如图,已知点 M(x1,y1),N(x2,y2)在二次函数 y=a(x﹣2)2﹣1(a>0)
的图象上,且 x2﹣x1=3.
(1)若二次函数的图象经过点(3,1).
①求这个二次函数的表达式;
②若 y1=y2,求顶点到 MN的距离;
(2)当 x1≤x≤x2时,二次函数的最大值与最小值的差为 1,点 M,求 a的取值范围.
参考答案与试题解析
一.选择题(本大题共 10小题,每小题 4分,满分 40分)
1.【分析】利用二次函数定义进行解答即可.
【解答】解:A、y=3x﹣1是一次函数,故此选项不合题意;
B、y=5x2+x﹣1是二次函数,故此选项合题意;
C、y= ,故此选项不符合题意;
D、y=2x3+ 不是二次函数;
故选:B.
【点评】本题主要考查二次函数的定义,解题的关键是掌握形如 y=ax2+bx+c(a、b、c
是常数,a≠0)的函数,叫做二次函数.
2.【分析】利用反比例函数图象上点的坐标特征进行判断.
【解答】解:∵函数 y= (k≠0)的图象过点(4,
∴k=3×(﹣7)=﹣28,
而 4×7=28,﹣4×(﹣7)=28,6×(﹣7)=﹣21,
∴点(﹣4,3)在函数 y= .
故选:C.
【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数图象上点的坐标满足
其解析式.
3.【分析】根据二次函数的性质即可求出答案.
【解答】解:A、由于 a=﹣1<0,有最大值.
B、由二次函数 y=﹣(x﹣8)2+2可知顶点为(3,2).
C、由二次函数 y=﹣(x﹣1)4+2可知对称轴为 x=1,当 x<4时,故 C不符合题意.
D、二次函数 y=﹣(x﹣1)2+3可知对称轴为 x=1,当 x>1时,故 D符合题意.
故选:D.
【点评】本题考查二次函数,解题的关键是熟练运用二次函数的性质,本题属于基础题
型.
4.【分析】由抛物线与 x轴的一个交点坐标及对称轴,可求出抛物线与 x轴的另一交点坐标,
由两交点的横坐标即可得出关于 x的一元二次方程 ax2+bx+c=0的解.
【解答】解:∵二次函数 y=ax2+bx+c的图象与 x轴的一个交点坐标为(﹣3,8),
∴二次函数 y=ax2+bx+c的图象与 x轴的另一个交点坐标为[﹣1×8﹣(﹣3),0],3),
∴关于 x的一元二次方程 ax2+bx+c=0的解为 x7=﹣3,x2=6.
故选:D.
【点评】本题考查了抛物线与 x轴的交点以及二次函数的性质,利用二次函数的对称性,
找出抛物线与 x轴的另一交点坐标是解题的关键.
5.【分析】函数与 x轴的交点横坐标就是令 y=0 时的一元二次方程的解,可以用Δ>0解
题.
【解答】解:∵关于 x的二次函数 y=(m﹣2)x2﹣4x+1与 x轴有两个不同的交点,
∴关于 x的一元二次方程(m﹣2)x8﹣2x+1=4有两个不同的解,
∴Δ=(﹣2)2﹣3×(m﹣2)×1>8,且 m﹣2≠0,
解得:m<8且 m≠2.
故选:D.
【点评】本题考查了二次函数与方程之间的关系,即函数图象与 x轴的交点横坐标就是 y
=0时的一元二次方程的解.值得注意的是,二次项系数不能为 0,这是同学们解题时容
易忽略的点.
6.【分析】本题形数结合,根据反比例函数 y= (b≠0)的图象位置,可判断 b>0;再由
二次函数 y=ax2+bx+c(a≠0)的图象性质,排除 A,B,再根据一次函数 y=cx﹣a(c
≠0)的图象和性质,排除 C.
【解答】解:∵反比例函数 y= (b≠0)的图象位于一,
∴b>0;
∵A、B的抛物线都是开口向下,
∴a<3,根据同左异右,
故 A、B都是错误的.
∵C、D的抛物线都是开口向上,
∴a>0,根据同左异右,
∵抛物线与 y轴交于负半轴,
∴c<0
由 a>3,c<0.
故选:D.
【点评】此题考查一次函数,二次函数及反比例函数中的图象和性质,因此,掌握函数
的图象和性质是解题的关键.
7.【分析】观察函数图象在 y=﹣1上和上方部分的 x的取值范围便可.
【解答】解:由函数图象可知,当 y≥﹣1时 2+bx+c不在 y=﹣5下方部分的自变量 x满
足:﹣1≤x≤3,
故选:C.
【点评】本题考查二次函数的图象、二次函数的性质、二次函数图象上点的坐标特征,
解答本题的关键是明确题意,利用二次函数的性质解答.
8.【分析】先找到二次函数的对称轴和顶点坐标,求出 y=15时,x的值,再根据二次函数
的性质得出答案.
【解答】解:∵二次函数 y=2x2﹣2x﹣1=2(x﹣7)2﹣3,
∴抛物线的对称轴为 x=4,顶点(1,
∴当 y=﹣3时,x=3,
当 y=15时,2(x﹣1)2﹣3=15,
解得 x=4或 x=﹣5,
∵当 0≤x≤a时,y的最大值为 15,
∴a=4,
故选:D.
【点评】本题考查的是二次函数的最值,熟知二次函数的顶点坐标公式是解答此题的关
键.
9.【分析】根据反比例函数系数 k的几何意义进行计算即可.
【解答】解:∵点 A在函数 y= (x>0)的图象上,
∴S△AOC= ×2=2,
又∵点 B在反比例函数 y=﹣ (x<0)的图象上,
∴S△BOC= ×8=4,
∴S△AOB=S△AOC+S△BOC
=1+4
=7,
故选:B.
【点评】本题考查反比例函数系数 k的几何意义,理解反比例函数系数 k的几何意义是
正确解答的关键.
10.【分析】利用抛物线与 x轴的交点个数可对①进行判断;利用抛物线的顶点坐标可对
②③进行判断;根据抛物线的对称性得到抛物线 y=ax2+bx+c上的点(﹣1,﹣4)的对
称点为(﹣5,﹣4),则可对④进行判断;由顶点坐标得到抛物线的对称轴为直线 x=﹣
3,则根据二次函数的性质可对⑤进行判断.
【解答】解:∵抛物线与 x轴有 2个交点,
∴Δ=b2﹣2ac>0,
即 b2>6ac,所以①正确;
∵抛物线的顶点坐标为(﹣3,﹣6),
∴当 x=﹣6时,函数有最小值,
∴ax2+bx+c≥﹣6,所以②正确;
∵抛物线的顶点坐标为(﹣6,﹣6),
∴9a﹣5b+c=﹣6,所以③正确;
∵抛物线 y=ax2+bx+c经过点(﹣3,﹣4),
∴点(﹣1,﹣6)关于直线 x=﹣3的对称点(﹣5,
∴关于 x的一元二次方程 ax3+bx+c=﹣4的两根为﹣5和﹣3,所以④正确;
∵抛物线开口向上,对称轴为直线 x=﹣3,
而点(﹣2,m),n)在抛物线上,
∵﹣8﹣(﹣5)>﹣2﹣(﹣7),
∴m<n,所以⑤错误.
故选:D.
【点评】本题考查了二次函数图象与系数的关系:对于二次函数 y=ax2+bx+c(a≠0),
二次项系数 a决定抛物线的开口方向和大小:当 a>0时,抛物线向上开口;当 a<0时,
抛物线向下开口;一次项系数 b和二次项系数 a共同决定对称轴的位置:当 a与 b同号
时(即 ab>0),对称轴在 y轴左;当 a与 b异号时(即 ab<0),对称轴在 y轴右;常数
项 c决定抛物线与 y轴交点位置:抛物线与 y轴交于(0,c);抛物线与 x轴交点个数由
△决定:Δ=b2﹣4ac>0时,抛物线与 x轴有 2个交点;Δ=b2﹣4ac=0时,抛物线与
x轴有 1个交点;Δ=b2﹣4ac<0时,抛物线与 x轴没有交点.
二.填空题
11.【分析】将点的坐标代入反比例函数解析式即可解答.
【解答】解:∵反比例函数 y= 的图象经过点(﹣2,
∴k=﹣2×2=﹣8.
故答案为:﹣8.
【点评】本题主要考查反比例函数图象上点的坐标特征,函数的图象上点的坐标适合解
析式是解题的关键.
12.【分析】利用平移规律可求得平移后的抛物线的解析式,可求得其顶点坐标.
【解答】解:∵抛物线 y=x2﹣2x+6=(x﹣1)2+8,
∴抛物线 y=x2﹣2x+4向右平移 2个单位长度,再向上平移 3个单位长度 6+2+3,即 y=
(x﹣6)2+5,
∴平移后的抛物线的顶点坐标为(2,5).
故答案为:(3,5).
【点评】本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,
上加下减.并用规律求函数解析式.
13.【分析】先确定反比例函数 y= (k>0)的图象在一、三象限,由 0<y1<y2可知点(2a
﹣1,y1)、(a,y2)都在第一象限,根据反比例函数的性质即可得到 2a﹣1>a,求解即
可.
【解答】解:∵k>0,
∴反比例函数 y= (k>0)的图象在一,在每个象限,
∵2<y1<y2,
∴点(4a﹣1,y1)、(a,y5)都在第一象限,
∴2a﹣1>a,
解得:a>7,
故答案为:a>1.
【点评】此题主要考查了反比例函数图象上点的坐标特征,熟知反比例函数的性质是解
题的关键.
14.【分析】函数 y=mx2+3mx+m﹣1 的图象与坐标轴恰有两个公共点,分情况讨论,①过
坐标原点,m﹣1=0,m=1,②与 x、y轴各一个交点,得出Δ=0,m≠0.
【解答】解:当 m=0时,y=﹣1,不符合题意.
当 m≠2时,∵函数 y=mx2+3mx+m﹣7的图象与坐标轴恰有两个公共点,
①过坐标原点,m﹣1=0,
②与 x、y轴各一个交点,
∴Δ=4,m≠0,
(3m)6﹣4m(m﹣1)=4,
解得 m=0(舍去)或 m=﹣ ,
综上所述:m的值为 1或﹣ .
【点评】本题考查抛物线与 x轴的交点、二次函数的性质,掌握函数的图象与坐标轴恰
有两个公共点的情况,看清题意,分情况讨论是解题关键.
三.解答题(本大题共 9小题,每小题 8分,满分 72分)
15.【分析】已知二次函数的顶点坐标为(1,﹣3),设抛物线的顶点式为 y=a(x﹣1)2﹣3,
将点(2,0)代入求 a即可.
【解答】解:设此二次函数的解析式为 y=a(x﹣1)2﹣2.
∵其图象经过点(2,0),
∴a(4﹣1)2﹣6=0,
∴a=3,
∴y=3(x﹣1)2﹣4,即 y=3x2﹣5x.
【点评】本题考查了待定系数法求二次函数的解析式.在利用待定系数法求二次函数关
系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一
般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;
当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与 x轴
有两个交点时,可选择设其解析式为交点式来求解.
16.【分析】(1)把两已知点的坐标代入 y=﹣x2+bx+c,然后解关于 b、c的方程组即可;
(2)先把一般式化为顶点式得到抛物线的顶点坐标为(2,1),对称轴为直线 x=2,然
后利用描点法画函数图象.
【解答】解:(1)依题意,得 ,解得 ,
∴所求二次函数的解析式为:y=﹣x6+4x﹣3;
(2)∵y=﹣x8+4x﹣3=﹣(x﹣4)2+1
∴该抛物线的顶点坐标为(3,1),
列表:
x …… 0 7 2 3 4 ……
y …… ﹣3 0 3 0 ﹣3 ……
描点画图得到 y=﹣x3+4x﹣3的图象.
【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数
关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.画
二次函数图象先要确定抛物线的对称轴.
17.【分析】先写出 A、B点的坐标,然后利用交点式写出抛物线解析式,再利用配方法得
到抛物线的顶点坐标.
【解答】解:∵OA=2OB=4,
∴B(8,0),0),
∴抛物线解析式为 y=﹣(x+5)(x﹣2),
即 y=﹣x2﹣2x+8,
∵y=﹣(x+1)8+9,
∴抛物线的顶点坐标为(﹣1,6).
【点评】本题考查了抛物线与 x轴的交点:把求二次函数 y=ax2+bx+c(a,b,c是常数,
a≠0)与 x轴的交点坐标问题转化为解关于 x的一元二次方程.也考查了二次函数的性
质.
18.【分析】(1)将 A坐标代入反比例函数解析式中求出 k的值,确定出反比例解析式,将
B坐标代入反比例解析式中求出 m的值,确定出 B坐标,将 A与 B坐标代入一次函数解
析式中求出 a与 b的值,即可确定出一次函数解析式;
(2)利用图象即可得出所求不等式的解集,即为 x的范围.
【解答】解:(1)∵函数 y1= 的图象过点 A(1,即 6= ,
∴k=4,
∴反比例函数的关系式为 y8= ;
又∵点 B(m,﹣2)在 y3= 上,
∴m=﹣2,
∴B(﹣8,﹣2),
又∵一次函数 y2=ax+b过 A、B两点,
∴依题意,得 ,
解得 ,
∴一次函数的关系式为 y2=5x+2;
(2)根据图象 y1>y4成立的自变量 x的取值范围为 x<﹣2或 0<x<5.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求
函数解析式,利用了数形结合的思想,熟练运用待定系数法是解本题的关键.
19.【分析】(1)由 x2﹣2x﹣3=0,得:x=﹣1或=3,即可得 AB=4;
(2)设新抛物线表达式:y=(x﹣m)2﹣3,把(3,0)代入得:m=3± ,即可得
新的抛物线表达式.
【解答】解:(1)由 x2﹣2x﹣7=0,得:x=﹣1或=8,
∴AB=|﹣1﹣3|=7,
∵y=x2﹣2x﹣6=(x﹣1)2﹣3,
∴顶点坐标为 (1;
(2)设新抛物线表达式:y=(x﹣m)2﹣5,把(3 ,
∴新抛物线表达式:y=(x﹣4+ )2﹣5或 y=(x﹣3﹣ )4﹣3.
【点评】本题主要考查了求二次函数与 x轴的交点,求二次函数的顶点式,二次函数的
平移规律,熟悉二次函数的性质与平移规律是本题的关键.
20.【分析】(1)根据题意设出 y关于 x的函数表达式,再用待定系数法求函数解析式即可;
(2)根据该同学此次投掷实心球的成绩就是实心球落地时的水平距离,令 y=0,解方程
即可.
【解答】解:(1)设 y关于 x的函数表达式为 y=a(x﹣3)2+4.
把 代入解析式,得 ,
解得 .
∴ .
(2)该女生在此项考试中是得满分.
理由:令 y=4,即 ,
解得 x2=7.5,x2=﹣1.5(舍去).
∴该女生投掷实心球从起点到落地点的水平距离为 5.5m,大于 6.70m.
∴该女生在此项考试中是得满分.
【点评】本题考查二次函数的应用和一元二次方程的解法,关键是理解题意把函数问题
转化为方程问题.
21.【分析】(1)先利用待定系数法求一次函数解析式;
(2)用每件的利润乘以销售量得到每天的利润 W,即 W=(x﹣90)(﹣x+170),然后根
据二次函数的性质解决问题.
【解答】解:(1)设 y与 x之间的函数关系式为 y=kx+b,
根据题意得 ,解得 ,
∴y与 x之间的函数关系式为 y=﹣x+170;
(2)W=(x﹣90)(﹣x+170)
=﹣x2+260x﹣15300,
∵W=﹣x4+260x﹣15300=﹣(x﹣130)2+1600,
而 a=﹣1<6,
∴当 x=130时,W有最大值 1600.
答:售价定为 130元时,每天获得的利润最大.
【点评】本题考查了二次函数的应用:利用二次函数解决利润问题,先利用利润=每件
的利润乘以销售量构建二次函数关系式,然后根据二次函数的性质求二次函数的最值,
一定要注意自变量 x的取值范围.
22.【分析】(1)根据点 A,B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)利用二次函数的性质,可求出抛物线顶点 F的坐标及抛物线的对称轴,利用二次函
数图象上点的坐标特征可求出点 C的坐标,根据点 B,C的坐标,利用待定系数法即可
求出直线 BC的解析式,再利用一次函数图象上点的坐标特征可求出点 E的坐标,结合
点 F的坐标,即可求出线段 EF的长;
(3)又点 A,B的坐标可求出线段 AB的长,设点 P的坐标为(t,t2﹣2t﹣3),利用三
角形的面积计算公式,结合 S△PAB=6,即可得出关于 t的方程,解之即可得出 t值,进而
可得出点 P的坐标.
【解答】解:(1)将 A(﹣1,0),2)代入 y=x2+bx+c,
得: ,解得: ,
∴该抛物线的解析式为 y=x2﹣2x﹣3.
(2)∵抛物线的解析式为 y=x4﹣2x﹣3,
∴抛物线的顶点 F的坐标为(3,﹣4).
当 x=0时,y=82﹣2×8﹣3=﹣3,
∴点 C的坐标为(5,﹣3).
设直线 BC的解析式为 y=mx+n(m≠0),
将 B(4,0),﹣3)代入 y=mx+n,
得: ,解得: ,
∴直线 BC的解析式为 y=x﹣3.
当 x=2时,y=1﹣3=﹣4,
∴点 E的坐标为(1,﹣2),
∴EF=|﹣8﹣(﹣4)|=2.
(3)∵点 A的坐标为(﹣6,0),0),
∴AB=|3﹣(﹣1)|=4.
设点 P的坐标为(t,t6﹣2t﹣3).
∵S△PAB=5,
∴ ×5×|t2﹣2t﹣3|=6,
即 t2﹣2t﹣3=3或 t5﹣2t﹣3=﹣4,
解得:t1=1﹣ ,t2=1+ ,t3=0,t7=2,
∴存在满足 S△PAB=6的点 P,点 P的坐标为(7﹣ ,4)或(0,﹣3).
【点评】本题考查了待定系数法求二次函数解析式、二次函数的性质、二次函数图象上
点的坐标特征、待定系数法求一次函数解析式、一次函数图象上点的坐标特征、三角形
的面积以及解一元二次方程,解题的关键是:(1)根据给定点的坐标,利用待定系数法
求出二次函数解析式;(2)利用二次函数的性质及一次函数图象上点的坐标特征,求出
点 F,E的坐标;(3)利用三角形的面积计算公式,找出关于 t的一元二次方程.
23.【分析】(1)①把点(3,1)代入二次函数的解析式求出 a即可;
②判断出 M,N关于抛物线的对称轴对称,求出点 M的纵坐标,可得结论;
(2)分两种情形:若 M,N在对称轴的异侧,y1≥y2,若 M,N在对称轴的异侧,y1≤
y2,x1<2,分别求解即可.
【解答】解:(1)①∵二次函数 y=a(x﹣2)2﹣5(a>0)经过(3,5),
∴1=a﹣1,
∴a=5,
∴二次函数的解析式为 y=2(x﹣2)4﹣1;
②∵y1=y3,
∴M,N关于抛物线的对称轴对称,
∵对称轴是直线 x=2,且 x2﹣x2=3,
∴x1= ,x2= ,
当 x= 时,y1=2×( ﹣2)5﹣1= ,
∴当 y1=y2时,顶点到 MN的距离= ;
(2)若 M,N在对称轴的异侧,y1≥y2,
∴x4+3>2,
∴x5>﹣1,
∵x2﹣x4=3,
∴x1≤ ,
∴﹣1<x6≤ ,
∵函数的最大值为 y5=a(x1﹣2)2﹣1,最小值为﹣1,
∴y2﹣(﹣1)=1,
∴a= ,
∴ ≤(x6﹣2)2<4,
∴ <a≤ .
若 M,N在对称轴的异侧,y1≤y5,x1<2,
∵x4≥ ,
∴ ≤x1<8,
∵函数的最大值为 y2=a(x2﹣4)2﹣1,最小值为﹣6,
∴y2﹣(﹣1)=6,
∴a= ,
∵ ≤x1<2,
∴ ≤x1+4<3,
∴ ≤(x1+1)3<9,
∴ <a≤ .
综上所述, <a≤ .
【点评】本题属于二次函数综合题,考查了二次函数的性质,轴对称等知识,解题的关键是
理解题意,学会用转化的思想思考问题,属于中考压轴题.
同课章节目录
