【素养进阶单元结构化评价工具】五年级上册第六单元《多边形的面积》整单元作业设计(附:答案版)
文档属性
| 名称 | 【素养进阶单元结构化评价工具】五年级上册第六单元《多边形的面积》整单元作业设计(附:答案版) |  | |
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 19:51:39 | ||
图片预览




文档简介
第 六 单 元 多 边 形 的 面 积
单元评价导语
“多边形的面积”是图形与几何领域“图形的认识与测量”中的重要内容。通过本单元的学习,会计算平行四边形、三角形、梯形的面积,能用相应公式解决实际问题; 会估计不规则图形的面积,形成量感、空间观念和几何直观,提高应用意识和创新意识。
单元知识结构
单元评价目标
090601 通过观察、操作、想象、推理,推导平行四边形、三角形和梯形的面积计算公式,并能正确计算相应图形的面积,了解简单组合图形的面积计算方法,能估测不 规则图形的面积。 量感、空间观念 应用
090602 经历探索平行四边形、三角形和梯形的面积计算公式的推导过程,能条理清楚、有理有据地表达自己的想法,培养观察、比较、推理和概括能力。 推理意识 理解
090603 能用有关图形的面积计算公式解决简单的实际问题,在解决问题的过程中感受数学和现实生活的密切联系,体会学数学、用数学的乐趣。 量感、 几何直观、应用意识、 创新意识 应用、创新
090604 了解数学史,经历古今中外古代数学家的探索过程,感 受数学文化的魅力。在了解数学史、重走数学家探究之路的过程中培养民族自豪感和科学严谨态度。 推理意识、应用意识、创新意识 应用、创新
090605 用自己的方式整理和复习单元所学内容,从多角度理解和沟通多边形面积计算方法之间的联系,灵活运用知识综合解决问题。 几何直观、模型意识、创新意识 应用、分析、创新
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
单元评价内容
第一课时 平行四边形的面积
★基础素养★
【题 1】小维的学校要对花坛边的绿地(平行四边形 A)进行扩建。
右图是扩建设计草图,你能分别算出三个平行四边形 A、B、C 的面积吗?
比一比上述情境中的平行四边形底和高的变化与面积变化的关系,可以用画一画、算一算或列表的方式来分析比较。你也可以再设计新的平行四边形参与比较。
目标序号 090601 核心素养 量感(水平三) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 创编
设计意图 通过读图,会计算平行四边形的面积;通过观察和计算比较出三个平行四边形对应的底与高的变化与面积变化的关系, 进一步理解平行四边形的底和高与面积之间的关系。
★能力素养★
【题 2】如图,把一些练习本摞成一个长方体,长方体的前面是一个长方形,再把这摞练习本均匀地斜放(如图),这时前面变成了一个近似的平行四边形。小维说长方形和平行四边形的周长和面积都没有发生变化。
小维的观点有道理吗?为什么?
小思想实际算算这个近似平行四边形的面积,她测量了相关数据:两条邻边分别长 6cm 和 18.6cm,再从一个顶点出发,量得垂直于两条底边的高是分别 5cm 和 15.5cm,接着画出了示意图,这个平行四边形的面积是多少平方厘米?
以下有 4 个可能出现的答案,哪个答案是正确的 (
A.30 B.93 C.111.6 D.77.5
选择一个错误答案说说有可能出现这种错误的原因是什么?给你什么启示?
目标序号 090603 核心素养 几何直观(水平三) 认知维度 应用
预估难度 易 预估时长 8 分钟 设计方式 创编
设计意图 在现实情境中辨别平行四边形的周长和面积 ,在变 与不变中理解平行四边形面积的本质 ,有效 沟通平行四边形面积计算与长方形面积计算之间的内在联系 ,深度 理解平行四边形面积 的意义。
★综合应用★
(
0
图
1
)【题 3】平行四边形不是轴对称图形,而是中心对称图形, 因为平行四边形绕着对角线交点 O 旋转 180°后,能够和原来图形位置重合(如图 1),因此,平行四边形是以对角线交点O 为对称中心的中心对称图形。
你能解决这个问题吗?请你独立或者“组团”完成这个任务,并将“设计方案、探索尝试、形成结论、解决问题”的过程记录下来,完成《探究任务单》。
探究任务单 探究者:
任务 F 通过 F 点,用一条线段将平行四边形分成面积相等的两部分。
方案设计
探究过程
形成结论
问题解决
完成探究任务了,对自己或请老师和同学给自己做出评价吧!
目标序号 090603 核心素养 创新意识(水平二) 认知维度 创新
预估难度 难 预估时长 30 分钟 设计方式 创编
设计意图 创设探究性问题情境,让学生通过合作、探究、体验, 融合学科知识解决生活中的数学问题 ,使学 科知识在探究活动中得到延伸和发展,增强学生的动手操作能力,提升团结协作意 识, 创新数学思维, 提升学科核心素养。
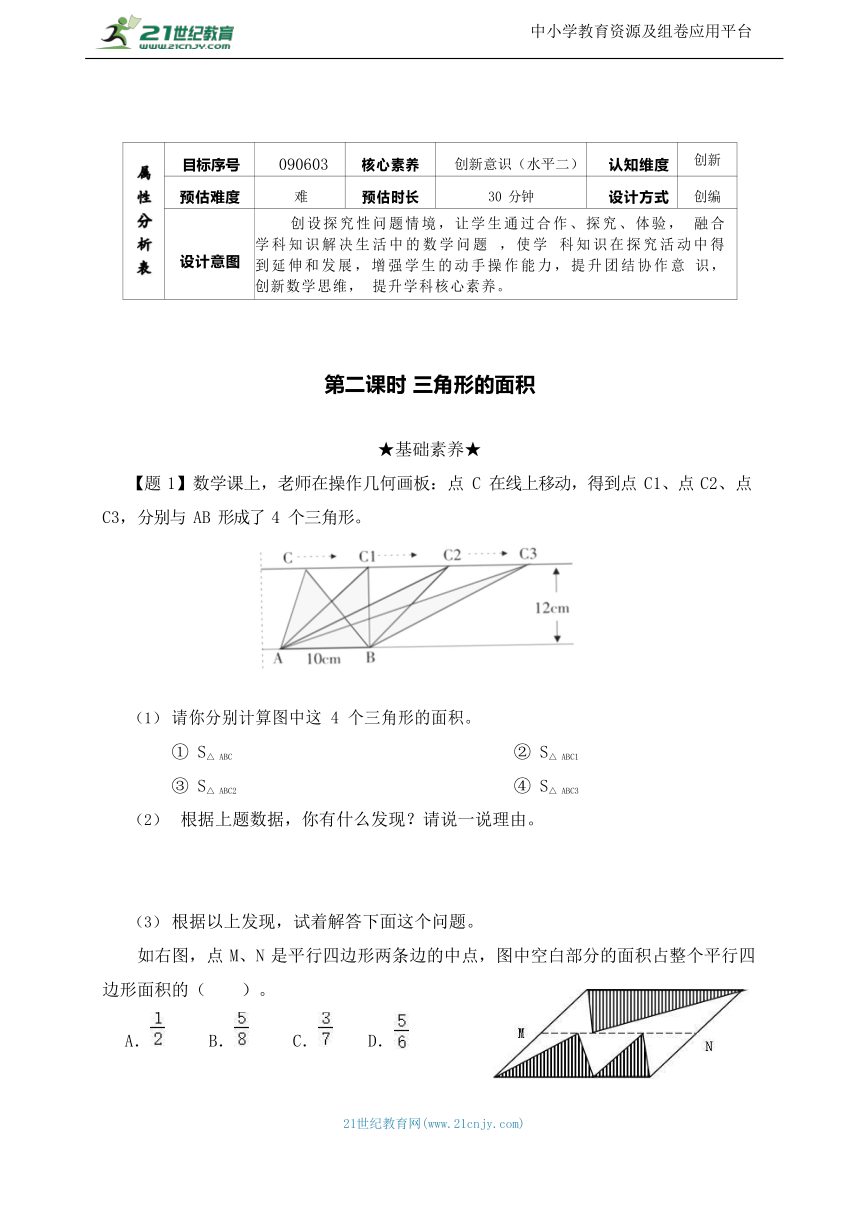
第二课时 三角形的面积
★基础素养★
【题 1】数学课上,老师在操作几何画板:点 C 在线上移动,得到点 C1、点 C2、点C3,分别与 AB 形成了 4 个三角形。
请你分别计算图中这 4 个三角形的面积。
① S△ ABC ② S△ ABC1
③ S△ ABC2 ④ S△ ABC3
根据上题数据,你有什么发现?请说一说理由。
根据以上发现,试着解答下面这个问题。
如右图,点 M、N 是平行四边形两条边的中点,图中空白部分的面积占整个平行四边形面积的( )。
A. B. C. D.
目标序号 090601 核心素养 推理意识(水平一) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 改编
设计意图 通过题组, 引导学生观察点 C 在两平行线间的线上移动, 利用三角形的底和高计算面积并比较大小 ,进而 理解三角形的面积取决于它的底和高, 与形状无关, 提升学生的思维能力。
★能力素养★
【题 2】某水田种植基地的稻田如右图所示。
每平方千米能产水稻 750 吨,预计总产量为多少吨?
(
稻田
)1.4km
2.5km
若将这块稻田进行扩建,使得面积为原来的 2 倍,下面第( )号方案的设计符合要求,并请你也设计一个方案,使得面积为原来稻田的 2 倍,但形状不一样哦!
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 5 分钟 设计方式 改编
设计意图 考查学生是否能熟练的掌握三角形面积的计算公式 ,并解决简单的实际问题,发展数学应用意识。通过将这块稻田进行 扩建,使得面积为原来的 2 倍,让学生在图形的变化中体验体 会图形各个元素与面积之间的关系, 拓展学生思维能力。
【题 3】根据全国少工委 2005 年颁发的《关于中国少年先锋队队旗、队徽和红领巾、队干部标志制作和使用的若干规定》,少先队员佩戴的红领巾分大、小号两种规格。
规格一:等腰三角形,底长为 100 厘米,腰为 60 厘米。
规格二:等腰三角形,底长为 120 厘米,腰为 72 厘米。
(1)育才小学选用小号规格的红领巾(如图),这条红领巾的面积是多少?
(
60cm
)100cm
(2)10m2 的布最多能做多少条这种规格的红领巾?
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 5 分钟 设计方式 选编
设计意图 利用小号规格红领巾的数据 ,熟练 地运用三角形面积计算公式解决问题; 通过 “ 10m 2 的布最多能做多少条这种规格的 红领巾? ”这个 具有开放性的问题引发思考 ,激发 思维的碰撞, 拓展解决问题的思路。
★综合应用★
【题 4】我国古代数学名著《九章算术》中称三角形为圭田,面积公式为“术曰:半广以乘正从(音纵 zong)”。这里广是指三角形的底边,正从是指底边上的高,也就是“三角形面积=三角形的底边的一半×底边上的高”。(如图 1)
图 1 图 2
刘徽在注文中对这一计算公式实质上作了证明:“半广者,以盈补虚,为直田也。” “亦可以半正从以乘广”(如图 2)。盈是多余,虚乃不足。“以盈补虚”就是以多余部分填补不足的部分,这就是我国古代数学推导平面图形面积公式所用的传统的“出入相补”的方法,由上图“以盈补虚”变圭田为与之等积的直田,于是得到了圭田的面积计算公式。
你读懂了吗?试一试:
如果用上述“以盈补虚”的转化方法将下图三角形转化成长方形,已知长方形 DBCE 的面积为 180 平方厘米,图中 F、G 均为三角形两边的中点,你知道三角形 ABC 的高吗?
目标序号 090602 核心素养 推理意识(水平三) 认知维度 理解
预估难度 中 预估时长 8 分钟 设计方式 改编
设计意图 考查学生掌握三角形面积的推导过程。通过观察图形,运 用“ 出入相补”原理理解三角形面积公式的本质,渗透转化思想。通过数学史料的学习,在了解数学史、重走数学家探究之 路, 培养民族自豪感。
第三课时 梯形的面积
★基础素养★
【题 1】如图是一张破损的等腰梯形纸片,破损前这张梯形纸片的面积是多少? 反思一下自己的解答,确定吗? 10
8
6 单位:厘米
目标序号 090601 核心素养 空间观念(水平一) 认知维度 理解
预估难度 易 预估时长 3 分钟 设计方式 改编
设计意图 通过观察图形,能根据给出的信息找到计算梯形面积的必需条件;能够 根据等腰梯形的特征,反思解决问题的方法。
★能力素养★
【题 2】一辆汽车侧面车窗前后两块玻璃的形状近似梯形(如图),这两块玻璃哪块面积大?(请写出你的思考过程)
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 易 预估时长 5 分钟 设计方式 改编
设计意图 考查学生能否灵活运用梯形面积计算公式解决简单的生活实际问题。这题有多种解题方法,可以通过计算解决,也可 以结合图形的特征及元素的关系综合思考解题思路 ,可以 考查不同思维倾向和思维层次的学生的想法 ,提高 对梯形面积计算 的本质理解。
【题 3】学校“研学”基地用 65 米长的竹篱笆,靠墙边围成了一块直角梯形的瓜地
(如图 1)。
这块瓜地的面积是多少平方米?
如果增加篱笆(如图 2),把瓜地变成平行四边形的形状,那么瓜地就增加 75m2(图中空白部分),求原来梯形瓜地的下底长是多少米?
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 7 分钟 设计方式 改编
设计意图 本题考查学生能否灵活运用梯形、三角形、平行四边形面积计算方法解决生活中的简单实际问题 。学生 通过分析平面图形的性质 ,沟通 了平行四边形 、三角 形和梯形面积之间的联系, 进一步提高解决问题的能力。
★综合应用★
【题 4】《九章算术注》同样记载了运用“出入相补”原理对邪田(直角梯形)和箕田(梯形)的面积公式推导。
小思也尝试运用“出入相补”原理推导任意梯形 ABCD 的面积。(下图所示)你能理解她的方法吗?在下面正确的说法前面打“√”。
A D
( )拼成一个和梯形面积相等的长方形
( )长方形的宽与梯形的高相等 E F
( )长方形的长是梯形上底与下底之和的一半
( )梯形的面积=(上底+下底)÷2×高 B C
目标序号 090604 核心素养 推理意识(水平二) 认知维度 应用
预估难度 中 预估时长 5 分钟 设计方式 创编
设计意图 考查学生能否在理解梯形面积计算推导的基础上 ,独立 自主探究不一样的推导方法。 通过观察图形, 思考“ 出入相补” 原理,理解面积计算公式的本质,渗透转化思想,并通过学习我国古代数学家的方法, 感受数学文化的魅力。
第四课时 组合图形的面积
★基础素养★
【题 1】学习小组正在研究怎样计算组合图形的面积。
12 m
(
4m
)10 m
15m
(1)你能看懂小维和小思的方法吗?请在图中画一画,并说一说你是怎么想的。
(
我是这样算的:
12×4
+(
12+15
)
×6÷2
12 m
)
(
我是这样算的:
(
12+15
)
×10÷2
-
4×3÷2
12
m
4m
10
m
) (
4m
)10 m
15m
把图形分割成( )形和( )形。
15m
补上一个( )形,把图形转化成一个( )形。
(2)你还有不一样的计算方法吗?请在图中画出辅助线并列式计算。
12 m
(
4m
)10m
15m
(
比较一下大家不同的计算方法,你有
什么新的收获?
)
目标序号 090601 核心素养 空间观念(水平三) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 创编
设计意图 结合图形和算式,引导学生进行分割和说理,从正向思维和逆向思维两 个角度考查学生对组合图形面积计算的掌握情况,进一步理解组合图形的面 积计算的思考过程和具体的计算方法,发展空间观念。
★能力素养★
【题 2】我们日常使用的口罩呈长方形,尺寸如图 1。为便于佩戴时展开,口罩加工时中间要做三条折叠,每条折叠折进的宽度为 1cm(图 2 中B点到C点的长度)。制作 这个口罩,至少需要多少布料?(图 2 中F点和H点重合)
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 易 预估时长 5 分钟 设计方式 选编
设计意图 运用组合图形出入相补原理 ,将口 罩折叠的面积转化成长方形的面积,再选择合理的方法解决问题,体会解决问题的方 法和策略的多样性,培养分析、解决问题的能力,感受数学与 生活的密切联系。
★综合应用★
【题 3】明代戈汕著的《蝶几图》是中国古代组合家具的设计图。“几”指的是桌型器具,“蝶几”的桌面有 6 种基本形状,共 13 张,可以根据需要自由组合,蝶
几图中共计列出了 8 类 76 种不同图案形状的组合桌。
下图就是一套“蝶几”模型的平面设计图(每格长 1dm)。
《蝶几图》中有一种拼组好的桌面,名为“葵实”,形状如图。这张“葵实” 桌面的面积是 dm2。
“葵实”可以由哪几种基本形状的桌面拼组成,把你的拼组方案画在图中。( 注意每种基本形状桌面的张数。)
目标序号 090604 核心素养 应用意识(水平二) 创新意识(水平二) 认知维度 应用
预估难度 中 预估时长 8 分钟 设计方式 选编
设计意图 通过阅读数学材料,进行数学文化、数学思想的渗透,同 时考查梯形面积公式的灵活运用。认识《 蝶几图》的基本图形及拼组方法,吸取知识的同时发展数学思维。通过渗透数学文 化开阔视野, 增强数学学习的兴趣。
第五课时 不规则图形的面积
★基础素养★
【题 1】小朋友刚出生,就有了第一个身份的证明“足印”。
下面是小思刚出生时的足印,这个足印大约有多大呢?请你把解决问题的思路和结果写出来。(下图中每个小方格的面积是 1cm2)
方法一:
方法二:
比较一下这两种估测的结果,差距大吗?想想有可能是什么原因?
目标序号 090601 核心素养 量感(水平三) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 创编
设计意图 能熟练运用数方格和转化为近似的规则图形的方法估测不规则图形的 面积,体会估算策略和方法的多样性和差异性,进一步发展量感。
★能力素养★
【题 2】小维和同学们在研究一棵树一年大约能吸收多少克二氧化碳。
先捡一片大小中等的落叶,测量它的面积。
以下是 3 位同学测量的过程,他们估测的结果分别是多少?
约( )cm2 约( )cm2 约( )cm2
比较三人的估测结果,你有什么想说的?你认为谁估计的结果更准确些?为什么?
假如每平方米树叶每天能吸收约 5 克二氧化碳,一棵树有 10000 片这样的树叶,
那么这棵树一年(按 365 天计算)大约能吸收多少克二氧化碳?
目标序号 090603 核心素养 量感(水平三) 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 7 分钟 设计方式 改编
设计意图 运用不同方格测量同一物体的面积 ,进行 直观的估测和比较,感悟估测范围与结果随测量单位变小而越来越准确,发展 学生的空间观念和量感, 积累数学活动经验。
★综合应用★
【题 3】在我们熟悉的方格图中,每一组横纵线的交点就叫做一个格点,以格点为顶点画出的多边形叫做“格点多边形”。
“格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能用计算公式来表达吗?”
(
多边形面积
=
内部点数
+
边线点数
÷
2-1
)数学家毕克多年研究格点多边形的面积,终于找到了格点数目与图形面积的关系, 近似证明得出“毕克”定理:顶点都在正方形格点上的多边形,如下图,内部点(绿色) 点数直接计入面积,边线点(紫色和红色)点数除以 2 后,再减 1,所以得到
(1)根据这段话的描述,你能算出图 1 中的多边形的面积吗?
图 1 图 2
用我们学习估算多边形面积的方法在图 2 中验证一下。
你觉得格点多边形面积有趣吗?在右边的方格纸上设计一个多边形,并算算它的面积吧!(内部点用○表示,边线点用●表示)
目标序号 090604 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 8 分钟 设计方式 创编
设计意图 通过阅读相关材料,拓展数学文化,丰富多边形面积的估 测方法,知识获得的同时经历了阅读理解、尝试运用、验证检 查、 内化应用的过程, 培养学生数学阅读能力和应用意识。
单元素养作业
★知识地图★
学习了这个单元,你能整理本单元的学习内容吗?可以用文字、表格或思维导图, 也可以是其他你喜欢的方式,试试看吧!完成之后可以和小伙伴互相交流,进一步完善整理的内容。
目标序号 090605 核心素养 创新意识 认知维度 创新
预估难度 中 预估时长 10 分钟 设计方式 创编
设计意图 激发学生对本单元所学习内容的深层次的思考,通过整理突出核心知识, 建立知识之间的联系,体现知识内在的逻辑关系;通过文字、表格或思维导图 使核心内容可视化、结构化,进一步把握知识脉络,形成整体、全面的认识。
★基础素养★
(
2cm
6cm
8cm
)【题 1】小维的学校要建一面艺术墙(如图所示),要给这面墙
刷一层底漆,要刷的面积有多大? (1)用分割的方法算一算:
(
我把图形分割成
2cm
6cm
8cm
)
①
(
我把图形分割成
2cm
6cm
8cm
)
②
下面这 4 种方法可以计算墙面的面积吗?试着说一说理由。
(
可以动手剪一剪,拼一拼。
)
③ ④ ⑤ ⑥
( ) ( ) ( ) ( )
你能看懂他们的方法吗?试着画图并简要说明。
(
2cm
6cm
8cm
) (
2cm
6cm
8cm
)小芳是这样算的:8×8-(8÷2)×2÷2×2 小明是这样算的:(6+8)×8÷2
⑦ ⑧
如果要给这些方法分分类,可以怎样分类?试着分一分、写一写。
目标序号 090605 核心素养 几何直观(水平三) 认知维度 分析
预估难度 中 预估时长 8 分钟 设计方式 创编
设计意图 运用等积变换的思想,用分割法、割补法、添补法、等积变形法把组合 图形转化成已学过的图形来计算面积,培养学生空间想象能力,通过分类, 进一步沟通不同的转化方法之间的联系,数形结合,建立不同方法的模型。
★能力素养★
【题 2】(1) 星期六,小思和小维在研究数学问题。
A点往左平移( )格变成( ) 形,如果用梯形面积公式计算它的面积:
A点往右平移到与B点重合变成( ) 形,如果用梯形面积公式计算它的面积:
通过计算,你有什么发现?
(2)星期天,小维与爸爸来到木材厂,看到一堆木头,如图。聪明的小维运用数学知识,列出了算式:
(3+6)×4÷2
他很快算出了木头的数量,他的这种计算方法其实是( + )×层数÷2。这是什么道理呢?
(3)爸爸给小维提了一个问题:“你能用刚才的方法来计算下面算式的和吗?” 1+2+3+4+5+……+98+99+100=
你能帮助小维解决这个问题吗?请写出思考过程。
目标序号 090605 核心素养 几何直观(水平三) 模型意识(水平三) 认知维度 分析
预估难度 中 预估时长 10 分钟 设计方式 创编
设计意图 沟通各平面图形面积计算之间的联系 ,理解 梯形面积公式作为“ 通用公式”的含义,以及它在实际生活中的应用,将图形的面积计算、等差数列等内容综合考查,数形结合,提高学 生的模型意识。
★综合应用★
【题 3】《九章算术》方田章主要论述平面图形直线形和圆的面积计算方法。其中第一题“今有田广十五步,从(音纵 zong)十六步。问为田几何。”“答曰:一亩”。这里“广”就是宽,“从”即纵,指其长度,“方田术”曰:广从步数相乘得积步(得积
步就是得到乘积的平方步数)。意思就是一块长方形的田地,宽边是十五步,长边是十六步,这块田的面积就是一亩。
请在图中画出面积约为一亩的图形。(如图 1 方格图所示:正方形小格的边长表示一步长)
(图 1)
王大爷要把一块梯形的田,平均分给三个儿子,每个儿子分得几亩田?(如图2 所示:正方形小格的边长表示一步长)
(图 2)
请帮王大爷在图 2 中将田平均分一分,分成面积相等的三份。
目标序号 090605 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 8 分钟 设计方式 创编
设计意图 通过了解古人测量和计量土地面积的方法, 考查长方形、梯形面积公式的灵活运用,利用数方格、计算公式等多边形面积计算的方法,增强学生学习的兴趣、开阔视野,提高文化素养和应用能力。
评价工具答案解析
【题 1】
第一课时 《平行四边形的面积》答案解析
(1)A: 6×5=30(cm2) B: 12×10=120(cm2) C:24×20=480(cm2)
(2)(答案不唯一)如:
图形 A B C
底 6cm 12cm 24cm
高 5cm 10cm 20cm
面积 30cm2 120cm2 480cm2
发现:平行四边形的底和高同时扩大为原来的 2 倍,面积扩大到原来的 4 倍。
【题 2】
(1)小维的观点不对,因为书本摆成的长方形变成平行四边形后边长变了,周长也变大了,但是高不变,所以面积也不变。
(2)( B)
A:6×118.6=111.6 用了平行四边形的两条邻边相乘,所以是错误的。B:5×15.5=77.5,用了平行四边形的两条高相乘,所以是错的。 C:5×6=30,用了平行四边形的一条边和不对应的一条高相乘,所以是错的。
启示:计算平行四边形的面积要采用底和高对应的数据。
【题 3】
探究性学习指导意见:
鼓励学生独立自主探究,遇到困难可寻求同学、老师或家长的帮助和指导。
鼓励学生以小组为学习单位合作学习,相互交流、合作探究。
在探究活动中,可以对有困难的学生提供帮扶,对学有余力的学生给予指导,确保学生在课后规定的时间内完成。
采用多样化得评价方式,关注学生探究态度、探究能力和合作学习能力得提升。
第二课时 《三角形的面积》答案解析
【题 1】
(
△ ABC
△
ABC1
)(1)① S =10×12÷2=60 (cm2) ② S =10×12÷2=60 (cm2)
(
△ ABC2
△
ABC3
)③ S = 10×12÷2=60 (cm2) ④ S =10×12÷2=60 (cm2)
(2)(答案不唯一)我发现了:这四个三角形的面积相等,因为他们都等底等高,所以面积相等。
(3) A
【题 2】
(1)1.4×2.5÷2×750=1312.5(吨)
(2)( ③ ) 画图(答案不唯一)
【题 3】
(1)100×33÷2=1650(cm2)
(2)假设 10m2 的布是长 10m,宽是 1m 的长方形。(可以画示意图) 10m=1000cm 1m=100cm
1000÷100=10(个) 100÷33=3(组)
10+(10-1)=19(个) 19×3=57(条)
【题 4】
180÷30×2=12(cm)或者 180×2÷30=12(cm)
第三课时 《梯形的面积》答案解析
【题 1】(方法不唯一)
[10+(6×2+10)]×8÷2=128(cm2)
反思:梯形的下底=三角形的底×2+上底,再根据梯形面积公式计算面积,答案正确。
【题 2】前窗玻璃面积大(方法不唯一) 方法一:
(40+71)×40÷2=2220(cm2) (45+65)×40÷2=2200(cm2) 2220>2200
方法二:
两个梯形的高相等,只要比较它们的两底之和 。
40+71=111(m) 45+65=110(m) 111>110
方法三:
比较梯形的各部分组成元素,即分别比较两个梯形的高、上底、下底,得到差值, 也可以比较出面积的大小。
【题 3】
(1)(65-25)×25÷2=500(m2)
(2)方法一:(500+75)÷25=23(m) 方法二: 75×2÷25=6(m)
(65-25+6)÷2=23(m)
【题 4】
( √ )拼成一个面积相等的长方形
( √ )长方形的宽与梯形的高相等
( √ )长方形的长是梯形上底与下底之和的一半
( √ )梯形的面积=(上底+下底)÷2×高
第四课时 《组合图形的面积》答案解析
【题 1】
(1) 长方 梯 三角 梯
(2)(答案不唯一)
预设:12×4+15×6÷2 12×3+3×6÷2 15×10-(4+10)×3÷2
收获:计算组合图形的面积时,可以用分割法或割补法进行计算。
【题 2】
分析:
这个口罩展开后的面积也就是长为 18 厘米,宽为(4+1×2×3+1×2+3)厘米的长方形的面积,长方形的面积=长×宽,代入即可。
方法一:18×(4+1×2×3+1×2+3)=270(cm2)
方法二:18×1×8=144(cm2) 18×4=72(cm2) 18×3=54(cm2) 144+72+54=270(cm2)
【题 3】
分析:通过观察图形可知,把拼组好的桌面分成两个完全一样的图形,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。(2+6)×2÷2×2=16(平方分米)
分析:根据“几”的基本图形可知,这个“葵实”可以由“左半斜”一张,“右半斜”一张,“ 小三斜”一张拼组成。作图如下:
或由“左半斜”一张(“右半斜”一张),“小三斜”一张,“闰”一张拼组成的。作图如
下:
第五课时 《不规则图形的面积》答案解析
【题 1】
方法一:我用数方格的方法,满格的有 5 格,就是 5cm2,不满格的有 16 格,都按半格算,所以足印的面积:5+16÷2=13(cm2)
方法二:我把足印转化成近似的梯形,如图,梯形的上底是 4 厘米,下底是 2 厘米,高是 5 厘米,所以足印的面积大约是:(4+2)×5÷2=15(cm2)
这两种估测的结果差距不大。估测都会有一些差距,因为估测时选择的方法不一样, 得到的数据就会不一样,结果也就不一样。但在估测时,不管用数方格的方法,还是转化成近似的规则图形,都应该尽量做到接近准确,所以差距不大。(分析原因的答案不唯一,合理即可。)
【题 2】
(1) 约(36)cm2 约(34)cm2 约(29)cm2
(2)三人所用的测量方格纸的规则不一样,第一人用的一格是 9cm2 的方格纸,第二人用的是 4cm2 的方格纸,第三人用的是 1cm2 的方格纸,所以他们侧量的结果也不一样,随着方格的大小逐渐变小,估测出来的结果也逐渐变小。
我认为第三人的估测结果更准确。因为,它的格子的边长最小,所以测量得的结果最接近准确值。
(3) 29cm2=0.29dm2=0.0029m2 0.0029×10000×5×365
=29×5×365
=145×365
=52925(克)
【题 3】
(1)39+14÷2-1=45(cm2)
(2) 如下图,我把多边形转化成一个近似的梯形,梯形的上底是 8 厘米,下底是 7 厘
米,高是 6 厘米,所以这个多边形的面积大约是:(8+7)×6÷2=45(cm2)
(答案不唯一,结果在 45cm2 左右,算式或过程合理均对)
(3)答案略,答案不唯一。
单元素养作业
【题 1】
分割法:① 分割成 1 个三角形和一个长方形
8×2÷2+8×6=56(cm2)
② 分割成 2 个完全相同的梯形(6+8)×(8÷2)÷2×2=56(cm2)
(2)( √ ) ( √ ) ( √ ) (√ ) 割补法: ③ 转化成一个大长方形和小长方形
8×6+(8÷2)×2=56(cm2)
④ 转化成一个长方形
(8+6)× (8÷2)=56(cm2)
⑤ 转化成一个平行四边形
(8+6)× (8÷2)=56(cm2)
⑥ 转化成一个梯形
(6+6+8+8)×(8÷2)÷2=56(cm2)
(3)小芳:
添补法:⑦ 添补成一个正方形,再减去多算的 2 个三角形的面积
8×8-(8÷2)×2÷2×2=56(cm2)
小明:
等积变形法:⑧ 根据“2 个等底等高的三角形面积相等”,转化成一个梯形
(6+8)×8÷2=56(cm2)
(4) 分割法:①②②
割补法:③④⑤⑥ 添补法:⑦
等积变形法:⑧
【题 2】
(1)3,平行四边,(5+5)×2÷2=10,三角,(0+5)×2÷2=5
发现:运用梯形的面积计算公式也可以算出其他图形的面积,可以说它是一个“万能公式”。
上层根数,下层根数。学生能够用梯形面积计算公式去说明理由,合理即可。
学生可以通过画图、计算进行说理。
【题 3】
(1)16×15=240(平方步)
240 平方步=1 亩 (图略)
(2)(24+48)×20÷2÷240÷3=1(亩)
(3)因为梯形的下底是上底的 2 倍,所以把这个梯形分成等底等高的 3 个三角形即可。
单元评价导语
“多边形的面积”是图形与几何领域“图形的认识与测量”中的重要内容。通过本单元的学习,会计算平行四边形、三角形、梯形的面积,能用相应公式解决实际问题; 会估计不规则图形的面积,形成量感、空间观念和几何直观,提高应用意识和创新意识。
单元知识结构
单元评价目标
090601 通过观察、操作、想象、推理,推导平行四边形、三角形和梯形的面积计算公式,并能正确计算相应图形的面积,了解简单组合图形的面积计算方法,能估测不 规则图形的面积。 量感、空间观念 应用
090602 经历探索平行四边形、三角形和梯形的面积计算公式的推导过程,能条理清楚、有理有据地表达自己的想法,培养观察、比较、推理和概括能力。 推理意识 理解
090603 能用有关图形的面积计算公式解决简单的实际问题,在解决问题的过程中感受数学和现实生活的密切联系,体会学数学、用数学的乐趣。 量感、 几何直观、应用意识、 创新意识 应用、创新
090604 了解数学史,经历古今中外古代数学家的探索过程,感 受数学文化的魅力。在了解数学史、重走数学家探究之路的过程中培养民族自豪感和科学严谨态度。 推理意识、应用意识、创新意识 应用、创新
090605 用自己的方式整理和复习单元所学内容,从多角度理解和沟通多边形面积计算方法之间的联系,灵活运用知识综合解决问题。 几何直观、模型意识、创新意识 应用、分析、创新
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
单元评价内容
第一课时 平行四边形的面积
★基础素养★
【题 1】小维的学校要对花坛边的绿地(平行四边形 A)进行扩建。
右图是扩建设计草图,你能分别算出三个平行四边形 A、B、C 的面积吗?
比一比上述情境中的平行四边形底和高的变化与面积变化的关系,可以用画一画、算一算或列表的方式来分析比较。你也可以再设计新的平行四边形参与比较。
目标序号 090601 核心素养 量感(水平三) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 创编
设计意图 通过读图,会计算平行四边形的面积;通过观察和计算比较出三个平行四边形对应的底与高的变化与面积变化的关系, 进一步理解平行四边形的底和高与面积之间的关系。
★能力素养★
【题 2】如图,把一些练习本摞成一个长方体,长方体的前面是一个长方形,再把这摞练习本均匀地斜放(如图),这时前面变成了一个近似的平行四边形。小维说长方形和平行四边形的周长和面积都没有发生变化。
小维的观点有道理吗?为什么?
小思想实际算算这个近似平行四边形的面积,她测量了相关数据:两条邻边分别长 6cm 和 18.6cm,再从一个顶点出发,量得垂直于两条底边的高是分别 5cm 和 15.5cm,接着画出了示意图,这个平行四边形的面积是多少平方厘米?
以下有 4 个可能出现的答案,哪个答案是正确的 (
A.30 B.93 C.111.6 D.77.5
选择一个错误答案说说有可能出现这种错误的原因是什么?给你什么启示?
目标序号 090603 核心素养 几何直观(水平三) 认知维度 应用
预估难度 易 预估时长 8 分钟 设计方式 创编
设计意图 在现实情境中辨别平行四边形的周长和面积 ,在变 与不变中理解平行四边形面积的本质 ,有效 沟通平行四边形面积计算与长方形面积计算之间的内在联系 ,深度 理解平行四边形面积 的意义。
★综合应用★
(
0
图
1
)【题 3】平行四边形不是轴对称图形,而是中心对称图形, 因为平行四边形绕着对角线交点 O 旋转 180°后,能够和原来图形位置重合(如图 1),因此,平行四边形是以对角线交点O 为对称中心的中心对称图形。
你能解决这个问题吗?请你独立或者“组团”完成这个任务,并将“设计方案、探索尝试、形成结论、解决问题”的过程记录下来,完成《探究任务单》。
探究任务单 探究者:
任务 F 通过 F 点,用一条线段将平行四边形分成面积相等的两部分。
方案设计
探究过程
形成结论
问题解决
完成探究任务了,对自己或请老师和同学给自己做出评价吧!
目标序号 090603 核心素养 创新意识(水平二) 认知维度 创新
预估难度 难 预估时长 30 分钟 设计方式 创编
设计意图 创设探究性问题情境,让学生通过合作、探究、体验, 融合学科知识解决生活中的数学问题 ,使学 科知识在探究活动中得到延伸和发展,增强学生的动手操作能力,提升团结协作意 识, 创新数学思维, 提升学科核心素养。
第二课时 三角形的面积
★基础素养★
【题 1】数学课上,老师在操作几何画板:点 C 在线上移动,得到点 C1、点 C2、点C3,分别与 AB 形成了 4 个三角形。
请你分别计算图中这 4 个三角形的面积。
① S△ ABC ② S△ ABC1
③ S△ ABC2 ④ S△ ABC3
根据上题数据,你有什么发现?请说一说理由。
根据以上发现,试着解答下面这个问题。
如右图,点 M、N 是平行四边形两条边的中点,图中空白部分的面积占整个平行四边形面积的( )。
A. B. C. D.
目标序号 090601 核心素养 推理意识(水平一) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 改编
设计意图 通过题组, 引导学生观察点 C 在两平行线间的线上移动, 利用三角形的底和高计算面积并比较大小 ,进而 理解三角形的面积取决于它的底和高, 与形状无关, 提升学生的思维能力。
★能力素养★
【题 2】某水田种植基地的稻田如右图所示。
每平方千米能产水稻 750 吨,预计总产量为多少吨?
(
稻田
)1.4km
2.5km
若将这块稻田进行扩建,使得面积为原来的 2 倍,下面第( )号方案的设计符合要求,并请你也设计一个方案,使得面积为原来稻田的 2 倍,但形状不一样哦!
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 5 分钟 设计方式 改编
设计意图 考查学生是否能熟练的掌握三角形面积的计算公式 ,并解决简单的实际问题,发展数学应用意识。通过将这块稻田进行 扩建,使得面积为原来的 2 倍,让学生在图形的变化中体验体 会图形各个元素与面积之间的关系, 拓展学生思维能力。
【题 3】根据全国少工委 2005 年颁发的《关于中国少年先锋队队旗、队徽和红领巾、队干部标志制作和使用的若干规定》,少先队员佩戴的红领巾分大、小号两种规格。
规格一:等腰三角形,底长为 100 厘米,腰为 60 厘米。
规格二:等腰三角形,底长为 120 厘米,腰为 72 厘米。
(1)育才小学选用小号规格的红领巾(如图),这条红领巾的面积是多少?
(
60cm
)100cm
(2)10m2 的布最多能做多少条这种规格的红领巾?
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 5 分钟 设计方式 选编
设计意图 利用小号规格红领巾的数据 ,熟练 地运用三角形面积计算公式解决问题; 通过 “ 10m 2 的布最多能做多少条这种规格的 红领巾? ”这个 具有开放性的问题引发思考 ,激发 思维的碰撞, 拓展解决问题的思路。
★综合应用★
【题 4】我国古代数学名著《九章算术》中称三角形为圭田,面积公式为“术曰:半广以乘正从(音纵 zong)”。这里广是指三角形的底边,正从是指底边上的高,也就是“三角形面积=三角形的底边的一半×底边上的高”。(如图 1)
图 1 图 2
刘徽在注文中对这一计算公式实质上作了证明:“半广者,以盈补虚,为直田也。” “亦可以半正从以乘广”(如图 2)。盈是多余,虚乃不足。“以盈补虚”就是以多余部分填补不足的部分,这就是我国古代数学推导平面图形面积公式所用的传统的“出入相补”的方法,由上图“以盈补虚”变圭田为与之等积的直田,于是得到了圭田的面积计算公式。
你读懂了吗?试一试:
如果用上述“以盈补虚”的转化方法将下图三角形转化成长方形,已知长方形 DBCE 的面积为 180 平方厘米,图中 F、G 均为三角形两边的中点,你知道三角形 ABC 的高吗?
目标序号 090602 核心素养 推理意识(水平三) 认知维度 理解
预估难度 中 预估时长 8 分钟 设计方式 改编
设计意图 考查学生掌握三角形面积的推导过程。通过观察图形,运 用“ 出入相补”原理理解三角形面积公式的本质,渗透转化思想。通过数学史料的学习,在了解数学史、重走数学家探究之 路, 培养民族自豪感。
第三课时 梯形的面积
★基础素养★
【题 1】如图是一张破损的等腰梯形纸片,破损前这张梯形纸片的面积是多少? 反思一下自己的解答,确定吗? 10
8
6 单位:厘米
目标序号 090601 核心素养 空间观念(水平一) 认知维度 理解
预估难度 易 预估时长 3 分钟 设计方式 改编
设计意图 通过观察图形,能根据给出的信息找到计算梯形面积的必需条件;能够 根据等腰梯形的特征,反思解决问题的方法。
★能力素养★
【题 2】一辆汽车侧面车窗前后两块玻璃的形状近似梯形(如图),这两块玻璃哪块面积大?(请写出你的思考过程)
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 易 预估时长 5 分钟 设计方式 改编
设计意图 考查学生能否灵活运用梯形面积计算公式解决简单的生活实际问题。这题有多种解题方法,可以通过计算解决,也可 以结合图形的特征及元素的关系综合思考解题思路 ,可以 考查不同思维倾向和思维层次的学生的想法 ,提高 对梯形面积计算 的本质理解。
【题 3】学校“研学”基地用 65 米长的竹篱笆,靠墙边围成了一块直角梯形的瓜地
(如图 1)。
这块瓜地的面积是多少平方米?
如果增加篱笆(如图 2),把瓜地变成平行四边形的形状,那么瓜地就增加 75m2(图中空白部分),求原来梯形瓜地的下底长是多少米?
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 7 分钟 设计方式 改编
设计意图 本题考查学生能否灵活运用梯形、三角形、平行四边形面积计算方法解决生活中的简单实际问题 。学生 通过分析平面图形的性质 ,沟通 了平行四边形 、三角 形和梯形面积之间的联系, 进一步提高解决问题的能力。
★综合应用★
【题 4】《九章算术注》同样记载了运用“出入相补”原理对邪田(直角梯形)和箕田(梯形)的面积公式推导。
小思也尝试运用“出入相补”原理推导任意梯形 ABCD 的面积。(下图所示)你能理解她的方法吗?在下面正确的说法前面打“√”。
A D
( )拼成一个和梯形面积相等的长方形
( )长方形的宽与梯形的高相等 E F
( )长方形的长是梯形上底与下底之和的一半
( )梯形的面积=(上底+下底)÷2×高 B C
目标序号 090604 核心素养 推理意识(水平二) 认知维度 应用
预估难度 中 预估时长 5 分钟 设计方式 创编
设计意图 考查学生能否在理解梯形面积计算推导的基础上 ,独立 自主探究不一样的推导方法。 通过观察图形, 思考“ 出入相补” 原理,理解面积计算公式的本质,渗透转化思想,并通过学习我国古代数学家的方法, 感受数学文化的魅力。
第四课时 组合图形的面积
★基础素养★
【题 1】学习小组正在研究怎样计算组合图形的面积。
12 m
(
4m
)10 m
15m
(1)你能看懂小维和小思的方法吗?请在图中画一画,并说一说你是怎么想的。
(
我是这样算的:
12×4
+(
12+15
)
×6÷2
12 m
)
(
我是这样算的:
(
12+15
)
×10÷2
-
4×3÷2
12
m
4m
10
m
) (
4m
)10 m
15m
把图形分割成( )形和( )形。
15m
补上一个( )形,把图形转化成一个( )形。
(2)你还有不一样的计算方法吗?请在图中画出辅助线并列式计算。
12 m
(
4m
)10m
15m
(
比较一下大家不同的计算方法,你有
什么新的收获?
)
目标序号 090601 核心素养 空间观念(水平三) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 创编
设计意图 结合图形和算式,引导学生进行分割和说理,从正向思维和逆向思维两 个角度考查学生对组合图形面积计算的掌握情况,进一步理解组合图形的面 积计算的思考过程和具体的计算方法,发展空间观念。
★能力素养★
【题 2】我们日常使用的口罩呈长方形,尺寸如图 1。为便于佩戴时展开,口罩加工时中间要做三条折叠,每条折叠折进的宽度为 1cm(图 2 中B点到C点的长度)。制作 这个口罩,至少需要多少布料?(图 2 中F点和H点重合)
目标序号 090603 核心素养 应用意识(水平二) 认知维度 应用
预估难度 易 预估时长 5 分钟 设计方式 选编
设计意图 运用组合图形出入相补原理 ,将口 罩折叠的面积转化成长方形的面积,再选择合理的方法解决问题,体会解决问题的方 法和策略的多样性,培养分析、解决问题的能力,感受数学与 生活的密切联系。
★综合应用★
【题 3】明代戈汕著的《蝶几图》是中国古代组合家具的设计图。“几”指的是桌型器具,“蝶几”的桌面有 6 种基本形状,共 13 张,可以根据需要自由组合,蝶
几图中共计列出了 8 类 76 种不同图案形状的组合桌。
下图就是一套“蝶几”模型的平面设计图(每格长 1dm)。
《蝶几图》中有一种拼组好的桌面,名为“葵实”,形状如图。这张“葵实” 桌面的面积是 dm2。
“葵实”可以由哪几种基本形状的桌面拼组成,把你的拼组方案画在图中。( 注意每种基本形状桌面的张数。)
目标序号 090604 核心素养 应用意识(水平二) 创新意识(水平二) 认知维度 应用
预估难度 中 预估时长 8 分钟 设计方式 选编
设计意图 通过阅读数学材料,进行数学文化、数学思想的渗透,同 时考查梯形面积公式的灵活运用。认识《 蝶几图》的基本图形及拼组方法,吸取知识的同时发展数学思维。通过渗透数学文 化开阔视野, 增强数学学习的兴趣。
第五课时 不规则图形的面积
★基础素养★
【题 1】小朋友刚出生,就有了第一个身份的证明“足印”。
下面是小思刚出生时的足印,这个足印大约有多大呢?请你把解决问题的思路和结果写出来。(下图中每个小方格的面积是 1cm2)
方法一:
方法二:
比较一下这两种估测的结果,差距大吗?想想有可能是什么原因?
目标序号 090601 核心素养 量感(水平三) 认知维度 理解
预估难度 易 预估时长 5 分钟 设计方式 创编
设计意图 能熟练运用数方格和转化为近似的规则图形的方法估测不规则图形的 面积,体会估算策略和方法的多样性和差异性,进一步发展量感。
★能力素养★
【题 2】小维和同学们在研究一棵树一年大约能吸收多少克二氧化碳。
先捡一片大小中等的落叶,测量它的面积。
以下是 3 位同学测量的过程,他们估测的结果分别是多少?
约( )cm2 约( )cm2 约( )cm2
比较三人的估测结果,你有什么想说的?你认为谁估计的结果更准确些?为什么?
假如每平方米树叶每天能吸收约 5 克二氧化碳,一棵树有 10000 片这样的树叶,
那么这棵树一年(按 365 天计算)大约能吸收多少克二氧化碳?
目标序号 090603 核心素养 量感(水平三) 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 7 分钟 设计方式 改编
设计意图 运用不同方格测量同一物体的面积 ,进行 直观的估测和比较,感悟估测范围与结果随测量单位变小而越来越准确,发展 学生的空间观念和量感, 积累数学活动经验。
★综合应用★
【题 3】在我们熟悉的方格图中,每一组横纵线的交点就叫做一个格点,以格点为顶点画出的多边形叫做“格点多边形”。
“格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能用计算公式来表达吗?”
(
多边形面积
=
内部点数
+
边线点数
÷
2-1
)数学家毕克多年研究格点多边形的面积,终于找到了格点数目与图形面积的关系, 近似证明得出“毕克”定理:顶点都在正方形格点上的多边形,如下图,内部点(绿色) 点数直接计入面积,边线点(紫色和红色)点数除以 2 后,再减 1,所以得到
(1)根据这段话的描述,你能算出图 1 中的多边形的面积吗?
图 1 图 2
用我们学习估算多边形面积的方法在图 2 中验证一下。
你觉得格点多边形面积有趣吗?在右边的方格纸上设计一个多边形,并算算它的面积吧!(内部点用○表示,边线点用●表示)
目标序号 090604 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 8 分钟 设计方式 创编
设计意图 通过阅读相关材料,拓展数学文化,丰富多边形面积的估 测方法,知识获得的同时经历了阅读理解、尝试运用、验证检 查、 内化应用的过程, 培养学生数学阅读能力和应用意识。
单元素养作业
★知识地图★
学习了这个单元,你能整理本单元的学习内容吗?可以用文字、表格或思维导图, 也可以是其他你喜欢的方式,试试看吧!完成之后可以和小伙伴互相交流,进一步完善整理的内容。
目标序号 090605 核心素养 创新意识 认知维度 创新
预估难度 中 预估时长 10 分钟 设计方式 创编
设计意图 激发学生对本单元所学习内容的深层次的思考,通过整理突出核心知识, 建立知识之间的联系,体现知识内在的逻辑关系;通过文字、表格或思维导图 使核心内容可视化、结构化,进一步把握知识脉络,形成整体、全面的认识。
★基础素养★
(
2cm
6cm
8cm
)【题 1】小维的学校要建一面艺术墙(如图所示),要给这面墙
刷一层底漆,要刷的面积有多大? (1)用分割的方法算一算:
(
我把图形分割成
2cm
6cm
8cm
)
①
(
我把图形分割成
2cm
6cm
8cm
)
②
下面这 4 种方法可以计算墙面的面积吗?试着说一说理由。
(
可以动手剪一剪,拼一拼。
)
③ ④ ⑤ ⑥
( ) ( ) ( ) ( )
你能看懂他们的方法吗?试着画图并简要说明。
(
2cm
6cm
8cm
) (
2cm
6cm
8cm
)小芳是这样算的:8×8-(8÷2)×2÷2×2 小明是这样算的:(6+8)×8÷2
⑦ ⑧
如果要给这些方法分分类,可以怎样分类?试着分一分、写一写。
目标序号 090605 核心素养 几何直观(水平三) 认知维度 分析
预估难度 中 预估时长 8 分钟 设计方式 创编
设计意图 运用等积变换的思想,用分割法、割补法、添补法、等积变形法把组合 图形转化成已学过的图形来计算面积,培养学生空间想象能力,通过分类, 进一步沟通不同的转化方法之间的联系,数形结合,建立不同方法的模型。
★能力素养★
【题 2】(1) 星期六,小思和小维在研究数学问题。
A点往左平移( )格变成( ) 形,如果用梯形面积公式计算它的面积:
A点往右平移到与B点重合变成( ) 形,如果用梯形面积公式计算它的面积:
通过计算,你有什么发现?
(2)星期天,小维与爸爸来到木材厂,看到一堆木头,如图。聪明的小维运用数学知识,列出了算式:
(3+6)×4÷2
他很快算出了木头的数量,他的这种计算方法其实是( + )×层数÷2。这是什么道理呢?
(3)爸爸给小维提了一个问题:“你能用刚才的方法来计算下面算式的和吗?” 1+2+3+4+5+……+98+99+100=
你能帮助小维解决这个问题吗?请写出思考过程。
目标序号 090605 核心素养 几何直观(水平三) 模型意识(水平三) 认知维度 分析
预估难度 中 预估时长 10 分钟 设计方式 创编
设计意图 沟通各平面图形面积计算之间的联系 ,理解 梯形面积公式作为“ 通用公式”的含义,以及它在实际生活中的应用,将图形的面积计算、等差数列等内容综合考查,数形结合,提高学 生的模型意识。
★综合应用★
【题 3】《九章算术》方田章主要论述平面图形直线形和圆的面积计算方法。其中第一题“今有田广十五步,从(音纵 zong)十六步。问为田几何。”“答曰:一亩”。这里“广”就是宽,“从”即纵,指其长度,“方田术”曰:广从步数相乘得积步(得积
步就是得到乘积的平方步数)。意思就是一块长方形的田地,宽边是十五步,长边是十六步,这块田的面积就是一亩。
请在图中画出面积约为一亩的图形。(如图 1 方格图所示:正方形小格的边长表示一步长)
(图 1)
王大爷要把一块梯形的田,平均分给三个儿子,每个儿子分得几亩田?(如图2 所示:正方形小格的边长表示一步长)
(图 2)
请帮王大爷在图 2 中将田平均分一分,分成面积相等的三份。
目标序号 090605 核心素养 应用意识(水平二) 认知维度 应用
预估难度 中 预估时长 8 分钟 设计方式 创编
设计意图 通过了解古人测量和计量土地面积的方法, 考查长方形、梯形面积公式的灵活运用,利用数方格、计算公式等多边形面积计算的方法,增强学生学习的兴趣、开阔视野,提高文化素养和应用能力。
评价工具答案解析
【题 1】
第一课时 《平行四边形的面积》答案解析
(1)A: 6×5=30(cm2) B: 12×10=120(cm2) C:24×20=480(cm2)
(2)(答案不唯一)如:
图形 A B C
底 6cm 12cm 24cm
高 5cm 10cm 20cm
面积 30cm2 120cm2 480cm2
发现:平行四边形的底和高同时扩大为原来的 2 倍,面积扩大到原来的 4 倍。
【题 2】
(1)小维的观点不对,因为书本摆成的长方形变成平行四边形后边长变了,周长也变大了,但是高不变,所以面积也不变。
(2)( B)
A:6×118.6=111.6 用了平行四边形的两条邻边相乘,所以是错误的。B:5×15.5=77.5,用了平行四边形的两条高相乘,所以是错的。 C:5×6=30,用了平行四边形的一条边和不对应的一条高相乘,所以是错的。
启示:计算平行四边形的面积要采用底和高对应的数据。
【题 3】
探究性学习指导意见:
鼓励学生独立自主探究,遇到困难可寻求同学、老师或家长的帮助和指导。
鼓励学生以小组为学习单位合作学习,相互交流、合作探究。
在探究活动中,可以对有困难的学生提供帮扶,对学有余力的学生给予指导,确保学生在课后规定的时间内完成。
采用多样化得评价方式,关注学生探究态度、探究能力和合作学习能力得提升。
第二课时 《三角形的面积》答案解析
【题 1】
(
△ ABC
△
ABC1
)(1)① S =10×12÷2=60 (cm2) ② S =10×12÷2=60 (cm2)
(
△ ABC2
△
ABC3
)③ S = 10×12÷2=60 (cm2) ④ S =10×12÷2=60 (cm2)
(2)(答案不唯一)我发现了:这四个三角形的面积相等,因为他们都等底等高,所以面积相等。
(3) A
【题 2】
(1)1.4×2.5÷2×750=1312.5(吨)
(2)( ③ ) 画图(答案不唯一)
【题 3】
(1)100×33÷2=1650(cm2)
(2)假设 10m2 的布是长 10m,宽是 1m 的长方形。(可以画示意图) 10m=1000cm 1m=100cm
1000÷100=10(个) 100÷33=3(组)
10+(10-1)=19(个) 19×3=57(条)
【题 4】
180÷30×2=12(cm)或者 180×2÷30=12(cm)
第三课时 《梯形的面积》答案解析
【题 1】(方法不唯一)
[10+(6×2+10)]×8÷2=128(cm2)
反思:梯形的下底=三角形的底×2+上底,再根据梯形面积公式计算面积,答案正确。
【题 2】前窗玻璃面积大(方法不唯一) 方法一:
(40+71)×40÷2=2220(cm2) (45+65)×40÷2=2200(cm2) 2220>2200
方法二:
两个梯形的高相等,只要比较它们的两底之和 。
40+71=111(m) 45+65=110(m) 111>110
方法三:
比较梯形的各部分组成元素,即分别比较两个梯形的高、上底、下底,得到差值, 也可以比较出面积的大小。
【题 3】
(1)(65-25)×25÷2=500(m2)
(2)方法一:(500+75)÷25=23(m) 方法二: 75×2÷25=6(m)
(65-25+6)÷2=23(m)
【题 4】
( √ )拼成一个面积相等的长方形
( √ )长方形的宽与梯形的高相等
( √ )长方形的长是梯形上底与下底之和的一半
( √ )梯形的面积=(上底+下底)÷2×高
第四课时 《组合图形的面积》答案解析
【题 1】
(1) 长方 梯 三角 梯
(2)(答案不唯一)
预设:12×4+15×6÷2 12×3+3×6÷2 15×10-(4+10)×3÷2
收获:计算组合图形的面积时,可以用分割法或割补法进行计算。
【题 2】
分析:
这个口罩展开后的面积也就是长为 18 厘米,宽为(4+1×2×3+1×2+3)厘米的长方形的面积,长方形的面积=长×宽,代入即可。
方法一:18×(4+1×2×3+1×2+3)=270(cm2)
方法二:18×1×8=144(cm2) 18×4=72(cm2) 18×3=54(cm2) 144+72+54=270(cm2)
【题 3】
分析:通过观察图形可知,把拼组好的桌面分成两个完全一样的图形,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。(2+6)×2÷2×2=16(平方分米)
分析:根据“几”的基本图形可知,这个“葵实”可以由“左半斜”一张,“右半斜”一张,“ 小三斜”一张拼组成。作图如下:
或由“左半斜”一张(“右半斜”一张),“小三斜”一张,“闰”一张拼组成的。作图如
下:
第五课时 《不规则图形的面积》答案解析
【题 1】
方法一:我用数方格的方法,满格的有 5 格,就是 5cm2,不满格的有 16 格,都按半格算,所以足印的面积:5+16÷2=13(cm2)
方法二:我把足印转化成近似的梯形,如图,梯形的上底是 4 厘米,下底是 2 厘米,高是 5 厘米,所以足印的面积大约是:(4+2)×5÷2=15(cm2)
这两种估测的结果差距不大。估测都会有一些差距,因为估测时选择的方法不一样, 得到的数据就会不一样,结果也就不一样。但在估测时,不管用数方格的方法,还是转化成近似的规则图形,都应该尽量做到接近准确,所以差距不大。(分析原因的答案不唯一,合理即可。)
【题 2】
(1) 约(36)cm2 约(34)cm2 约(29)cm2
(2)三人所用的测量方格纸的规则不一样,第一人用的一格是 9cm2 的方格纸,第二人用的是 4cm2 的方格纸,第三人用的是 1cm2 的方格纸,所以他们侧量的结果也不一样,随着方格的大小逐渐变小,估测出来的结果也逐渐变小。
我认为第三人的估测结果更准确。因为,它的格子的边长最小,所以测量得的结果最接近准确值。
(3) 29cm2=0.29dm2=0.0029m2 0.0029×10000×5×365
=29×5×365
=145×365
=52925(克)
【题 3】
(1)39+14÷2-1=45(cm2)
(2) 如下图,我把多边形转化成一个近似的梯形,梯形的上底是 8 厘米,下底是 7 厘
米,高是 6 厘米,所以这个多边形的面积大约是:(8+7)×6÷2=45(cm2)
(答案不唯一,结果在 45cm2 左右,算式或过程合理均对)
(3)答案略,答案不唯一。
单元素养作业
【题 1】
分割法:① 分割成 1 个三角形和一个长方形
8×2÷2+8×6=56(cm2)
② 分割成 2 个完全相同的梯形(6+8)×(8÷2)÷2×2=56(cm2)
(2)( √ ) ( √ ) ( √ ) (√ ) 割补法: ③ 转化成一个大长方形和小长方形
8×6+(8÷2)×2=56(cm2)
④ 转化成一个长方形
(8+6)× (8÷2)=56(cm2)
⑤ 转化成一个平行四边形
(8+6)× (8÷2)=56(cm2)
⑥ 转化成一个梯形
(6+6+8+8)×(8÷2)÷2=56(cm2)
(3)小芳:
添补法:⑦ 添补成一个正方形,再减去多算的 2 个三角形的面积
8×8-(8÷2)×2÷2×2=56(cm2)
小明:
等积变形法:⑧ 根据“2 个等底等高的三角形面积相等”,转化成一个梯形
(6+8)×8÷2=56(cm2)
(4) 分割法:①②②
割补法:③④⑤⑥ 添补法:⑦
等积变形法:⑧
【题 2】
(1)3,平行四边,(5+5)×2÷2=10,三角,(0+5)×2÷2=5
发现:运用梯形的面积计算公式也可以算出其他图形的面积,可以说它是一个“万能公式”。
上层根数,下层根数。学生能够用梯形面积计算公式去说明理由,合理即可。
学生可以通过画图、计算进行说理。
【题 3】
(1)16×15=240(平方步)
240 平方步=1 亩 (图略)
(2)(24+48)×20÷2÷240÷3=1(亩)
(3)因为梯形的下底是上底的 2 倍,所以把这个梯形分成等底等高的 3 个三角形即可。
