2021-2022学年黑龙江省鸡西市密山市六年级(上)期末数学试卷(五四学制)(pdf版含解析)
文档属性
| 名称 | 2021-2022学年黑龙江省鸡西市密山市六年级(上)期末数学试卷(五四学制)(pdf版含解析) |  | |
| 格式 | |||
| 文件大小 | 457.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 15:21:36 | ||
图片预览



文档简介
2021-2022 学年黑龙江省鸡西市密山市六年级(上)期末数学试
卷(五四学制)
一、选择题(每小题 3 分,满分 30 分)
1.(3分) 用分数乘法表示哪个正确( )
A.4× B.5× C.5 D.5﹣
2.(3分)下列算式中,( )的计算结果最大.
A. B.1× C. D.
3.(3分)哪种统计图可以表示各部分数量与总数之间的关系.( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.直方图
4.(3分)( )×24= ×24+ ×24.这是运用了( )
A.乘法交换律 B.乘法结合律
C.乘法分配律 D.加法结合律
5.(3分)在推导圆的面积公式时,把一个圆分成若干等份后,拼成一个近似长方形( )
A.圆的半径 B.圆的直径
C.圆的周长 D.圆周长的一半
6.(3分)两根同样长的铁丝,一根用去了 ,另一根用去了 米,( )
A.第一根长 B.第二根长
C.一样长 D.无法比较哪根长
7.(3分)一辆汽车每小时行驶 80千米, 小时行驶的路程( )80千米.
A.大于 B.小于 C.等于 D.无法比较
8.(3分)把 30%的百分号去掉,原来的数就( )
A.扩大 100倍 B.缩小 100倍 C.不变 D.无法判断
9.(3分)一件商品先提价 ,再降价 ,现价与原价相比( )
A.涨了 B.降了
C.与原价相等 D.无法确定
10.(3分)3吨的 和 5吨的 相比( )
A.3吨的 重 B.5吨的 重 C.一样重 D.不确定
二、填空题(每小题 3 分,满分 30 分)
11.(3 分) : = =80%= ÷5= (填小
数).①: .
12.(3分)把 : 化成最简整数比是 : ,比值是 .
13.(3分) 小时= 分.
14.(3分)一袋米,甲一人可吃 24天,乙一人可吃 36天,这袋米可吃 天.
15.(3分) 的倒数是 ,2 倒数是 .
16.(3 分)边长是 10米的正方形中放置一个最大的圆,这个圆的面积是 平方
米.
17.(3 分)一个圆的半径扩大到原来的 2 倍,则周长扩大到原来的 倍,面积扩大
到原来的 倍.
18.(3分)把 5米长的铁丝平均分成 6段,每段占全长的 .
19.(3 分)六年级某班今天出勤 47 人,有 3 人因病请假,今天这个班学生的出勤率
是 .
20.(3分)用火柴棒按图的方式摆图形,第 30个图形需要 根火柴棒.
三、计算题(共计 12 分)
21.(12分)(1) ;
(2) ×24;
(3)2.1×( ﹣ );
(4) × ;
(5) + ;
(6) ×34×7× .
四、操作题(共计 4 分)
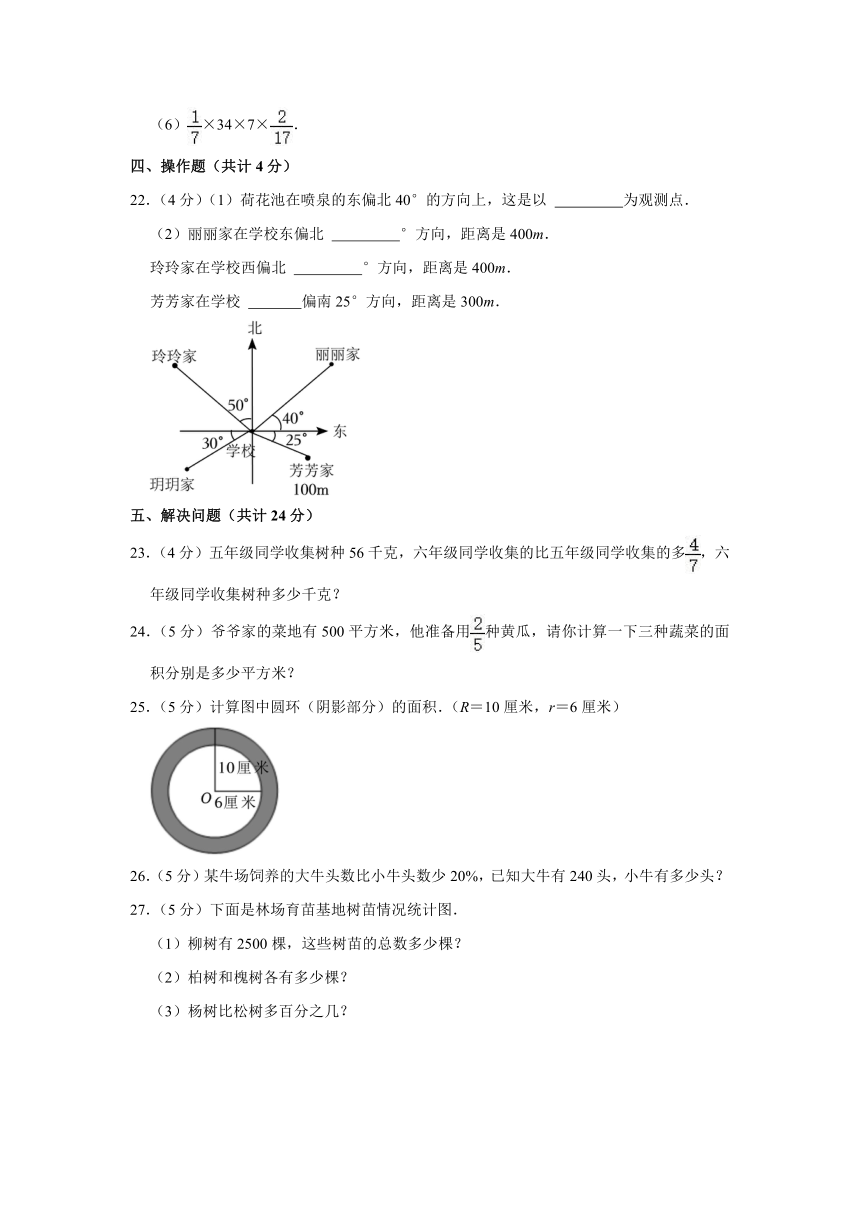
22.(4分)(1)荷花池在喷泉的东偏北 40°的方向上,这是以 为观测点.
(2)丽丽家在学校东偏北 °方向,距离是 400m.
玲玲家在学校西偏北 °方向,距离是 400m.
芳芳家在学校 偏南 25°方向,距离是 300m.
五、解决问题(共计 24 分)
23.(4分)五年级同学收集树种 56千克,六年级同学收集的比五年级同学收集的多 ,六
年级同学收集树种多少千克?
24.(5分)爷爷家的菜地有 500平方米,他准备用 种黄瓜,请你计算一下三种蔬菜的面
积分别是多少平方米?
25.(5分)计算图中圆环(阴影部分)的面积.(R=10厘米,r=6厘米)
26.(5分)某牛场饲养的大牛头数比小牛头数少 20%,已知大牛有 240头,小牛有多少头?
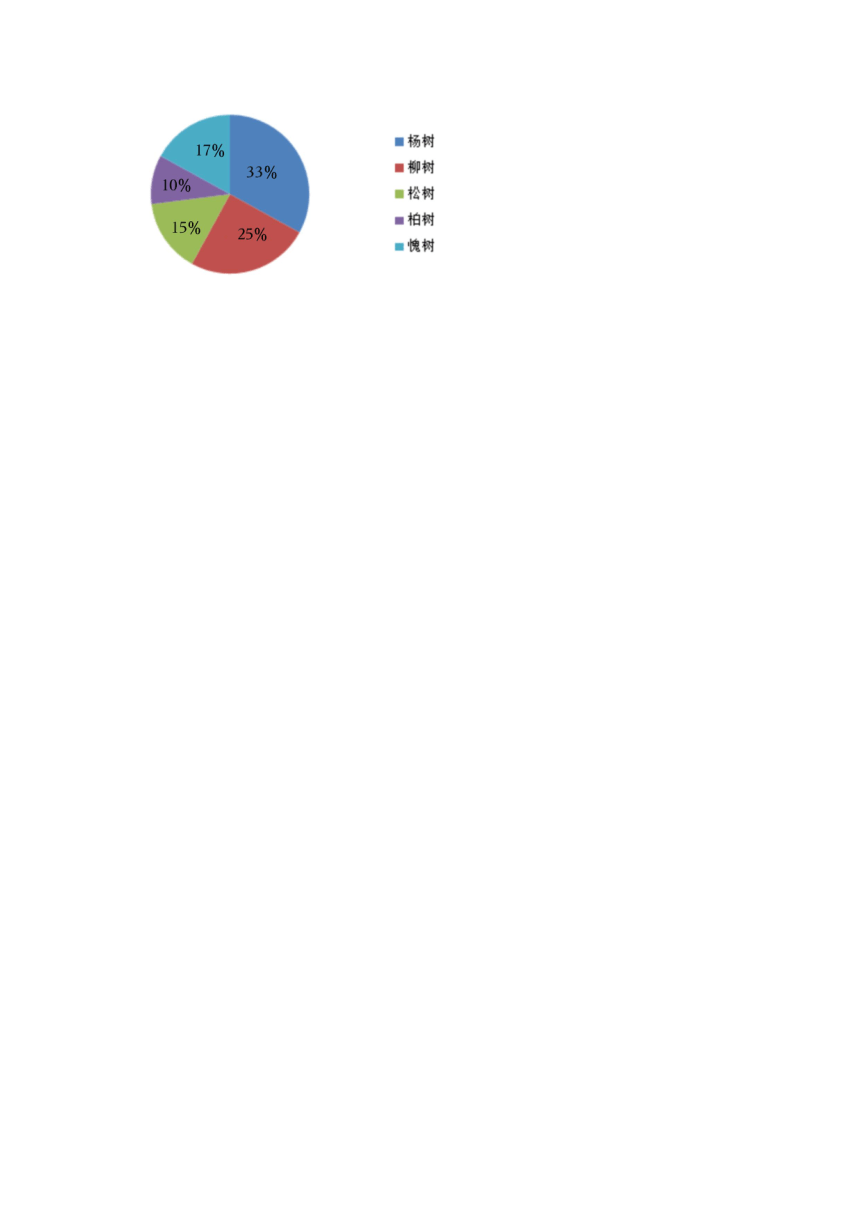
27.(5分)下面是林场育苗基地树苗情况统计图.
(1)柳树有 2500棵,这些树苗的总数多少棵?
(2)柏树和槐树各有多少棵?
(3)杨树比松树多百分之几?
2021-2022 学年黑龙江省鸡西市密山市六年级(上)期末数学试
卷(五四学制)
参考答案与试题解析
一、选择题(每小题 3 分,满分 30 分)
1.【分析】根据分数乘法的意义解答即可.
【解答】解: 用分数乘法表示 .
故选:B.
【点评】本题考查了分数的混合运算,掌握分数乘法的意义是解答本题的关键.
2.【分析】根据分数乘法法则计算,分子相乘的积作分子,分母相乘的积作分母,能约分的
要先约分再计算比较简便.
【解答】解: × = ,1× = , × = , × = ,
以上计算结果中, 最大.
故选:C.
【点评】此题考查了有理数的乘法,牢固掌握分数乘法法则是解题的关键.
3.【分析】根据扇形统计图特征解答即可.
【解答】解:能清楚地表示出各部分数量与总数之间的关系的是扇形统计图.
故选:B.
【点评】此题考查的是扇形统计图,应根据条形统计图、折线统计图、扇形统计图各自
的特点进行解答.
4.【分析】根据乘法分配律求解即可.
【解答】解:( )×24= ×24,
故选:C.
【点评】本题主要考查有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和
运算法则与运算律.
5.【分析】把圆等分成若干份,可以发现把圆等分的份数越多,拼成的图形就越接近一个长
方形,这个长方形的面积也就越接近于圆的面积,故就由长方形的面积公式推导出圆的
面积公式.
【解答】解:如图所示,
图中近似长方形的一边 a的长度相当于圆的半径;另一边 b的长度相当于圆的周长的一
半.
故选:D.
【点评】本题考查了圆与近似长方形的关系以及圆的周长,解答此题的关键是把图形的
变化识别出来.
6.【分析】D可以分三种情况考虑:(1)总长小于 1米时;(2)总长等于 1米时;(3)大于
1米时.
【解答】解:分三种情况:
(1)总长小于 1米时,假设全长为 米,
则第一根剩: (米) (米), ;
(2)总长等于 1米时,
第一根剩的长度为: (米) (米);
(3)总长大于 1米时,假设为 3米时,
第一根剩的长度为: (米) (米), .
所以无法比较.
故选:D.
【点评】本题考查了分数的实际应用,解决实际问题时要分情况考虑,最后综合下结论.
7.【分析】设 小时行驶的路程为 x千米,则根据“每小时行驶 80千米”和“路程、时间、
速度的数量关系”列出方程并解答,然后将 x的值与 80比较大小即可.
【解答】解:设 小时行驶的路程为 x千米
= .
解得 x=72.
因为 72<80,
所以 小时行驶的路程小于 80千米.
故选:B.
【点评】本题主要考查了一元一次方程的应用,解题的关键是读懂题意,找到关键描述
语,列出等量关系.
8.【分析】由百分数的概念,即可得到答案.
【解答】解:把 30%的百分号去掉,原数变成 30,
∴原来的数扩大 100倍.
故选:A.
【点评】本题考查百分数,关键是掌握百分数的概念.
9.【分析】设商品原价为 a,商品先提价 后售价为(1+0.1)a,再降价 后的售价为(1+0.1)
(1﹣0.1)a.
【解答】解:设商品原价为 a,
现在售价为(1+0.3)(1﹣0.7)a=0.99a,
∵a>0.99a,
∴现价与原价相比降了.
故选:B.
【点评】此题考查了一元一次方程的应用,弄清题意,找到等量关系是解本题的关键.
10.【分析】算出 3吨的 和 5吨的 ,即可得到答案.
【解答】解:∵3× = (吨) = (吨),
∴3吨的 和 5吨的 ,
故选:C.
【点评】本题考查分数乘法的应用,解题的关键是掌握分数乘法的法则.
二、填空题(每小题 3 分,满分 30 分)
11.【分析】根据分数、小数、百分数的关系计算即可.
【解答】解:4:5= =80%=4÷5=0.3.
故答案为:4,5,3,0.8.
【点评】本题考查了分数、小数、百分数的关系,正确计算是关键.
12.【分析】根据整数比,比值的定义求解即可.
【解答】解: : =5:7=1.25.
故答案为:5:4,1.25.
【点评】本题考查最简整数比,比值等知识,解题的关键是掌握整数比的化简方法,属
于中考常考题型.
13.【分析】用 小时乘以 60,即可得出答案.
【解答】解: ×60=36(分).
故答案为:36.
【点评】此题考查了数学常识,掌握把高级单位的名数换算成低级单位的名数,就乘单
位间的进率是解题的关键.
14.【分析】把一袋米看成单位“1”,再根据题意列式进行计算即可.
【解答】解:由题可知,1÷( )
=1÷( + )
=2÷( + )
=6÷
=4(天).
故答案为:8.
【点评】本题考查分数混合运算的应用,能够根据题意列出式子是解题的关键.
15.【分析】根据乘积是 1的两数互为倒数解答即可.
【解答】解: 的倒数是 4;2 .
故答案为:3, .
【点评】本题考查了倒数,掌握倒数的定义是解答本题的关键.
16.【分析】在一张边长 10米的正方形纸片上剪下一个圆,当圆的直径等于 10米时,剪下
的圆最大,由直径可求圆的面积.
【解答】解:当剪下圆的直径等于正方形的边长时,圆的面积最大,
此时,圆的直径为 10米,
所以圆的面积为π×52=25π(平方米).
故答案为:25π.
【点评】本题考查了正方形和圆的认识,掌握当剪下圆的直径等于正方形的边长时,圆
的面积最大是关键.
17.【分析】圆的半径扩大到原来的 2倍,周长扩大到原来的 2倍,面积也扩大到原来的 4
倍.
【解答】解:设圆的半径为 r,则周长为 2πr2,
半径扩大到原来的 7倍,为 2r,
则周长为 4πr,面积为π×(7r)2=4πr7,
∴圆的半径扩大到原来的 2倍,周长扩大到原来的 2倍.
故答案为:6,4.
【点评】本题考查了圆的周长与面积,解题的关键是掌握圆的周长与面积公式.
18.【分析】把绳子的全长看作单位“1”,平均分成 6段,每段是全长的 .
【解答】解:把 5米长的绳子平均分成 6段,每段是全长的 .
故答案为: .
【点评】本题主要考查了分数的意义,关键是掌握分数的意义.
19.【分析】用出勤人数除以总人数即可得到出勤率.
【解答】解:47÷(47+3)
=47÷50
=0.94
=94%.
故答案为:94%.
【点评】本题考查了百分数的应用,理解出勤率的意义是解题的关键.
20.【分析】不难看出,第 n个图形需要的火柴棒为 4n,从而可求解.
【解答】解:由图可知:
第 1个图形需要的火柴棒根数为 4;
第 5个图形需要的火柴棒根数为 8=4×7;
第 3个图形需要的火柴棒根数为 12=4×6;
…,
则搭第 n个图形需要火柴根数为:4n,
∴第 30个图形需要的火柴棒根数为:4×30=120(根).
故答案为:120.
【点评】本题主要考查图形的变化规律,解题的关键在于通过题中图形的变化情况,通
过归纳与总结找出普遍规律求解即可.
三、计算题(共计 12 分)
21.【分析】(1)根据有理数的乘法法则计算即可;
(2)根据有理数的乘法法则计算即可;
(3)根据乘法分配律计算即可;
(4)从左到右计算即可;
(5)根据乘法分配律计算即可;
(6)根据乘法交换律和结合律计算即可.
【解答】解:(1) = ;
(2) ×24=20;
(3)2.2×( ﹣ )
=2.7× ﹣5.1×
=1.4﹣6.9
=0.8;
(4) ×
=
= ;
(5) +
= ×( )
= ×1
= ;
(6) ×34×4×
=( ×7)×(34× )
=7×4
=4.
【点评】本题考查有理数的混合运算,熟练掌握运算法则和运算顺序是解答本题的关键,
注意乘法分配律的应用.
四、操作题(共计 4 分)
22.【分析】方向角是从正北或正南方向到目标方向所形成的小于 90°的角,由此即可解答.
【解答】解:(1)荷花池在喷泉的东偏北 40°的方向上,这是以喷泉为观测点,
故答案为:喷泉;
(2)丽丽家在学校东偏北 40°方向,距离是 400m;
玲玲家在学校西偏北 40°方向,距离是 400m;
芳芳家在学校东偏南 25°方向,距离是 300m.
故答案为:40,40,东.
【点评】本题考查方向角的概念,掌握方向角的定义是解题的关键.
五、解决问题(共计 24 分)
23.【分析】根据分数乘法的意义解答即可.
【解答】解:56×(1+ )
=56×
=88(千克).
答:六年级同学收集树种 88千克.
【点评】本题考查了分数混合运算的应用,掌握分数乘法的意义是解答本题的关键.
24.【分析】先求出种黄瓜的面积,从而可求出剩下的面积,再利用所给的条件即可求解.
【解答】解:种植黄瓜的面积为:500× =200(平方米),
则剩下的面积为:500﹣200=300(平方米),
则种植西红柿的面积为:300× =240(平方米),
种植辣椒的面积为:300× =60(平方米).
答:种植黄瓜的面积为 200平方米,种植西红柿的面积为 240平方米.
【点评】本题主要考查比的应用,分数的混合运算,解答的关键是对相应的运算法则的
掌握.
25.【分析】分别求出两圆的面积,再相减即可.
【解答】解:∵两圆的半径分别为 10厘米,6厘米,
∴图中圆环(阴影部分)的面积是(102﹣72)π=64π(平方厘米),
答:图中圆环(阴影部分)的面积是 64π平方厘米.
【点评】此题主要考查了认识平面图形,正确记忆圆环的面积公式是解题关键.
26.【分析】根据题意可得到小牛的头数是大牛的头数的 80%,从而可求解.
【解答】解:小牛的头数为:
240×(1﹣20%)
=240×80%
=192(头).
答:小牛有 192头.
【点评】本题主要考查百分数的应用,解答的关键是理解清楚题意找到等量关系.
27.【分析】(1)用柳树棵数 2500除以 25%即可;
(2)用总棵数分别乘以柏树和槐树的百分比即可;
(3)用杨树的百分比减去松树的百分比即可.
【解答】解:(1)2500÷25%=10000(棵),
答:这些树苗的总数 10000棵;
(2)10000×10%=1000(棵),
10000×17%=1700(棵),
答:柏树和槐树各有 1000棵和 1700棵;
(3)(33%﹣15%)÷15%=120%,
答:杨树比松树多 120%.
【点评】本题考查扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
卷(五四学制)
一、选择题(每小题 3 分,满分 30 分)
1.(3分) 用分数乘法表示哪个正确( )
A.4× B.5× C.5 D.5﹣
2.(3分)下列算式中,( )的计算结果最大.
A. B.1× C. D.
3.(3分)哪种统计图可以表示各部分数量与总数之间的关系.( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.直方图
4.(3分)( )×24= ×24+ ×24.这是运用了( )
A.乘法交换律 B.乘法结合律
C.乘法分配律 D.加法结合律
5.(3分)在推导圆的面积公式时,把一个圆分成若干等份后,拼成一个近似长方形( )
A.圆的半径 B.圆的直径
C.圆的周长 D.圆周长的一半
6.(3分)两根同样长的铁丝,一根用去了 ,另一根用去了 米,( )
A.第一根长 B.第二根长
C.一样长 D.无法比较哪根长
7.(3分)一辆汽车每小时行驶 80千米, 小时行驶的路程( )80千米.
A.大于 B.小于 C.等于 D.无法比较
8.(3分)把 30%的百分号去掉,原来的数就( )
A.扩大 100倍 B.缩小 100倍 C.不变 D.无法判断
9.(3分)一件商品先提价 ,再降价 ,现价与原价相比( )
A.涨了 B.降了
C.与原价相等 D.无法确定
10.(3分)3吨的 和 5吨的 相比( )
A.3吨的 重 B.5吨的 重 C.一样重 D.不确定
二、填空题(每小题 3 分,满分 30 分)
11.(3 分) : = =80%= ÷5= (填小
数).①: .
12.(3分)把 : 化成最简整数比是 : ,比值是 .
13.(3分) 小时= 分.
14.(3分)一袋米,甲一人可吃 24天,乙一人可吃 36天,这袋米可吃 天.
15.(3分) 的倒数是 ,2 倒数是 .
16.(3 分)边长是 10米的正方形中放置一个最大的圆,这个圆的面积是 平方
米.
17.(3 分)一个圆的半径扩大到原来的 2 倍,则周长扩大到原来的 倍,面积扩大
到原来的 倍.
18.(3分)把 5米长的铁丝平均分成 6段,每段占全长的 .
19.(3 分)六年级某班今天出勤 47 人,有 3 人因病请假,今天这个班学生的出勤率
是 .
20.(3分)用火柴棒按图的方式摆图形,第 30个图形需要 根火柴棒.
三、计算题(共计 12 分)
21.(12分)(1) ;
(2) ×24;
(3)2.1×( ﹣ );
(4) × ;
(5) + ;
(6) ×34×7× .
四、操作题(共计 4 分)
22.(4分)(1)荷花池在喷泉的东偏北 40°的方向上,这是以 为观测点.
(2)丽丽家在学校东偏北 °方向,距离是 400m.
玲玲家在学校西偏北 °方向,距离是 400m.
芳芳家在学校 偏南 25°方向,距离是 300m.
五、解决问题(共计 24 分)
23.(4分)五年级同学收集树种 56千克,六年级同学收集的比五年级同学收集的多 ,六
年级同学收集树种多少千克?
24.(5分)爷爷家的菜地有 500平方米,他准备用 种黄瓜,请你计算一下三种蔬菜的面
积分别是多少平方米?
25.(5分)计算图中圆环(阴影部分)的面积.(R=10厘米,r=6厘米)
26.(5分)某牛场饲养的大牛头数比小牛头数少 20%,已知大牛有 240头,小牛有多少头?
27.(5分)下面是林场育苗基地树苗情况统计图.
(1)柳树有 2500棵,这些树苗的总数多少棵?
(2)柏树和槐树各有多少棵?
(3)杨树比松树多百分之几?
2021-2022 学年黑龙江省鸡西市密山市六年级(上)期末数学试
卷(五四学制)
参考答案与试题解析
一、选择题(每小题 3 分,满分 30 分)
1.【分析】根据分数乘法的意义解答即可.
【解答】解: 用分数乘法表示 .
故选:B.
【点评】本题考查了分数的混合运算,掌握分数乘法的意义是解答本题的关键.
2.【分析】根据分数乘法法则计算,分子相乘的积作分子,分母相乘的积作分母,能约分的
要先约分再计算比较简便.
【解答】解: × = ,1× = , × = , × = ,
以上计算结果中, 最大.
故选:C.
【点评】此题考查了有理数的乘法,牢固掌握分数乘法法则是解题的关键.
3.【分析】根据扇形统计图特征解答即可.
【解答】解:能清楚地表示出各部分数量与总数之间的关系的是扇形统计图.
故选:B.
【点评】此题考查的是扇形统计图,应根据条形统计图、折线统计图、扇形统计图各自
的特点进行解答.
4.【分析】根据乘法分配律求解即可.
【解答】解:( )×24= ×24,
故选:C.
【点评】本题主要考查有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和
运算法则与运算律.
5.【分析】把圆等分成若干份,可以发现把圆等分的份数越多,拼成的图形就越接近一个长
方形,这个长方形的面积也就越接近于圆的面积,故就由长方形的面积公式推导出圆的
面积公式.
【解答】解:如图所示,
图中近似长方形的一边 a的长度相当于圆的半径;另一边 b的长度相当于圆的周长的一
半.
故选:D.
【点评】本题考查了圆与近似长方形的关系以及圆的周长,解答此题的关键是把图形的
变化识别出来.
6.【分析】D可以分三种情况考虑:(1)总长小于 1米时;(2)总长等于 1米时;(3)大于
1米时.
【解答】解:分三种情况:
(1)总长小于 1米时,假设全长为 米,
则第一根剩: (米) (米), ;
(2)总长等于 1米时,
第一根剩的长度为: (米) (米);
(3)总长大于 1米时,假设为 3米时,
第一根剩的长度为: (米) (米), .
所以无法比较.
故选:D.
【点评】本题考查了分数的实际应用,解决实际问题时要分情况考虑,最后综合下结论.
7.【分析】设 小时行驶的路程为 x千米,则根据“每小时行驶 80千米”和“路程、时间、
速度的数量关系”列出方程并解答,然后将 x的值与 80比较大小即可.
【解答】解:设 小时行驶的路程为 x千米
= .
解得 x=72.
因为 72<80,
所以 小时行驶的路程小于 80千米.
故选:B.
【点评】本题主要考查了一元一次方程的应用,解题的关键是读懂题意,找到关键描述
语,列出等量关系.
8.【分析】由百分数的概念,即可得到答案.
【解答】解:把 30%的百分号去掉,原数变成 30,
∴原来的数扩大 100倍.
故选:A.
【点评】本题考查百分数,关键是掌握百分数的概念.
9.【分析】设商品原价为 a,商品先提价 后售价为(1+0.1)a,再降价 后的售价为(1+0.1)
(1﹣0.1)a.
【解答】解:设商品原价为 a,
现在售价为(1+0.3)(1﹣0.7)a=0.99a,
∵a>0.99a,
∴现价与原价相比降了.
故选:B.
【点评】此题考查了一元一次方程的应用,弄清题意,找到等量关系是解本题的关键.
10.【分析】算出 3吨的 和 5吨的 ,即可得到答案.
【解答】解:∵3× = (吨) = (吨),
∴3吨的 和 5吨的 ,
故选:C.
【点评】本题考查分数乘法的应用,解题的关键是掌握分数乘法的法则.
二、填空题(每小题 3 分,满分 30 分)
11.【分析】根据分数、小数、百分数的关系计算即可.
【解答】解:4:5= =80%=4÷5=0.3.
故答案为:4,5,3,0.8.
【点评】本题考查了分数、小数、百分数的关系,正确计算是关键.
12.【分析】根据整数比,比值的定义求解即可.
【解答】解: : =5:7=1.25.
故答案为:5:4,1.25.
【点评】本题考查最简整数比,比值等知识,解题的关键是掌握整数比的化简方法,属
于中考常考题型.
13.【分析】用 小时乘以 60,即可得出答案.
【解答】解: ×60=36(分).
故答案为:36.
【点评】此题考查了数学常识,掌握把高级单位的名数换算成低级单位的名数,就乘单
位间的进率是解题的关键.
14.【分析】把一袋米看成单位“1”,再根据题意列式进行计算即可.
【解答】解:由题可知,1÷( )
=1÷( + )
=2÷( + )
=6÷
=4(天).
故答案为:8.
【点评】本题考查分数混合运算的应用,能够根据题意列出式子是解题的关键.
15.【分析】根据乘积是 1的两数互为倒数解答即可.
【解答】解: 的倒数是 4;2 .
故答案为:3, .
【点评】本题考查了倒数,掌握倒数的定义是解答本题的关键.
16.【分析】在一张边长 10米的正方形纸片上剪下一个圆,当圆的直径等于 10米时,剪下
的圆最大,由直径可求圆的面积.
【解答】解:当剪下圆的直径等于正方形的边长时,圆的面积最大,
此时,圆的直径为 10米,
所以圆的面积为π×52=25π(平方米).
故答案为:25π.
【点评】本题考查了正方形和圆的认识,掌握当剪下圆的直径等于正方形的边长时,圆
的面积最大是关键.
17.【分析】圆的半径扩大到原来的 2倍,周长扩大到原来的 2倍,面积也扩大到原来的 4
倍.
【解答】解:设圆的半径为 r,则周长为 2πr2,
半径扩大到原来的 7倍,为 2r,
则周长为 4πr,面积为π×(7r)2=4πr7,
∴圆的半径扩大到原来的 2倍,周长扩大到原来的 2倍.
故答案为:6,4.
【点评】本题考查了圆的周长与面积,解题的关键是掌握圆的周长与面积公式.
18.【分析】把绳子的全长看作单位“1”,平均分成 6段,每段是全长的 .
【解答】解:把 5米长的绳子平均分成 6段,每段是全长的 .
故答案为: .
【点评】本题主要考查了分数的意义,关键是掌握分数的意义.
19.【分析】用出勤人数除以总人数即可得到出勤率.
【解答】解:47÷(47+3)
=47÷50
=0.94
=94%.
故答案为:94%.
【点评】本题考查了百分数的应用,理解出勤率的意义是解题的关键.
20.【分析】不难看出,第 n个图形需要的火柴棒为 4n,从而可求解.
【解答】解:由图可知:
第 1个图形需要的火柴棒根数为 4;
第 5个图形需要的火柴棒根数为 8=4×7;
第 3个图形需要的火柴棒根数为 12=4×6;
…,
则搭第 n个图形需要火柴根数为:4n,
∴第 30个图形需要的火柴棒根数为:4×30=120(根).
故答案为:120.
【点评】本题主要考查图形的变化规律,解题的关键在于通过题中图形的变化情况,通
过归纳与总结找出普遍规律求解即可.
三、计算题(共计 12 分)
21.【分析】(1)根据有理数的乘法法则计算即可;
(2)根据有理数的乘法法则计算即可;
(3)根据乘法分配律计算即可;
(4)从左到右计算即可;
(5)根据乘法分配律计算即可;
(6)根据乘法交换律和结合律计算即可.
【解答】解:(1) = ;
(2) ×24=20;
(3)2.2×( ﹣ )
=2.7× ﹣5.1×
=1.4﹣6.9
=0.8;
(4) ×
=
= ;
(5) +
= ×( )
= ×1
= ;
(6) ×34×4×
=( ×7)×(34× )
=7×4
=4.
【点评】本题考查有理数的混合运算,熟练掌握运算法则和运算顺序是解答本题的关键,
注意乘法分配律的应用.
四、操作题(共计 4 分)
22.【分析】方向角是从正北或正南方向到目标方向所形成的小于 90°的角,由此即可解答.
【解答】解:(1)荷花池在喷泉的东偏北 40°的方向上,这是以喷泉为观测点,
故答案为:喷泉;
(2)丽丽家在学校东偏北 40°方向,距离是 400m;
玲玲家在学校西偏北 40°方向,距离是 400m;
芳芳家在学校东偏南 25°方向,距离是 300m.
故答案为:40,40,东.
【点评】本题考查方向角的概念,掌握方向角的定义是解题的关键.
五、解决问题(共计 24 分)
23.【分析】根据分数乘法的意义解答即可.
【解答】解:56×(1+ )
=56×
=88(千克).
答:六年级同学收集树种 88千克.
【点评】本题考查了分数混合运算的应用,掌握分数乘法的意义是解答本题的关键.
24.【分析】先求出种黄瓜的面积,从而可求出剩下的面积,再利用所给的条件即可求解.
【解答】解:种植黄瓜的面积为:500× =200(平方米),
则剩下的面积为:500﹣200=300(平方米),
则种植西红柿的面积为:300× =240(平方米),
种植辣椒的面积为:300× =60(平方米).
答:种植黄瓜的面积为 200平方米,种植西红柿的面积为 240平方米.
【点评】本题主要考查比的应用,分数的混合运算,解答的关键是对相应的运算法则的
掌握.
25.【分析】分别求出两圆的面积,再相减即可.
【解答】解:∵两圆的半径分别为 10厘米,6厘米,
∴图中圆环(阴影部分)的面积是(102﹣72)π=64π(平方厘米),
答:图中圆环(阴影部分)的面积是 64π平方厘米.
【点评】此题主要考查了认识平面图形,正确记忆圆环的面积公式是解题关键.
26.【分析】根据题意可得到小牛的头数是大牛的头数的 80%,从而可求解.
【解答】解:小牛的头数为:
240×(1﹣20%)
=240×80%
=192(头).
答:小牛有 192头.
【点评】本题主要考查百分数的应用,解答的关键是理解清楚题意找到等量关系.
27.【分析】(1)用柳树棵数 2500除以 25%即可;
(2)用总棵数分别乘以柏树和槐树的百分比即可;
(3)用杨树的百分比减去松树的百分比即可.
【解答】解:(1)2500÷25%=10000(棵),
答:这些树苗的总数 10000棵;
(2)10000×10%=1000(棵),
10000×17%=1700(棵),
答:柏树和槐树各有 1000棵和 1700棵;
(3)(33%﹣15%)÷15%=120%,
答:杨树比松树多 120%.
【点评】本题考查扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
同课章节目录
