12.3角的平分线的性质 第一课时
文档属性
| 名称 | 12.3角的平分线的性质 第一课时 |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-18 15:57:23 | ||
图片预览




文档简介
课件18张PPT。我是射线,你是角
你常说我很公平
不偏不倚
因为我知道
你那长长的身躯里
蕴含着睿智和坚强
我要紧紧与你相随
永远做你的平分线
同学们知道我是谁吗?12.3角的平分线的性质(第一课时)新人教版 八年级数学(上册)苗馆初级中学
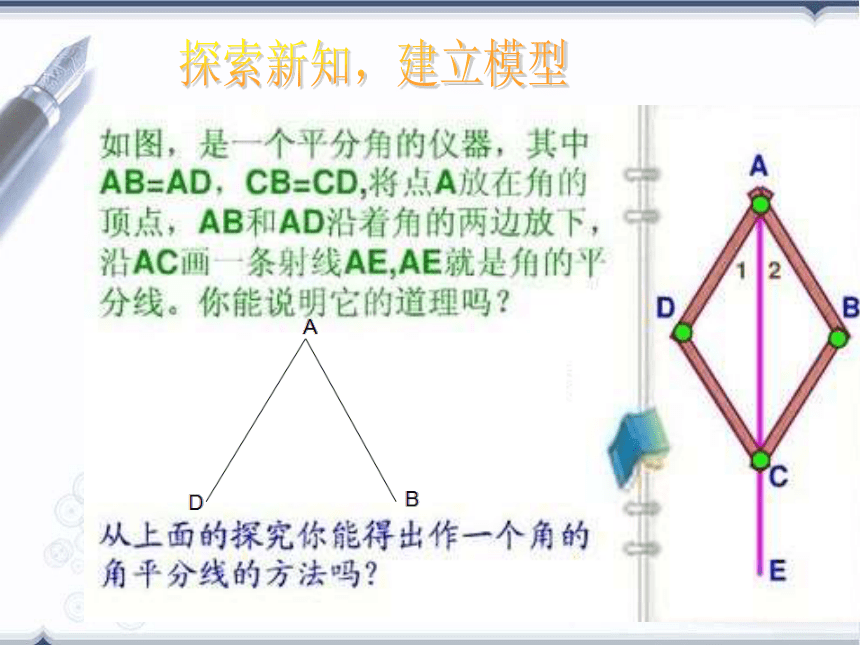
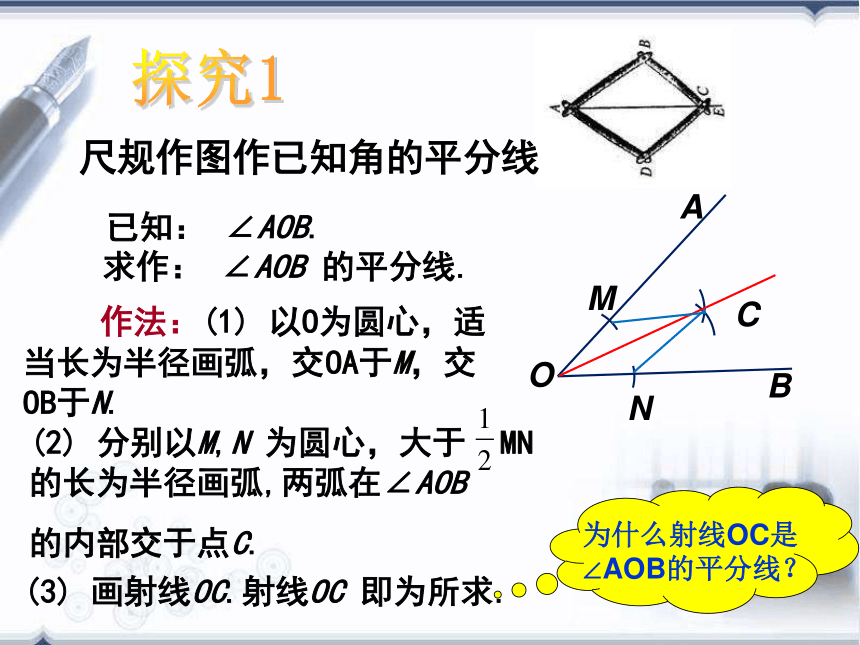
李 敬探索新知,建立模型尺规作图作已知角的平分线 已知: ∠AOB. 求作: ∠AOB 的平分线. 作法:(1) 以O为圆心,适当长为半径画弧,交OA于M,交OB于N.(3) 画射线OC.射线OC 即为所求.OCBANM探究1(2) 分别以M,N 为圆心,大于 MN的长为半径画弧,两弧在∠AOB
的内部交于点C.探究2实验如图,任意作一个角∠AOB,作出∠AOB的平分线OC.
操作探究:
1.在OC上任取一点P。
2.过点P画出OA,OB的垂线,垂足分别记为D、E。
3.测量并记录PD,PE的长度。PD=_____,PE=_____。
4.比较PD,PE的长度,你能得到什么结论?
5.组内对照,结论相同吗?
6.通过以上活动,你发现了角的平分线的什么性质?我们猜想角的平分线有什么样的性质?猜想角平分线上的点到角的两边的距离相等。命题中的题设和结论分别是什么?
思考如何用符号语言表示已知和求证.
能给出严格的证明吗?
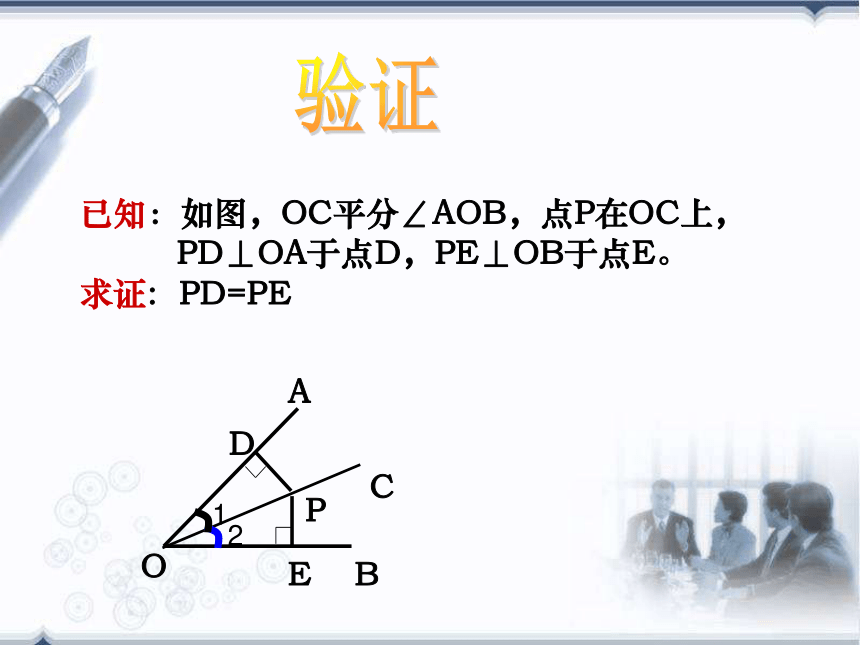
已知:如图,OC平分∠AOB,点P在OC上,
PD⊥OA于点D,PE⊥OB于点E。
求证: PD=PE验证角的平分线的性质:角平分线上的点到角的两边的距离相等。结论证明一个几何命题的步骤:反思(1)明确命题中的已知和求证;(2)根据题意,画出图形,并用数学符号表示已知和求证;(3)经过分析,找出由已知推出求证的途径,写出证明过程。 1.判断正误
(1)∵ 如图,AD平分∠BAC(已知) ∴ = , BD CD(×)应用新知 (2)∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = , BD CD(×)2.例: 如图,CD⊥AB,BE⊥AC,垂足分别为D,E, BE,CD相交于点O,∠1=∠2.
求证:OB=OC.应用新知角平分线的性质应用所具备的条件:
1.角的平分线;2.点在该平分线上;3.垂直距离;角平分线的性质的作用:判断、证明线段相等,且不需证明三角形全等例题反思角平分线上的点到角的两边距离相等畅谈收获尺规作图作角的平分线探究方法:
实验操作
猜想
验证
结论证明一个几何命题的步骤:三步1.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,则下列结论错误的是( )
OD=OE B. PD=PE
C. ∠DPO=∠EPO D. PD=OD目标检测2.已知AD是△ABC的角平分线,DE⊥AB于E, 且DE=3cm,则点D到AC的距离是( )
A. 2cm B. 3cm C. 4cm D. .6cm3.在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,
DE⊥AB,BC=7,DE=3.则BD=______基础自测4.在△OAB中,OE是它的角平分线,且EA= EB,
EC、ED分别垂直OA,OB,垂足为C,D.
求证:AC=BD.能力提升必做:课本51页习题12.3第2题
选做:课本51页习题12.3第6题作业敬请指导
你常说我很公平
不偏不倚
因为我知道
你那长长的身躯里
蕴含着睿智和坚强
我要紧紧与你相随
永远做你的平分线
同学们知道我是谁吗?12.3角的平分线的性质(第一课时)新人教版 八年级数学(上册)苗馆初级中学
李 敬探索新知,建立模型尺规作图作已知角的平分线 已知: ∠AOB. 求作: ∠AOB 的平分线. 作法:(1) 以O为圆心,适当长为半径画弧,交OA于M,交OB于N.(3) 画射线OC.射线OC 即为所求.OCBANM探究1(2) 分别以M,N 为圆心,大于 MN的长为半径画弧,两弧在∠AOB
的内部交于点C.探究2实验如图,任意作一个角∠AOB,作出∠AOB的平分线OC.
操作探究:
1.在OC上任取一点P。
2.过点P画出OA,OB的垂线,垂足分别记为D、E。
3.测量并记录PD,PE的长度。PD=_____,PE=_____。
4.比较PD,PE的长度,你能得到什么结论?
5.组内对照,结论相同吗?
6.通过以上活动,你发现了角的平分线的什么性质?我们猜想角的平分线有什么样的性质?猜想角平分线上的点到角的两边的距离相等。命题中的题设和结论分别是什么?
思考如何用符号语言表示已知和求证.
能给出严格的证明吗?
已知:如图,OC平分∠AOB,点P在OC上,
PD⊥OA于点D,PE⊥OB于点E。
求证: PD=PE验证角的平分线的性质:角平分线上的点到角的两边的距离相等。结论证明一个几何命题的步骤:反思(1)明确命题中的已知和求证;(2)根据题意,画出图形,并用数学符号表示已知和求证;(3)经过分析,找出由已知推出求证的途径,写出证明过程。 1.判断正误
(1)∵ 如图,AD平分∠BAC(已知) ∴ = , BD CD(×)应用新知 (2)∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = , BD CD(×)2.例: 如图,CD⊥AB,BE⊥AC,垂足分别为D,E, BE,CD相交于点O,∠1=∠2.
求证:OB=OC.应用新知角平分线的性质应用所具备的条件:
1.角的平分线;2.点在该平分线上;3.垂直距离;角平分线的性质的作用:判断、证明线段相等,且不需证明三角形全等例题反思角平分线上的点到角的两边距离相等畅谈收获尺规作图作角的平分线探究方法:
实验操作
猜想
验证
结论证明一个几何命题的步骤:三步1.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,则下列结论错误的是( )
OD=OE B. PD=PE
C. ∠DPO=∠EPO D. PD=OD目标检测2.已知AD是△ABC的角平分线,DE⊥AB于E, 且DE=3cm,则点D到AC的距离是( )
A. 2cm B. 3cm C. 4cm D. .6cm3.在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,
DE⊥AB,BC=7,DE=3.则BD=______基础自测4.在△OAB中,OE是它的角平分线,且EA= EB,
EC、ED分别垂直OA,OB,垂足为C,D.
求证:AC=BD.能力提升必做:课本51页习题12.3第2题
选做:课本51页习题12.3第6题作业敬请指导
