人教版五年级数学上册6.1《平行四边形的面积》课件(共25张PPT)
文档属性
| 名称 | 人教版五年级数学上册6.1《平行四边形的面积》课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 28.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 16:49:04 | ||
图片预览






文档简介
(共25张PPT)
人教版 数学 五年级 上册
多边形的面积
第2课时 小数乘整数算理
第一单元 小数乘法
平行四边形的面积
多边形的面积
第
六
单
元
第1课时
1%
2%
3%
4%
5%
6%
7%
8%
9%
10%
11%
12%
13%
14%
15%
16%
17%
18%
19%
20%
21%
22%
23%
24%
25%
26%
27%
28%
29%
30%
31%
32%
33%
34%
35%
36%
37%
38%
39%
40%
41%
42%
43%
44%
45%
46%
47%
48%
49%
50%
51%
52%
53%
54%
55%
56%
57%
58%
59%
60%
61%
62%
63%
64%
65%
66%
67%
68%
69%
70%
71%
72%
73%
74%
75%
76%
77%
78%
79%
80%
81%
82%
83%
84%
85%
86%
87%
88%
89%
90%
91%
92%
93%
94%
95%
96%
97%
98%
99%
100%
100%
LOADING
o o o
登录
登录
请输入课程章节
密码
登 录
登 录
好好学习,天天向上
平行四边形的面积
人教版 数学 五年级 上册
多边形的面积
想一想这两个花坛哪一个大呢?
想一想,说一说
要比较大小,需要求它们的面积。
我只会算长方形的…
想一想下面两个花坛哪一个大呢?
那怎么计算平行四边形的面积呢?
我们是用什么方法得出长方形的面积的计算公式的?
用数方格的方式试一试。
小组讨论
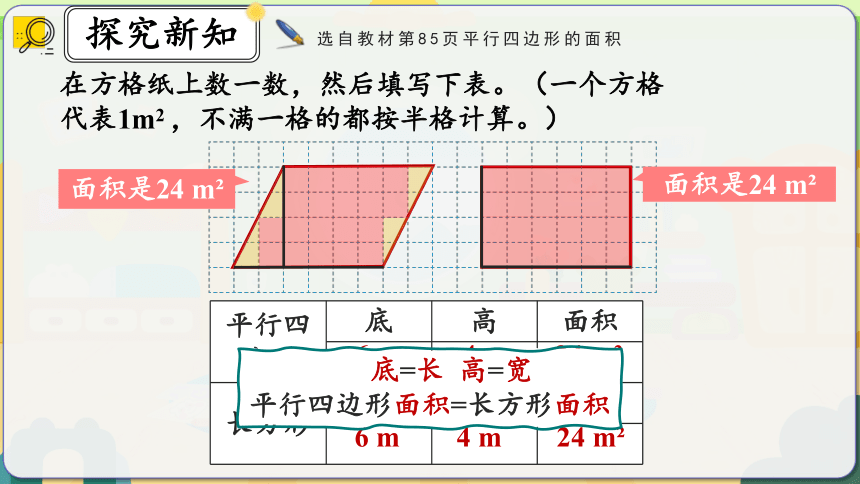
面积是24 m
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
底=长 高=宽
平行四边形面积=长方形面积
面积是24 m
在方格纸上数一数,然后填写下表。(一个方格代表1m2 ,不满一格的都按半格计算。)
选自教材第85页平行四边形的面积
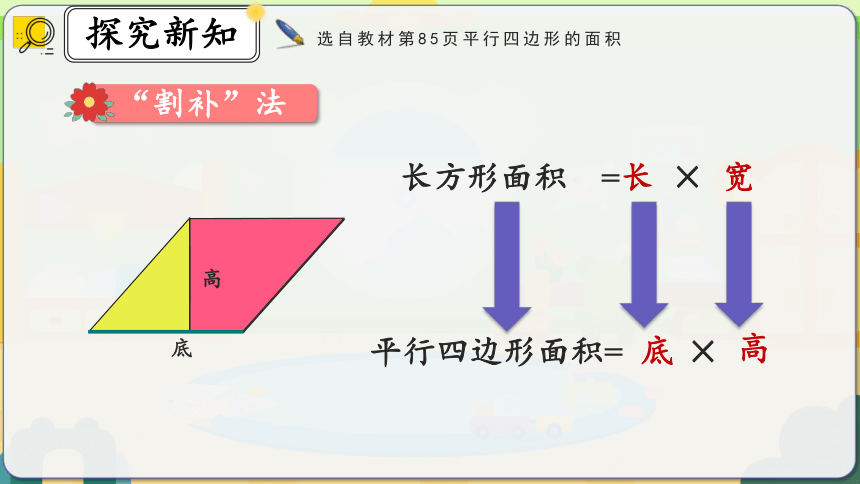
不数方格,能不能计算平行四边形的面积呢?
用“一剪一拼”的“割补”方法。
动手做一做
选自教材第85页平行四边形的面积
底
高
长方形面积 =长 × 宽
平行四边形面积=
底
高
×
“割补”法
选自教材第85页平行四边形的面积
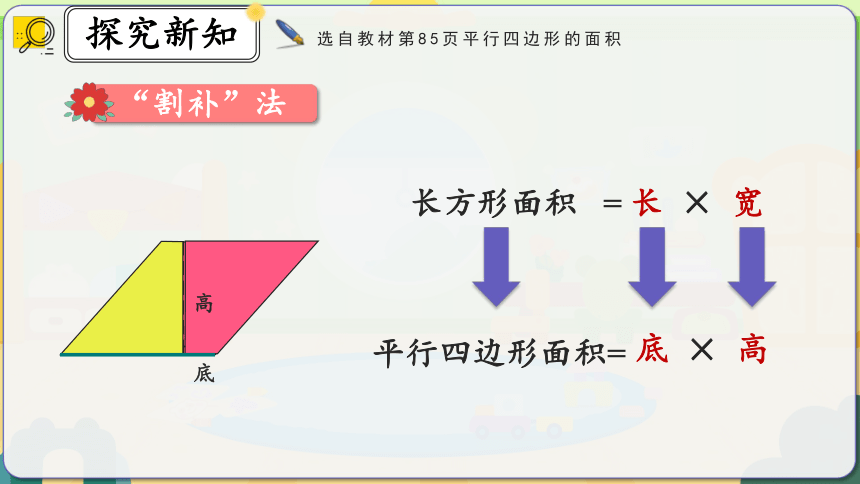
底
高
长方形面积 = 长 × 宽
平行四边形面积=
底
高
×
“割补”法
选自教材第85页平行四边形的面积
“割补”法
选自教材第85页平行四边形的面积
长方形面积 = 长 × 宽
平行四边形面积=
底
高
×
“割补”法
选自教材第85页平行四边形的面积
底
高
底
高
底
高
底
高
平行四边形的面积 = ________
底×高
底=长 高=宽
平行四边形面积=长方形面积
观察原来的平行四边形和转化后的长方形,你发现了什么?
合作讨论
选自教材第85页平行四边形的面积
如果用S表示平行四边形的面积,用a表示平
行四边形的底,用h表示平行四边形的高,那么平行四边形的面积计算公式可以写成:
S = ah
选自教材第85页平行四边形的面积
刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
合作讨论
= 6×4
……代入数求值
……加单位名称
平行四边形花坛的底是6 m,高是4 m,它的面积是多少?
S=ah ……先写字母带入公式
选自教材第86页例题一
1
填一填。
(1)把一个长方形木框拉成一个平行四边形,( )不变,它的高和面积( )。
(2)平行四边形的高不变,底扩大为原来的2倍,面积( )。
周长
改变
扩大为原来的2倍
计算下面平行四边形的面积。
S = ah
知道平行四边形的底和高,可以直接利用公式法代入进行计算
20
13
x
15 厘米
8 厘米
12 厘米
10 厘米
计算下面平行四边形的面积。
答:平行四边形的面积是120 平方厘米。
S=ah
=15×8
=120(平方厘米)
S=ah
=10×12
=120(平方厘米)
方法一
方法二
一块平行四边形的菜地,底是20 m,高是16 m,若每棵大白菜占地 0.16 m2,这块地可种多少棵大白菜
答:这块地可种 2000 棵大白菜。
20×16÷0.16 = 2000 (棵)
菜地面积÷每棵菜占地面积 = 可以种的棵数
平行四边形的面积怎么求?
S = ah
底
高
一块平行四边形的菜园,底长8.5 m,高6 m,它的面积是多少?
S = ah
知道平行四边形的底和高怎么求面积?
底
高
这节课你们都学会了哪些知识?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
S = a×h = a · h = ah
= ×
平行四边形的面积
“割补” 法
1.完成练习十九第3、6题;
2.从课时练中选取。
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
S = a×h = a · h = ah
= ×
平行四边形的面积
“割补” 法
人教版 数学 五年级 上册
多边形的面积
第2课时 小数乘整数算理
第一单元 小数乘法
平行四边形的面积
多边形的面积
第
六
单
元
第1课时
1%
2%
3%
4%
5%
6%
7%
8%
9%
10%
11%
12%
13%
14%
15%
16%
17%
18%
19%
20%
21%
22%
23%
24%
25%
26%
27%
28%
29%
30%
31%
32%
33%
34%
35%
36%
37%
38%
39%
40%
41%
42%
43%
44%
45%
46%
47%
48%
49%
50%
51%
52%
53%
54%
55%
56%
57%
58%
59%
60%
61%
62%
63%
64%
65%
66%
67%
68%
69%
70%
71%
72%
73%
74%
75%
76%
77%
78%
79%
80%
81%
82%
83%
84%
85%
86%
87%
88%
89%
90%
91%
92%
93%
94%
95%
96%
97%
98%
99%
100%
100%
LOADING
o o o
登录
登录
请输入课程章节
密码
登 录
登 录
好好学习,天天向上
平行四边形的面积
人教版 数学 五年级 上册
多边形的面积
想一想这两个花坛哪一个大呢?
想一想,说一说
要比较大小,需要求它们的面积。
我只会算长方形的…
想一想下面两个花坛哪一个大呢?
那怎么计算平行四边形的面积呢?
我们是用什么方法得出长方形的面积的计算公式的?
用数方格的方式试一试。
小组讨论
面积是24 m
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
底=长 高=宽
平行四边形面积=长方形面积
面积是24 m
在方格纸上数一数,然后填写下表。(一个方格代表1m2 ,不满一格的都按半格计算。)
选自教材第85页平行四边形的面积
不数方格,能不能计算平行四边形的面积呢?
用“一剪一拼”的“割补”方法。
动手做一做
选自教材第85页平行四边形的面积
底
高
长方形面积 =长 × 宽
平行四边形面积=
底
高
×
“割补”法
选自教材第85页平行四边形的面积
底
高
长方形面积 = 长 × 宽
平行四边形面积=
底
高
×
“割补”法
选自教材第85页平行四边形的面积
“割补”法
选自教材第85页平行四边形的面积
长方形面积 = 长 × 宽
平行四边形面积=
底
高
×
“割补”法
选自教材第85页平行四边形的面积
底
高
底
高
底
高
底
高
平行四边形的面积 = ________
底×高
底=长 高=宽
平行四边形面积=长方形面积
观察原来的平行四边形和转化后的长方形,你发现了什么?
合作讨论
选自教材第85页平行四边形的面积
如果用S表示平行四边形的面积,用a表示平
行四边形的底,用h表示平行四边形的高,那么平行四边形的面积计算公式可以写成:
S = ah
选自教材第85页平行四边形的面积
刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
合作讨论
= 6×4
……代入数求值
……加单位名称
平行四边形花坛的底是6 m,高是4 m,它的面积是多少?
S=ah ……先写字母带入公式
选自教材第86页例题一
1
填一填。
(1)把一个长方形木框拉成一个平行四边形,( )不变,它的高和面积( )。
(2)平行四边形的高不变,底扩大为原来的2倍,面积( )。
周长
改变
扩大为原来的2倍
计算下面平行四边形的面积。
S = ah
知道平行四边形的底和高,可以直接利用公式法代入进行计算
20
13
x
15 厘米
8 厘米
12 厘米
10 厘米
计算下面平行四边形的面积。
答:平行四边形的面积是120 平方厘米。
S=ah
=15×8
=120(平方厘米)
S=ah
=10×12
=120(平方厘米)
方法一
方法二
一块平行四边形的菜地,底是20 m,高是16 m,若每棵大白菜占地 0.16 m2,这块地可种多少棵大白菜
答:这块地可种 2000 棵大白菜。
20×16÷0.16 = 2000 (棵)
菜地面积÷每棵菜占地面积 = 可以种的棵数
平行四边形的面积怎么求?
S = ah
底
高
一块平行四边形的菜园,底长8.5 m,高6 m,它的面积是多少?
S = ah
知道平行四边形的底和高怎么求面积?
底
高
这节课你们都学会了哪些知识?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
S = a×h = a · h = ah
= ×
平行四边形的面积
“割补” 法
1.完成练习十九第3、6题;
2.从课时练中选取。
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
S = a×h = a · h = ah
= ×
平行四边形的面积
“割补” 法
