1.2.1排列(广东省汕尾市)
图片预览







文档简介
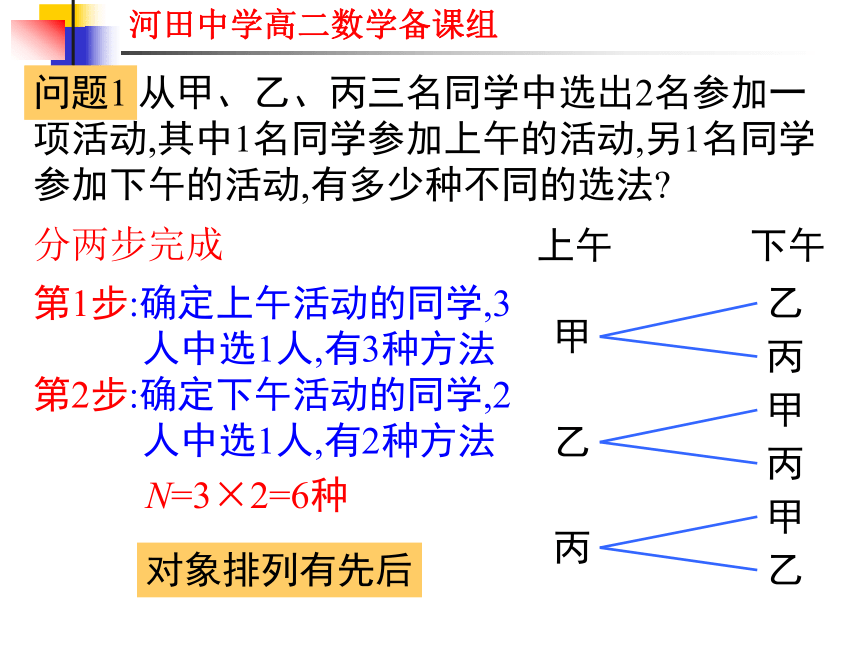
课件22张PPT。排列复习分步较多,步骤繁琐两个基本原理分类加法计数原理分步乘法计数原理问题1 从甲、乙、丙三名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?下午分两步完成第1步:确定上午活动的同学,3人中选1人,有3种方法
第2步:确定下午活动的同学,2人中选1人,有2种方法N=3×2=6种对象排列有先后元素 被取的对象从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?ab,ac,ba,bc,ca,cb共有 3×2=6 种问题转化问题2 从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?分三步完成第1步,确定百位上的数字,4个数字中任选一个,有4种方法
第2步,确定十位上的数字,剩下的3个数字中任选一个,有3种方法
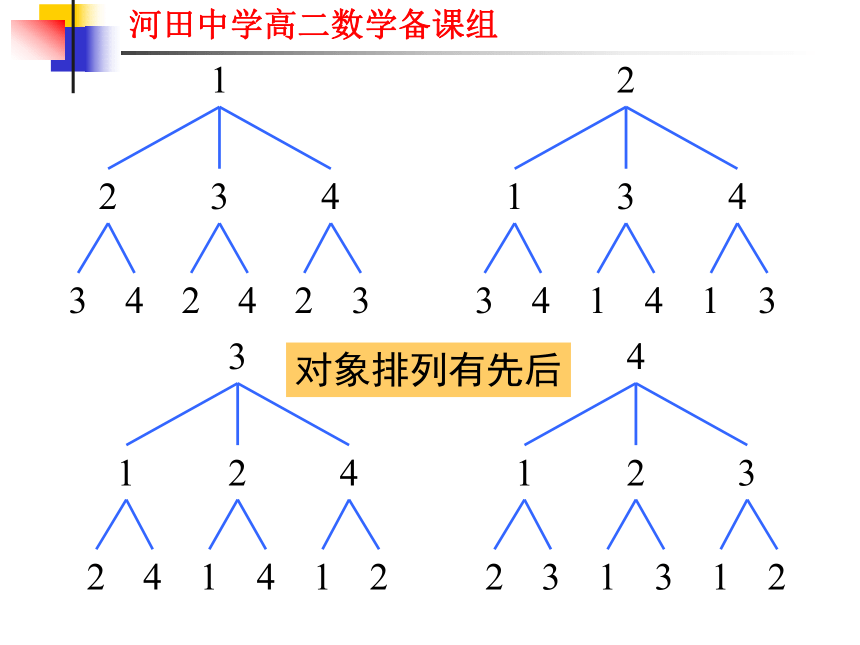
第3步,确定个位上的数学,剩下的2个数字中任选钱个,有2种方法4×3×2=24种方法对象排列有先后从4个不同的元素a,b,c,d中任取3个,然后按照一定的顺序排成一列,共有多少种不同的排列方法?abc,abd,acb,acd,adb,adc,
bac,bad,bca,bcd,bda,bdc,
cab,cad,cba,cbd,cda,cdb,
dab,dac,dba,dbc,dca,dcb.共有 4×3×2=24 种这两个问题的共
同特点是什么?问题转化排列 从n个不同的元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement). 从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,
用符号Anm表示。 当两个排列的元素完全相同,且元素的排列顺序相同称两个排列相同判断下列几个问题是不是排列问题?①从班级5名优秀团员中选出3人参加上午的团委会
②1000本参考书中选出100本给100位同学每人一本
③1000名来宾中选20名贵宾分别坐1~20号贵宾席n种(n-1)种n种(n-1)种(n-2)种n种(n-1)种(n-2)种(n-m+1)种排列数公式n,m∈N*,并且m≤n计算n个不同元素全部取出的一个排列,叫做n个元素的个全排列规定:0!=1正整数1到n的连乘积,叫做n的阶乘,记n!例 利用计算器计算: 某年全国足球甲级(A组)联赛共有14队参加,每队都要与其余各队在主客场分别比赛1次,共进行多少场比赛?①有5本不同的书,从中选出3本给3名同学,每人一本,共有多少种不同的选法?练习②有5种不同的书,从中选出3本给3名同学,每人一本,共有多少种不同的选法?排列数分步乘法计数原理练习 某段铁路上有12个车站,共需要准备多少种普通客票?每张票对应着2个车站的一个排列解 某信号兵用红,绿,蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可挂一面,二面,三面,并且不同的顺序表示不同的信号,一共可表示多少种不同的信号?练习信号分三类,
第一类为3面旗组成的信号,共A33种,
第二类为2面旗组成的信号,共A32种,
第三类为1面旗组成的信号,共A31种,
由加法原理得解N=6+6+3=16求证:练习用0~9这十个数字,可以组成多少个没有重复数字的三位数?注:0不能排在百位上分析:每一个三位数都可看成是这十个数字中任取三个数字的一个排列 解法一:百位用非零元元素先占,由乘法原理得
A91?A92=9×9×8=648(个)
解法二:把特殊元素“0”先放在满足要求的位置上:①三个数字都不为0②个位数字是0③十位数字是0;由加法原理
A93+A92+A92=9×8×7+9×8+9×8=648(个)用0~9这十个数字,可以组成多少个没有重复数字的三位数?注:0不能排在百位上分析:每一个三位数都可看成是这十个数字中任取三个数字的一个排列 解法三:先计算出10个数字任取3个数字的排列数,然后再去掉不符合要求的排列数,有
A103-A92=10×9×8-9×8=648(个)(1)直接计算法:即把符合限制条件的排列数直接计算出来,此种算法又可分为先考虑特殊元素还是先考虑特殊位置两种方法。
(2)间接计算法:即先不考虑限制条件,把所有排列种数算出。再从中减去全部不符合条件的排列种数,间接得出符合条件的排列种数。小结1.排列,全排列,阶乘的意义,排列数的阶乘形式. 2.解决排列问题的一般思路: (1)把问题分步来完成,用分步计数原理求解; (2)转化为求排列数问题来解决.作业课本习题1.2A组3,4,5,6,7
第2步:确定下午活动的同学,2人中选1人,有2种方法N=3×2=6种对象排列有先后元素 被取的对象从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?ab,ac,ba,bc,ca,cb共有 3×2=6 种问题转化问题2 从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?分三步完成第1步,确定百位上的数字,4个数字中任选一个,有4种方法
第2步,确定十位上的数字,剩下的3个数字中任选一个,有3种方法
第3步,确定个位上的数学,剩下的2个数字中任选钱个,有2种方法4×3×2=24种方法对象排列有先后从4个不同的元素a,b,c,d中任取3个,然后按照一定的顺序排成一列,共有多少种不同的排列方法?abc,abd,acb,acd,adb,adc,
bac,bad,bca,bcd,bda,bdc,
cab,cad,cba,cbd,cda,cdb,
dab,dac,dba,dbc,dca,dcb.共有 4×3×2=24 种这两个问题的共
同特点是什么?问题转化排列 从n个不同的元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement). 从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,
用符号Anm表示。 当两个排列的元素完全相同,且元素的排列顺序相同称两个排列相同判断下列几个问题是不是排列问题?①从班级5名优秀团员中选出3人参加上午的团委会
②1000本参考书中选出100本给100位同学每人一本
③1000名来宾中选20名贵宾分别坐1~20号贵宾席n种(n-1)种n种(n-1)种(n-2)种n种(n-1)种(n-2)种(n-m+1)种排列数公式n,m∈N*,并且m≤n计算n个不同元素全部取出的一个排列,叫做n个元素的个全排列规定:0!=1正整数1到n的连乘积,叫做n的阶乘,记n!例 利用计算器计算: 某年全国足球甲级(A组)联赛共有14队参加,每队都要与其余各队在主客场分别比赛1次,共进行多少场比赛?①有5本不同的书,从中选出3本给3名同学,每人一本,共有多少种不同的选法?练习②有5种不同的书,从中选出3本给3名同学,每人一本,共有多少种不同的选法?排列数分步乘法计数原理练习 某段铁路上有12个车站,共需要准备多少种普通客票?每张票对应着2个车站的一个排列解 某信号兵用红,绿,蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可挂一面,二面,三面,并且不同的顺序表示不同的信号,一共可表示多少种不同的信号?练习信号分三类,
第一类为3面旗组成的信号,共A33种,
第二类为2面旗组成的信号,共A32种,
第三类为1面旗组成的信号,共A31种,
由加法原理得解N=6+6+3=16求证:练习用0~9这十个数字,可以组成多少个没有重复数字的三位数?注:0不能排在百位上分析:每一个三位数都可看成是这十个数字中任取三个数字的一个排列 解法一:百位用非零元元素先占,由乘法原理得
A91?A92=9×9×8=648(个)
解法二:把特殊元素“0”先放在满足要求的位置上:①三个数字都不为0②个位数字是0③十位数字是0;由加法原理
A93+A92+A92=9×8×7+9×8+9×8=648(个)用0~9这十个数字,可以组成多少个没有重复数字的三位数?注:0不能排在百位上分析:每一个三位数都可看成是这十个数字中任取三个数字的一个排列 解法三:先计算出10个数字任取3个数字的排列数,然后再去掉不符合要求的排列数,有
A103-A92=10×9×8-9×8=648(个)(1)直接计算法:即把符合限制条件的排列数直接计算出来,此种算法又可分为先考虑特殊元素还是先考虑特殊位置两种方法。
(2)间接计算法:即先不考虑限制条件,把所有排列种数算出。再从中减去全部不符合条件的排列种数,间接得出符合条件的排列种数。小结1.排列,全排列,阶乘的意义,排列数的阶乘形式. 2.解决排列问题的一般思路: (1)把问题分步来完成,用分步计数原理求解; (2)转化为求排列数问题来解决.作业课本习题1.2A组3,4,5,6,7
