第2章《整式的加减》解答题专项练习(含答案)
文档属性
| 名称 | 第2章《整式的加减》解答题专项练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 654.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 15:34:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版七年级上册数学第二章整式的加减 解答题专项练习
1.化简.
(1);
(2);
(3).
2.求的值,其中,.
3.先化简,再求值:,其中,满足.
4.若a、b互为相反数,c、d互为倒数,m的绝对值为2,求的值
5.已知代数式,马小虎同学在做整式加减运算时,误将“”看成“”,计算的结果是.
(1)求代数式B.
(2)求的值.
(3)x是最大的负整数,将2代入第(2)问的结果并求值.
6.已知a,b,c在数轴上的对应点如图所示,化简:.
7.有理数在数轴上的位置如图,
(1)判断正负,用“>”或“<”填空:______0,______0,______0.
(2)化简:.
8.小马虎做一道数学题“两个多项式,,已知,试求的值”.小马虎将看成,结果答案(计算正确)为.
(1)求多项式;
(2)若多项式,且满足的结果不含项和项,求,的值.
9.已知代数式
(1)若,
①求;
②当时,求的值;
(2)若(a为常数),且A与B的和不含项,求整式的值.
10.在整式的加减练习课上,小江同学错将“”看成“”,在这种情况下小江计算的结果是.已知,请你解决下列问题:
(1)求出整式;
(2)求出正确的计算结果;
(3)若,满足,求(2)中整式的值.
11.已知,小明在计算时,误将其按计算,结果得到.
(1)求多项式B;
(2)求的正确结果是多少?
(3)若的值与x无关,则的值等于________.
12.根据题意解下列问题
(1)已知a,b互为相反数,c,d互为倒数,x的绝对值是4,求的值.
(2)定义一种新运算:.
①求的值;
②求的值.
13.小明把一张长方形纸板的四周各剪去一个同样大小的小正方形,如图所示,长方形纸板的长为a,宽为b,小正方形的边长为c.
(1)用含a、b、c的代数式表示剩余纸板(阴影部分)的面积.
(2)当时,求剩余纸板的面积.
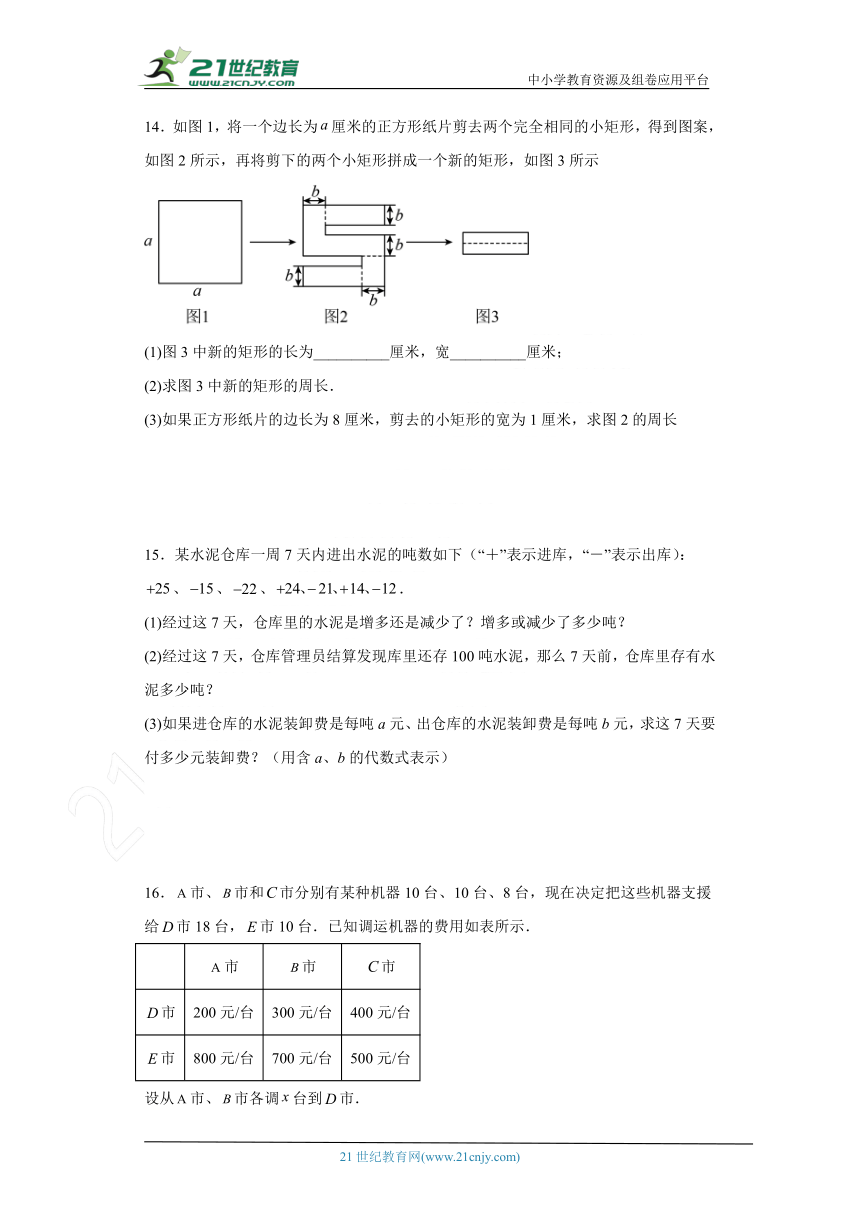
14.如图1,将一个边长为厘米的正方形纸片剪去两个完全相同的小矩形,得到图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示
(1)图3中新的矩形的长为__________厘米,宽__________厘米;
(2)求图3中新的矩形的周长.
(3)如果正方形纸片的边长为8厘米,剪去的小矩形的宽为1厘米,求图2的周长
15.某水泥仓库一周7天内进出水泥的吨数如下(“+”表示进库,“-”表示出库):
、、、.
(1)经过这7天,仓库里的水泥是增多还是减少了?增多或减少了多少吨?
(2)经过这7天,仓库管理员结算发现库里还存100吨水泥,那么7天前,仓库里存有水泥多少吨?
(3)如果进仓库的水泥装卸费是每吨a元、出仓库的水泥装卸费是每吨b元,求这7天要付多少元装卸费?(用含a、b的代数式表示)
16.市、市和市分别有某种机器10台、10台、8台,现在决定把这些机器支援给市18台,市10台.已知调运机器的费用如表所示.
市 市 市
市 200元/台 300元/台 400元/台
市 800元/台 700元/台 500元/台
设从市、市各调台到市.
(1)市调运到市的机器为______台(用含的代数式表示);
(2)市调运到市的机器的费用为______元(用含的代数式表示);
(3)求调运完毕后的总运费(用含的代数式表示,并化简).
17.某电动车厂一周计划生产2100辆电动车,平均每天计划生产300辆,由于各种原因,实际每天的生产量与计划量相比有出入.如表是某周的生产情况(超产为正减产为负).
星期 一 二 三 四 五 六 日
增减情况 +5 +13 +16
(1)本周产量最多的一天比产量最少的一天多生产电动车多少辆?
(2)根据记录可知本周共生产电动车多少辆?
(3)该厂实行每周计件工资制,每生产一辆电动车可得a元,若超额完成,则超额部分每辆再奖b元(),少生产一辆扣b元,求该厂工人这一周的工资总额.
18.某城市自来水收费实行阶梯水价,收费标准如下表所示,若某用户月份用了吨水.
月用水费 不超过吨部分 超过吨不超过吨部分 超过吨部分
收费标准 (元/吨)
(1)请分别写出,,,水费的代数式.
解:当时,水费为:___________;
当时,水费为:___________;
当时,水费为:___________.
(2)用水量为吨和吨,各需付水费多少元?
19.已知式子是关于x的二次多项式,且多项式二次项系数为b,数轴上A、B两点所对应的数分别是a,b.
(1)则 , ,,两点之间的距离 .
(2)有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度.按照如此规律不断地左右运动,当运动到2023次时,求点P所对应的有理数.
20.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为.在数轴上A、B两点之间的距离.利用数形结合思想回答下列问题:
(1)数轴上表示1和5两点之间的距离是______,数轴上表示2和的两点之间的距离为______.
(2)数轴上表示x和两点之间的距离为______,若x表示一个有理数,且,则______.
(3)利用数轴求出的最小值为______,并写出此时x可取哪些整数值______.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)
(3)
2.
3.;.
4.11或
5.(1)
(2)
(3)7
6.
7.(1),,
(2)
8.(1)
(2),
9.(1)①;②8
(2)19
10.(1)
(2)
(3)
11.(1)
(2)
(3)
12.(1)或;
(2)①;②;
13.(1)
(2)
14.(1),
(2)厘米
(3)56厘米
15.(1)减少了吨
(2)吨
(3)元
16.(1);
(2);
(3)调运完毕后的总运费为元.
17.(1)26辆
(2)2109辆
(3)()元
18.(1),,.
(2)用水量为吨和吨,各需付水费,元
19.(1),7,12;
(2)
20.(1)4;3
(2)
(3)
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版七年级上册数学第二章整式的加减 解答题专项练习
1.化简.
(1);
(2);
(3).
2.求的值,其中,.
3.先化简,再求值:,其中,满足.
4.若a、b互为相反数,c、d互为倒数,m的绝对值为2,求的值
5.已知代数式,马小虎同学在做整式加减运算时,误将“”看成“”,计算的结果是.
(1)求代数式B.
(2)求的值.
(3)x是最大的负整数,将2代入第(2)问的结果并求值.
6.已知a,b,c在数轴上的对应点如图所示,化简:.
7.有理数在数轴上的位置如图,
(1)判断正负,用“>”或“<”填空:______0,______0,______0.
(2)化简:.
8.小马虎做一道数学题“两个多项式,,已知,试求的值”.小马虎将看成,结果答案(计算正确)为.
(1)求多项式;
(2)若多项式,且满足的结果不含项和项,求,的值.
9.已知代数式
(1)若,
①求;
②当时,求的值;
(2)若(a为常数),且A与B的和不含项,求整式的值.
10.在整式的加减练习课上,小江同学错将“”看成“”,在这种情况下小江计算的结果是.已知,请你解决下列问题:
(1)求出整式;
(2)求出正确的计算结果;
(3)若,满足,求(2)中整式的值.
11.已知,小明在计算时,误将其按计算,结果得到.
(1)求多项式B;
(2)求的正确结果是多少?
(3)若的值与x无关,则的值等于________.
12.根据题意解下列问题
(1)已知a,b互为相反数,c,d互为倒数,x的绝对值是4,求的值.
(2)定义一种新运算:.
①求的值;
②求的值.
13.小明把一张长方形纸板的四周各剪去一个同样大小的小正方形,如图所示,长方形纸板的长为a,宽为b,小正方形的边长为c.
(1)用含a、b、c的代数式表示剩余纸板(阴影部分)的面积.
(2)当时,求剩余纸板的面积.
14.如图1,将一个边长为厘米的正方形纸片剪去两个完全相同的小矩形,得到图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示
(1)图3中新的矩形的长为__________厘米,宽__________厘米;
(2)求图3中新的矩形的周长.
(3)如果正方形纸片的边长为8厘米,剪去的小矩形的宽为1厘米,求图2的周长
15.某水泥仓库一周7天内进出水泥的吨数如下(“+”表示进库,“-”表示出库):
、、、.
(1)经过这7天,仓库里的水泥是增多还是减少了?增多或减少了多少吨?
(2)经过这7天,仓库管理员结算发现库里还存100吨水泥,那么7天前,仓库里存有水泥多少吨?
(3)如果进仓库的水泥装卸费是每吨a元、出仓库的水泥装卸费是每吨b元,求这7天要付多少元装卸费?(用含a、b的代数式表示)
16.市、市和市分别有某种机器10台、10台、8台,现在决定把这些机器支援给市18台,市10台.已知调运机器的费用如表所示.
市 市 市
市 200元/台 300元/台 400元/台
市 800元/台 700元/台 500元/台
设从市、市各调台到市.
(1)市调运到市的机器为______台(用含的代数式表示);
(2)市调运到市的机器的费用为______元(用含的代数式表示);
(3)求调运完毕后的总运费(用含的代数式表示,并化简).
17.某电动车厂一周计划生产2100辆电动车,平均每天计划生产300辆,由于各种原因,实际每天的生产量与计划量相比有出入.如表是某周的生产情况(超产为正减产为负).
星期 一 二 三 四 五 六 日
增减情况 +5 +13 +16
(1)本周产量最多的一天比产量最少的一天多生产电动车多少辆?
(2)根据记录可知本周共生产电动车多少辆?
(3)该厂实行每周计件工资制,每生产一辆电动车可得a元,若超额完成,则超额部分每辆再奖b元(),少生产一辆扣b元,求该厂工人这一周的工资总额.
18.某城市自来水收费实行阶梯水价,收费标准如下表所示,若某用户月份用了吨水.
月用水费 不超过吨部分 超过吨不超过吨部分 超过吨部分
收费标准 (元/吨)
(1)请分别写出,,,水费的代数式.
解:当时,水费为:___________;
当时,水费为:___________;
当时,水费为:___________.
(2)用水量为吨和吨,各需付水费多少元?
19.已知式子是关于x的二次多项式,且多项式二次项系数为b,数轴上A、B两点所对应的数分别是a,b.
(1)则 , ,,两点之间的距离 .
(2)有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度.按照如此规律不断地左右运动,当运动到2023次时,求点P所对应的有理数.
20.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为.在数轴上A、B两点之间的距离.利用数形结合思想回答下列问题:
(1)数轴上表示1和5两点之间的距离是______,数轴上表示2和的两点之间的距离为______.
(2)数轴上表示x和两点之间的距离为______,若x表示一个有理数,且,则______.
(3)利用数轴求出的最小值为______,并写出此时x可取哪些整数值______.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)
(3)
2.
3.;.
4.11或
5.(1)
(2)
(3)7
6.
7.(1),,
(2)
8.(1)
(2),
9.(1)①;②8
(2)19
10.(1)
(2)
(3)
11.(1)
(2)
(3)
12.(1)或;
(2)①;②;
13.(1)
(2)
14.(1),
(2)厘米
(3)56厘米
15.(1)减少了吨
(2)吨
(3)元
16.(1);
(2);
(3)调运完毕后的总运费为元.
17.(1)26辆
(2)2109辆
(3)()元
18.(1),,.
(2)用水量为吨和吨,各需付水费,元
19.(1),7,12;
(2)
20.(1)4;3
(2)
(3)
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
