13.3.2等边三角形 同步练习(含答案) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 13.3.2等边三角形 同步练习(含答案) 2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 321.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 21:22:13 | ||
图片预览


文档简介
13.3.2等边三角形同步练习
2023—2024学年人教版数学八年级上册
一、单选题
1.下列关于等边三角形的描述错误的是( )
A.三边相等的三角形是等边三角形
B.三个角相等的三角形是等边三角形
C.有一个角是60°的三角形是等边三角形
D.有两个角是60°的三角形是等边三角形
2.在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,以下说法错误的是( )
A.AC=2CD B.AD=2CD C.AD=3BD D.AB=2BC
3.如图所示,△ABC是等边三角形,为的中点,,垂足为.若,则△ABC的边长为( )
A.2 B.4 C.6 D.8
4.如图,在△ABC中,分别以,为边作等边三角形和等边三角形,连接,交于点,则的度数为( )
A. B. C. D.
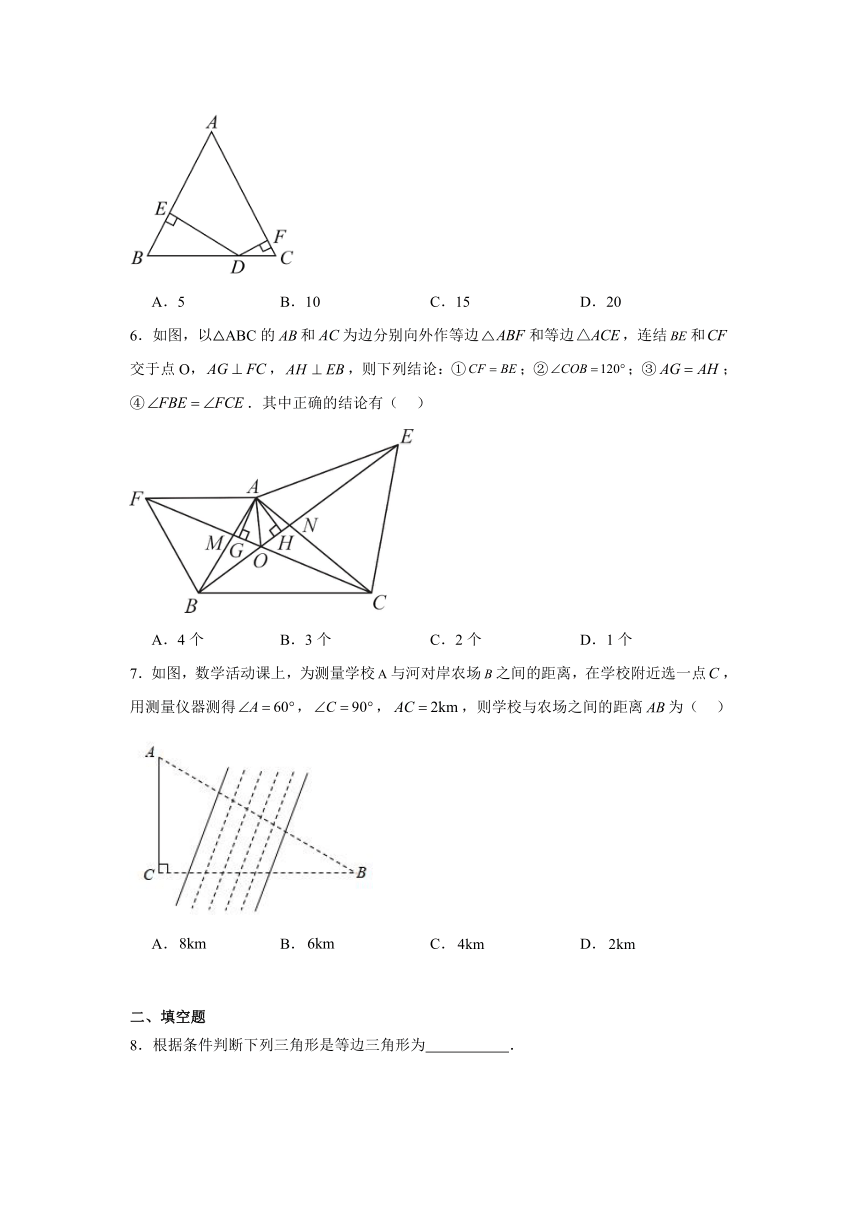
5.如图所示,△ABC是边长为20的等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=( )
A.5 B.10 C.15 D.20
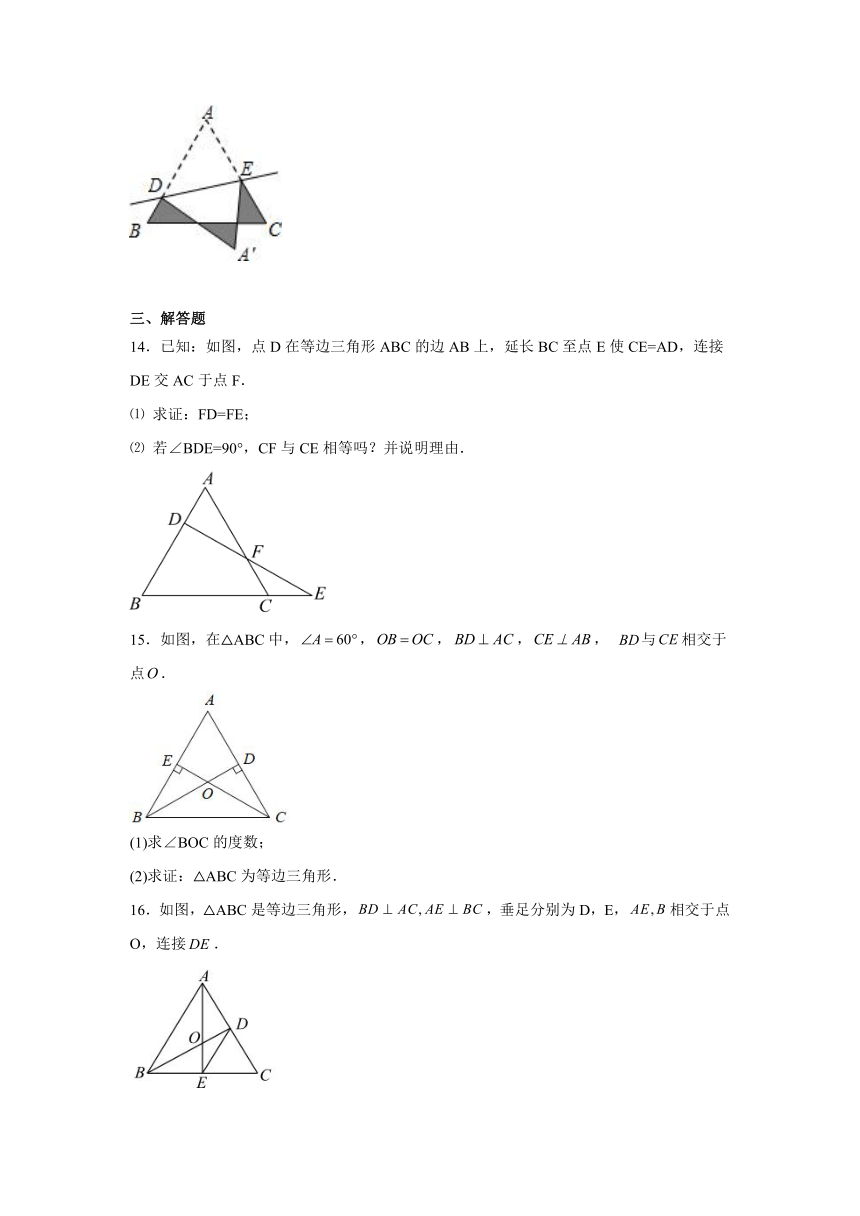
6.如图,以△ABC的和为边分别向外作等边和等边,连结和交于点O,,,则下列结论:①;②;③;④.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
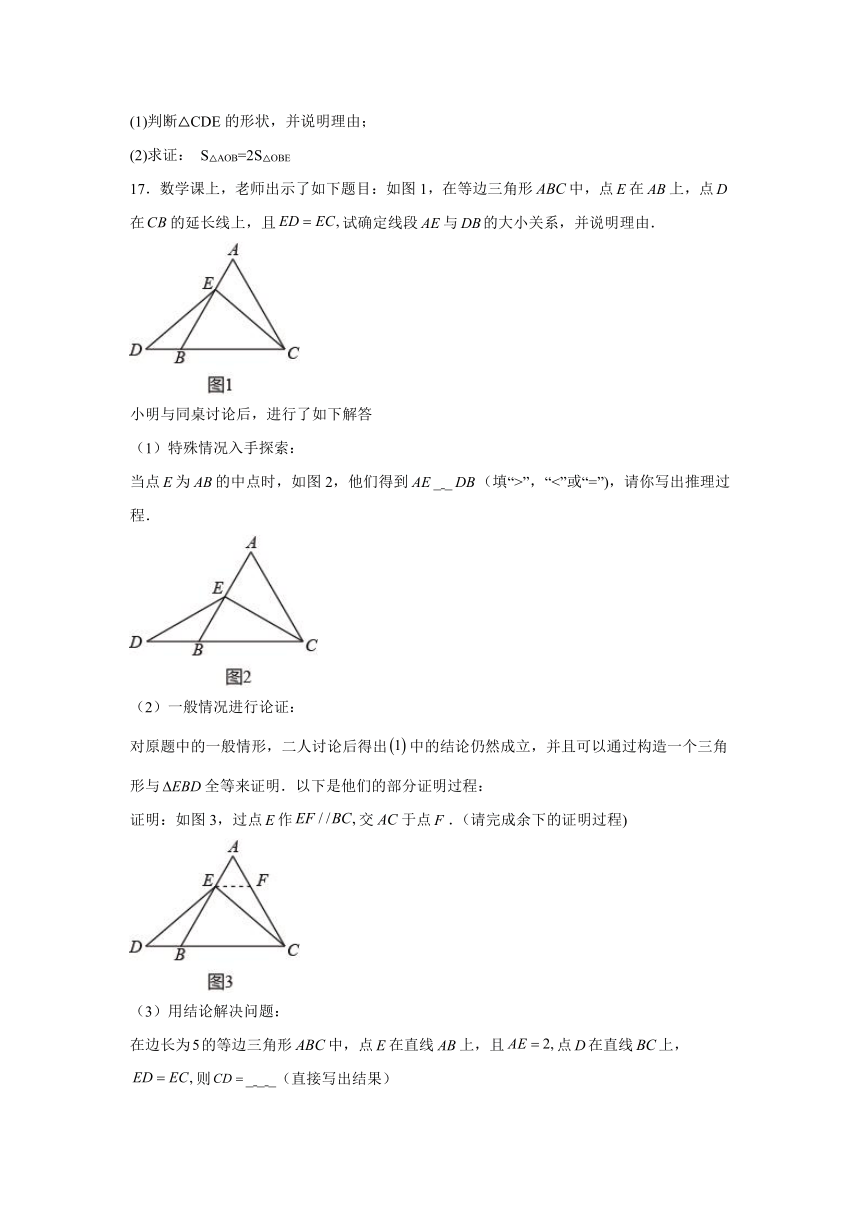
7.如图,数学活动课上,为测量学校与河对岸农场之间的距离,在学校附近选一点,用测量仪器测得,,,则学校与农场之间的距离为( )
A. B. C. D.
二、填空题
8.根据条件判断下列三角形是等边三角形为 .
9.在中,角B为90°,,,则 .
10.如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交直角两边于A,B两点,若再以A为圆心,以OA为半径画弧,与弧AB交于点C,则△AOC的形状为 .
11.如图,△ABC为等边三角形,D是△ABC 内一点,且AD=3,将△ABD绕点A旋转到△ACE的位置,连接DE,则DE的长为 .
12.在△ABC中,,,,则△ABC的周长是 .
13.如图,等边△ABC的边长为cm,、分别是、上的点,将△ADE沿直线折叠,点落在点处,且点在△ABC外部,则阴影部分图形的周长为 cm.
三、解答题
14.已知:如图,点D在等边三角形ABC的边AB上,延长BC至点E使CE=AD,连接DE交AC于点F.
⑴ 求证:FD=FE;
⑵ 若∠BDE=90°,CF与CE相等吗?并说明理由.
15.如图,在△ABC中,,,,, 与相交于点.
(1)求∠BOC的度数;
(2)求证:△ABC为等边三角形.
16.如图,△ABC是等边三角形,,垂足分别为D,E,相交于点O,连接.
(1)判断△CDE的形状,并说明理由;
(2)求证: S△AOB=2S△OBE
17.数学课上,老师出示了如下题目:如图1,在等边三角形中,点在上,点在的延长线上,且试确定线段与的大小关系,并说明理由.
小明与同桌讨论后,进行了如下解答
(1)特殊情况入手探索:
当点为的中点时,如图2,他们得到_ _(填“>”,“<”或“=”),请你写出推理过程.
(2)一般情况进行论证:
对原题中的一般情形,二人讨论后得出中的结论仍然成立,并且可以通过构造一个三角形与全等来证明.以下是他们的部分证明过程:
证明:如图3,过点作交于点.(请完成余下的证明过程)
(3)用结论解决问题:
在边长为的等边三角形中,点在直线上,且点在直线上,则_ _ _(直接写出结果)
18.四边形ACBD是由等边△ABC和顶角为120°的等腰△ABD拼成,将一个60°角顶点放在D处,将60°角绕D点旋转,该60°角两边分别交直线BC、AC于M、N.交直线AB于E、F两点,
(1)当E、F分别在边AB上时(如图1),求证:BM+AN=MN;
(2)当E、F分别在边BA的延长线上时如图2,求线段BM、AN、MN之间又有怎样的数量关系?并说明理由.
(3)在(1)的条件下,若AC=5,AE=1,求BM的长.
参考答案:
1.C
2.B
3.B
4.B
5.B
6.B
7.C
8.(2)(3)(5)(6)
9.5
10.等边三角形.
11.3.
12.12
13.6
14.(1)过点D作DG∥BC交AC于点G,根据全等三角形的判定证得△DGF≌△ECF (ASA)即可求证结论;
(2)根据等边三角形的性质和三角形内角和求得∠ABC=60°,∠BED=30°,根据三角形外角的性质可得∠CFE=30°,继而根据等角对等边的性质求解.
15.(1)
(2)求出,可得,即可证明△ABC为等边三角形.
16.(1)∵△ABC是等边三角形,且BD⊥AC,AE⊥BC,
∴∠C=60°,CE=BC,CD=AC;而BC=AC,
∴CD=CE,
∴△CDE是等边三角形.
(2)由(1)知:AE、BD分别是△ABC的中线,
∴∠BAE=∠DBA=30°,AE⊥CB,
∴OA=OB,
∵∠OBE=30°,
∴OB=2OE,
∴AO=2OE,
∵若△AOB以OA为底,△OBE以OE为底,则它们是同高的,
∴S△AOB:S△OBE ,
∴S△AOB=2S△OBE
17.解:(1)=
(2)如图3,
∵△ABC为等边三角形,且EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,∠FEC=∠ECB;
∴∠EFC=∠DBE=120°;
∵ED=EC,
∴∠D=∠ECB,∠D=∠FEC,
在△EFC与△DBE中,
∴△EFC≌△DBE(AAS),
∴EF=DB;
∵∠AEF=∠AFE=60°
∴△AEF为等边三角形,
∴AE=EF,
∴AE=BD.
(3)7或3.
18.(1)证明:把△DBM绕点D逆时针旋转120°得到△DAQ,
则DM=DQ,AQ=BM,∠ADQ=∠BDM,
∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD-∠MDN=120°-60°=60°,
∴∠QDN=∠MDN=60°,
∵在△MND和△QND中,,
∴△MND≌△QND(SAS),
∴MN=QN,
∵QN=AQ+AN=BM+AN,
∴BM+AN=MN;
(2)MN+AN=BM.
理由如下:如图,把△DAN绕点D顺时针旋转120°得到△DBP,
则DN=DP,AN=BP,
∵∠DAN=∠DBP=90°,
∴点P在BM上,
∵∠MDP=∠ADB-∠ADM-∠BDP=120°-∠ADM-∠ADN=120°-∠MDN=120°-60°=60°,
∴∠MDP=∠MDN=60°,
∵在△MND和△MPD中,,
∴△MND≌△MPD(SAS),
∴MN=MP,
∵BM=MP+BP,
∴MN+AN=BM;
(3)如图,过点M作MH∥AC交AB于G,交DN于H,
∵△ABC是等边三角形,
∴△BMG是等边三角形,
∴BM=MG=BG,
根据(1)△MND≌△QND可得∠QND=∠MND,
根据MH∥AC可得∠QND=∠MHN,
∴∠MND=∠MHN,
∴MN=MH,
∴GH=MH-MG=MN-BM=AN,
即AN=GH,
∵在△ANE和△GHE中,,
∴△ANE≌△GHE(AAS),
∴AE=EG=1,
∵AC=5,
∴AB=AC=5,
∴BG=AB-AE-EG=5-1-1=3,
∴BM=BG=3.
2023—2024学年人教版数学八年级上册
一、单选题
1.下列关于等边三角形的描述错误的是( )
A.三边相等的三角形是等边三角形
B.三个角相等的三角形是等边三角形
C.有一个角是60°的三角形是等边三角形
D.有两个角是60°的三角形是等边三角形
2.在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,以下说法错误的是( )
A.AC=2CD B.AD=2CD C.AD=3BD D.AB=2BC
3.如图所示,△ABC是等边三角形,为的中点,,垂足为.若,则△ABC的边长为( )
A.2 B.4 C.6 D.8
4.如图,在△ABC中,分别以,为边作等边三角形和等边三角形,连接,交于点,则的度数为( )
A. B. C. D.
5.如图所示,△ABC是边长为20的等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=( )
A.5 B.10 C.15 D.20
6.如图,以△ABC的和为边分别向外作等边和等边,连结和交于点O,,,则下列结论:①;②;③;④.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
7.如图,数学活动课上,为测量学校与河对岸农场之间的距离,在学校附近选一点,用测量仪器测得,,,则学校与农场之间的距离为( )
A. B. C. D.
二、填空题
8.根据条件判断下列三角形是等边三角形为 .
9.在中,角B为90°,,,则 .
10.如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交直角两边于A,B两点,若再以A为圆心,以OA为半径画弧,与弧AB交于点C,则△AOC的形状为 .
11.如图,△ABC为等边三角形,D是△ABC 内一点,且AD=3,将△ABD绕点A旋转到△ACE的位置,连接DE,则DE的长为 .
12.在△ABC中,,,,则△ABC的周长是 .
13.如图,等边△ABC的边长为cm,、分别是、上的点,将△ADE沿直线折叠,点落在点处,且点在△ABC外部,则阴影部分图形的周长为 cm.
三、解答题
14.已知:如图,点D在等边三角形ABC的边AB上,延长BC至点E使CE=AD,连接DE交AC于点F.
⑴ 求证:FD=FE;
⑵ 若∠BDE=90°,CF与CE相等吗?并说明理由.
15.如图,在△ABC中,,,,, 与相交于点.
(1)求∠BOC的度数;
(2)求证:△ABC为等边三角形.
16.如图,△ABC是等边三角形,,垂足分别为D,E,相交于点O,连接.
(1)判断△CDE的形状,并说明理由;
(2)求证: S△AOB=2S△OBE
17.数学课上,老师出示了如下题目:如图1,在等边三角形中,点在上,点在的延长线上,且试确定线段与的大小关系,并说明理由.
小明与同桌讨论后,进行了如下解答
(1)特殊情况入手探索:
当点为的中点时,如图2,他们得到_ _(填“>”,“<”或“=”),请你写出推理过程.
(2)一般情况进行论证:
对原题中的一般情形,二人讨论后得出中的结论仍然成立,并且可以通过构造一个三角形与全等来证明.以下是他们的部分证明过程:
证明:如图3,过点作交于点.(请完成余下的证明过程)
(3)用结论解决问题:
在边长为的等边三角形中,点在直线上,且点在直线上,则_ _ _(直接写出结果)
18.四边形ACBD是由等边△ABC和顶角为120°的等腰△ABD拼成,将一个60°角顶点放在D处,将60°角绕D点旋转,该60°角两边分别交直线BC、AC于M、N.交直线AB于E、F两点,
(1)当E、F分别在边AB上时(如图1),求证:BM+AN=MN;
(2)当E、F分别在边BA的延长线上时如图2,求线段BM、AN、MN之间又有怎样的数量关系?并说明理由.
(3)在(1)的条件下,若AC=5,AE=1,求BM的长.
参考答案:
1.C
2.B
3.B
4.B
5.B
6.B
7.C
8.(2)(3)(5)(6)
9.5
10.等边三角形.
11.3.
12.12
13.6
14.(1)过点D作DG∥BC交AC于点G,根据全等三角形的判定证得△DGF≌△ECF (ASA)即可求证结论;
(2)根据等边三角形的性质和三角形内角和求得∠ABC=60°,∠BED=30°,根据三角形外角的性质可得∠CFE=30°,继而根据等角对等边的性质求解.
15.(1)
(2)求出,可得,即可证明△ABC为等边三角形.
16.(1)∵△ABC是等边三角形,且BD⊥AC,AE⊥BC,
∴∠C=60°,CE=BC,CD=AC;而BC=AC,
∴CD=CE,
∴△CDE是等边三角形.
(2)由(1)知:AE、BD分别是△ABC的中线,
∴∠BAE=∠DBA=30°,AE⊥CB,
∴OA=OB,
∵∠OBE=30°,
∴OB=2OE,
∴AO=2OE,
∵若△AOB以OA为底,△OBE以OE为底,则它们是同高的,
∴S△AOB:S△OBE ,
∴S△AOB=2S△OBE
17.解:(1)=
(2)如图3,
∵△ABC为等边三角形,且EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,∠FEC=∠ECB;
∴∠EFC=∠DBE=120°;
∵ED=EC,
∴∠D=∠ECB,∠D=∠FEC,
在△EFC与△DBE中,
∴△EFC≌△DBE(AAS),
∴EF=DB;
∵∠AEF=∠AFE=60°
∴△AEF为等边三角形,
∴AE=EF,
∴AE=BD.
(3)7或3.
18.(1)证明:把△DBM绕点D逆时针旋转120°得到△DAQ,
则DM=DQ,AQ=BM,∠ADQ=∠BDM,
∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD-∠MDN=120°-60°=60°,
∴∠QDN=∠MDN=60°,
∵在△MND和△QND中,,
∴△MND≌△QND(SAS),
∴MN=QN,
∵QN=AQ+AN=BM+AN,
∴BM+AN=MN;
(2)MN+AN=BM.
理由如下:如图,把△DAN绕点D顺时针旋转120°得到△DBP,
则DN=DP,AN=BP,
∵∠DAN=∠DBP=90°,
∴点P在BM上,
∵∠MDP=∠ADB-∠ADM-∠BDP=120°-∠ADM-∠ADN=120°-∠MDN=120°-60°=60°,
∴∠MDP=∠MDN=60°,
∵在△MND和△MPD中,,
∴△MND≌△MPD(SAS),
∴MN=MP,
∵BM=MP+BP,
∴MN+AN=BM;
(3)如图,过点M作MH∥AC交AB于G,交DN于H,
∵△ABC是等边三角形,
∴△BMG是等边三角形,
∴BM=MG=BG,
根据(1)△MND≌△QND可得∠QND=∠MND,
根据MH∥AC可得∠QND=∠MHN,
∴∠MND=∠MHN,
∴MN=MH,
∴GH=MH-MG=MN-BM=AN,
即AN=GH,
∵在△ANE和△GHE中,,
∴△ANE≌△GHE(AAS),
∴AE=EG=1,
∵AC=5,
∴AB=AC=5,
∴BG=AB-AE-EG=5-1-1=3,
∴BM=BG=3.
