第三章函数课时训练(广东省深圳市)无答案
文档属性
| 名称 | 第三章函数课时训练(广东省深圳市)无答案 |

|
|
| 格式 | rar | ||
| 文件大小 | 51.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-04 00:00:00 | ||
图片预览


文档简介
第三章函数
第1课时变量与图象
1、函数中自变量的取值范围是 。
2、函数中自变量的取值范围是( )
A、≠3,≠-2 B、≥且≠3
C、≤且≠-2 D、<<3
3、假定甲、乙两人在一次赛跑中,路程与时间的关系如图所示,则:
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)乙在这次赛跑中的速度为 米/秒。
第二课时
4、由化学知识知氯酸钾加热到一定温度可放出氧气,而二氧化锰加热不能放出氧气。今有质量相等的两份氯酸钾、,中一份混有少量二氧化锰,分别同时加热,放出氧化的质量与加热时间的关系图象,正确的是( )
A B C D
第2课时函数与图象
1、点A(x,y)是平面直角坐标系中的一点,若xy<0,则点A在 象限;若x=0则点A在 ;若x<0,y≠0则点A在 ; 若xy>0,且x=y, 则点A在
2、已知点P(a,b),a·b>0,a+b<0,则点P在( )
(A) 第一象限(B)第二象限 (C)第三象限 (D)第四象限
3、在直角坐标系中,点P(-1,-)关于x轴对称的点的坐标是( )
(A)(-1,-)(B)(1,-)(C)(1,)(D)(-1,)
3、某市自来水公司为了鼓励市民节约用水,采取分段收费标准,若某户居民每月应交水费(元)是用水量(吨)的函数,其图象如图所示。
(1)分别写出≤5和>5时,与之间的函数解析式 ;
(2)观察函数的图象,利用函数的解析式,回答自来水公司采取的收费标准是:
。
(3)若某户居民该月用水3.5吨,则应交水费 元;若该月交水费9元,则用水 吨。
4、在有序实数对(3,-20), (-4,1), (,3), (5, )中,在函数y=x+3的图象上的点
有 个
6、已知点A(a,b), B(a,-b), 那么点A,B关于 对称,直线AB平行于 轴
7、点P(-4,-7)到x轴的距离为 ,到y轴的距离为 ,到原点距离为
8、已知P是第二象限内坐标轴夹角平分线上一点,点P到原点距离为4,那么点P坐标为
9、菱形边长为6,一个内角为120°,它的对角线与两坐标轴重合,则菱形四个顶点的坐标分别是
10、在直角坐标系中,点P(-1,-)关于x轴对称的点的坐标是( )
(A)(-1,-)(B)(1,-)(C)(1,)(D)(-1,)
11、已知点P(x,y)的坐标满足方程|x+1|+=0,则点P在( )
(A) 第一象限(B)第二象限 (C)第三象限 (D)第四象限
第3课时一次函数
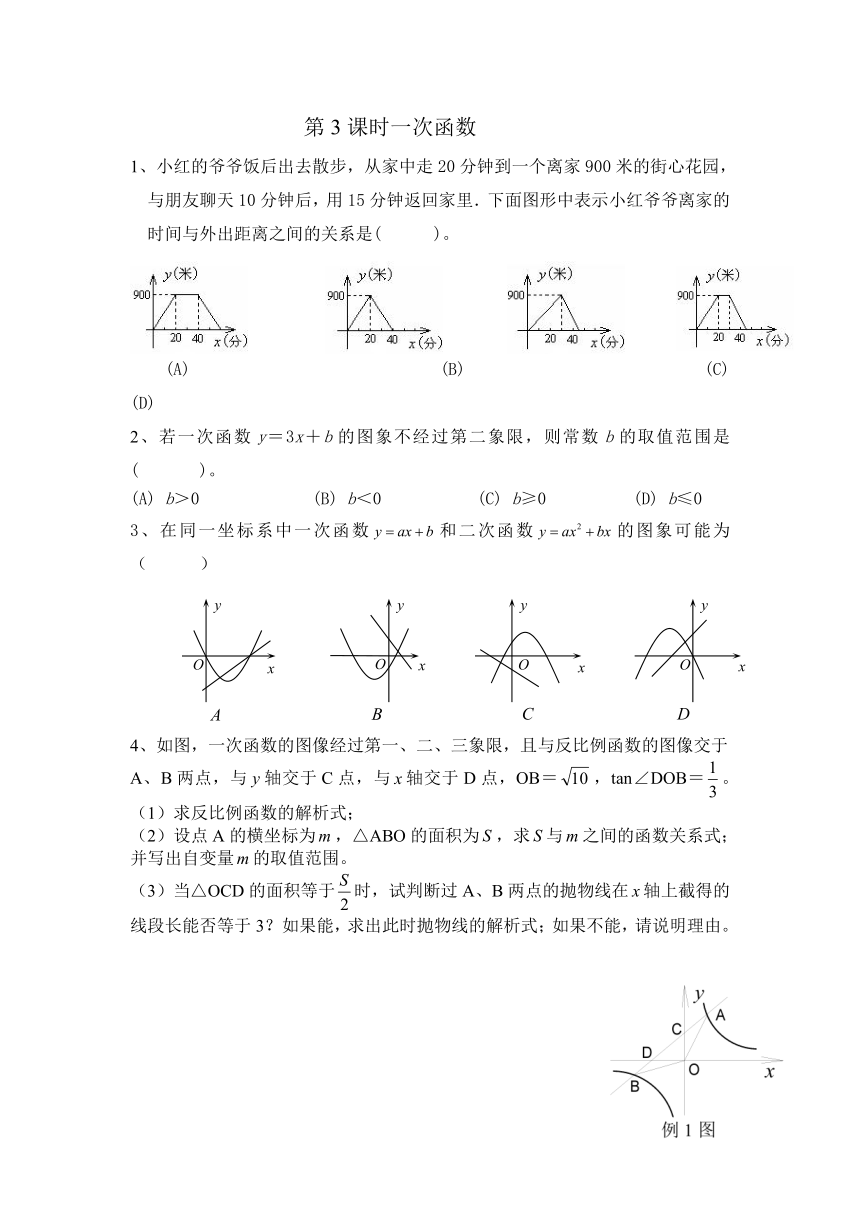
1、小红的爷爷饭后出去散步,从家中走20分钟到一个离家900米的街心花园,与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家的时间与外出距离之间的关系是( )。
(A) (B) (C) (D)
2、若一次函数y=3x+b的图象不经过第二象限,则常数b的取值范围是( )。
(A) b>0 (B) b<0 (C) b≥0 (D) b≤0
3、在同一坐标系中一次函数和二次函数的图象可能为( )
4、如图,一次函数的图像经过第一、二、三象限,且与反比例函数的图像交于A、B两点,与轴交于C点,与轴交于D点,OB=,tan∠DOB=。(1)求反比例函数的解析式;
(2)设点A的横坐标为,△ABO的面积为,求与之间的函数关系式;并写出自变量的取值范围。
(3)当△OCD的面积等于时,试判断过A、B两点的抛物线在轴上截得的线段长能否等于3?如果能,求出此时抛物线的解析式;如果不能,请说明理由。
第4课时反比例函数
1、(河南)如图,函数图象①、②、③的 表达式应为( ).
(A) y=-,y=x+2,y=-;
(B) y=,y=-x+2,y=;
(C) y=-,y=x-2,y=;
(D) y=-,y=x-2,y=-;
2、已知M、N两点关于轴对称,且点M在双曲线上,点N在直线上, 设点M(,),则抛物线的顶点坐标为 。
第5课时二次函数
1、若抛物线的顶点在第二象限,则常数的取值范围是( )
A、或 B、
C、 D、
2、函数的图像与轴有且只有一个交点,那么的值是 ,与轴的交点坐标为 。
3、把抛物线的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是 ( )
A. B.
C. D.
3、某商人将进货单价为8元的商品按每件10元出售,每天可销售100件,现在他采用提高售出价,减少进货量的办法增加利润,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销价提高( )
A、8元或10元 B、12元 C、8元 D、10元
4、(扬州)如图,抛物线的对称轴是直线,它与轴交于、两点,与轴交于点.点、的坐标分别是、.
(1) 求此抛物线对应的函数解析式;
(1) 若点是抛物线上位于轴上方的一个动点,求△面积的最大值.
第6课时函数的应用
1、某批发商欲将一批海产品由A地运往B地,汽车货运公司和铁路货运公司均开办海产品运输业务。已知运输路程为120千米,汽车和火车的速度分别为60千米/时,100千米/时。两货运公司的收费项目及收费标准如下表所示:
运输工具 运输费单价(元/吨·千米) 冷藏费单价(元/吨·小时) 过路费(元) 装卸及管理费(元)
汽车 2 5 200 0
火车 1.8 5 0 1600
(1)设该批发商待运的海产品有吨,汽车货运公司和铁路货运公司所要收取的费用分别为元、元,试求、与之间的函数关系式;
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应该选择哪个货运公司承担运输业务?
2、(河北)某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产.已知生产每件产品的成本为40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为元,年销售量为万件,年获利(年获利=年销售额-生产成本-投资)万元.
(1)试写出与之间的函数关系式;(不必写出的取值范围)
(2)试写出与之间的函数关系式;(不必写出的取值范围)
(3)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?相应的年销售量分别为多少万件?
(4)公司计划:在第一年按年获利最大确定的销售单价进行销售,第二年年获利不低于1130万元.请你借助函数的大致图象说明,第二年的销售单价(元)应确定在什么范围内?
3、某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克元,月销售利润为元,求与之间的函数关系式(不必写出自变量的取值范围);
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(4)商店要想月销售利润最大,销售单价应定为多少元?最大月销售利润是多少?
O
x
y
O
x
y
O
x
y
O
x
y
A
B
C
D
第1课时变量与图象
1、函数中自变量的取值范围是 。
2、函数中自变量的取值范围是( )
A、≠3,≠-2 B、≥且≠3
C、≤且≠-2 D、<<3
3、假定甲、乙两人在一次赛跑中,路程与时间的关系如图所示,则:
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)乙在这次赛跑中的速度为 米/秒。
第二课时
4、由化学知识知氯酸钾加热到一定温度可放出氧气,而二氧化锰加热不能放出氧气。今有质量相等的两份氯酸钾、,中一份混有少量二氧化锰,分别同时加热,放出氧化的质量与加热时间的关系图象,正确的是( )
A B C D
第2课时函数与图象
1、点A(x,y)是平面直角坐标系中的一点,若xy<0,则点A在 象限;若x=0则点A在 ;若x<0,y≠0则点A在 ; 若xy>0,且x=y, 则点A在
2、已知点P(a,b),a·b>0,a+b<0,则点P在( )
(A) 第一象限(B)第二象限 (C)第三象限 (D)第四象限
3、在直角坐标系中,点P(-1,-)关于x轴对称的点的坐标是( )
(A)(-1,-)(B)(1,-)(C)(1,)(D)(-1,)
3、某市自来水公司为了鼓励市民节约用水,采取分段收费标准,若某户居民每月应交水费(元)是用水量(吨)的函数,其图象如图所示。
(1)分别写出≤5和>5时,与之间的函数解析式 ;
(2)观察函数的图象,利用函数的解析式,回答自来水公司采取的收费标准是:
。
(3)若某户居民该月用水3.5吨,则应交水费 元;若该月交水费9元,则用水 吨。
4、在有序实数对(3,-20), (-4,1), (,3), (5, )中,在函数y=x+3的图象上的点
有 个
6、已知点A(a,b), B(a,-b), 那么点A,B关于 对称,直线AB平行于 轴
7、点P(-4,-7)到x轴的距离为 ,到y轴的距离为 ,到原点距离为
8、已知P是第二象限内坐标轴夹角平分线上一点,点P到原点距离为4,那么点P坐标为
9、菱形边长为6,一个内角为120°,它的对角线与两坐标轴重合,则菱形四个顶点的坐标分别是
10、在直角坐标系中,点P(-1,-)关于x轴对称的点的坐标是( )
(A)(-1,-)(B)(1,-)(C)(1,)(D)(-1,)
11、已知点P(x,y)的坐标满足方程|x+1|+=0,则点P在( )
(A) 第一象限(B)第二象限 (C)第三象限 (D)第四象限
第3课时一次函数
1、小红的爷爷饭后出去散步,从家中走20分钟到一个离家900米的街心花园,与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家的时间与外出距离之间的关系是( )。
(A) (B) (C) (D)
2、若一次函数y=3x+b的图象不经过第二象限,则常数b的取值范围是( )。
(A) b>0 (B) b<0 (C) b≥0 (D) b≤0
3、在同一坐标系中一次函数和二次函数的图象可能为( )
4、如图,一次函数的图像经过第一、二、三象限,且与反比例函数的图像交于A、B两点,与轴交于C点,与轴交于D点,OB=,tan∠DOB=。(1)求反比例函数的解析式;
(2)设点A的横坐标为,△ABO的面积为,求与之间的函数关系式;并写出自变量的取值范围。
(3)当△OCD的面积等于时,试判断过A、B两点的抛物线在轴上截得的线段长能否等于3?如果能,求出此时抛物线的解析式;如果不能,请说明理由。
第4课时反比例函数
1、(河南)如图,函数图象①、②、③的 表达式应为( ).
(A) y=-,y=x+2,y=-;
(B) y=,y=-x+2,y=;
(C) y=-,y=x-2,y=;
(D) y=-,y=x-2,y=-;
2、已知M、N两点关于轴对称,且点M在双曲线上,点N在直线上, 设点M(,),则抛物线的顶点坐标为 。
第5课时二次函数
1、若抛物线的顶点在第二象限,则常数的取值范围是( )
A、或 B、
C、 D、
2、函数的图像与轴有且只有一个交点,那么的值是 ,与轴的交点坐标为 。
3、把抛物线的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是 ( )
A. B.
C. D.
3、某商人将进货单价为8元的商品按每件10元出售,每天可销售100件,现在他采用提高售出价,减少进货量的办法增加利润,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销价提高( )
A、8元或10元 B、12元 C、8元 D、10元
4、(扬州)如图,抛物线的对称轴是直线,它与轴交于、两点,与轴交于点.点、的坐标分别是、.
(1) 求此抛物线对应的函数解析式;
(1) 若点是抛物线上位于轴上方的一个动点,求△面积的最大值.
第6课时函数的应用
1、某批发商欲将一批海产品由A地运往B地,汽车货运公司和铁路货运公司均开办海产品运输业务。已知运输路程为120千米,汽车和火车的速度分别为60千米/时,100千米/时。两货运公司的收费项目及收费标准如下表所示:
运输工具 运输费单价(元/吨·千米) 冷藏费单价(元/吨·小时) 过路费(元) 装卸及管理费(元)
汽车 2 5 200 0
火车 1.8 5 0 1600
(1)设该批发商待运的海产品有吨,汽车货运公司和铁路货运公司所要收取的费用分别为元、元,试求、与之间的函数关系式;
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应该选择哪个货运公司承担运输业务?
2、(河北)某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产.已知生产每件产品的成本为40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为元,年销售量为万件,年获利(年获利=年销售额-生产成本-投资)万元.
(1)试写出与之间的函数关系式;(不必写出的取值范围)
(2)试写出与之间的函数关系式;(不必写出的取值范围)
(3)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?相应的年销售量分别为多少万件?
(4)公司计划:在第一年按年获利最大确定的销售单价进行销售,第二年年获利不低于1130万元.请你借助函数的大致图象说明,第二年的销售单价(元)应确定在什么范围内?
3、某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克元,月销售利润为元,求与之间的函数关系式(不必写出自变量的取值范围);
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(4)商店要想月销售利润最大,销售单价应定为多少元?最大月销售利润是多少?
O
x
y
O
x
y
O
x
y
O
x
y
A
B
C
D
