4.4.2对数函数的图象和性质(第一课时)
文档属性
| 名称 | 4.4.2对数函数的图象和性质(第一课时) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 13:35:39 | ||
图片预览





文档简介
(共29张PPT)
第4章 指数函数与对数函数
4.4 对数函数
4.4.2 对数函数的图象和性质(第一课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.通过用描点法画具体对数函数的图像,探究对数函数的图像和性质. 1.数据分析、数学抽象、数学类比素养.
2.掌握对数函数的图象和性质. 2.逻辑推理素养
3.能利用对数函数的图像与性质来解决简单问题. 3.逻辑推理、数学建模素养.
温故知新
1.对数函数的概念
一般地,函数y = logax ,(a>0,且a≠1) 叫做对数函数,其中x是自变量,定义域是(0,+∞).
2.思考:
①指数函数y=ax(a>0,且a≠1)的定义域为 ,值域为 ;
②指数函数y=(a>0,且a≠1)的定义域为 ,值域为 .
③a0= (a>0,且a≠1),= (a>0,且a≠1).
R
R
(0,+∞)
(0,+∞)
1
0
温故知新
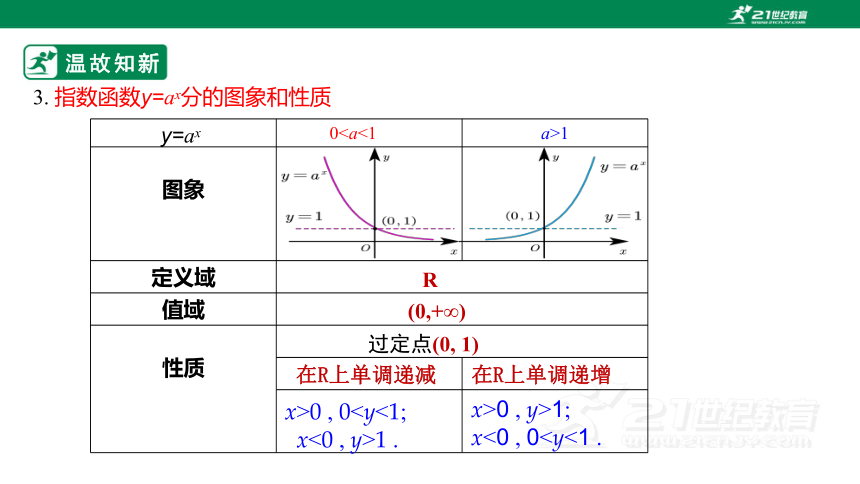
3. 指数函数y=ax分的图象和性质
图象
定义域 值域 性质
y=ax
0a>1
R
(0,+∞)
过定点(0, 1)
在R上单调递增
在R上单调递减
x>0 , 0x<0 , y>1 .
x>0 , y>1;
x<0 , 0新知探究
探究1.对数函数图象与性质
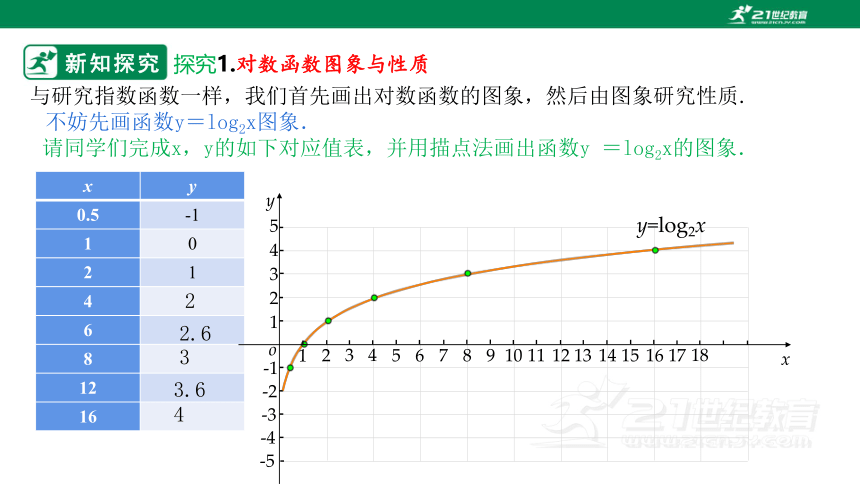
与研究指数函数一样,我们首先画出对数函数的图象,然后由图象研究性质.
x y
0.5 -1
1 0
2 1
4
6
8
12
16
2.6
2
3
3.6
4
作者:湛江市第五中学钟景荣
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
y=log2x
不妨先画函数y=log2x图象.
请同学们完成x,y的如下对应值表,并用描点法画出函数y =log2x的图象.
新知探究
探究1.对数函数图象与性质
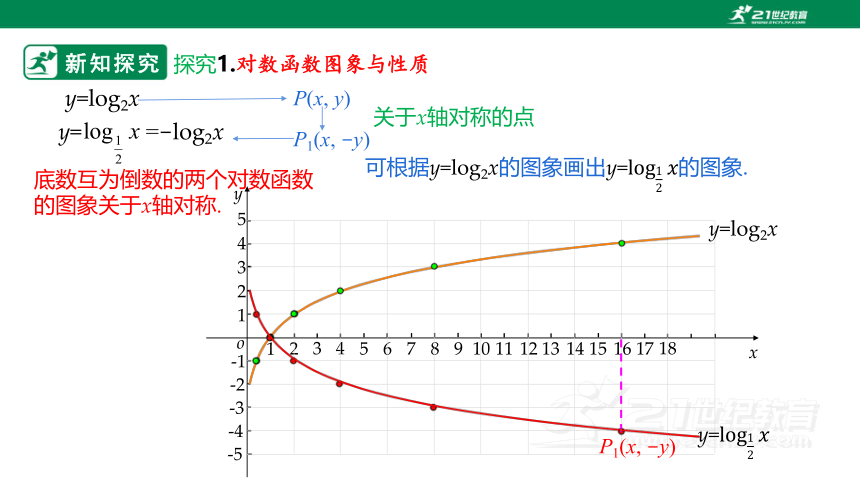
我们知道,底数互为倒数的两个指数函数的图象关于y轴对称,对于底数互为倒数的两个对数函数,比如y=log2x和 y=,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?
利用换底公式,可以得到y=.因为点(x,y)与点(x,-y)关于x轴对称,所以y=图象上任意一点P(x,y)关于x轴的对称点P1(x,-y)都在函数y= 的图象上,反之亦然.由此可知,底数互为倒数的两个对数函数的图象关于x轴对称.根据这种对称性,就可以利用y=的图象画出y=的图象.
新知探究
探究1.对数函数图象与性质
y=log2x
P(x, y)
y= =-log2x
P1(x, -y)
关于x轴对称的点
底数互为倒数的两个对数函数的图象关于x轴对称.
可根据y=log2x的图象画出y=的图象.
作者:湛江市第五中学钟景荣
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
P1(x, -y)
y=log2x
y=
新知探究
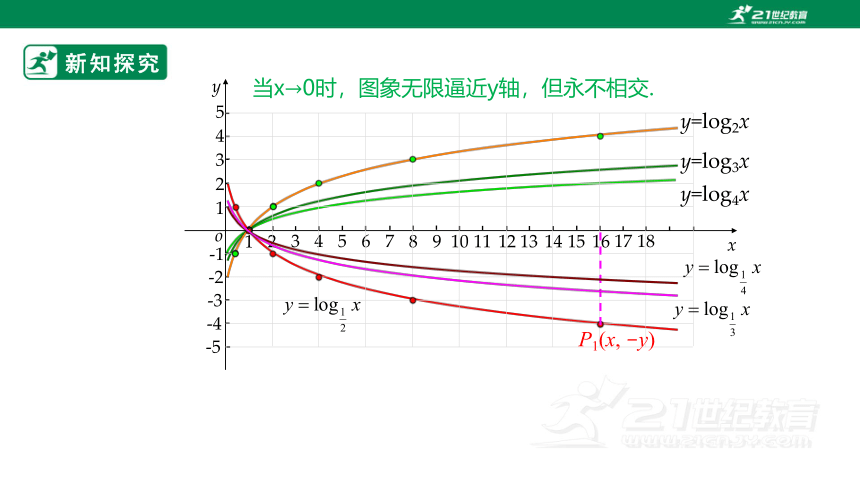
为了得到对数函数(a>0,且a≠1)的性质,我们还需要画出更多具体对数函数的图象进行观察.
选取底数a (a>0, 且a≠1)的若干个不同的值,例如a=3,a=4,a=, a=,在同一直角坐标系内画出相应的对数函数的图象,观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出对数函数y=logax (a>0,且a≠1)的值域和性质吗?对数函数是否也像指数函数一样,过某个定点?根据你所概括出的结论,自己设计一个表格,写出对数函数y=logax (a>0,且a≠1)的定义域、值域、单调性、奇偶性,等等.
新知探究
作者:湛江市第五中学钟景荣
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
P1(x, -y)
y=log2x
y=log3x
y=log4x
当x0时,图象无限逼近y轴,但永不相交.
新知探究
o
x
y
o
x
y
+∞
+∞
+∞
- ∞
+∞
- ∞
·
·
(1,0)
(1,0)
当x>1时,y>0;
当0当00;
当x>1时,y<0
y=logax(a>1)
y=logax(0新知探究
对数函数y=的图像与性质
01
图 像
定义域 值域 过定点 性质 单 调 性
取值分布
奇 偶 性 底数的变化对图像的影响: 底数互为倒数的两个对数函数图像的关系: (0,+∞)
R
(1,0)
在(0,+∞)上是增函数
既不是奇函数也不是偶函数
当x>1时y>0;当0当x>1时y<0;当00.
在(0,+∞)上是减函数
在直线x=1右侧,当a>1时,a越大图像越靠近x轴;当a<1时,a越小越靠近x轴
关于x轴对称
同正异负
新知讲解
【例1】函数f(x)=loga(x-2)-2x(a>0,且a≠1)的图像必经过定点 .
解:
令x-2=1,解得x = 3,
∴f (3)=loga(3-2)-2×3=-6,
即函数的 f (x)=loga(x-2)-2x的图象必经过定点(3,-6).
根据对数函数y=logax(a>0,且a≠1)的图象恒过定点(1,0),得到与对数函数所过的定点坐标.
新知讲解
【例2】比较下列各题中两个值的大小:
(1) log23.4 , log28.5 ; (2) log0.31.8 , log0.32.7 ;
(3) loga5.1 , loga5.9 (a>0 , 且a≠1) .
解:
(1)log23.4和log28.5可看作函数y=log2x的两个函数值.
因为底数2>1 ,对数函数y=log2x是增函数,且3.4<8.5,所以
log23.4 < log28.5 .
(2) log0.31.8和log0.32.7可看作函数y=log0.3x的两个函数值.
因为底数0<0.3<1 ,对数函数y=log0.3x是减函数, 且1.8<2.7, 所以
log0.31.8 > log0.32.7 .
新知讲解
【例2】比较下列各题中两个值的大小:
(1) log23.4 , log28.5 ; (2) log0.31.8 , log0.32.7 ;
(3) loga5.1 , loga5.9 (a>0 , 且a≠1) .
解:
(3) loga5.1 和 loga5.9可看作函数y=logax的两个函数值.
对数函数的单调性取决于底数a是大于1还是小于1,因此需要对底数a进行讨论.
①当a>1时,对数函数y=logax是增函数,且5.1<5.9,所以
loga5.1 < loga5.9.
②当0loga5.1 > loga5.9.
新知讲解
【例3】比较下列各题中两个值的大小:
(1) ; (2) .
解:
(1)可看作函数y=的一个函数值,可看作函数y=的一个函数值.
因为底数0<0.3<1,对数函数y=log0.3x是减函数;又因为3>1,对数函数y=是增函数.而1.8>1,2.7>1.
所以.
则.
(2)可看作函数y=的一个函数值,可看作函数y=的一个函数值.函数y=都是增函数.
因为7>6,所以.
则.
新知讲解
对数值比较大小的常用方法:
1.底数相同时:①先看底数判断单调性;
②后看真数比大小.
2.底数不同时:通常用1,0,-1作为中间量,对参与比较的数进行分类,再进行大小比较.(搭桥比较法)
初试身手
3解析:因为函数都是增函数,而,∴.故选C.
1.函数的f(x)=loga(x-2)(a>0,且a≠1)的图象必经过定点 .
2.比较下列各组中两个值的大小:
(1)log31.9 ,log32; (2)log23,log0.32.
3.a=log52,b=log83,c=,则下列判断正确的是( )
A.c<b<a B.b<a<c C.a<c<b D.a<b<c
>
>
(3,1)
C
新知探究
【例4】溶液酸碱度的测量.
溶液酸碱度是通过pH计量的.pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
解:
(1)根据对数的运算性质,有
,
在上,随着的增大, 减小,相应地,减小.
所以,随着的增大, 减小.即溶液中氢离子的浓度越大,溶液的酸性就越强.
新知探究
【例4】溶液酸碱度的测量.
溶液酸碱度是通过pH计量的.pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
解:
(2)当[H+]=10-7时,pH=-=7.
所以,纯净水的是.
初试身手
4.分贝是计量声音强度相对大小的单位。物理学家引入了声压级(spl)来描述声音的大小:把一很小的声压P0=2×10-5帕作为参考声压,把所要测量的声压P与参考声压P0的比值取常用对数后乘以20得到的数值成为声压级。声压级是听力学中最重要的参数之一,单位是分贝(dB)。分贝值在60以下为无害区,60~110为过渡区,110以上为有害区。
(1)根据上述材料,列出声压级y与声压P的函数关系式;
(2)某地声压P=0.002帕,试问该地位以上所说的什么区,声音环境是否优良?
解:(1)由已知得y=20(其中P0=2×10-5).
(2)当P=0.002时,y=20=20lg102=40(分贝)
所以此地为声压无害区,环境优良.
新知探究
像前面我们学习,指数函数y=,x∈[0,+∞)和对数函数y=,x∈(0,1]这样,根据运算性质可以由一个推导出另外一个,并且一个函数的定义域和值域分别是另外一个函数的值域和定义域的,我们就称它们互为反函数(inverse function).
探究2.反函数的概念
从定义上,互为反函数的两个函数的定义域与值域正好互换,运算变化过程正好互逆,这是一种对称性.
对于指数函数y=2x,你能利用指数与对数间的关系,得到与之对应的对数函数吗?它们的定义域、值域之间有什么关系?它们互为反函数吗?
新知探究
探究2.反函数的概念
O
x
y
一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换.
思考探究:对于函数y=,反过来,x是y的函数吗?
新知探究
探究2.反函数的概念
观察 在同一个坐标系中画出指数函数与对数函数的图象,观察它们有什么联系?
课堂小结
o
x
y
1
o
x
y
1
定义域:( 0,+∞);值域:R.
定义域:( 0,+∞);值域:R.
过定点(1,0)即x=1时,y=0.
过定点(1,0)即x=1时,y=0.
x∈(0,1)y<0 x∈(1,+∞)时,y>0
增函数.
减函数.
非奇非偶
非奇非偶
a > 1
0 x∈(0,1)y>0,x∈(1,+∞)时,y<0
课堂小结
根据运算性质可以由一个推导出另外一个,并且一个函数的定义域和值域分别是另外一个函数的值域和定义域的,我们就称它们互为反函数(inverse function).
反函数的概念
一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换.
作业布置
作业:p140-141. 习题4.4 2,4,5,7,8.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第4章 指数函数与对数函数
4.4 对数函数
4.4.2 对数函数的图象和性质(第一课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.通过用描点法画具体对数函数的图像,探究对数函数的图像和性质. 1.数据分析、数学抽象、数学类比素养.
2.掌握对数函数的图象和性质. 2.逻辑推理素养
3.能利用对数函数的图像与性质来解决简单问题. 3.逻辑推理、数学建模素养.
温故知新
1.对数函数的概念
一般地,函数y = logax ,(a>0,且a≠1) 叫做对数函数,其中x是自变量,定义域是(0,+∞).
2.思考:
①指数函数y=ax(a>0,且a≠1)的定义域为 ,值域为 ;
②指数函数y=(a>0,且a≠1)的定义域为 ,值域为 .
③a0= (a>0,且a≠1),= (a>0,且a≠1).
R
R
(0,+∞)
(0,+∞)
1
0
温故知新
3. 指数函数y=ax分的图象和性质
图象
定义域 值域 性质
y=ax
0
R
(0,+∞)
过定点(0, 1)
在R上单调递增
在R上单调递减
x>0 , 0
x>0 , y>1;
x<0 , 0
探究1.对数函数图象与性质
与研究指数函数一样,我们首先画出对数函数的图象,然后由图象研究性质.
x y
0.5 -1
1 0
2 1
4
6
8
12
16
2.6
2
3
3.6
4
作者:湛江市第五中学钟景荣
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
y=log2x
不妨先画函数y=log2x图象.
请同学们完成x,y的如下对应值表,并用描点法画出函数y =log2x的图象.
新知探究
探究1.对数函数图象与性质
我们知道,底数互为倒数的两个指数函数的图象关于y轴对称,对于底数互为倒数的两个对数函数,比如y=log2x和 y=,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?
利用换底公式,可以得到y=.因为点(x,y)与点(x,-y)关于x轴对称,所以y=图象上任意一点P(x,y)关于x轴的对称点P1(x,-y)都在函数y= 的图象上,反之亦然.由此可知,底数互为倒数的两个对数函数的图象关于x轴对称.根据这种对称性,就可以利用y=的图象画出y=的图象.
新知探究
探究1.对数函数图象与性质
y=log2x
P(x, y)
y= =-log2x
P1(x, -y)
关于x轴对称的点
底数互为倒数的两个对数函数的图象关于x轴对称.
可根据y=log2x的图象画出y=的图象.
作者:湛江市第五中学钟景荣
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
P1(x, -y)
y=log2x
y=
新知探究
为了得到对数函数(a>0,且a≠1)的性质,我们还需要画出更多具体对数函数的图象进行观察.
选取底数a (a>0, 且a≠1)的若干个不同的值,例如a=3,a=4,a=, a=,在同一直角坐标系内画出相应的对数函数的图象,观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出对数函数y=logax (a>0,且a≠1)的值域和性质吗?对数函数是否也像指数函数一样,过某个定点?根据你所概括出的结论,自己设计一个表格,写出对数函数y=logax (a>0,且a≠1)的定义域、值域、单调性、奇偶性,等等.
新知探究
作者:湛江市第五中学钟景荣
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
P1(x, -y)
y=log2x
y=log3x
y=log4x
当x0时,图象无限逼近y轴,但永不相交.
新知探究
o
x
y
o
x
y
+∞
+∞
+∞
- ∞
+∞
- ∞
·
·
(1,0)
(1,0)
当x>1时,y>0;
当0
当x>1时,y<0
y=logax(a>1)
y=logax(0
对数函数y=的图像与性质
0
图 像
定义域 值域 过定点 性质 单 调 性
取值分布
奇 偶 性 底数的变化对图像的影响: 底数互为倒数的两个对数函数图像的关系: (0,+∞)
R
(1,0)
在(0,+∞)上是增函数
既不是奇函数也不是偶函数
当x>1时y>0;当0
在(0,+∞)上是减函数
在直线x=1右侧,当a>1时,a越大图像越靠近x轴;当a<1时,a越小越靠近x轴
关于x轴对称
同正异负
新知讲解
【例1】函数f(x)=loga(x-2)-2x(a>0,且a≠1)的图像必经过定点 .
解:
令x-2=1,解得x = 3,
∴f (3)=loga(3-2)-2×3=-6,
即函数的 f (x)=loga(x-2)-2x的图象必经过定点(3,-6).
根据对数函数y=logax(a>0,且a≠1)的图象恒过定点(1,0),得到与对数函数所过的定点坐标.
新知讲解
【例2】比较下列各题中两个值的大小:
(1) log23.4 , log28.5 ; (2) log0.31.8 , log0.32.7 ;
(3) loga5.1 , loga5.9 (a>0 , 且a≠1) .
解:
(1)log23.4和log28.5可看作函数y=log2x的两个函数值.
因为底数2>1 ,对数函数y=log2x是增函数,且3.4<8.5,所以
log23.4 < log28.5 .
(2) log0.31.8和log0.32.7可看作函数y=log0.3x的两个函数值.
因为底数0<0.3<1 ,对数函数y=log0.3x是减函数, 且1.8<2.7, 所以
log0.31.8 > log0.32.7 .
新知讲解
【例2】比较下列各题中两个值的大小:
(1) log23.4 , log28.5 ; (2) log0.31.8 , log0.32.7 ;
(3) loga5.1 , loga5.9 (a>0 , 且a≠1) .
解:
(3) loga5.1 和 loga5.9可看作函数y=logax的两个函数值.
对数函数的单调性取决于底数a是大于1还是小于1,因此需要对底数a进行讨论.
①当a>1时,对数函数y=logax是增函数,且5.1<5.9,所以
loga5.1 < loga5.9.
②当0
新知讲解
【例3】比较下列各题中两个值的大小:
(1) ; (2) .
解:
(1)可看作函数y=的一个函数值,可看作函数y=的一个函数值.
因为底数0<0.3<1,对数函数y=log0.3x是减函数;又因为3>1,对数函数y=是增函数.而1.8>1,2.7>1.
所以.
则.
(2)可看作函数y=的一个函数值,可看作函数y=的一个函数值.函数y=都是增函数.
因为7>6,所以.
则.
新知讲解
对数值比较大小的常用方法:
1.底数相同时:①先看底数判断单调性;
②后看真数比大小.
2.底数不同时:通常用1,0,-1作为中间量,对参与比较的数进行分类,再进行大小比较.(搭桥比较法)
初试身手
3解析:因为函数都是增函数,而,∴.故选C.
1.函数的f(x)=loga(x-2)(a>0,且a≠1)的图象必经过定点 .
2.比较下列各组中两个值的大小:
(1)log31.9 ,log32; (2)log23,log0.32.
3.a=log52,b=log83,c=,则下列判断正确的是( )
A.c<b<a B.b<a<c C.a<c<b D.a<b<c
>
>
(3,1)
C
新知探究
【例4】溶液酸碱度的测量.
溶液酸碱度是通过pH计量的.pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
解:
(1)根据对数的运算性质,有
,
在上,随着的增大, 减小,相应地,减小.
所以,随着的增大, 减小.即溶液中氢离子的浓度越大,溶液的酸性就越强.
新知探究
【例4】溶液酸碱度的测量.
溶液酸碱度是通过pH计量的.pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
解:
(2)当[H+]=10-7时,pH=-=7.
所以,纯净水的是.
初试身手
4.分贝是计量声音强度相对大小的单位。物理学家引入了声压级(spl)来描述声音的大小:把一很小的声压P0=2×10-5帕作为参考声压,把所要测量的声压P与参考声压P0的比值取常用对数后乘以20得到的数值成为声压级。声压级是听力学中最重要的参数之一,单位是分贝(dB)。分贝值在60以下为无害区,60~110为过渡区,110以上为有害区。
(1)根据上述材料,列出声压级y与声压P的函数关系式;
(2)某地声压P=0.002帕,试问该地位以上所说的什么区,声音环境是否优良?
解:(1)由已知得y=20(其中P0=2×10-5).
(2)当P=0.002时,y=20=20lg102=40(分贝)
所以此地为声压无害区,环境优良.
新知探究
像前面我们学习,指数函数y=,x∈[0,+∞)和对数函数y=,x∈(0,1]这样,根据运算性质可以由一个推导出另外一个,并且一个函数的定义域和值域分别是另外一个函数的值域和定义域的,我们就称它们互为反函数(inverse function).
探究2.反函数的概念
从定义上,互为反函数的两个函数的定义域与值域正好互换,运算变化过程正好互逆,这是一种对称性.
对于指数函数y=2x,你能利用指数与对数间的关系,得到与之对应的对数函数吗?它们的定义域、值域之间有什么关系?它们互为反函数吗?
新知探究
探究2.反函数的概念
O
x
y
一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换.
思考探究:对于函数y=,反过来,x是y的函数吗?
新知探究
探究2.反函数的概念
观察 在同一个坐标系中画出指数函数与对数函数的图象,观察它们有什么联系?
课堂小结
o
x
y
1
o
x
y
1
定义域:( 0,+∞);值域:R.
定义域:( 0,+∞);值域:R.
过定点(1,0)即x=1时,y=0.
过定点(1,0)即x=1时,y=0.
x∈(0,1)y<0 x∈(1,+∞)时,y>0
增函数.
减函数.
非奇非偶
非奇非偶
a > 1
0 x∈(0,1)y>0,x∈(1,+∞)时,y<0
课堂小结
根据运算性质可以由一个推导出另外一个,并且一个函数的定义域和值域分别是另外一个函数的值域和定义域的,我们就称它们互为反函数(inverse function).
反函数的概念
一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换.
作业布置
作业:p140-141. 习题4.4 2,4,5,7,8.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
