6.3实数课件
图片预览





文档简介
课件25张PPT。
6.3 实数6.3 实数(1)了解无理数和实数的概念。
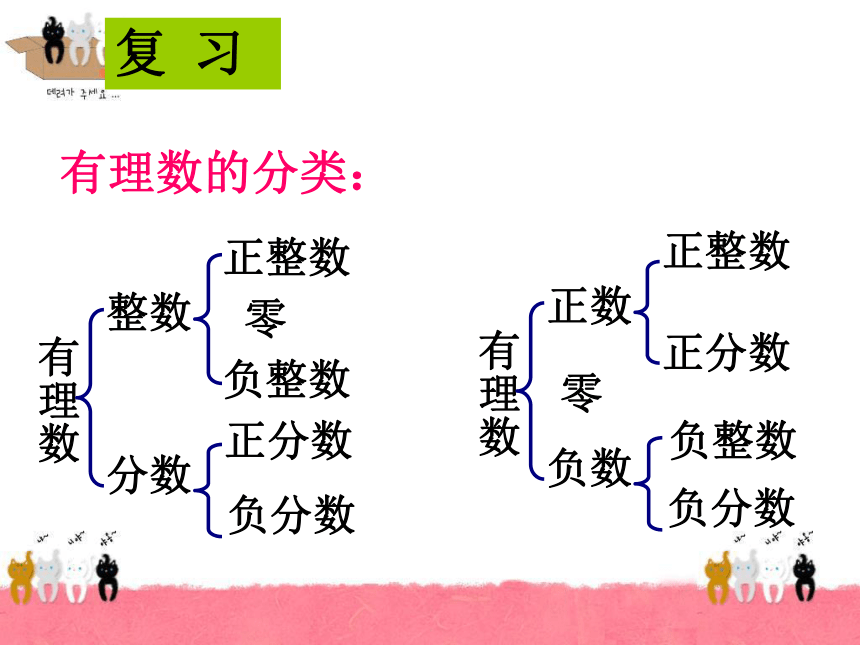
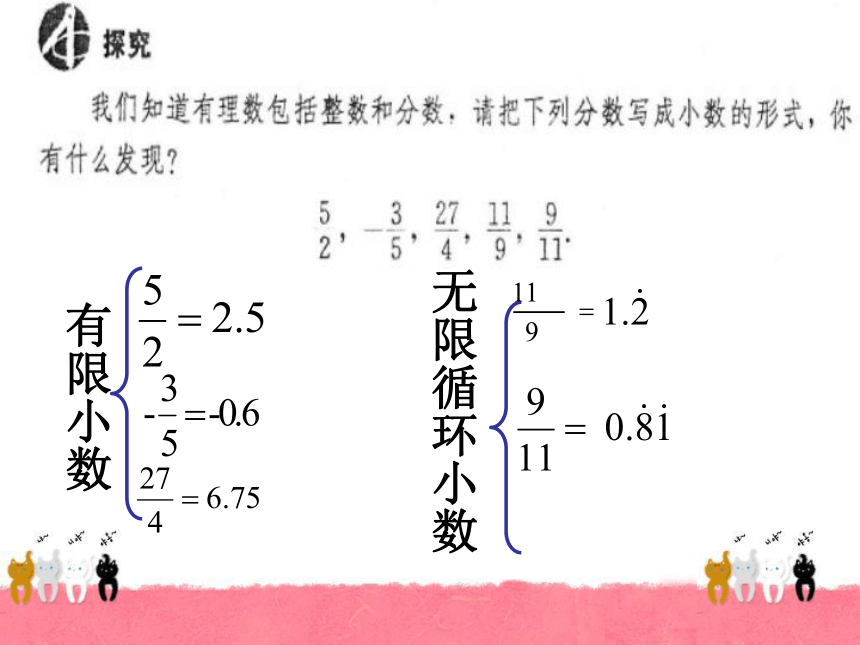
(2)知道实数与数轴上的点具有一一对应的关系,初步体会“数形结合”的数学思想。莒县小店镇中心初级中学 jvxianxiaodianzhenzhongxinchujizhongxue 学习目标复 习有理数的分类:有限小数无限循环小数 反过来,任何有限小数或无限循环小数也都是有理数除了有限小数和无限循环小数外,还有其它类型的小数吗? 无限不循环小数-------叫做无理数 事实上,任何一个有理数都可以写成有限小数或无限循环小数。有理数和无理数统称实数.2.开方开不尽的数。如3.有一定的规律,但
不循环的无限小数无理数的特征:(常见无理数的三种形式)注意:带根号的数不一定是无理数
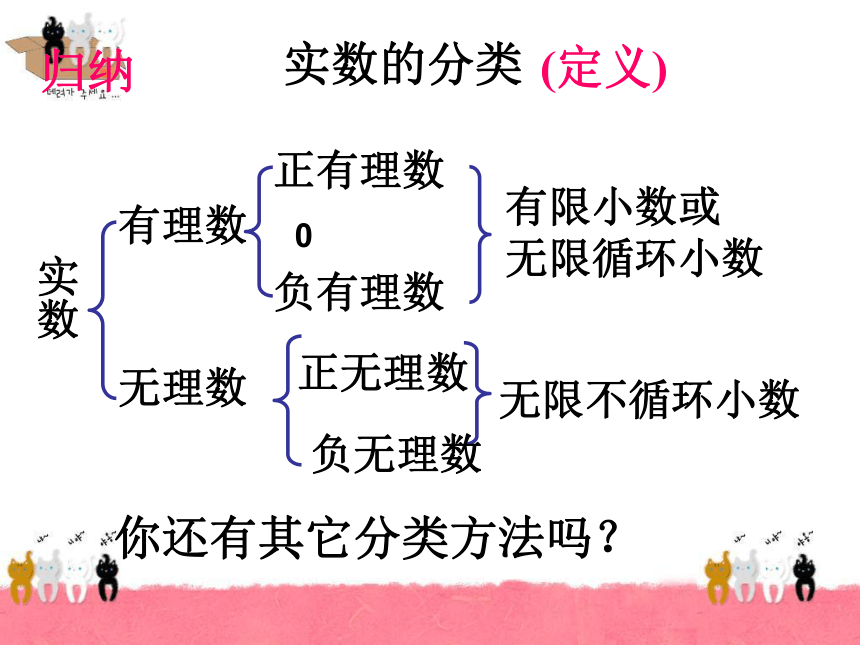
归纳实数的分类实数有理数无理数正有理数负有理数有限小数或
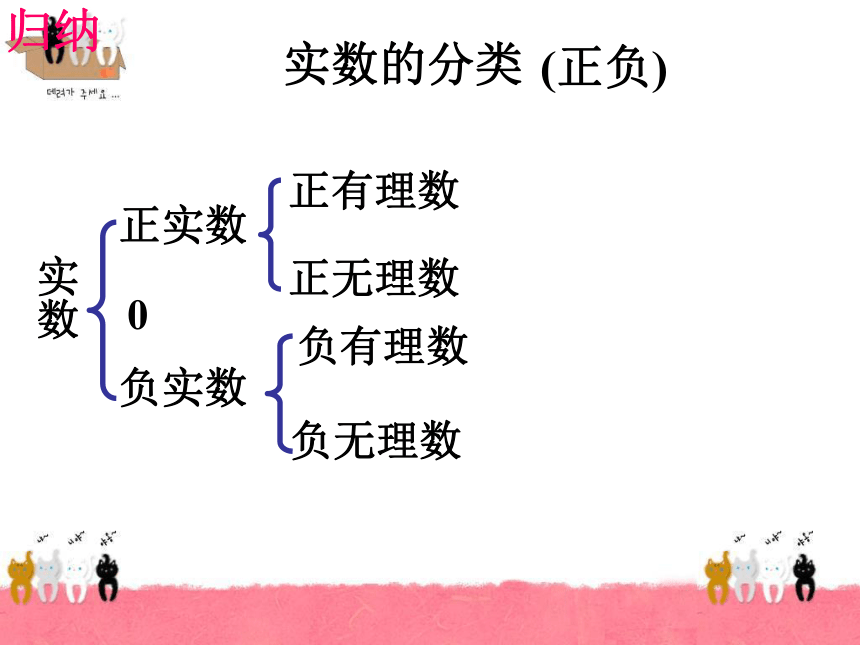
无限循环小数无限不循环小数你还有其它分类方法吗?(定义)0正无理数负无理数归纳实数的分类实数正实数负实数正有理数正无理数0负无理数负有理数(正负)导学案针对性练习和巩固性练习一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××8.有理数与无理数之和一定是无理数 ( )× 有理数集合 无理数集合 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A表示的数是多少?A有理数能在数轴上表示,那么无理数能在数轴上表示出来吗?无理数 、 可以用数轴上的点表示.探究2
事实上,任何一个无理数都可以用数轴上的点来表示。也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.实数与数轴上的点是一一对应的.结论探究的相反数是 ;的相反数是 ;的相反数是 ;-2 -1 0 1 2a的相反数是-a探究-2 -1 0 1 2正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.例题解析在进行实数运算时,有理数的运算法则及运算性质同样适用例2:计算下列各式的值练习π-3.14的相反数是_________3.14-π45、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数巩固 的值是( )
A B
C D
6.3 实数6.3 实数(1)了解无理数和实数的概念。
(2)知道实数与数轴上的点具有一一对应的关系,初步体会“数形结合”的数学思想。莒县小店镇中心初级中学 jvxianxiaodianzhenzhongxinchujizhongxue 学习目标复 习有理数的分类:有限小数无限循环小数 反过来,任何有限小数或无限循环小数也都是有理数除了有限小数和无限循环小数外,还有其它类型的小数吗? 无限不循环小数-------叫做无理数 事实上,任何一个有理数都可以写成有限小数或无限循环小数。有理数和无理数统称实数.2.开方开不尽的数。如3.有一定的规律,但
不循环的无限小数无理数的特征:(常见无理数的三种形式)注意:带根号的数不一定是无理数
归纳实数的分类实数有理数无理数正有理数负有理数有限小数或
无限循环小数无限不循环小数你还有其它分类方法吗?(定义)0正无理数负无理数归纳实数的分类实数正实数负实数正有理数正无理数0负无理数负有理数(正负)导学案针对性练习和巩固性练习一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××8.有理数与无理数之和一定是无理数 ( )× 有理数集合 无理数集合 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A表示的数是多少?A有理数能在数轴上表示,那么无理数能在数轴上表示出来吗?无理数 、 可以用数轴上的点表示.探究2
事实上,任何一个无理数都可以用数轴上的点来表示。也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.实数与数轴上的点是一一对应的.结论探究的相反数是 ;的相反数是 ;的相反数是 ;-2 -1 0 1 2a的相反数是-a探究-2 -1 0 1 2正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.例题解析在进行实数运算时,有理数的运算法则及运算性质同样适用例2:计算下列各式的值练习π-3.14的相反数是_________3.14-π45、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数巩固 的值是( )
A B
C D
