人教版八年级上册第十一章 三角形 单元检测试卷(含答案)
文档属性
| 名称 | 人教版八年级上册第十一章 三角形 单元检测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 362.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 00:00:00 | ||
图片预览

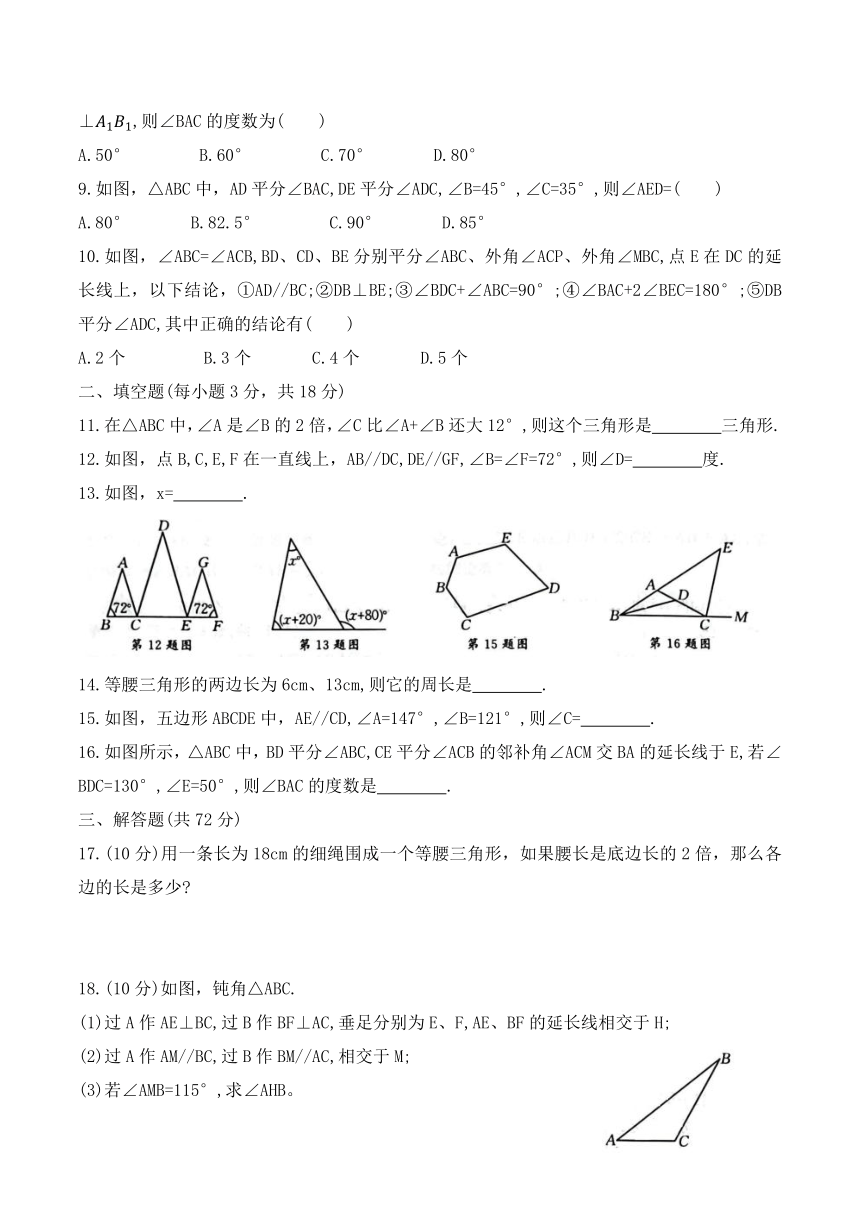
文档简介
《三角形》单元检测试卷
一、选择题(每小题3分,共30分)
1.现有两根木棒,它们的长分别是20cm和30cm,若不改变木棒的长短,要钉成一个三角形木架,则应在下列四根木棒中选取( )
A.10cm的木棒 B.20cm的术林 C.50cm的木林 D.60cm的木棒
2.在三角形的三个外角(一个顶点只取一个外角)中,钝角的个数至少是( )
A.3 B.2 C.1 D.0
3.如图,工人师傅砌门时,常用木条EF固定短形门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短 B.矩形的对称性
C.矩形的四个角都是直角 D.三角形的稳定性
4.画△ABC中AB边上的高,下列画法正确的是( )
5.如图,CD//AB,∠1=120°,∠2=80°,则∠E的度数是( )
A.40° B.60° C.80° D.120°
6.若一个多边形的内角和与外角和之和是1800°,则此多边形是( )边形.
A.八 B.十 C.十二 D.十四
7.在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )
A.18.如图,将△ABC绕C点顺时针方向旋转20°,使B点落在B 位置,A点落在A 位置,使AC⊥,则∠BAC的度数为( )
A.50° B.60° C.70° D.80°
9.如图,△ABC中,AD平分∠BAC,DE平分∠ADC,∠B=45°,∠C=35°,则∠AED=( )
A.80° B.82.5° C.90° D.85°
10.如图,∠ABC=∠ACB,BD、CD、BE分别平分∠ABC、外角∠ACP、外角∠MBC,点E在DC的延长线上,以下结论,①AD//BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠BAC+2∠BEC=180°;⑤DB平分∠ADC,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共18分)
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 三角形.
12.如图,点B,C,E,F在一直线上,AB//DC,DE//GF,∠B=∠F=72°,则∠D= 度.
13.如图,x= .
14.等腰三角形的两边长为6cm、13cm,则它的周长是 .
15.如图,五边形ABCDE中,AE//CD,∠A=147°,∠B=121°,则∠C= .
16.如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM交BA的延长线于E,若∠BDC=130°,∠E=50°,则∠BAC的度数是 .
三、解答题(共72分)
17.(10分)用一条长为18cm的细绳围成一个等腰三角形,如果腰长是底边长的2倍,那么各边的长是多少
18.(10分)如图,钝角△ABC.
(1)过A作AE⊥BC,过B作BF⊥AC,垂足分别为E、F,AE、BF的延长线相交于H;
(2)过A作AM//BC,过B作BM//AC,相交于M;
(3)若∠AMB=115°,求∠AHB。
19.(10分)已知:∠B=∠C=∠BAD,∠ADC=∠DAC,AE⊥BC,求∠DAE.
20.(10分)如图,已知AD//BC,AE、BE分别平分∠DAB、∠CBA,过E作FG分别交AD、BC于F、
G,∠AEF=28°,求∠BEG的大小.
21.(10分)如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:
(1)若∠A=50°,求∠BOC的度数;
(2)在其他条件不变的情况下,∠A与∠BOC之间有怎样的数量关系
22.(10分)已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
23.(12分)小明在学习三角形的知识时,发现如下三个有趣的结论;
在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,E为垂足,∠AME的平分线交直线AB于点F.
(1)如图1,M为边AC上一点,则BD、MF的位置关系是 ,并证明;
(2)如图2,M为边AC反向延长线上一点,则BD、MF的位置关系是 ,并证明;
(3)如图3,M为边AC延长线上一点,则BD、MF的位置关系是 ,并证明.
参考答案
1-5.BBDCA 6-10.BDCBC
11.钝角 12.36° 13.60° 14.32cm 15.92°16.120°
17.设底边长为x cm,则腰长为2x cm.
x+2x+2x=18,解得x=3.6.
答:三边长分别为3.6cm,7.2cm,7,2cm.
(1)略(2)略(3)65°
19.18°
20.62°
21.(1)∵∠A=50°,∴∠ABC+∠ACB=180°-∠A=130°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
(2)∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,∠OBC+∠OCB= (∠ABC+∠ACB),在△OBC中,
∠BOC=180°-(∠OBC+∠OCB)=180- (∠ABC+∠ACB)=180°- (180°-∠A)=90°+ ∠A,
即∠BOC=90+ ∠A.
22.(1)∠P=∠Q;(2)∠P+∠Q=180°.
23.(1)BD//MF;(2)BD⊥MF;(3)BD⊥MF,证略.
一、选择题(每小题3分,共30分)
1.现有两根木棒,它们的长分别是20cm和30cm,若不改变木棒的长短,要钉成一个三角形木架,则应在下列四根木棒中选取( )
A.10cm的木棒 B.20cm的术林 C.50cm的木林 D.60cm的木棒
2.在三角形的三个外角(一个顶点只取一个外角)中,钝角的个数至少是( )
A.3 B.2 C.1 D.0
3.如图,工人师傅砌门时,常用木条EF固定短形门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短 B.矩形的对称性
C.矩形的四个角都是直角 D.三角形的稳定性
4.画△ABC中AB边上的高,下列画法正确的是( )
5.如图,CD//AB,∠1=120°,∠2=80°,则∠E的度数是( )
A.40° B.60° C.80° D.120°
6.若一个多边形的内角和与外角和之和是1800°,则此多边形是( )边形.
A.八 B.十 C.十二 D.十四
7.在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )
A.1
A.50° B.60° C.70° D.80°
9.如图,△ABC中,AD平分∠BAC,DE平分∠ADC,∠B=45°,∠C=35°,则∠AED=( )
A.80° B.82.5° C.90° D.85°
10.如图,∠ABC=∠ACB,BD、CD、BE分别平分∠ABC、外角∠ACP、外角∠MBC,点E在DC的延长线上,以下结论,①AD//BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠BAC+2∠BEC=180°;⑤DB平分∠ADC,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共18分)
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 三角形.
12.如图,点B,C,E,F在一直线上,AB//DC,DE//GF,∠B=∠F=72°,则∠D= 度.
13.如图,x= .
14.等腰三角形的两边长为6cm、13cm,则它的周长是 .
15.如图,五边形ABCDE中,AE//CD,∠A=147°,∠B=121°,则∠C= .
16.如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM交BA的延长线于E,若∠BDC=130°,∠E=50°,则∠BAC的度数是 .
三、解答题(共72分)
17.(10分)用一条长为18cm的细绳围成一个等腰三角形,如果腰长是底边长的2倍,那么各边的长是多少
18.(10分)如图,钝角△ABC.
(1)过A作AE⊥BC,过B作BF⊥AC,垂足分别为E、F,AE、BF的延长线相交于H;
(2)过A作AM//BC,过B作BM//AC,相交于M;
(3)若∠AMB=115°,求∠AHB。
19.(10分)已知:∠B=∠C=∠BAD,∠ADC=∠DAC,AE⊥BC,求∠DAE.
20.(10分)如图,已知AD//BC,AE、BE分别平分∠DAB、∠CBA,过E作FG分别交AD、BC于F、
G,∠AEF=28°,求∠BEG的大小.
21.(10分)如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:
(1)若∠A=50°,求∠BOC的度数;
(2)在其他条件不变的情况下,∠A与∠BOC之间有怎样的数量关系
22.(10分)已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
23.(12分)小明在学习三角形的知识时,发现如下三个有趣的结论;
在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,E为垂足,∠AME的平分线交直线AB于点F.
(1)如图1,M为边AC上一点,则BD、MF的位置关系是 ,并证明;
(2)如图2,M为边AC反向延长线上一点,则BD、MF的位置关系是 ,并证明;
(3)如图3,M为边AC延长线上一点,则BD、MF的位置关系是 ,并证明.
参考答案
1-5.BBDCA 6-10.BDCBC
11.钝角 12.36° 13.60° 14.32cm 15.92°16.120°
17.设底边长为x cm,则腰长为2x cm.
x+2x+2x=18,解得x=3.6.
答:三边长分别为3.6cm,7.2cm,7,2cm.
(1)略(2)略(3)65°
19.18°
20.62°
21.(1)∵∠A=50°,∴∠ABC+∠ACB=180°-∠A=130°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
(2)∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,∠OBC+∠OCB= (∠ABC+∠ACB),在△OBC中,
∠BOC=180°-(∠OBC+∠OCB)=180- (∠ABC+∠ACB)=180°- (180°-∠A)=90°+ ∠A,
即∠BOC=90+ ∠A.
22.(1)∠P=∠Q;(2)∠P+∠Q=180°.
23.(1)BD//MF;(2)BD⊥MF;(3)BD⊥MF,证略.
