8.4对顶角 课件

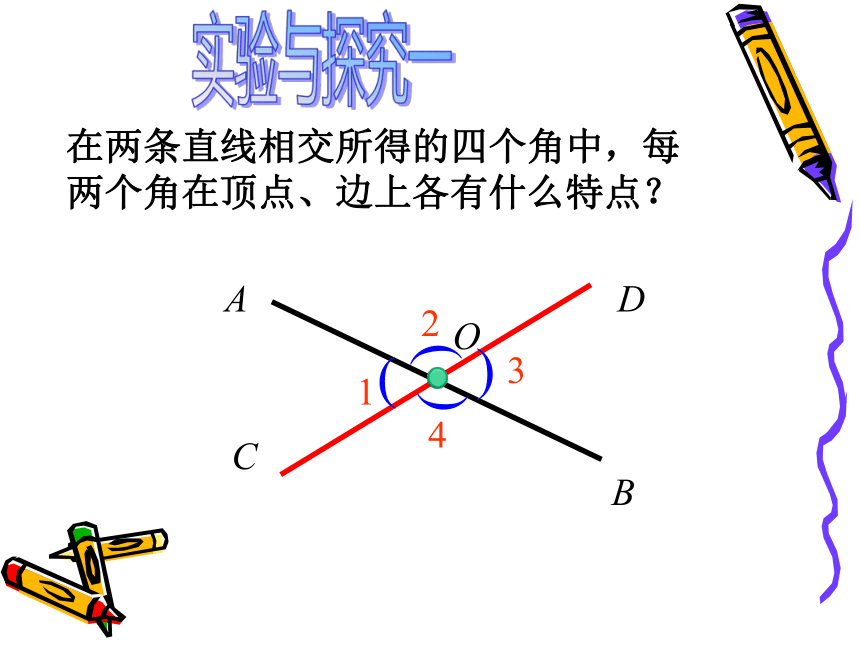
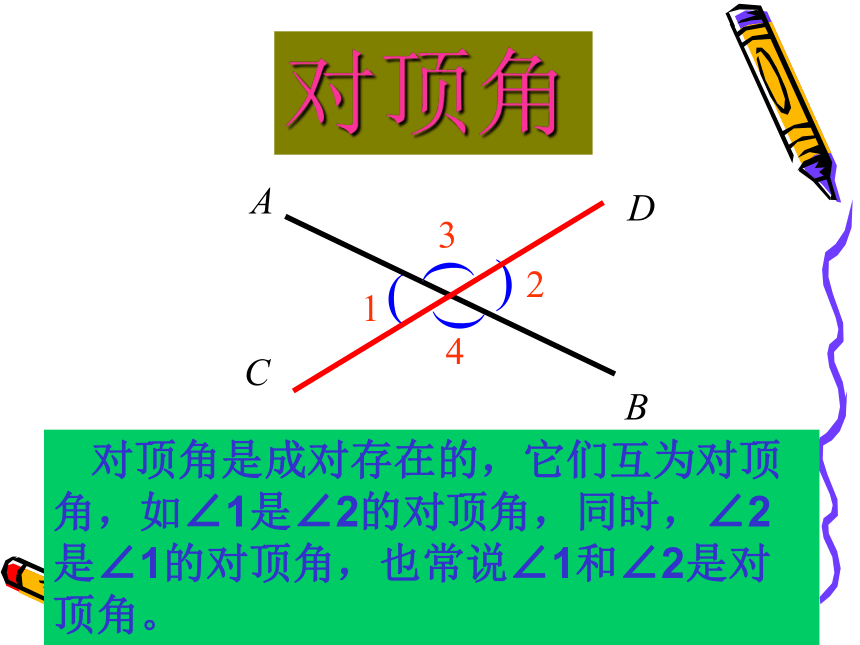
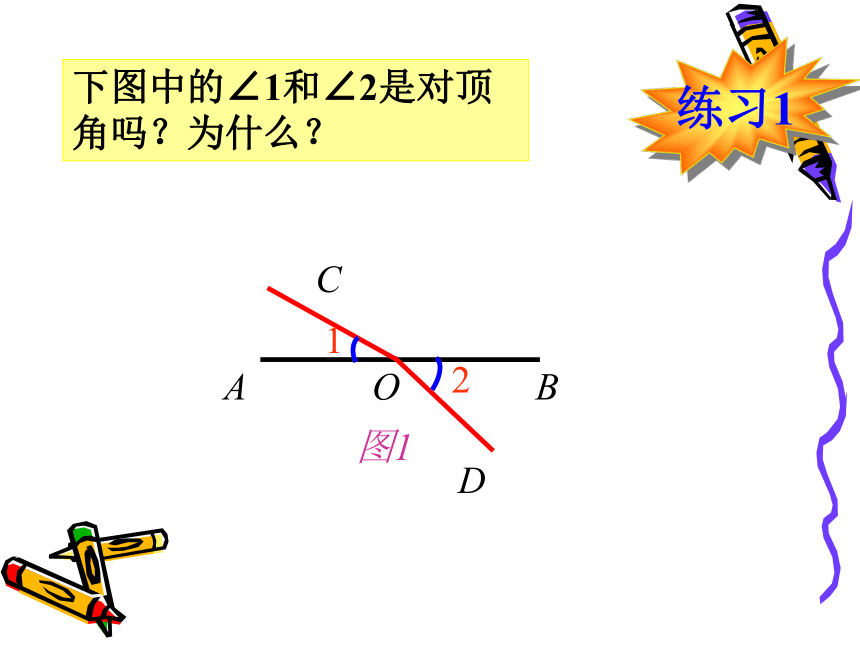
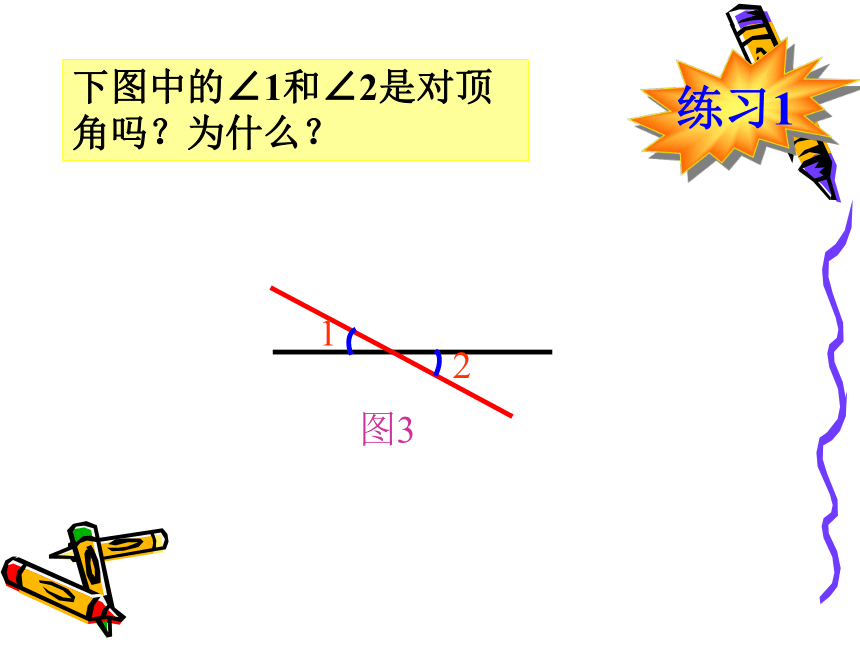
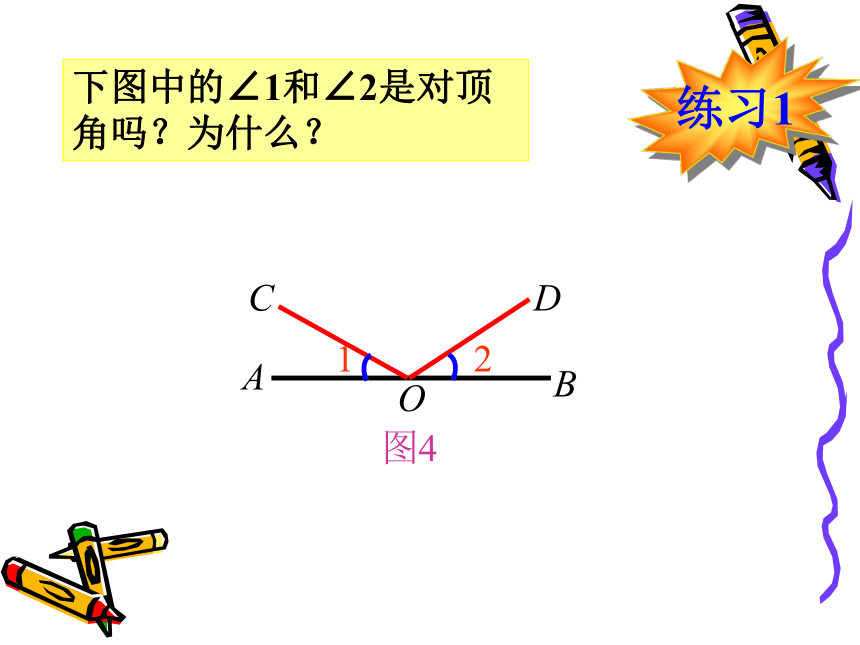
课件21张PPT。§8.4 对顶角第八章：角北京菜户营立交桥实验与探究一在两条直线相交所得的四个角中，每两个角在顶点、边上各有什么特点？OABCD　对顶角是成对存在的，它们互为对顶角，如∠1是∠2的对顶角，同时，∠2是∠1的对顶角，也常说∠1和∠2是对顶角。对顶角1图3对顶角满足的条件:一、两条直线相交所成的角；
二、有公共顶点；
三、两边互为反向延长线。
符合这三个条件时，才能确定这两个角是
对顶角，缺一个条件都不行.试一试BOA动动脑、动动手：
你能画出∠AOB的对顶角吗？))BDE如图，直线AB、CD、EF相交于点O，
∠AOD的对顶角是　　　　　，
∠BOE 的对顶角是　　　　　.
∠BOC∠AOFO练习2ACF实验与探究二在两条直线相交所得的四个角中，对顶角的大小存在怎样的关系。O交流与发现对顶角的性质判断正误：(1)如果两个角是对顶角，那么这两个角相等. (2)如果两个角不是对顶角，那么这两个角不相等. （对）（错）试一试：(3)如果两个角相等,那么这两个角是对顶角。 （错）(4)如果两个角不相等,那么这两个角不是对顶角。 （对）如图，直线AB和CD相交于点O,射线OE是∠BOD的角平分线，已知∠AOD=110°,求∠COB，∠AOC，∠BOE，∠EOD的度数。 例题ABCDO练习3 如图，要测量两墙围墙所形成的∠AOB的度数，
人站在墙外，不能进入，可以怎样测量？ 活动探究方法一:延长AO（或BO）到
点C，先测量出它的补角
∠BOC（或∠AOC）的度数 方法二：分别延长AO、BO，
测量出它的对顶角的度数 课堂小结学习目标：
1、了解对顶角的位置关系，
2、经历在数学活动中探索对顶角性质的过程，培养有
条理地思考与表达能力。
3、会应用对顶角的性质解决简单的角的计算问题。
交流一下这节课的学习目标你达到了吗？
哪里是你的难点？
当堂达标：
2.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
3.如图，AB、CD相交于点O，∠DOE= 90° ，∠AOC= 72° 。求∠BOE的度数。
再见