苏教版版数学六年级下册第一单元《扇形统计图》单元测试卷(基础卷)(含解析)
文档属性
| 名称 | 苏教版版数学六年级下册第一单元《扇形统计图》单元测试卷(基础卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 365.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 21:17:48 | ||
图片预览



文档简介
苏教版版数学六年级下册第一单元《扇形统计图》单元测试卷(基础卷)
【分层训练】苏教版六年级下册数学第一单元《扇形统计图》基础卷
一、单选题。(共6题;共12分)
1.人离不开水,成年人每天体内47%的水靠喝水获得,39%来自食物含的水,14%来自体内氧化时释放出来的水。最适合选用( )统计图来处理该数据。
A.条形 B.折线 C.扇形
2.医院要反映出一个病人一天的体温变化情况,最好用( )。
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上都可以
3.( )不仅能看出各种数量的多少,而且能呈现数量的增减变化情况。
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
4.开学初,要在六(1)班的48名学生中选出一名同学任班长。民主选举的结果如下表。
姓名 赵小铭 张红 何云飞 李晓勇
票数 24票 12票 7票 5票
如果将这一结果用扇形统计图表示,那么正确表示这一选举结果的是( )。
A. B. C. D.
5.某酒精溶液是由75%的水和25%的酒精形成的.下面图( )能正确地表示这个信息.
A. B. C. D.
6.要反映200毫升牛奶中钙、铁、锌等各种营养成分的含量多少,用( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.复式折线统计图
二、判断题。(共3题;共6分)
7.扇形统计图能清楚地看出数量的多少和数量变化的情况。 ( )
8.医生统计病人体温变化情况,较合适的是选择折线统计图。( )
9.扇形统计图的特点是只能比较清楚地看出各部分量的多少。( )
三、填空题。(共7题;共27分)
10.医生每四个小时给病人测温度变化选用( )统计图,统计住院各科人数时,选用( )
11.( )统计图可以清楚地表示出各部分数量与总数量之间的关系。要表示数量增减变化情况,用( )统计图比较合适。
12.某果园种苹果树面积占总面积的58%,种桔树面积占32%,余下的种桃树,若要制成扇形统计图,其中表示种桃树的面积的扇形圆心角是 度。
13.下图是某学校六年级学生喜欢球类运动的统计图:
(1)喜欢 和 的学生差不多。
(2)有200名学生参加了调查,喜欢足球运动的有 人。
(3)喜欢其他运动的同学占 %。
14.通过学习《科学》,我们知道我国国土面积约960万平方千米,下图是各种地形所占百分比情况.
(1)我国的平原面积是 万平方千米.
(2)我国的盆地面积比山地面积少 平方千米.
15.六年级有50人,每人只能参加一项课外活动,课外活动情况如下图所示。
(1)喜欢打 的人数最多,是 人。
(2)喜欢打 的人数最少,是 人。
(3)喜欢打篮球的有10人,占全班人数的 %。
16.如图是某校六年级(1)班学生为玉树灾区捐款情况抽样调查的条形统计图和扇形统计图。由图可知,六(1)班共有 人;在扇形统计图中,六(1)班捐款15元的人数所占的圆心角度数n的值为 ;若该校六年级学生有800人,据此信息可估计该校六年级捐款总数为 元。
四、解答题。(共6题;共55分)
17.一块蔬菜地中,种着青椒、黄瓜、丝瓜和茄子四种蔬菜.下图表示各种蔬菜的种植面积.
(1)青椒的种植面积占 %.
(2)如果丝瓜种植面积是300平方米,这块蔬菜地的总面积是 平方米.
(3) 的种植面积最大,比茄子面积多 %.
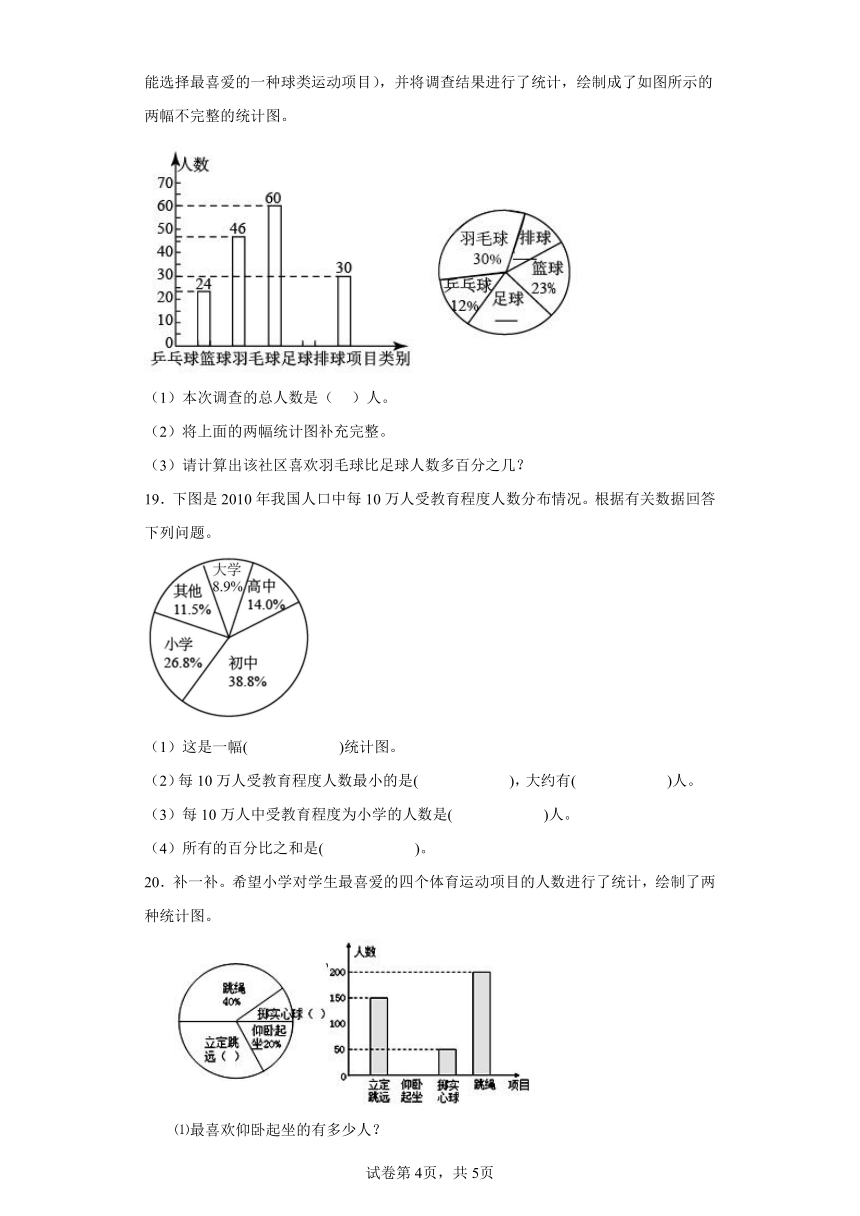
18.某社区为了解居民对足球、篮球、排球、羽毛球和乒乓球这五种球类运动项目的喜爱情况,在社区开展了“我最喜爱的球类运动项目”的随机调查(每位被调查者必须且只能选择最喜爱的一种球类运动项目),并将调查结果进行了统计,绘制成了如图所示的两幅不完整的统计图。
(1)本次调查的总人数是( )人。
(2)将上面的两幅统计图补充完整。
(3)请计算出该社区喜欢羽毛球比足球人数多百分之几?
19.下图是2010年我国人口中每10万人受教育程度人数分布情况。根据有关数据回答下列问题。
(1)这是一幅( )统计图。
(2)每10万人受教育程度人数最小的是( ),大约有( )人。
(3)每10万人中受教育程度为小学的人数是( )人。
(4)所有的百分比之和是( )。
20.补一补。希望小学对学生最喜爱的四个体育运动项目的人数进行了统计,绘制了两种统计图。
⑴最喜欢仰卧起坐的有多少人?
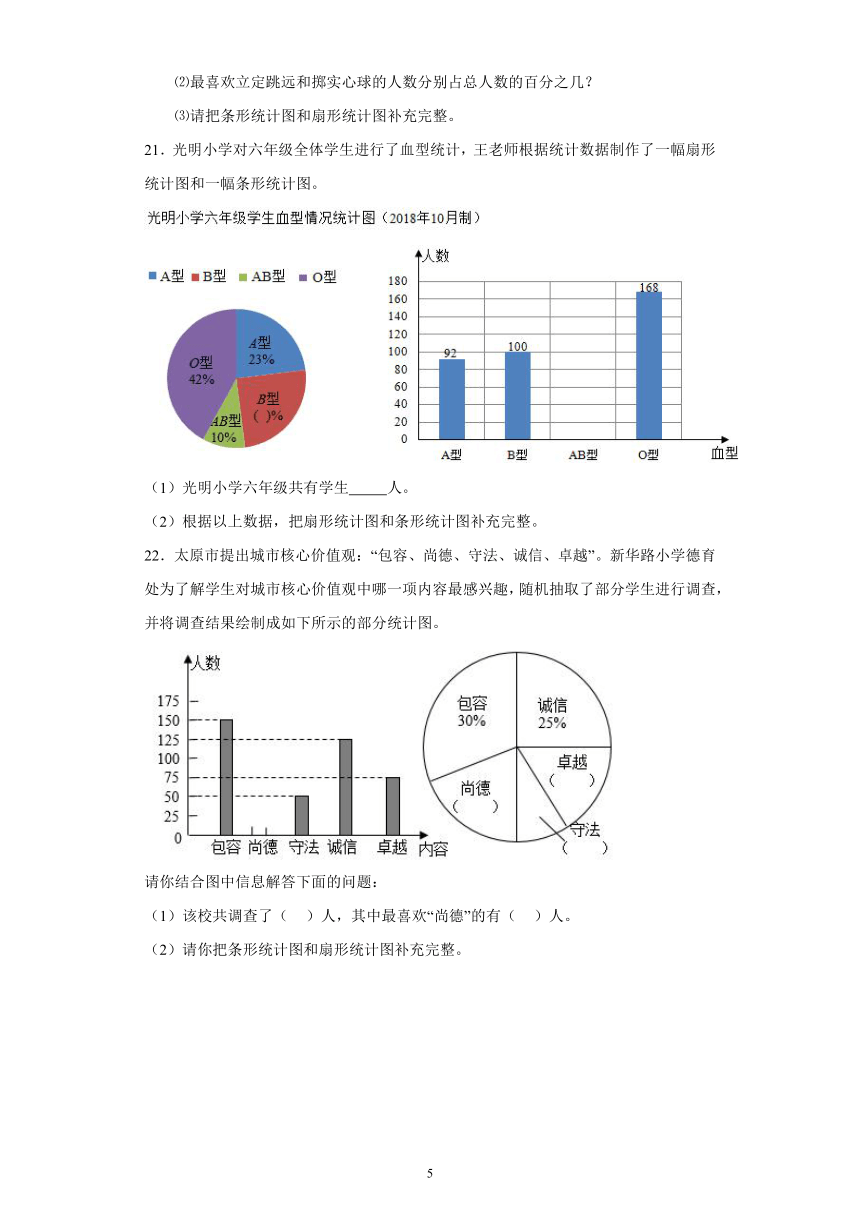
⑵最喜欢立定跳远和掷实心球的人数分别占总人数的百分之几?
⑶请把条形统计图和扇形统计图补充完整。
21.光明小学对六年级全体学生进行了血型统计,王老师根据统计数据制作了一幅扇形统计图和一幅条形统计图。
(1)光明小学六年级共有学生 人。
(2)根据以上数据,把扇形统计图和条形统计图补充完整。
22.太原市提出城市核心价值观:“包容、尚德、守法、诚信、卓越”。新华路小学德育处为了解学生对城市核心价值观中哪一项内容最感兴趣,随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的部分统计图。
请你结合图中信息解答下面的问题:
(1)该校共调查了( )人,其中最喜欢“尚德”的有( )人。
(2)请你把条形统计图和扇形统计图补充完整。
参考答案:
1.C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此解答即可。
【详解】根据统计图的特点可知,成年人每天体内47%的水靠喝水获得,39%来自食物含的水,14%来自体内氧化时释放出来的水,用扇形统计图表示比较合适。
故答案为:C
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
2.B
【分析】折线统计图能清楚的看出数量的增减变化情况,所以观察病人的体温变化情况,最好用折线统计图。
【详解】医院要反映出一个病人一天的体温变化情况,最好用折线统计图。
故答案为:B。
【点睛】此题考查根据实际情况选择统计图,需熟练掌握各种统计图的特点。
3.B
【分析】折线统计图用折线的起伏表示数据的增减变化情况。不仅可以表示数量的多少,而且可以反映数据的增减变化情况。
条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。从条形统计图中很容易看出各种数量的多少。
扇形统计图是用整个圆表示总数(单位“1”),用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几,扇形统计图中各部分的百分比之和是单位“1”。
统计表可以更加清晰、明了地反映数据的情况。
据此选择。
【详解】折线统计图不仅能看出各种数量的多少,而且能呈现数量的增减变化情况。
故答案为:B。
【点睛】此题考查统计图表的选择,掌握各种统计图的特点是解题关键。
4.A
【分析】扇形统计图是用整个圆表示总数单位“1”,用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几,扇形统计图中各部分的百分比之和是单位“1”。本题中把六(1)班总人数(48)人看作单位“1”,根据求一个数是另一个数的百分之几,分别求出四名同学的得票率,然后与4幅统计图进行比较即可。
【详解】赵小铭:24÷48=0.5=50%,即赵小铭的票数是全班同学的50%,即占圆的一半。也就是;
张红:12÷48=0.25=25%,张红的票数是全班同学的25%,即占圆的;
何云飞+李小勇:(7+5)÷48=0.25=25%,两人共占全班人数的25%,即占圆;
首先排除图C、图D,因为这两幅图中都没有表示50%的扇形;图B也没有表示25%的扇形,所以只有图A符合题意。
故答案选:A
【点睛】本题考查扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
5.D
【详解】360°×25%=90°,表示酒精的扇形的圆心角是90°,所以D图正确。
故答案为:D
【点睛】用360°乘酒精占的百分率即可求出表示酒精的扇形的圆心角的度数,然后选择图形即可。
6.C
【分析】扇形统计图能反映部分与整体的关系,据此作答即可。
【详解】反映200毫升牛奶中钙、铁、锌等各种营养成分的含量多少,用扇形统计图比较合适。
故答案为:C。
【点睛】此题考查统计图的选择,掌握各种统计图的特点是解题关键。
7.×
【分析】条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。据此判断。
【详解】折线统计图能清楚地看出数量的多少和数量变化的情况。原题说法错误。
故答案为:×。
【点睛】熟练掌握各种统计图的特点是解题关键。
8.√
【分析】折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况,据此解答。
【详解】医生统计病人体温变化情况,较合适的是选择折线统计图。
故答案为:√
【点睛】掌握折线统计图的特点是解答此题的关键。
9.×
【分析】扇形统计图描述的是各部分所占的百分比,条形统计图描述的是各部分具体的数量。
【详解】扇形统计图的特点是只能清楚地看出各部分所占的百分比。
故原说法错误。
【点睛】本题考查扇形统计图的特征,熟记各类统计图的特征是解答此题的关键。
10. 折线 条形统计图
【详解】略
11. 扇形 折线
【分析】三种统计图特点:条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势;扇形统计图可以显示部分与总体的关系。
【详解】扇形统计图可以清楚地表示出各部分数量与总数量之间的关系。要表示数量增减变化情况,用折线统计图比较合适。
【点睛】熟练掌握各种统计图的特点是解题关键。
12.36
【详解】略
13. 排球 篮球 50 13
【分析】(1)根据每种球喜欢的人数占总人数的百分率判断喜欢哪两种运动的人数差不多;
(2)用参加调查的人数乘喜欢足球运动的百分率即可求出喜欢足球运动的人数;
(3)用1减去已知的4种运动的百分率即可求出喜欢其他运动的同学占总人数的百分率。
【详解】(1)18%和19%差不多,所以喜欢排球和篮球的学生差不多;
(2)200×25%=50(人)
(3)1-(25%+18%+25%+19%)
=1-87%
=13%
14. 115.2 134.4
【详解】略
15. 乒乓球 20 羽毛球 5 20
【分析】根据扇形统计图,占的区域面积最大,则人数最多,占的面积最小,则人数最少,之后用总人数分别乘对应的百分率即可求出对应的人数;喜欢打篮球的人数占全班人数的百分之多少,用喜欢打篮球的人数÷全班人数×100%,把数代入即可求解。
【详解】(1)50×40%=20(人)
喜欢打乒乓球的人数最多,是20人。
(2)50×10%=5(人)
喜欢打羽毛球的人数最少,是5人。
(3)10÷50×100%
=0.2×100%
=20%
【点睛】本题关键是根据扇形统计图的特点,找出单位“1”,进一步理清解答思路,列式的顺序,从而较好的解答问题。
16. 50 72° 7600
【分析】(1)根据由条形统计图提供的数据,求出各捐款数的人数之和就是该班总人数。
(2)捐款15元的人数占总人数的几分之几,扇形的圆心角就是360°的几分之几。
(3)先求出六(1)班平均每人捐款数再乘800即可估计六年级捐款总数。
【详解】(1)六(1)班共有:15+25+10=50(人)
(2)六(1)班捐款15元的人数所占的圆心角度数n的值为:360°×=72°
(3)据此信息可估计该校六年级捐款总数为:
(5×15+10×25+15×10)÷(15+25+10)
=720÷50
=9.5(元)
9.5×800=7600(元)
17. 20 1200 黄瓜 350
【分析】(1)根据题意,将这块蔬菜的总面积看作单位“1”,青椒地的种植面积可用单位“1”分别减去丝瓜、黄瓜、茄子各占总面积的百分数即可;(2)可用丝瓜的面积300平方米除以丝瓜占总面积的25%即可得到蔬菜的总面积,列式解答即可得到答案;(3)根据图示,黄瓜的种植面积最大,可用总的蔬菜地的面积分别乘黄瓜、茄子各占总面积的百分数即可得到黄瓜、茄子的种植面积,再用黄瓜的种植面积减去茄子的种植面积除以茄子的面积乘100%即可.
【详解】(1)1﹣25%﹣10%﹣45%=75%﹣10%﹣45%=65%﹣45%=20%;
故填:20%;
(2)300÷25%=1200(平方米);
故填:1200;
(3)黄瓜的种植面积为:1200×45%=540(平方米),
茄子的种植面积为:1200×10%=120(平方米),
(540﹣120)÷120,=420÷120=3.5=350%;
故填:黄瓜,350%.
故答案为(1)20%,(2)1200,(3)黄瓜,350%.
18.(1)200
(2)
(3)50%
【分析】(1)观察条形统计图可知,喜欢羽毛球的人数有60人,观察扇形图形可知,喜欢羽毛球人数占全部调查人数的30%,可以求出调查的总人数,调查总人数=喜欢羽毛球的人数÷喜欢羽毛球占的百分数。
(2)喜欢足球的人数,用总人数减去其它项目的人数即可得到喜欢足球的人数;用喜欢足球的人数÷总人数,得到喜欢足球人数占的百分数,再用喜欢排球的人数÷总人数,就得到喜欢排球占的百分数;再补全统计图。
(3)用喜欢羽毛球的人数减去喜欢足球的人数,再除以喜欢足球的人数,就是该社区喜欢羽毛球人数比喜欢足球人数多百分之几。
【详解】(1)60÷30%=200(人);
(2)200-24-46-60-30
=176-46-60-30
=130-60-30
=70-30
=40(人)
足球:40÷200=0.2=20%
排球:30÷200=0.15=15%
(3)(60-40)÷40
=20÷40
=0.5
=50%
【点睛】本题考查了条形统计图,扇形统计图,正确计算出参与调查的人数;以及一个数比另一个数多百分之几,就用多数的减去少的数再除以少的数即可。
19. 扇形 大学 8900 26800 100%
【分析】(1)扇形统计图是用整个圆表示总数(单位“1”),用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几;
(2)每10万人受教育程度人数最小的是指扇形统计图中占的比重最少的那个,每10万人受教育程度的人数=100000×该受教育程度占的百分比;
(3)每10万人中受教育程度为小学的人数=100000×小学的人数占的百分比;
(4)扇形统计图中各部分的百分比之和是单位“1”。
【详解】(1)这是一幅扇形统计图。
(2)38.8%>26.8%>14.0%>11.5%>8.9%
所以受大学教育的人数最少;
100000×8.9%=8900(人)
(3)100000×26.8%=26800(人)
(4)38.8%+26.8%+14.0%+11.5%+8.9%
=65.6%++14.0%+11.5%+8.9%
=79.6%+11.5%+8.9%
=91.1%+8.9%
=100%
【点睛】本题主要考查扇形统计图的概念和意义,扇形统计图中圆表示整体,即单位“1”,各部分量表示占总量的百分之几。
20.⑴100人
⑵立定跳远:30%;掷实心球:10%
⑶
【详解】(1)观察条形统计图可知,最喜欢跳绳的有200人,观察扇形统计图可知,最喜欢跳绳的占总人数的40%,用最喜欢跳绳的人数÷最喜欢跳绳的人数占总人数的百分比=总人数,然后用总人数×最喜欢仰卧起坐的人数占总人数的百分比=最喜欢仰卧起坐的人数,据此列式解答;
(2)要求最喜欢立定跳远和掷实心球的人数分别占总人数的百分之几?用最喜欢立定跳远的人数÷总人数=最喜欢立定跳远的人数占总人数的百分比,用最喜欢掷实心球的人数÷总人数=最喜欢掷实心球的人数占总人数的百分比,据此列式解答;
(3)根据上面的计算,将条形统计图和扇形统计图补充完整,据此解答。
解:(1)总人数:200÷40%=500(人)
最喜欢仰卧起坐的人数:500×20%=100(人)
答:最喜欢仰卧起坐的有100人。
(2)最喜欢立定跳远的占:150÷500=0.3=30%;
最喜欢掷实心球的占:50÷500=0.1=10%。
答:最喜欢立定跳远的人数占总人数的30%,最喜欢掷实心球的人数占总人数的10%。
(3)根据计算,解答如下:
21.(1)400人。
(2)
【详解】(1)92÷23%=400(人)
答:光明小学六年级共有学生400人。
(2)400﹣92﹣100﹣168=40(人)
光明小学六年级学生有AB型血40人
1﹣23%﹣42%﹣10%=25%
光明小学B型血人数占25%
22.(1)500;100
(2)见详解
【分析】(1)观察条形统计图可知,对“包容”最感兴趣的有150人,观察扇形统计图可知,对“包容”最感兴趣的占调查人数的30%,要求调查人数,用150÷30%;要求最喜欢“尚德”的有几人,用调查的总人数-喜欢其他4项的总人数=最喜欢“尚德”的人数,据此列式解答;
(2)根据上题计算,可以将条形统计图补充完整,然后用喜欢某项内容的人数÷调查的总人数=某项内容占总人数的百分比,据此将扇形统计图补充完整。
【详解】(1)150÷30%=500(人);该校共调查了500人。
500-150-50-125-75
=500-400
=100(人),其中最喜欢“尚德”的有100人。
(2)尚德:100÷500=20%;
守法:50÷500=10%;
卓越:75÷500=15%
画图如下:
【点睛】此题考查了条形统计图和扇形统计图的综合应用,学会根据条件从统计图中找出有效的数学信息是解题关键。
【分层训练】苏教版六年级下册数学第一单元《扇形统计图》基础卷
一、单选题。(共6题;共12分)
1.人离不开水,成年人每天体内47%的水靠喝水获得,39%来自食物含的水,14%来自体内氧化时释放出来的水。最适合选用( )统计图来处理该数据。
A.条形 B.折线 C.扇形
2.医院要反映出一个病人一天的体温变化情况,最好用( )。
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上都可以
3.( )不仅能看出各种数量的多少,而且能呈现数量的增减变化情况。
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
4.开学初,要在六(1)班的48名学生中选出一名同学任班长。民主选举的结果如下表。
姓名 赵小铭 张红 何云飞 李晓勇
票数 24票 12票 7票 5票
如果将这一结果用扇形统计图表示,那么正确表示这一选举结果的是( )。
A. B. C. D.
5.某酒精溶液是由75%的水和25%的酒精形成的.下面图( )能正确地表示这个信息.
A. B. C. D.
6.要反映200毫升牛奶中钙、铁、锌等各种营养成分的含量多少,用( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.复式折线统计图
二、判断题。(共3题;共6分)
7.扇形统计图能清楚地看出数量的多少和数量变化的情况。 ( )
8.医生统计病人体温变化情况,较合适的是选择折线统计图。( )
9.扇形统计图的特点是只能比较清楚地看出各部分量的多少。( )
三、填空题。(共7题;共27分)
10.医生每四个小时给病人测温度变化选用( )统计图,统计住院各科人数时,选用( )
11.( )统计图可以清楚地表示出各部分数量与总数量之间的关系。要表示数量增减变化情况,用( )统计图比较合适。
12.某果园种苹果树面积占总面积的58%,种桔树面积占32%,余下的种桃树,若要制成扇形统计图,其中表示种桃树的面积的扇形圆心角是 度。
13.下图是某学校六年级学生喜欢球类运动的统计图:
(1)喜欢 和 的学生差不多。
(2)有200名学生参加了调查,喜欢足球运动的有 人。
(3)喜欢其他运动的同学占 %。
14.通过学习《科学》,我们知道我国国土面积约960万平方千米,下图是各种地形所占百分比情况.
(1)我国的平原面积是 万平方千米.
(2)我国的盆地面积比山地面积少 平方千米.
15.六年级有50人,每人只能参加一项课外活动,课外活动情况如下图所示。
(1)喜欢打 的人数最多,是 人。
(2)喜欢打 的人数最少,是 人。
(3)喜欢打篮球的有10人,占全班人数的 %。
16.如图是某校六年级(1)班学生为玉树灾区捐款情况抽样调查的条形统计图和扇形统计图。由图可知,六(1)班共有 人;在扇形统计图中,六(1)班捐款15元的人数所占的圆心角度数n的值为 ;若该校六年级学生有800人,据此信息可估计该校六年级捐款总数为 元。
四、解答题。(共6题;共55分)
17.一块蔬菜地中,种着青椒、黄瓜、丝瓜和茄子四种蔬菜.下图表示各种蔬菜的种植面积.
(1)青椒的种植面积占 %.
(2)如果丝瓜种植面积是300平方米,这块蔬菜地的总面积是 平方米.
(3) 的种植面积最大,比茄子面积多 %.
18.某社区为了解居民对足球、篮球、排球、羽毛球和乒乓球这五种球类运动项目的喜爱情况,在社区开展了“我最喜爱的球类运动项目”的随机调查(每位被调查者必须且只能选择最喜爱的一种球类运动项目),并将调查结果进行了统计,绘制成了如图所示的两幅不完整的统计图。
(1)本次调查的总人数是( )人。
(2)将上面的两幅统计图补充完整。
(3)请计算出该社区喜欢羽毛球比足球人数多百分之几?
19.下图是2010年我国人口中每10万人受教育程度人数分布情况。根据有关数据回答下列问题。
(1)这是一幅( )统计图。
(2)每10万人受教育程度人数最小的是( ),大约有( )人。
(3)每10万人中受教育程度为小学的人数是( )人。
(4)所有的百分比之和是( )。
20.补一补。希望小学对学生最喜爱的四个体育运动项目的人数进行了统计,绘制了两种统计图。
⑴最喜欢仰卧起坐的有多少人?
⑵最喜欢立定跳远和掷实心球的人数分别占总人数的百分之几?
⑶请把条形统计图和扇形统计图补充完整。
21.光明小学对六年级全体学生进行了血型统计,王老师根据统计数据制作了一幅扇形统计图和一幅条形统计图。
(1)光明小学六年级共有学生 人。
(2)根据以上数据,把扇形统计图和条形统计图补充完整。
22.太原市提出城市核心价值观:“包容、尚德、守法、诚信、卓越”。新华路小学德育处为了解学生对城市核心价值观中哪一项内容最感兴趣,随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的部分统计图。
请你结合图中信息解答下面的问题:
(1)该校共调查了( )人,其中最喜欢“尚德”的有( )人。
(2)请你把条形统计图和扇形统计图补充完整。
参考答案:
1.C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此解答即可。
【详解】根据统计图的特点可知,成年人每天体内47%的水靠喝水获得,39%来自食物含的水,14%来自体内氧化时释放出来的水,用扇形统计图表示比较合适。
故答案为:C
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
2.B
【分析】折线统计图能清楚的看出数量的增减变化情况,所以观察病人的体温变化情况,最好用折线统计图。
【详解】医院要反映出一个病人一天的体温变化情况,最好用折线统计图。
故答案为:B。
【点睛】此题考查根据实际情况选择统计图,需熟练掌握各种统计图的特点。
3.B
【分析】折线统计图用折线的起伏表示数据的增减变化情况。不仅可以表示数量的多少,而且可以反映数据的增减变化情况。
条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。从条形统计图中很容易看出各种数量的多少。
扇形统计图是用整个圆表示总数(单位“1”),用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几,扇形统计图中各部分的百分比之和是单位“1”。
统计表可以更加清晰、明了地反映数据的情况。
据此选择。
【详解】折线统计图不仅能看出各种数量的多少,而且能呈现数量的增减变化情况。
故答案为:B。
【点睛】此题考查统计图表的选择,掌握各种统计图的特点是解题关键。
4.A
【分析】扇形统计图是用整个圆表示总数单位“1”,用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几,扇形统计图中各部分的百分比之和是单位“1”。本题中把六(1)班总人数(48)人看作单位“1”,根据求一个数是另一个数的百分之几,分别求出四名同学的得票率,然后与4幅统计图进行比较即可。
【详解】赵小铭:24÷48=0.5=50%,即赵小铭的票数是全班同学的50%,即占圆的一半。也就是;
张红:12÷48=0.25=25%,张红的票数是全班同学的25%,即占圆的;
何云飞+李小勇:(7+5)÷48=0.25=25%,两人共占全班人数的25%,即占圆;
首先排除图C、图D,因为这两幅图中都没有表示50%的扇形;图B也没有表示25%的扇形,所以只有图A符合题意。
故答案选:A
【点睛】本题考查扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
5.D
【详解】360°×25%=90°,表示酒精的扇形的圆心角是90°,所以D图正确。
故答案为:D
【点睛】用360°乘酒精占的百分率即可求出表示酒精的扇形的圆心角的度数,然后选择图形即可。
6.C
【分析】扇形统计图能反映部分与整体的关系,据此作答即可。
【详解】反映200毫升牛奶中钙、铁、锌等各种营养成分的含量多少,用扇形统计图比较合适。
故答案为:C。
【点睛】此题考查统计图的选择,掌握各种统计图的特点是解题关键。
7.×
【分析】条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。据此判断。
【详解】折线统计图能清楚地看出数量的多少和数量变化的情况。原题说法错误。
故答案为:×。
【点睛】熟练掌握各种统计图的特点是解题关键。
8.√
【分析】折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况,据此解答。
【详解】医生统计病人体温变化情况,较合适的是选择折线统计图。
故答案为:√
【点睛】掌握折线统计图的特点是解答此题的关键。
9.×
【分析】扇形统计图描述的是各部分所占的百分比,条形统计图描述的是各部分具体的数量。
【详解】扇形统计图的特点是只能清楚地看出各部分所占的百分比。
故原说法错误。
【点睛】本题考查扇形统计图的特征,熟记各类统计图的特征是解答此题的关键。
10. 折线 条形统计图
【详解】略
11. 扇形 折线
【分析】三种统计图特点:条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势;扇形统计图可以显示部分与总体的关系。
【详解】扇形统计图可以清楚地表示出各部分数量与总数量之间的关系。要表示数量增减变化情况,用折线统计图比较合适。
【点睛】熟练掌握各种统计图的特点是解题关键。
12.36
【详解】略
13. 排球 篮球 50 13
【分析】(1)根据每种球喜欢的人数占总人数的百分率判断喜欢哪两种运动的人数差不多;
(2)用参加调查的人数乘喜欢足球运动的百分率即可求出喜欢足球运动的人数;
(3)用1减去已知的4种运动的百分率即可求出喜欢其他运动的同学占总人数的百分率。
【详解】(1)18%和19%差不多,所以喜欢排球和篮球的学生差不多;
(2)200×25%=50(人)
(3)1-(25%+18%+25%+19%)
=1-87%
=13%
14. 115.2 134.4
【详解】略
15. 乒乓球 20 羽毛球 5 20
【分析】根据扇形统计图,占的区域面积最大,则人数最多,占的面积最小,则人数最少,之后用总人数分别乘对应的百分率即可求出对应的人数;喜欢打篮球的人数占全班人数的百分之多少,用喜欢打篮球的人数÷全班人数×100%,把数代入即可求解。
【详解】(1)50×40%=20(人)
喜欢打乒乓球的人数最多,是20人。
(2)50×10%=5(人)
喜欢打羽毛球的人数最少,是5人。
(3)10÷50×100%
=0.2×100%
=20%
【点睛】本题关键是根据扇形统计图的特点,找出单位“1”,进一步理清解答思路,列式的顺序,从而较好的解答问题。
16. 50 72° 7600
【分析】(1)根据由条形统计图提供的数据,求出各捐款数的人数之和就是该班总人数。
(2)捐款15元的人数占总人数的几分之几,扇形的圆心角就是360°的几分之几。
(3)先求出六(1)班平均每人捐款数再乘800即可估计六年级捐款总数。
【详解】(1)六(1)班共有:15+25+10=50(人)
(2)六(1)班捐款15元的人数所占的圆心角度数n的值为:360°×=72°
(3)据此信息可估计该校六年级捐款总数为:
(5×15+10×25+15×10)÷(15+25+10)
=720÷50
=9.5(元)
9.5×800=7600(元)
17. 20 1200 黄瓜 350
【分析】(1)根据题意,将这块蔬菜的总面积看作单位“1”,青椒地的种植面积可用单位“1”分别减去丝瓜、黄瓜、茄子各占总面积的百分数即可;(2)可用丝瓜的面积300平方米除以丝瓜占总面积的25%即可得到蔬菜的总面积,列式解答即可得到答案;(3)根据图示,黄瓜的种植面积最大,可用总的蔬菜地的面积分别乘黄瓜、茄子各占总面积的百分数即可得到黄瓜、茄子的种植面积,再用黄瓜的种植面积减去茄子的种植面积除以茄子的面积乘100%即可.
【详解】(1)1﹣25%﹣10%﹣45%=75%﹣10%﹣45%=65%﹣45%=20%;
故填:20%;
(2)300÷25%=1200(平方米);
故填:1200;
(3)黄瓜的种植面积为:1200×45%=540(平方米),
茄子的种植面积为:1200×10%=120(平方米),
(540﹣120)÷120,=420÷120=3.5=350%;
故填:黄瓜,350%.
故答案为(1)20%,(2)1200,(3)黄瓜,350%.
18.(1)200
(2)
(3)50%
【分析】(1)观察条形统计图可知,喜欢羽毛球的人数有60人,观察扇形图形可知,喜欢羽毛球人数占全部调查人数的30%,可以求出调查的总人数,调查总人数=喜欢羽毛球的人数÷喜欢羽毛球占的百分数。
(2)喜欢足球的人数,用总人数减去其它项目的人数即可得到喜欢足球的人数;用喜欢足球的人数÷总人数,得到喜欢足球人数占的百分数,再用喜欢排球的人数÷总人数,就得到喜欢排球占的百分数;再补全统计图。
(3)用喜欢羽毛球的人数减去喜欢足球的人数,再除以喜欢足球的人数,就是该社区喜欢羽毛球人数比喜欢足球人数多百分之几。
【详解】(1)60÷30%=200(人);
(2)200-24-46-60-30
=176-46-60-30
=130-60-30
=70-30
=40(人)
足球:40÷200=0.2=20%
排球:30÷200=0.15=15%
(3)(60-40)÷40
=20÷40
=0.5
=50%
【点睛】本题考查了条形统计图,扇形统计图,正确计算出参与调查的人数;以及一个数比另一个数多百分之几,就用多数的减去少的数再除以少的数即可。
19. 扇形 大学 8900 26800 100%
【分析】(1)扇形统计图是用整个圆表示总数(单位“1”),用圆内过圆心O点的各个扇形的大小表示各部分量占总量的百分之几;
(2)每10万人受教育程度人数最小的是指扇形统计图中占的比重最少的那个,每10万人受教育程度的人数=100000×该受教育程度占的百分比;
(3)每10万人中受教育程度为小学的人数=100000×小学的人数占的百分比;
(4)扇形统计图中各部分的百分比之和是单位“1”。
【详解】(1)这是一幅扇形统计图。
(2)38.8%>26.8%>14.0%>11.5%>8.9%
所以受大学教育的人数最少;
100000×8.9%=8900(人)
(3)100000×26.8%=26800(人)
(4)38.8%+26.8%+14.0%+11.5%+8.9%
=65.6%++14.0%+11.5%+8.9%
=79.6%+11.5%+8.9%
=91.1%+8.9%
=100%
【点睛】本题主要考查扇形统计图的概念和意义,扇形统计图中圆表示整体,即单位“1”,各部分量表示占总量的百分之几。
20.⑴100人
⑵立定跳远:30%;掷实心球:10%
⑶
【详解】(1)观察条形统计图可知,最喜欢跳绳的有200人,观察扇形统计图可知,最喜欢跳绳的占总人数的40%,用最喜欢跳绳的人数÷最喜欢跳绳的人数占总人数的百分比=总人数,然后用总人数×最喜欢仰卧起坐的人数占总人数的百分比=最喜欢仰卧起坐的人数,据此列式解答;
(2)要求最喜欢立定跳远和掷实心球的人数分别占总人数的百分之几?用最喜欢立定跳远的人数÷总人数=最喜欢立定跳远的人数占总人数的百分比,用最喜欢掷实心球的人数÷总人数=最喜欢掷实心球的人数占总人数的百分比,据此列式解答;
(3)根据上面的计算,将条形统计图和扇形统计图补充完整,据此解答。
解:(1)总人数:200÷40%=500(人)
最喜欢仰卧起坐的人数:500×20%=100(人)
答:最喜欢仰卧起坐的有100人。
(2)最喜欢立定跳远的占:150÷500=0.3=30%;
最喜欢掷实心球的占:50÷500=0.1=10%。
答:最喜欢立定跳远的人数占总人数的30%,最喜欢掷实心球的人数占总人数的10%。
(3)根据计算,解答如下:
21.(1)400人。
(2)
【详解】(1)92÷23%=400(人)
答:光明小学六年级共有学生400人。
(2)400﹣92﹣100﹣168=40(人)
光明小学六年级学生有AB型血40人
1﹣23%﹣42%﹣10%=25%
光明小学B型血人数占25%
22.(1)500;100
(2)见详解
【分析】(1)观察条形统计图可知,对“包容”最感兴趣的有150人,观察扇形统计图可知,对“包容”最感兴趣的占调查人数的30%,要求调查人数,用150÷30%;要求最喜欢“尚德”的有几人,用调查的总人数-喜欢其他4项的总人数=最喜欢“尚德”的人数,据此列式解答;
(2)根据上题计算,可以将条形统计图补充完整,然后用喜欢某项内容的人数÷调查的总人数=某项内容占总人数的百分比,据此将扇形统计图补充完整。
【详解】(1)150÷30%=500(人);该校共调查了500人。
500-150-50-125-75
=500-400
=100(人),其中最喜欢“尚德”的有100人。
(2)尚德:100÷500=20%;
守法:50÷500=10%;
卓越:75÷500=15%
画图如下:
【点睛】此题考查了条形统计图和扇形统计图的综合应用,学会根据条件从统计图中找出有效的数学信息是解题关键。
