苏教版数学五年级下册第二单元《折线统计图》单元测试卷(基础卷)(含解析)
文档属性
| 名称 | 苏教版数学五年级下册第二单元《折线统计图》单元测试卷(基础卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 588.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 21:38:03 | ||
图片预览


文档简介
苏教版数学五年级下册第二单元《折线统计图》单元测试卷(基础卷)
【分层训练】苏教版五年级下册数学第二单元《折线统计图》基础卷
一、选择题。(共9题;共18分)
1.下面情形适合用折线统计图表示的是( )。
A.商场内空调、风扇、吹风机的销售情况 B.班级中喜欢吃香蕉、苹果、桔子、荔枝的人数
C.一天的气温情况 D.班级里小明、小红、小亮、小林四位同学的考试成绩
2.下面是果果8~14岁每年生日时的体重统计表。要表示果果的体重变化情况选用( )更合适。
年龄/岁 8 9 10 11 12 13 14
体重/kg 23 27 30 33 35 42 45
A.条形统计图 B.折线统计图 C.扇形统计图
3.小明骑自行车上学,开始时以正常速度匀速行驶,但行至中途时自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他加快了骑车速度继续匀速行驶,下面是行驶路程s(米)与时间t(分)的关系图,那么符合这个同学行驶情况的图象大致是( )。
A. B.
C. D.
4.要想清楚地表示一个病人一天中的体温变化情况,应选用( )统计图比较合适.
A.条形 B.折线 C.扇形
5.陈红把自己一周的支出情况用扇形统计图表示。下列说法错误的是( )。
A.图中一般不标出具体消费金额
B.图中一般不标出各项消费金额占总消费金额的百分比
C.图中一般标出各项消费金额占总消费金额的百分比
6.下面的四个选项中,对统计描述不正确的是( )。
A.一组数据的平均数有可能比其中的最大数还大。
B.描述本周气温的变化情况,用折线统计图合适。
C.描述书店每月的图书销售数量情况,用条形统计图合适。
D.描述农作物的种植面积占土地总面积的百分比情况,用扇形统计图合适。
7.某企业为了清楚地表示出过去十年的产值变化情况,应选用( )统计图。
A.条形 B.折线 C.扇形 D.其他
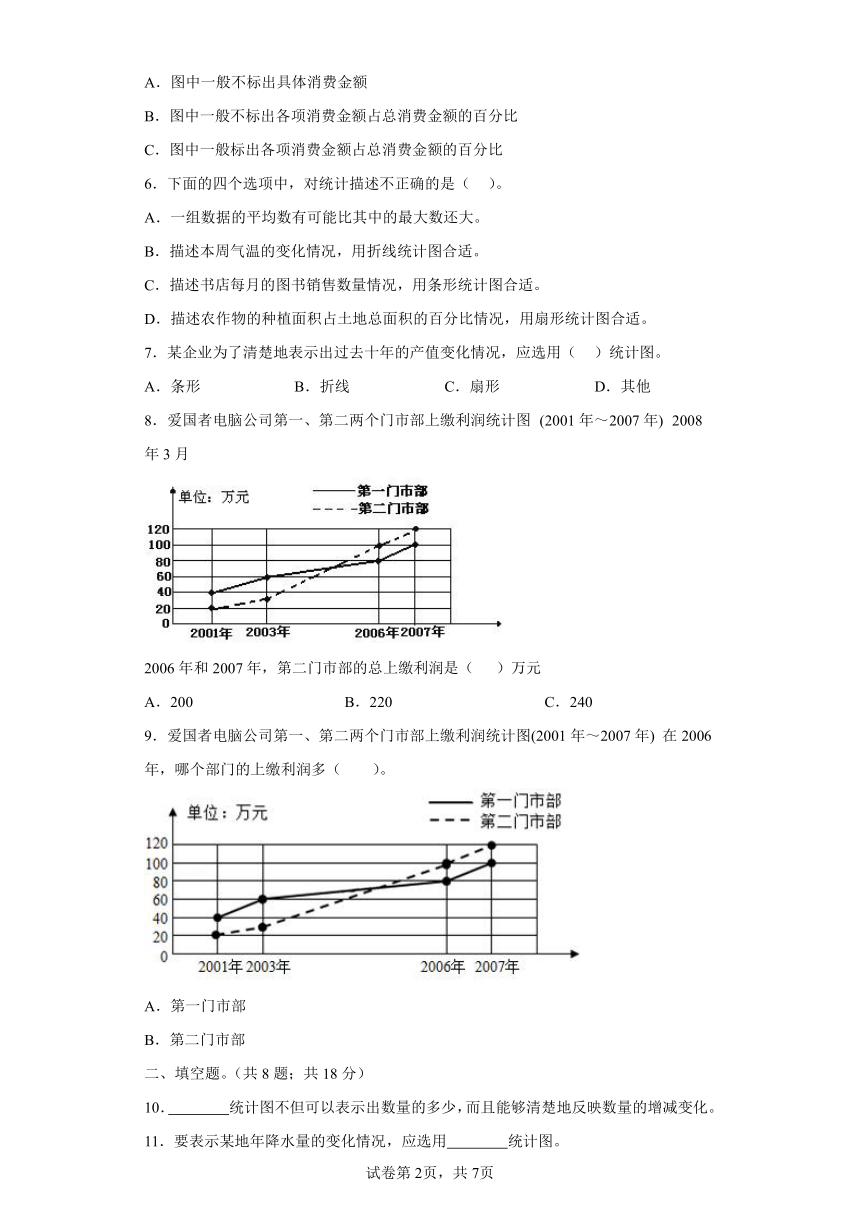
8.爱国者电脑公司第一、第二两个门市部上缴利润统计图 (2001年~2007年) 2008年3月
2006年和2007年,第二门市部的总上缴利润是( )万元
A.200 B.220 C.240
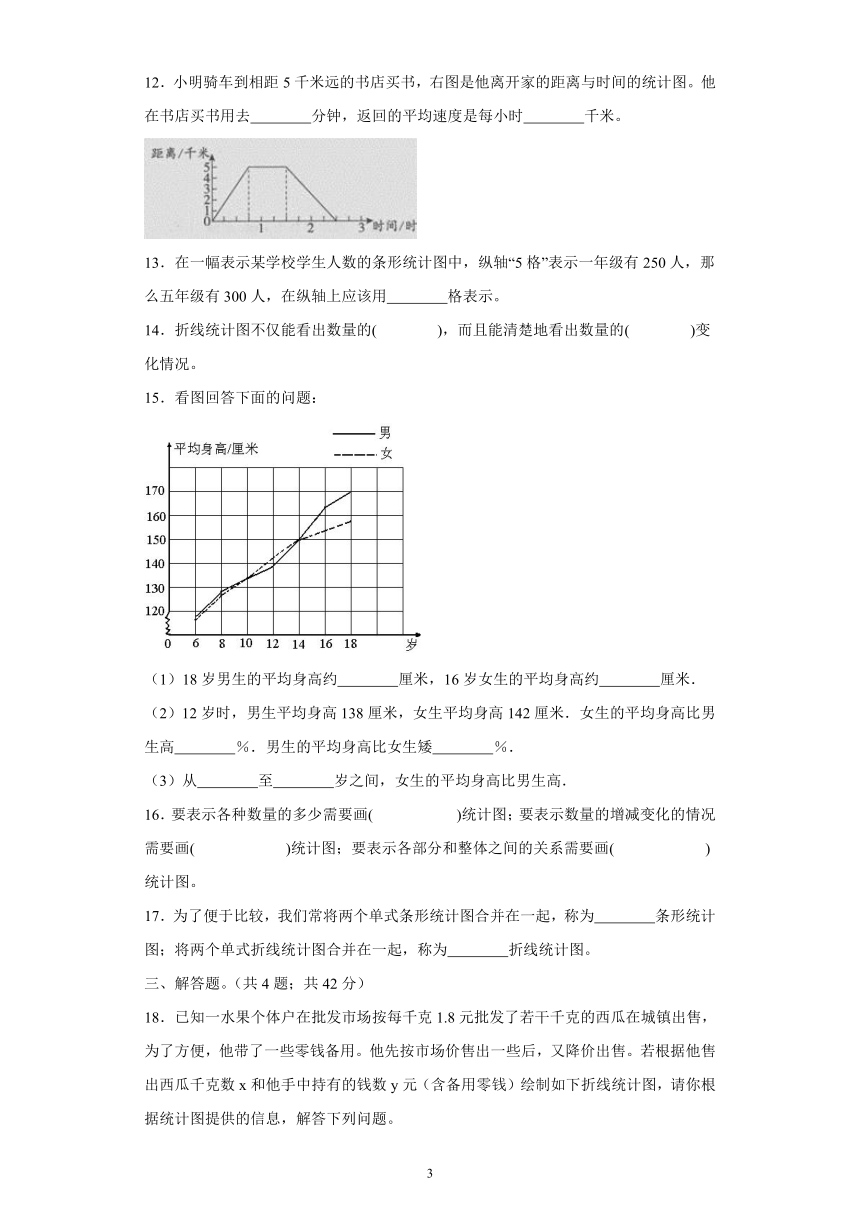
9.爱国者电脑公司第一、第二两个门市部上缴利润统计图(2001年~2007年) 在2006年,哪个部门的上缴利润多( )。
A.第一门市部
B.第二门市部
二、填空题。(共8题;共18分)
10. 统计图不但可以表示出数量的多少,而且能够清楚地反映数量的增减变化。
11.要表示某地年降水量的变化情况,应选用 统计图。
12.小明骑车到相距5千米远的书店买书,右图是他离开家的距离与时间的统计图。他在书店买书用去 分钟,返回的平均速度是每小时 千米。
13.在一幅表示某学校学生人数的条形统计图中,纵轴“5格”表示一年级有250人,那么五年级有300人,在纵轴上应该用 格表示。
14.折线统计图不仅能看出数量的( ),而且能清楚地看出数量的( )变化情况。
15.看图回答下面的问题:
(1)18岁男生的平均身高约 厘米,16岁女生的平均身高约 厘米.
(2)12岁时,男生平均身高138厘米,女生平均身高142厘米.女生的平均身高比男生高 %.男生的平均身高比女生矮 %.
(3)从 至 岁之间,女生的平均身高比男生高.
16.要表示各种数量的多少需要画( )统计图;要表示数量的增减变化的情况需要画( )统计图;要表示各部分和整体之间的关系需要画( )统计图。
17.为了便于比较,我们常将两个单式条形统计图合并在一起,称为 条形统计图;将两个单式折线统计图合并在一起,称为 折线统计图。
三、解答题。(共4题;共42分)
18.已知一水果个体户在批发市场按每千克1.8元批发了若干千克的西瓜在城镇出售,为了方便,他带了一些零钱备用。他先按市场价售出一些后,又降价出售。若根据他售出西瓜千克数x和他手中持有的钱数y元(含备用零钱)绘制如下折线统计图,请你根据统计图提供的信息,解答下列问题。
(1)降价前他每千克西瓜出售的价格是 元。
(2)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了 千克的西瓜。
(3)这位水果个体户一共赚了 元。
19.信息统计。
根据上面统计图提供的数据填空。
(1)枫叶新区2005年的月平均气温,从( )月开始逐渐上升,( )月的月平均气温最高。
(2)枫叶新区2005年的月平均气温,从( )月开始逐渐下降,( )月的月平均气温最低。
(3)( )月与( )月之间的平均气温上升得最快,( )月与( )月之间的平均气温下降得最快。
20.李强收集了南京和哈尔滨2019年4月某一周每天的最高气温,结果如下:
4月 17日 4月 18日 4月 19日 4月 20日 4月 21日 4月 22日 4月 23日
南京 20 23 25 18 25 27 17
哈尔滨 8 13 18 17 19 13 13
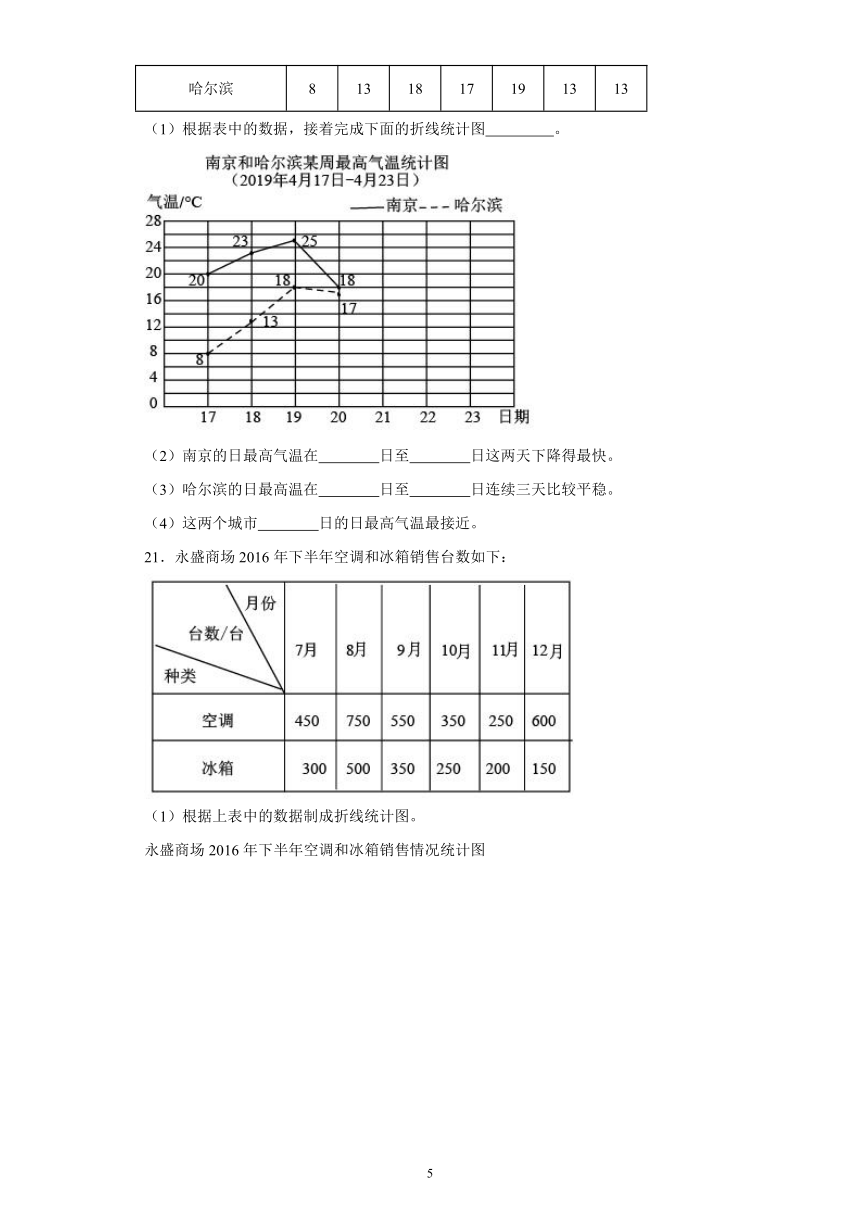
(1)根据表中的数据,接着完成下面的折线统计图 。
(2)南京的日最高气温在 日至 日这两天下降得最快。
(3)哈尔滨的日最高温在 日至 日连续三天比较平稳。
(4)这两个城市 日的日最高气温最接近。
21.永盛商场2016年下半年空调和冰箱销售台数如下:
(1)根据上表中的数据制成折线统计图。
永盛商场2016年下半年空调和冰箱销售情况统计图
(2)回答以下问题。
①空调________月销售量最高,是________台;________月销售量最低,是________台;冰箱________月销售量最高,是________台,________月销售量最低,是________台。
②________月冰箱和空调的销售量相差最大,________月冰箱和空调的销售量相差最小。
(3)如果每台冰箱获利100元,那么这个商场电器城2016年下半年冰箱销售中共获利多少元?
四、综合题。(共2题;共22分)
22.下面是五(2)班周阳和赵娟6~12岁的身高统计图。
(1)9岁时,周阳身高是( )cm,赵娟身高是( )cm,相差( )cm。
(2)( )岁时,周阳和赵娟一样高。
(3)6岁时,( )比( )高( )cm;12岁时,( )比( )高( )cm。
23.根据统计表,完成下列各题。
甲、乙两城市月平均降水量统计表(单位:mm)
月份 1 2 3 4 5 6 7 8 9 10 11 12
甲 5 10 20 25 60 140 180 210 70 30 15 10
乙 20 50 80 160 290 280 210 240 190 65 30 15
(1)根据统计表制作折线统计图,然后看图回答问题。
(2)甲市________月份月平均降水量最高,________月份月平均降水量最低。
(3)乙市________月份月平均降水量最高,________月份月平均降水量最低。
(4)甲市最高与最低月平均降水量相差________mm。
(5)甲、乙两市月平均降水量________月份相差最多,相差________mm。
(6)甲、乙两市月平均降水量相差15mm的是________月和________月。
参考答案:
1.C
【分析】条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况,据此选择。
【详解】A.商场内空调、风扇、吹风机的销售情况适合用条形统计图表示;
B.班级中喜欢吃香蕉、苹果、桔子、荔枝的人数适合用条形统计图表示;
C.一天的气温情况适合用折线统计图表示;
D.班级里小明、小红、小亮、小林四位同学的考试成绩适合用条形统计图表示。
故答案为:C。
【点睛】本题主要考查统计图的选择,牢记条形、折线统计图的特点是解题的关键。
2.B
【分析】折线统计图用折线的起伏表示数据的增减变化情况。果果的体重是在变化的,所以选用折线统计图更合适。
【详解】根据分析可知,要表示果果的体重变化情况选用折线统计图更合适。
故答案为:B。
【点睛】折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。
3.C
【分析】本题直接根据正比例的意义及行程问题的解题方法进行解答即可。
【详解】因为小明上学时的速度是匀速的,所以开始是以直线的形状行驶的,当车子坏掉修车时,小明则是停止的状态,所以中间的时间段则用平的线段表示,修好车后又以匀速行驶,所以后来的速度也要用直线表示。
故答案为:C
【点睛】考查了折线统计图、正比例的意义及行程问题,虽然不难,是个小综合题。
4.B
【详解】略
5.B
【分析】扇形统计图是用整个圆的面积表示总数,用圆内的扇形面积表示各部分数量占总数的百分比.扇形统计图的优点:它可以清楚地表示出部分数量与总数、部分数量与部分数量之间的关系,据此解答。
【详解】陈红把自己一周的支出情况用扇形统计图表示。下列说法错误的是:图中一般不标出各项消费金额占总消费金额的百分比。
故答案为:B。
【点睛】本题考查要点,扇形统计图特点:可以看出各个部分数量与总数之间的关系,通常标出部分量占总量的百分比,据此判断。
6.A
【分析】A.一组数据中平均数比最大数小,比最小数大;
B.折线统计图能清楚地表示出数量的增减变化情况;
C.书店每月的图书销售数量情况只要知道多少即可,条形统计图能清楚地表示出数量的多少;
D.扇形统计图能表示出部分的量和总量之间的关系。
【详解】A.一组数据的平均数有可能比其中的最大数还大,说法错误 ;
B.描述本周气温的变化情况,用折线统计图合适,说法正确;
C.描述书店每月的图书销售数量情况,用条形统计图合适,说法正确;
D.描述农作物的种植面积占土地总面积的百分比情况,用扇形统计图合适,说法正确 。
故答案为:A。
【点睛】此题考查的是学生对平均数的理解,能掌握常用的统计图的特点并熟练运用。
7.B
【分析】折线统计图:用不同位置的点表示数量的多少,并用折线的上升和下降表示数量的增减变化情况,据此解答。
【详解】某企业为了清楚地表示出过去十年的产值变化情况,应选用折线统计图。
故答案为:B
【点睛】折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。
8.B
【详解】对应纵坐标为220万元.
9.B
【详解】略
10.折线
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图的特点不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系;据此解答。
【详解】由分析可知:折线计图不但可以表示出数量的多少,而且能够清楚地反映数量的增减变化。
【点睛】本题主要考查折线、条形统计图的特点,一般来说,如果几个数量是并列的,只要求表示数量的多少时,选条形统计图。如果表示一个量或几个量增减变化和发展变化趋势,则选折线统计图。如果要求表示各部分数量与总数量之间的关系,则选扇形统计图。
11.折线
【分析】条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况,据此选择。
【详解】根据折线统计图的特点可知:要表示某地年降水量的变化情况,应选用折线统计图。
【点睛】本题主要考查统计图的选择,牢记折线、条形统计图的特点是解题的关键。
12. 45 5
【详解】略
13.6
【分析】用250人除以5求出1格表示的人数,然后用300人除以一格表示的人数即可求出格数。
【详解】250÷5=50(人)
300÷50=6(格)
14. 多少 增减
【详解】根据折线统计图的特点可知,折线统计图不仅能看出数量的多少,而且能清楚地看出数量的增减变化情况。
15. 170 155 2.9 2.8 10 14
【分析】折线统计图用折线的起伏表示数据的增减变化情况,不仅可以表示数量的多少,而且可以反映数据的增减变化情况,据此分析,求一个数比另一个数多百分之几,用(一个数-另一个数)÷另一个数,据此列式解答.
【详解】(1)观察统计图可知,18岁男生的平均身高约170厘米,16岁女生的平均身高约155厘米;
(2)(142-138)÷138
=4÷138
≈0.029
=2.9%
(142-138)÷142
=4÷142
≈0.028
=2.8%
(3)观察统计图可知,从10至14岁之间,女生的平均身高比男生高.
故答案为(1)170,155;(2)2.9,2.8;(3)10,14.
16. 条形 折线 扇形
【详解】要表示数量的多少需要画条形统计图,如:想具体了解一年中四个季度每个季度超市的营业额,就用条形统计图。
要表示数量的增减变化情况需要画折线统计图,如:想了解一年四季中超市营业额的变化情况,就用折线统计图。
要表示各部分数量与总数之间的关系需要画扇形统计图。如:想了解一年四季中各季度营业额与全年总营业额的关系,就用扇形统计图。
17. 复式 复式
【分析】根据数据的分类与整理以及统计图表的制作来解答。
【详解】单式条形统计图或单式折线统计图只能表示一种数据;复式条形统计图或复式折线统计图能表示两种或两种以上的数据。
【点睛】此题考查折线统计图、条形统计图的认识。
18. 3.5 120 184
【分析】(1)从图中可以看出,第一段的线段中,纵轴相差330-50=280,横轴相差80,根据单价×数量=总价,因为单价是不变的,所以降价前他每千克西瓜出售的价格就是纵坐标之差除以横坐标之差;
(2)这个人降价后卖出的西瓜的千克数=(450-降价前的价钱)÷(降价前他每千克西瓜出售的价格-每千克下降的钱数),那么他一共批发了西瓜的千克数=降价前卖出的千克数+降价后卖出的西瓜的千克数;
(3)这位水果个体户一共赚了的钱数=西瓜全部售完后他手中的钱-没有卖西瓜前他手中的钱-每千克批发的钱数×他一共批发了西瓜的千克数。
【详解】(1)降价前他每千克西瓜出售的价格是:
(330-50)÷80
=280÷80
=3.5(元)
(2)他一共批发了:
80+(450-330)÷(3.5-0.5)
=80+120÷3
=80+40
=120(千克)
(3)这位水果个体户一共赚了:
450-50-1.8×120
=400-216
=184(元)
【点睛】掌握分析折线统计图的方法,读懂题意是解决问题的关键。
19. 2 8 9 1 4 5 10 11
【分析】(1)折线向上走表示气温升高,折线最高点就是气温最高的月份。
(2)折线向下走表示气温下降,折线最低点就是气温最低的月份。
(3)从图中明显可以看出四月到五月平均气温上升接近两个格,上升得最快;十月到十一月平均气温下降接近两个格,下降得最快。如果不能直接看出来,则需要逐月计算,再比较。
【详解】观察统计图中可以得出:
(1)枫叶新区2005年的月平均气温,从2月开始逐渐上升,8月的月平均气温最高。
(2)枫叶新区2005年的月平均气温,从9月开始逐渐下降,1月的月平均气温最低。
(3)4月与5月之间的平均气温上升得最快,10月与11月之间的平均气温下降得最快。
【点睛】本题是一个关于折线统计图的题目,考查了学生利用统计图中的信息解决实际问题,同时考查了学生观察、分析能力。
20. 见详解 22 23 19 21 20
【分析】(1)根据统计表中的数据,先描点,再连线,最后写上数据。实线表示南京,虚线表示哈尔滨;
(2)两点之间距离最大的两个日期就是下降得最快的;
(3)哈尔滨的日最高温有三天比较平稳的时间是三个点比较接近的地方;
(4)两个地方的两个点比较最接近的两天就是最高气温最接近的时间。
【详解】(1)
(2)南京的日最高气温在22日至23日这两天下降得最快;
(3)哈尔滨的日最高温在19日至21日连续三天比较平稳;
(4)这两个城市20日的日最高气温最接近。
【点睛】此题考查的是对折线统计图的理解和掌握情况,会根据统计图中的信息完成问题。
21.(1)
(2)8;750;11;250;8;500;12;150;12;11
(3)175000元
【分析】(1)复式折线统计图绘制法:先找出所有点的位置,再用不同的线依次连线,并在点上面标上数字;
(2)通过比较,数最大的就是销量最高的,数最小的就是销量最低的;再计算冰箱和空调的销售量差,找出相差最大的和相差最小的,并找出对应的月份;
(3)每台冰箱获利×卖出冰箱的总台数=总获利的钱数。
【详解】(2)①空调8月销售量最高,是750台;11月销售量最低,是250台;冰箱8月销售量最高,是500台,12月销售量最低,是150台;
②12月冰箱和空调的销售量相差最大,11月冰箱和空调的销售量相差最小;
(3)100×(300+500+350+250+200+150)
=100×1750
=175000(元)
答:2016年下半年冰箱销售中共获利175000元。
【点睛】画折线统计图和读折线统计图是解答本题的重点。
22. 134 132 2 10 周阳 赵娟 3 赵娟 周阳 3
【分析】(1)找出9岁实线对应的纵坐标是周阳的身高;虚线对应的纵坐标是赵娟的身高,两者相减就是身高差;(2)当两点重合时表示两人的身高相同,找出重合点的横坐标即可。(3)找出6岁时两人的对应身高,相减;12岁时两人的对应身高,相减。
【详解】(1)9岁时,周阳身高是134cm,赵娟身高是132cm,相差134-132=2(cm)。(2)两点重合之处在10岁时,两人都是138cm。(3)6岁时,周阳身高120cm,赵娟身高117cm,120-117=3(cm),所以周阳比赵娟高3cm;12岁时,周阳身高150cm,赵娟身高153cm,153-150=3(cm)所以赵娟比周阳高3cm。
【点睛】此题考查复式折线统计图,可以清楚的对比看出两者之间的关系和它们各自的变化情况。
23.(1)见详解
(2)8;1
(3)5;12
(4)205
(5)5;230
(6)1;11
【分析】(1)根据统计表制作甲、乙两城市的降水折线统计图;
(2)观察折线的起伏可知,甲市8月份平均降水量最高,1月份平均降水量最低;
(3)观察折线的起伏可知,乙市5月份平均降水量最高,12月份平均降水量最低;
(4)甲市最高月份平均降水量减最低月份平均降水量;
(5)观察折线统计图可知,甲、乙两市月平均降水量5月份相差最多,用乙市5月份平均降水量减甲市5月份平均降水量即可;
(6)观察折线统计图可知,甲、乙两市月平均降水量相差15毫米的是1月份和11月份。
【详解】(1)
(2)甲市8月份平均降水量最高,1月份平均降水量最低;
(3)乙市5月份平均降水量最高,12月份平均降水量最低;
(4)210-5=205(mm);
(5)甲、乙两市5月份平均降水量相差最多,290-60=230(mm;
(6)甲、乙两市月平均降水量相差15mm的是1月份和11月份。
【点睛】本题考查折线统计图的制作,利用统计图解答问题。
【分层训练】苏教版五年级下册数学第二单元《折线统计图》基础卷
一、选择题。(共9题;共18分)
1.下面情形适合用折线统计图表示的是( )。
A.商场内空调、风扇、吹风机的销售情况 B.班级中喜欢吃香蕉、苹果、桔子、荔枝的人数
C.一天的气温情况 D.班级里小明、小红、小亮、小林四位同学的考试成绩
2.下面是果果8~14岁每年生日时的体重统计表。要表示果果的体重变化情况选用( )更合适。
年龄/岁 8 9 10 11 12 13 14
体重/kg 23 27 30 33 35 42 45
A.条形统计图 B.折线统计图 C.扇形统计图
3.小明骑自行车上学,开始时以正常速度匀速行驶,但行至中途时自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他加快了骑车速度继续匀速行驶,下面是行驶路程s(米)与时间t(分)的关系图,那么符合这个同学行驶情况的图象大致是( )。
A. B.
C. D.
4.要想清楚地表示一个病人一天中的体温变化情况,应选用( )统计图比较合适.
A.条形 B.折线 C.扇形
5.陈红把自己一周的支出情况用扇形统计图表示。下列说法错误的是( )。
A.图中一般不标出具体消费金额
B.图中一般不标出各项消费金额占总消费金额的百分比
C.图中一般标出各项消费金额占总消费金额的百分比
6.下面的四个选项中,对统计描述不正确的是( )。
A.一组数据的平均数有可能比其中的最大数还大。
B.描述本周气温的变化情况,用折线统计图合适。
C.描述书店每月的图书销售数量情况,用条形统计图合适。
D.描述农作物的种植面积占土地总面积的百分比情况,用扇形统计图合适。
7.某企业为了清楚地表示出过去十年的产值变化情况,应选用( )统计图。
A.条形 B.折线 C.扇形 D.其他
8.爱国者电脑公司第一、第二两个门市部上缴利润统计图 (2001年~2007年) 2008年3月
2006年和2007年,第二门市部的总上缴利润是( )万元
A.200 B.220 C.240
9.爱国者电脑公司第一、第二两个门市部上缴利润统计图(2001年~2007年) 在2006年,哪个部门的上缴利润多( )。
A.第一门市部
B.第二门市部
二、填空题。(共8题;共18分)
10. 统计图不但可以表示出数量的多少,而且能够清楚地反映数量的增减变化。
11.要表示某地年降水量的变化情况,应选用 统计图。
12.小明骑车到相距5千米远的书店买书,右图是他离开家的距离与时间的统计图。他在书店买书用去 分钟,返回的平均速度是每小时 千米。
13.在一幅表示某学校学生人数的条形统计图中,纵轴“5格”表示一年级有250人,那么五年级有300人,在纵轴上应该用 格表示。
14.折线统计图不仅能看出数量的( ),而且能清楚地看出数量的( )变化情况。
15.看图回答下面的问题:
(1)18岁男生的平均身高约 厘米,16岁女生的平均身高约 厘米.
(2)12岁时,男生平均身高138厘米,女生平均身高142厘米.女生的平均身高比男生高 %.男生的平均身高比女生矮 %.
(3)从 至 岁之间,女生的平均身高比男生高.
16.要表示各种数量的多少需要画( )统计图;要表示数量的增减变化的情况需要画( )统计图;要表示各部分和整体之间的关系需要画( )统计图。
17.为了便于比较,我们常将两个单式条形统计图合并在一起,称为 条形统计图;将两个单式折线统计图合并在一起,称为 折线统计图。
三、解答题。(共4题;共42分)
18.已知一水果个体户在批发市场按每千克1.8元批发了若干千克的西瓜在城镇出售,为了方便,他带了一些零钱备用。他先按市场价售出一些后,又降价出售。若根据他售出西瓜千克数x和他手中持有的钱数y元(含备用零钱)绘制如下折线统计图,请你根据统计图提供的信息,解答下列问题。
(1)降价前他每千克西瓜出售的价格是 元。
(2)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了 千克的西瓜。
(3)这位水果个体户一共赚了 元。
19.信息统计。
根据上面统计图提供的数据填空。
(1)枫叶新区2005年的月平均气温,从( )月开始逐渐上升,( )月的月平均气温最高。
(2)枫叶新区2005年的月平均气温,从( )月开始逐渐下降,( )月的月平均气温最低。
(3)( )月与( )月之间的平均气温上升得最快,( )月与( )月之间的平均气温下降得最快。
20.李强收集了南京和哈尔滨2019年4月某一周每天的最高气温,结果如下:
4月 17日 4月 18日 4月 19日 4月 20日 4月 21日 4月 22日 4月 23日
南京 20 23 25 18 25 27 17
哈尔滨 8 13 18 17 19 13 13
(1)根据表中的数据,接着完成下面的折线统计图 。
(2)南京的日最高气温在 日至 日这两天下降得最快。
(3)哈尔滨的日最高温在 日至 日连续三天比较平稳。
(4)这两个城市 日的日最高气温最接近。
21.永盛商场2016年下半年空调和冰箱销售台数如下:
(1)根据上表中的数据制成折线统计图。
永盛商场2016年下半年空调和冰箱销售情况统计图
(2)回答以下问题。
①空调________月销售量最高,是________台;________月销售量最低,是________台;冰箱________月销售量最高,是________台,________月销售量最低,是________台。
②________月冰箱和空调的销售量相差最大,________月冰箱和空调的销售量相差最小。
(3)如果每台冰箱获利100元,那么这个商场电器城2016年下半年冰箱销售中共获利多少元?
四、综合题。(共2题;共22分)
22.下面是五(2)班周阳和赵娟6~12岁的身高统计图。
(1)9岁时,周阳身高是( )cm,赵娟身高是( )cm,相差( )cm。
(2)( )岁时,周阳和赵娟一样高。
(3)6岁时,( )比( )高( )cm;12岁时,( )比( )高( )cm。
23.根据统计表,完成下列各题。
甲、乙两城市月平均降水量统计表(单位:mm)
月份 1 2 3 4 5 6 7 8 9 10 11 12
甲 5 10 20 25 60 140 180 210 70 30 15 10
乙 20 50 80 160 290 280 210 240 190 65 30 15
(1)根据统计表制作折线统计图,然后看图回答问题。
(2)甲市________月份月平均降水量最高,________月份月平均降水量最低。
(3)乙市________月份月平均降水量最高,________月份月平均降水量最低。
(4)甲市最高与最低月平均降水量相差________mm。
(5)甲、乙两市月平均降水量________月份相差最多,相差________mm。
(6)甲、乙两市月平均降水量相差15mm的是________月和________月。
参考答案:
1.C
【分析】条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况,据此选择。
【详解】A.商场内空调、风扇、吹风机的销售情况适合用条形统计图表示;
B.班级中喜欢吃香蕉、苹果、桔子、荔枝的人数适合用条形统计图表示;
C.一天的气温情况适合用折线统计图表示;
D.班级里小明、小红、小亮、小林四位同学的考试成绩适合用条形统计图表示。
故答案为:C。
【点睛】本题主要考查统计图的选择,牢记条形、折线统计图的特点是解题的关键。
2.B
【分析】折线统计图用折线的起伏表示数据的增减变化情况。果果的体重是在变化的,所以选用折线统计图更合适。
【详解】根据分析可知,要表示果果的体重变化情况选用折线统计图更合适。
故答案为:B。
【点睛】折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。
3.C
【分析】本题直接根据正比例的意义及行程问题的解题方法进行解答即可。
【详解】因为小明上学时的速度是匀速的,所以开始是以直线的形状行驶的,当车子坏掉修车时,小明则是停止的状态,所以中间的时间段则用平的线段表示,修好车后又以匀速行驶,所以后来的速度也要用直线表示。
故答案为:C
【点睛】考查了折线统计图、正比例的意义及行程问题,虽然不难,是个小综合题。
4.B
【详解】略
5.B
【分析】扇形统计图是用整个圆的面积表示总数,用圆内的扇形面积表示各部分数量占总数的百分比.扇形统计图的优点:它可以清楚地表示出部分数量与总数、部分数量与部分数量之间的关系,据此解答。
【详解】陈红把自己一周的支出情况用扇形统计图表示。下列说法错误的是:图中一般不标出各项消费金额占总消费金额的百分比。
故答案为:B。
【点睛】本题考查要点,扇形统计图特点:可以看出各个部分数量与总数之间的关系,通常标出部分量占总量的百分比,据此判断。
6.A
【分析】A.一组数据中平均数比最大数小,比最小数大;
B.折线统计图能清楚地表示出数量的增减变化情况;
C.书店每月的图书销售数量情况只要知道多少即可,条形统计图能清楚地表示出数量的多少;
D.扇形统计图能表示出部分的量和总量之间的关系。
【详解】A.一组数据的平均数有可能比其中的最大数还大,说法错误 ;
B.描述本周气温的变化情况,用折线统计图合适,说法正确;
C.描述书店每月的图书销售数量情况,用条形统计图合适,说法正确;
D.描述农作物的种植面积占土地总面积的百分比情况,用扇形统计图合适,说法正确 。
故答案为:A。
【点睛】此题考查的是学生对平均数的理解,能掌握常用的统计图的特点并熟练运用。
7.B
【分析】折线统计图:用不同位置的点表示数量的多少,并用折线的上升和下降表示数量的增减变化情况,据此解答。
【详解】某企业为了清楚地表示出过去十年的产值变化情况,应选用折线统计图。
故答案为:B
【点睛】折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。
8.B
【详解】对应纵坐标为220万元.
9.B
【详解】略
10.折线
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图的特点不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系;据此解答。
【详解】由分析可知:折线计图不但可以表示出数量的多少,而且能够清楚地反映数量的增减变化。
【点睛】本题主要考查折线、条形统计图的特点,一般来说,如果几个数量是并列的,只要求表示数量的多少时,选条形统计图。如果表示一个量或几个量增减变化和发展变化趋势,则选折线统计图。如果要求表示各部分数量与总数量之间的关系,则选扇形统计图。
11.折线
【分析】条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况,据此选择。
【详解】根据折线统计图的特点可知:要表示某地年降水量的变化情况,应选用折线统计图。
【点睛】本题主要考查统计图的选择,牢记折线、条形统计图的特点是解题的关键。
12. 45 5
【详解】略
13.6
【分析】用250人除以5求出1格表示的人数,然后用300人除以一格表示的人数即可求出格数。
【详解】250÷5=50(人)
300÷50=6(格)
14. 多少 增减
【详解】根据折线统计图的特点可知,折线统计图不仅能看出数量的多少,而且能清楚地看出数量的增减变化情况。
15. 170 155 2.9 2.8 10 14
【分析】折线统计图用折线的起伏表示数据的增减变化情况,不仅可以表示数量的多少,而且可以反映数据的增减变化情况,据此分析,求一个数比另一个数多百分之几,用(一个数-另一个数)÷另一个数,据此列式解答.
【详解】(1)观察统计图可知,18岁男生的平均身高约170厘米,16岁女生的平均身高约155厘米;
(2)(142-138)÷138
=4÷138
≈0.029
=2.9%
(142-138)÷142
=4÷142
≈0.028
=2.8%
(3)观察统计图可知,从10至14岁之间,女生的平均身高比男生高.
故答案为(1)170,155;(2)2.9,2.8;(3)10,14.
16. 条形 折线 扇形
【详解】要表示数量的多少需要画条形统计图,如:想具体了解一年中四个季度每个季度超市的营业额,就用条形统计图。
要表示数量的增减变化情况需要画折线统计图,如:想了解一年四季中超市营业额的变化情况,就用折线统计图。
要表示各部分数量与总数之间的关系需要画扇形统计图。如:想了解一年四季中各季度营业额与全年总营业额的关系,就用扇形统计图。
17. 复式 复式
【分析】根据数据的分类与整理以及统计图表的制作来解答。
【详解】单式条形统计图或单式折线统计图只能表示一种数据;复式条形统计图或复式折线统计图能表示两种或两种以上的数据。
【点睛】此题考查折线统计图、条形统计图的认识。
18. 3.5 120 184
【分析】(1)从图中可以看出,第一段的线段中,纵轴相差330-50=280,横轴相差80,根据单价×数量=总价,因为单价是不变的,所以降价前他每千克西瓜出售的价格就是纵坐标之差除以横坐标之差;
(2)这个人降价后卖出的西瓜的千克数=(450-降价前的价钱)÷(降价前他每千克西瓜出售的价格-每千克下降的钱数),那么他一共批发了西瓜的千克数=降价前卖出的千克数+降价后卖出的西瓜的千克数;
(3)这位水果个体户一共赚了的钱数=西瓜全部售完后他手中的钱-没有卖西瓜前他手中的钱-每千克批发的钱数×他一共批发了西瓜的千克数。
【详解】(1)降价前他每千克西瓜出售的价格是:
(330-50)÷80
=280÷80
=3.5(元)
(2)他一共批发了:
80+(450-330)÷(3.5-0.5)
=80+120÷3
=80+40
=120(千克)
(3)这位水果个体户一共赚了:
450-50-1.8×120
=400-216
=184(元)
【点睛】掌握分析折线统计图的方法,读懂题意是解决问题的关键。
19. 2 8 9 1 4 5 10 11
【分析】(1)折线向上走表示气温升高,折线最高点就是气温最高的月份。
(2)折线向下走表示气温下降,折线最低点就是气温最低的月份。
(3)从图中明显可以看出四月到五月平均气温上升接近两个格,上升得最快;十月到十一月平均气温下降接近两个格,下降得最快。如果不能直接看出来,则需要逐月计算,再比较。
【详解】观察统计图中可以得出:
(1)枫叶新区2005年的月平均气温,从2月开始逐渐上升,8月的月平均气温最高。
(2)枫叶新区2005年的月平均气温,从9月开始逐渐下降,1月的月平均气温最低。
(3)4月与5月之间的平均气温上升得最快,10月与11月之间的平均气温下降得最快。
【点睛】本题是一个关于折线统计图的题目,考查了学生利用统计图中的信息解决实际问题,同时考查了学生观察、分析能力。
20. 见详解 22 23 19 21 20
【分析】(1)根据统计表中的数据,先描点,再连线,最后写上数据。实线表示南京,虚线表示哈尔滨;
(2)两点之间距离最大的两个日期就是下降得最快的;
(3)哈尔滨的日最高温有三天比较平稳的时间是三个点比较接近的地方;
(4)两个地方的两个点比较最接近的两天就是最高气温最接近的时间。
【详解】(1)
(2)南京的日最高气温在22日至23日这两天下降得最快;
(3)哈尔滨的日最高温在19日至21日连续三天比较平稳;
(4)这两个城市20日的日最高气温最接近。
【点睛】此题考查的是对折线统计图的理解和掌握情况,会根据统计图中的信息完成问题。
21.(1)
(2)8;750;11;250;8;500;12;150;12;11
(3)175000元
【分析】(1)复式折线统计图绘制法:先找出所有点的位置,再用不同的线依次连线,并在点上面标上数字;
(2)通过比较,数最大的就是销量最高的,数最小的就是销量最低的;再计算冰箱和空调的销售量差,找出相差最大的和相差最小的,并找出对应的月份;
(3)每台冰箱获利×卖出冰箱的总台数=总获利的钱数。
【详解】(2)①空调8月销售量最高,是750台;11月销售量最低,是250台;冰箱8月销售量最高,是500台,12月销售量最低,是150台;
②12月冰箱和空调的销售量相差最大,11月冰箱和空调的销售量相差最小;
(3)100×(300+500+350+250+200+150)
=100×1750
=175000(元)
答:2016年下半年冰箱销售中共获利175000元。
【点睛】画折线统计图和读折线统计图是解答本题的重点。
22. 134 132 2 10 周阳 赵娟 3 赵娟 周阳 3
【分析】(1)找出9岁实线对应的纵坐标是周阳的身高;虚线对应的纵坐标是赵娟的身高,两者相减就是身高差;(2)当两点重合时表示两人的身高相同,找出重合点的横坐标即可。(3)找出6岁时两人的对应身高,相减;12岁时两人的对应身高,相减。
【详解】(1)9岁时,周阳身高是134cm,赵娟身高是132cm,相差134-132=2(cm)。(2)两点重合之处在10岁时,两人都是138cm。(3)6岁时,周阳身高120cm,赵娟身高117cm,120-117=3(cm),所以周阳比赵娟高3cm;12岁时,周阳身高150cm,赵娟身高153cm,153-150=3(cm)所以赵娟比周阳高3cm。
【点睛】此题考查复式折线统计图,可以清楚的对比看出两者之间的关系和它们各自的变化情况。
23.(1)见详解
(2)8;1
(3)5;12
(4)205
(5)5;230
(6)1;11
【分析】(1)根据统计表制作甲、乙两城市的降水折线统计图;
(2)观察折线的起伏可知,甲市8月份平均降水量最高,1月份平均降水量最低;
(3)观察折线的起伏可知,乙市5月份平均降水量最高,12月份平均降水量最低;
(4)甲市最高月份平均降水量减最低月份平均降水量;
(5)观察折线统计图可知,甲、乙两市月平均降水量5月份相差最多,用乙市5月份平均降水量减甲市5月份平均降水量即可;
(6)观察折线统计图可知,甲、乙两市月平均降水量相差15毫米的是1月份和11月份。
【详解】(1)
(2)甲市8月份平均降水量最高,1月份平均降水量最低;
(3)乙市5月份平均降水量最高,12月份平均降水量最低;
(4)210-5=205(mm);
(5)甲、乙两市5月份平均降水量相差最多,290-60=230(mm;
(6)甲、乙两市月平均降水量相差15mm的是1月份和11月份。
【点睛】本题考查折线统计图的制作,利用统计图解答问题。
