第29章 投影与视图素养评估卷(含答案)
文档属性
| 名称 | 第29章 投影与视图素养评估卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
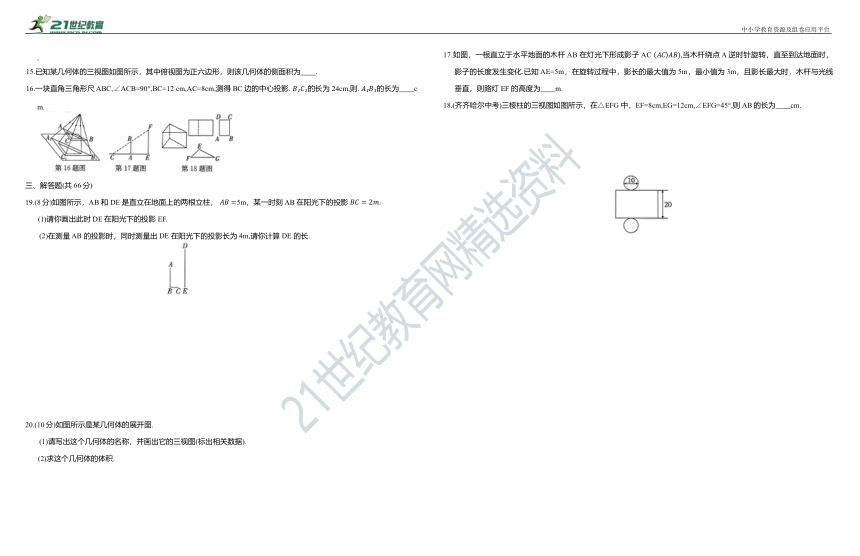
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 09:25:51 | ||
图片预览

文档简介
第29章 投影与视图 素养评估卷
时间:90分钟 满分:120分
一、选择题(每小题3分,共30分)
1.(抚顺中考)下列物体的左视图是圆的是( )
2.(宁波中考)如图,下列关于物体的主视图画法正确的是( )
3.正方形的正投影不可能是( )
A.线段 B.矩形 C.正方形 D.梯形
4.如图是一个几何体的三视图,则这个几何体是( )
5.胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测.根据胡老师给出的方向标,猜测比较合理的是( )
A.小明:“早上8点” B.小亮:“中午12点”
C.小刚:“下午5点” D.小红:“什么时间都行”
6.如图,一块三角尺在灯光照射下形成投影,三角尺与其投影的相似比为2:5,且三角尺的一边长为8cm,则投影三角尺的对应边长为( )
A.20cm B. 10cm C.8cm D.3. 2cm
7.如图是由10个同样大小的小正方体摆成的几何体.若将小正方体①移走,则关于新几何体的三视图描述正确的是( )
A.俯视图不变,左视图不变 B.主视图改变,左视图改变
C.俯视图不变,主视图不变 D.主视图改变,俯视图改变
8.已知某几何体的三视图如图所示,则该几何体的侧面展开图的圆心角的度数为( )
A.214° B.215° C.216° D.217°
9.已知一个组合体是由几个相同的正方体一起组成的,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是( )
A.10 B.9 C.8 D.7
10.如图,空心卷筒纸的高度为 12cm,外径(直径)为 10cm,内径为4cm,在比例尺为1:4的三视图中,其主视图的面积是( )
二、填空题(每小题3分,共24分)
11.广场上一个大型艺术字板块在地上的投影如图所示,则该投影属于 .(填“平行投影”或“中心投影”)
12.如图,长方体的一个底面 ABCD 在投影面 P上,M,N 分别是侧棱 BF,CG 的中点,矩形 EFGH 与矩形EMNH 的投影都是矩形 ABCD,设它们的面积分别是、 则 ,S 的关系是 .(用“>”“<”或“=”连起来)
13.一个几何体由12个大小相同的小立方块搭成,从上面看到的这个几何体的形状图如图所示.若小正方形中的数字表示在该位置小立方块的个数,则从正面看,一共能看到 个小立方块.(被遮挡的不计)
3 3
3 2 1
14.如图,在A 时测得某树的影长为4m,B时又测得该树的影长为 16 m,若两次 日 照的光线互相垂直,则树 的 高度为
15.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 .
16.一块直角三角形尺 ABC,∠ACB=90°,BC=12 cm,AC=8cm,测得 BC边的中心投影. 的长为24cm,则. 的长为 cm.
17.如图,一根直立于水平地面的木杆AB 在灯光下形成影子AC 当木杆绕点 A 逆时针旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为 5m,最小值为3m,且影长最大时,木杆与光线垂直,则路灯 EF 的高度为 m.
中小学教育资源及组卷应用平台
18.(齐齐哈尔中考)三棱柱的三视图如图所示,在△EFG 中,EF=8cm,EG=12cm,∠EFG=45°,则AB的长为 cm.
三、解答题(共66分)
19.(8分)如图所示,AB 和 DE 是直立在地面上的两根立柱, 5m,某一时刻 AB 在阳光下的投影
(1)请你画出此时DE 在阳光下的投影EF.
(2)在测量 AB 的投影时,同时测量出 DE 在阳光下的投影长为 4m,请你计算DE 的长.
20.(10分)如图所示是某几何体的展开图.
(1)请写出这个几何体的名称,并画出它的三视图(标出相关数据).
(2)求这个几何体的体积.
21.(12分)由大小相同的小立方块搭成的几何体如图①.
(1)请在图②的方格中画出该几何体的俯视图和左视图.
(2)用小立方块搭一个几何体,使得它的俯视图和左视图与
(1)所画的一致,则搭这样的几何体最少要 个小立方块,最多要 个小立方块.
(3)将此几何体露在外面的部分涂上油漆(不包含底面),其中两面涂色的小立方块有多少个
22.(12分)有一个几何体的形状为直三棱柱,如图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据.
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的表面积.
23.(12分)如图所示,阳光通过窗口照到教室内,竖直窗框在地面上留下 2.1m长的影子,已知窗框的影子DE到窗下墙脚的距离 窗口底边离地面的距离 1.2m,试求窗口的高度(即 AB 的长).
24.(12分)一天晚上,李明和张龙利用灯光下的影子长来测量一路灯 D的高度.如图,当李明走到点A 处时,张龙测得李明直立时身高 AM 与其影子长AE 正好相等;接着李明沿 AC方向继续向前走,走到点 B 处时,李明直立时身高 BN 的影子恰好是线段AB,并测得 .已知李明直立时的身高为1.75m,求路灯的高度CD.(结果精确到0.1m)
第二十九章素养评估卷
1. A 2. C 3. D 4. B 5. C 6. A 7. A
8. C [解析]由三视图可知,该几何体为圆锥.由三视图数据可知,圆锥的底面圆的直径为6、半径为3,高为4,则母线长为 设该几何体的侧面展开图的圆心角的度数为 n,则 解得n=216°.
9. B 10. D
11.中心投影 13.8 1 4.8m 1 5.108
[解析]∵∠ACB=90°,BC=12cm,AC=8cm,B C 即 故答案为
17.7.5 18.4
19.解:(1)略. (2)∵AC∥DF,∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF, 即 ,f解得 DE=10,即DE 的长为 10 m.
20.解:(1)圆柱,它的三视图如图所示.
(2)这个几何体的体积为
21.解:(1)如图所示.
(2)9 14 (3)两面涂色的小立方块有2个.
22.解:(1)略. (2)由勾股定理,得主视图中直角三角形的斜边长为10厘米, (平方厘米), 6+10)×3=72(平方厘米), Sa=72+48=120(平方厘米).答:这个几何体的表面积是120平方厘米.
23.解:连接AB,由于阳光是平行光线,即AE∥BD,所以∠AEC=∠BDC.又因为∠BCD 是公共角,所以△AEC∽△BDC,从而有 因为. AC=AB+BC,CD=CE-DE,CE=3.9m,DE=2. 1m,BC=1.2m,所以 解得 AB=1.4m.所以窗口的高度为 1.4m.
24.解:设CD长为x m.∵AM⊥EC,CD⊥EC,BN⊥EC,EA=AM,∴AM∥CD,BN∥CD,∴EC=CD=x m,△ABN∽ 即 解得x=6.125≈6.1.∴路灯的高度CD约为6.1m。
时间:90分钟 满分:120分
一、选择题(每小题3分,共30分)
1.(抚顺中考)下列物体的左视图是圆的是( )
2.(宁波中考)如图,下列关于物体的主视图画法正确的是( )
3.正方形的正投影不可能是( )
A.线段 B.矩形 C.正方形 D.梯形
4.如图是一个几何体的三视图,则这个几何体是( )
5.胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测.根据胡老师给出的方向标,猜测比较合理的是( )
A.小明:“早上8点” B.小亮:“中午12点”
C.小刚:“下午5点” D.小红:“什么时间都行”
6.如图,一块三角尺在灯光照射下形成投影,三角尺与其投影的相似比为2:5,且三角尺的一边长为8cm,则投影三角尺的对应边长为( )
A.20cm B. 10cm C.8cm D.3. 2cm
7.如图是由10个同样大小的小正方体摆成的几何体.若将小正方体①移走,则关于新几何体的三视图描述正确的是( )
A.俯视图不变,左视图不变 B.主视图改变,左视图改变
C.俯视图不变,主视图不变 D.主视图改变,俯视图改变
8.已知某几何体的三视图如图所示,则该几何体的侧面展开图的圆心角的度数为( )
A.214° B.215° C.216° D.217°
9.已知一个组合体是由几个相同的正方体一起组成的,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是( )
A.10 B.9 C.8 D.7
10.如图,空心卷筒纸的高度为 12cm,外径(直径)为 10cm,内径为4cm,在比例尺为1:4的三视图中,其主视图的面积是( )
二、填空题(每小题3分,共24分)
11.广场上一个大型艺术字板块在地上的投影如图所示,则该投影属于 .(填“平行投影”或“中心投影”)
12.如图,长方体的一个底面 ABCD 在投影面 P上,M,N 分别是侧棱 BF,CG 的中点,矩形 EFGH 与矩形EMNH 的投影都是矩形 ABCD,设它们的面积分别是、 则 ,S 的关系是 .(用“>”“<”或“=”连起来)
13.一个几何体由12个大小相同的小立方块搭成,从上面看到的这个几何体的形状图如图所示.若小正方形中的数字表示在该位置小立方块的个数,则从正面看,一共能看到 个小立方块.(被遮挡的不计)
3 3
3 2 1
14.如图,在A 时测得某树的影长为4m,B时又测得该树的影长为 16 m,若两次 日 照的光线互相垂直,则树 的 高度为
15.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 .
16.一块直角三角形尺 ABC,∠ACB=90°,BC=12 cm,AC=8cm,测得 BC边的中心投影. 的长为24cm,则. 的长为 cm.
17.如图,一根直立于水平地面的木杆AB 在灯光下形成影子AC 当木杆绕点 A 逆时针旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为 5m,最小值为3m,且影长最大时,木杆与光线垂直,则路灯 EF 的高度为 m.
中小学教育资源及组卷应用平台
18.(齐齐哈尔中考)三棱柱的三视图如图所示,在△EFG 中,EF=8cm,EG=12cm,∠EFG=45°,则AB的长为 cm.
三、解答题(共66分)
19.(8分)如图所示,AB 和 DE 是直立在地面上的两根立柱, 5m,某一时刻 AB 在阳光下的投影
(1)请你画出此时DE 在阳光下的投影EF.
(2)在测量 AB 的投影时,同时测量出 DE 在阳光下的投影长为 4m,请你计算DE 的长.
20.(10分)如图所示是某几何体的展开图.
(1)请写出这个几何体的名称,并画出它的三视图(标出相关数据).
(2)求这个几何体的体积.
21.(12分)由大小相同的小立方块搭成的几何体如图①.
(1)请在图②的方格中画出该几何体的俯视图和左视图.
(2)用小立方块搭一个几何体,使得它的俯视图和左视图与
(1)所画的一致,则搭这样的几何体最少要 个小立方块,最多要 个小立方块.
(3)将此几何体露在外面的部分涂上油漆(不包含底面),其中两面涂色的小立方块有多少个
22.(12分)有一个几何体的形状为直三棱柱,如图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据.
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的表面积.
23.(12分)如图所示,阳光通过窗口照到教室内,竖直窗框在地面上留下 2.1m长的影子,已知窗框的影子DE到窗下墙脚的距离 窗口底边离地面的距离 1.2m,试求窗口的高度(即 AB 的长).
24.(12分)一天晚上,李明和张龙利用灯光下的影子长来测量一路灯 D的高度.如图,当李明走到点A 处时,张龙测得李明直立时身高 AM 与其影子长AE 正好相等;接着李明沿 AC方向继续向前走,走到点 B 处时,李明直立时身高 BN 的影子恰好是线段AB,并测得 .已知李明直立时的身高为1.75m,求路灯的高度CD.(结果精确到0.1m)
第二十九章素养评估卷
1. A 2. C 3. D 4. B 5. C 6. A 7. A
8. C [解析]由三视图可知,该几何体为圆锥.由三视图数据可知,圆锥的底面圆的直径为6、半径为3,高为4,则母线长为 设该几何体的侧面展开图的圆心角的度数为 n,则 解得n=216°.
9. B 10. D
11.中心投影 13.8 1 4.8m 1 5.108
[解析]∵∠ACB=90°,BC=12cm,AC=8cm,B C 即 故答案为
17.7.5 18.4
19.解:(1)略. (2)∵AC∥DF,∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF, 即 ,f解得 DE=10,即DE 的长为 10 m.
20.解:(1)圆柱,它的三视图如图所示.
(2)这个几何体的体积为
21.解:(1)如图所示.
(2)9 14 (3)两面涂色的小立方块有2个.
22.解:(1)略. (2)由勾股定理,得主视图中直角三角形的斜边长为10厘米, (平方厘米), 6+10)×3=72(平方厘米), Sa=72+48=120(平方厘米).答:这个几何体的表面积是120平方厘米.
23.解:连接AB,由于阳光是平行光线,即AE∥BD,所以∠AEC=∠BDC.又因为∠BCD 是公共角,所以△AEC∽△BDC,从而有 因为. AC=AB+BC,CD=CE-DE,CE=3.9m,DE=2. 1m,BC=1.2m,所以 解得 AB=1.4m.所以窗口的高度为 1.4m.
24.解:设CD长为x m.∵AM⊥EC,CD⊥EC,BN⊥EC,EA=AM,∴AM∥CD,BN∥CD,∴EC=CD=x m,△ABN∽ 即 解得x=6.125≈6.1.∴路灯的高度CD约为6.1m。
