一元三次函数(辽宁省丹东市元宝区)
文档属性
| 名称 | 一元三次函数(辽宁省丹东市元宝区) |

|
|
| 格式 | rar | ||
| 文件大小 | 49.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-08 00:00:00 | ||
图片预览



文档简介
一元三次函数性质与图象探索
高中部 宋润生
我们已经学习了一次函数,知道图象是单调递增或单调递减,在整个定义域上不存在最大值与最小值,在某一区间取得最大值与最小值.那么,是什么决定函数的单调性呢?利用已学过的知识得出:当k>0时函数单调递增;当k<0时函数单调递增;b决定函数与y轴相交的位置.
接着,我们同样学习了二次函数,图象大致如下:
图1 图2
利用已学知识归纳得出:当时(如图1),在对称轴的左侧单调递减、右侧单调递增,对称轴上取得最小值;当时(图2),在对称轴的左侧单调递增、右侧单调递减,对称轴上取得最大值.在某一区间取得最大值与最小值.其中a决定函数的开口方向,a、b同时决定对称轴,c决定函数与y轴相交的位置.
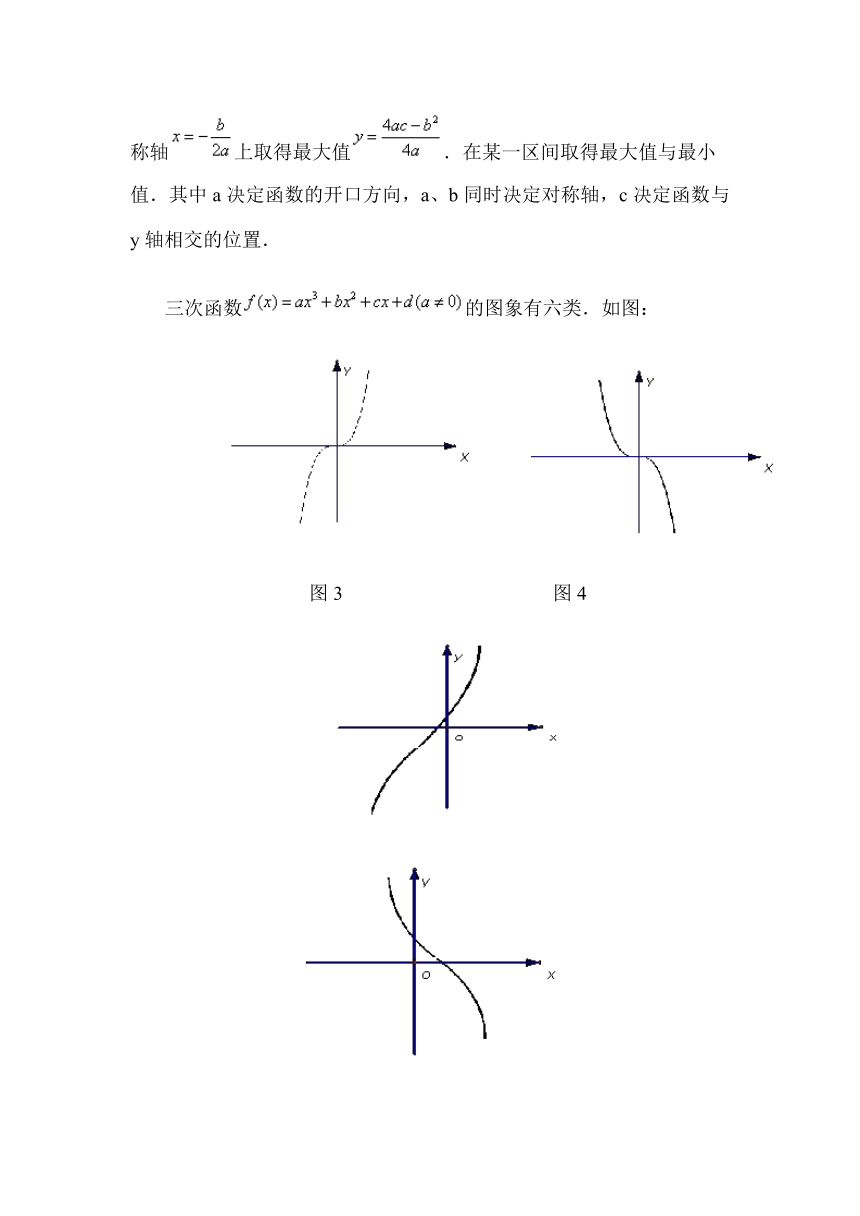
三次函数的图象有六类.如图:
图3 图4
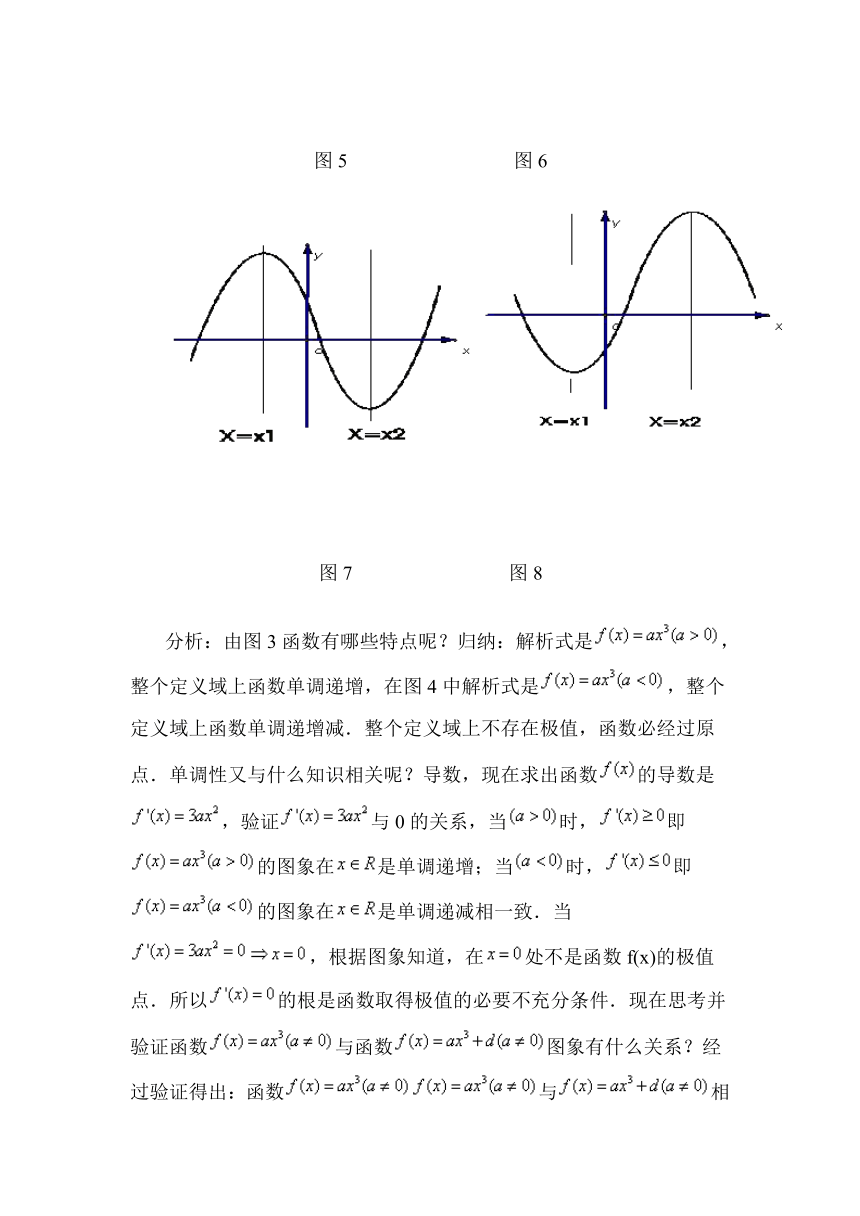
图5 图6
图7 图8
分析:由图3函数有哪些特点呢?归纳:解析式是,整个定义域上函数单调递增,在图4中解析式是,整个定义域上函数单调递增减.整个定义域上不存在极值,函数必经过原点.单调性又与什么知识相关呢?导数,现在求出函数的导数是,验证与0的关系,当时,即的图象在是单调递增;当时,即的图象在是单调递减相一致.当,根据图象知道,在处不是函数f(x)的极值点.所以的根是函数取得极值的必要不充分条件.现在思考并验证函数与函数图象有什么关系?经过验证得出:函数与相同,当时函数图象是图象向上平移|d|个单位;当时函数图象是图象向下平移|d|个单位;函数的导数都是.
在图5中解析式是,整个定义域上函数单调递增.在图6中解析式是,整个定义域上函数单调递增减.整个定义域上不存在极值.函数的导数,经过验证在图5中因为即,所以的图象在是单调递增;在图6中因为即,所以的图象在是单调递减;函数都不存在极大值或极小值.为什么在图5中a>0、,在图6中a<0、呢?a>0、或a<0、是又有什么结果呢?因为导数是二次函数,当a>0、或a<0、时判别式,导数函数不小于0,方程有一个根.当a>0、或a<0、时,方程有两个根.那么函数图象有什么特点呢?猜想如果,那么有两根,函数f(x)应有增也有减,我们来验证一下图7、图8:
在图7中解析式是,在或上函数单调递增,在上函数单调递减;在处取得极大值,在处取得极小值;在图8中解析式是,在或上函数单调递减,在上函数单调递增;在处取得极小值,在处取得极大值,它们在上最大值和最小值.为什么呢?函数的导数是,设的两根是并且令.经过验证在图7中,因为,当或时,所以的图象在或是单调递增;在上,所以的图象在是单调递减.在图8中,因为,当或时,所以的图象在或是单调递减;在上,所以的图象在是单调递增.
经过上述探索知道,函数在整个定义域上是单调递增(递减),左右都增中间递减,还是左右都减中间递增,是由a确定,b、c确定函数有没有极值、d确定函数与 y轴的交点.并且函数单调递增(递减)有没有极值与的导函数的判别式相关,具体归纳如下性质:
设的导数是则,函数的判别式为:由导数的图象可知:
时导数的图象 时导数图象
图9 图10
函数f(x)图象
图11 图12
三次函数f (x)在R上是单调函数,(无极值)
时的两根为且导数图象
图13
函数f (x)图象 函数f (x)图象
图14 图15
1、时在或单调递增;在单调递减(如图14)在处取得极大值,在处取得极小值.
2、时在或单调递减;在单调递增,(如图15)在处取得极小值,在处取得极大值.
注意:三次函数f(x)有极值导函数的判别式>0
三次函数图象的对称性:
三次函数的图象是中心对称图形,其对称中心是(-b/3a,f(-b/3a)).(三次函数的图象经过平移后能得到奇函数图象,可以用待定系数法求得)
三次函数的图象的对称中心在其导函数的图象对称轴上.
若三次函数有极值,那么它的对称中心是两个极值点的中点.
根据以上性质可以灵活解决三次函数问题:
例1、设,讨论关于x的方程的相异实根的个数?
解:分析:要讨论方程根的个数,直接求解非常困难,根据题意,需把方程转化为函数问题,即方程变成,设,这转化为讨论函数与交点的个数.
函数的导数的两根为(如图16)
函数的极大值是,函数的极小值是,
(1)当或时,函数与只有一个交点,即方程只有一个根.
(2)当或时,函数与只有两个交点,即方程只有两个根.
(3)当时,函数与有三个交点,方程有三个根.
图16
例2、已知函数是R上的奇函数,当时f(x)取得极值.
(1)求f(x)的单调区间和极大值;
(2)证明对任意,,不等式恒成立.
解:(1)函数f(x)是奇函数,所以,函数f(x)的导数依题意得,,解得
所以导数,(如图17)
时,函数f(x)单调递增;
时,函数f(x)单调递减;所以.
(2)如图17 对任意,, 函数f(x)单调递减,所以
图17
一般地在导数有两根且时,在处;在处,对任意都有
我们利用研究函数的性质的方法和导数知识能够轻松研究三次(高次)函数的性质,使学生既学到了新知识,又巩固了旧知识,充分利用好导数知识,能更有效解决三次函数的极值、对称性、证明不等式等问题找到较好的解决办法.
高中部 宋润生
我们已经学习了一次函数,知道图象是单调递增或单调递减,在整个定义域上不存在最大值与最小值,在某一区间取得最大值与最小值.那么,是什么决定函数的单调性呢?利用已学过的知识得出:当k>0时函数单调递增;当k<0时函数单调递增;b决定函数与y轴相交的位置.
接着,我们同样学习了二次函数,图象大致如下:
图1 图2
利用已学知识归纳得出:当时(如图1),在对称轴的左侧单调递减、右侧单调递增,对称轴上取得最小值;当时(图2),在对称轴的左侧单调递增、右侧单调递减,对称轴上取得最大值.在某一区间取得最大值与最小值.其中a决定函数的开口方向,a、b同时决定对称轴,c决定函数与y轴相交的位置.
三次函数的图象有六类.如图:
图3 图4
图5 图6
图7 图8
分析:由图3函数有哪些特点呢?归纳:解析式是,整个定义域上函数单调递增,在图4中解析式是,整个定义域上函数单调递增减.整个定义域上不存在极值,函数必经过原点.单调性又与什么知识相关呢?导数,现在求出函数的导数是,验证与0的关系,当时,即的图象在是单调递增;当时,即的图象在是单调递减相一致.当,根据图象知道,在处不是函数f(x)的极值点.所以的根是函数取得极值的必要不充分条件.现在思考并验证函数与函数图象有什么关系?经过验证得出:函数与相同,当时函数图象是图象向上平移|d|个单位;当时函数图象是图象向下平移|d|个单位;函数的导数都是.
在图5中解析式是,整个定义域上函数单调递增.在图6中解析式是,整个定义域上函数单调递增减.整个定义域上不存在极值.函数的导数,经过验证在图5中因为即,所以的图象在是单调递增;在图6中因为即,所以的图象在是单调递减;函数都不存在极大值或极小值.为什么在图5中a>0、,在图6中a<0、呢?a>0、或a<0、是又有什么结果呢?因为导数是二次函数,当a>0、或a<0、时判别式,导数函数不小于0,方程有一个根.当a>0、或a<0、时,方程有两个根.那么函数图象有什么特点呢?猜想如果,那么有两根,函数f(x)应有增也有减,我们来验证一下图7、图8:
在图7中解析式是,在或上函数单调递增,在上函数单调递减;在处取得极大值,在处取得极小值;在图8中解析式是,在或上函数单调递减,在上函数单调递增;在处取得极小值,在处取得极大值,它们在上最大值和最小值.为什么呢?函数的导数是,设的两根是并且令.经过验证在图7中,因为,当或时,所以的图象在或是单调递增;在上,所以的图象在是单调递减.在图8中,因为,当或时,所以的图象在或是单调递减;在上,所以的图象在是单调递增.
经过上述探索知道,函数在整个定义域上是单调递增(递减),左右都增中间递减,还是左右都减中间递增,是由a确定,b、c确定函数有没有极值、d确定函数与 y轴的交点.并且函数单调递增(递减)有没有极值与的导函数的判别式相关,具体归纳如下性质:
设的导数是则,函数的判别式为:由导数的图象可知:
时导数的图象 时导数图象
图9 图10
函数f(x)图象
图11 图12
三次函数f (x)在R上是单调函数,(无极值)
时的两根为且导数图象
图13
函数f (x)图象 函数f (x)图象
图14 图15
1、时在或单调递增;在单调递减(如图14)在处取得极大值,在处取得极小值.
2、时在或单调递减;在单调递增,(如图15)在处取得极小值,在处取得极大值.
注意:三次函数f(x)有极值导函数的判别式>0
三次函数图象的对称性:
三次函数的图象是中心对称图形,其对称中心是(-b/3a,f(-b/3a)).(三次函数的图象经过平移后能得到奇函数图象,可以用待定系数法求得)
三次函数的图象的对称中心在其导函数的图象对称轴上.
若三次函数有极值,那么它的对称中心是两个极值点的中点.
根据以上性质可以灵活解决三次函数问题:
例1、设,讨论关于x的方程的相异实根的个数?
解:分析:要讨论方程根的个数,直接求解非常困难,根据题意,需把方程转化为函数问题,即方程变成,设,这转化为讨论函数与交点的个数.
函数的导数的两根为(如图16)
函数的极大值是,函数的极小值是,
(1)当或时,函数与只有一个交点,即方程只有一个根.
(2)当或时,函数与只有两个交点,即方程只有两个根.
(3)当时,函数与有三个交点,方程有三个根.
图16
例2、已知函数是R上的奇函数,当时f(x)取得极值.
(1)求f(x)的单调区间和极大值;
(2)证明对任意,,不等式恒成立.
解:(1)函数f(x)是奇函数,所以,函数f(x)的导数依题意得,,解得
所以导数,(如图17)
时,函数f(x)单调递增;
时,函数f(x)单调递减;所以.
(2)如图17 对任意,, 函数f(x)单调递减,所以
图17
一般地在导数有两根且时,在处;在处,对任意都有
我们利用研究函数的性质的方法和导数知识能够轻松研究三次(高次)函数的性质,使学生既学到了新知识,又巩固了旧知识,充分利用好导数知识,能更有效解决三次函数的极值、对称性、证明不等式等问题找到较好的解决办法.
