思维拔高特训:多边形的面积-数学五年级上册苏教版(含解析)
文档属性
| 名称 | 思维拔高特训:多边形的面积-数学五年级上册苏教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
思维拔高特训:多边形的面积-数学五年级上册苏教版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级等信息
2.注意卷面整洁
一、选择题(共18分)
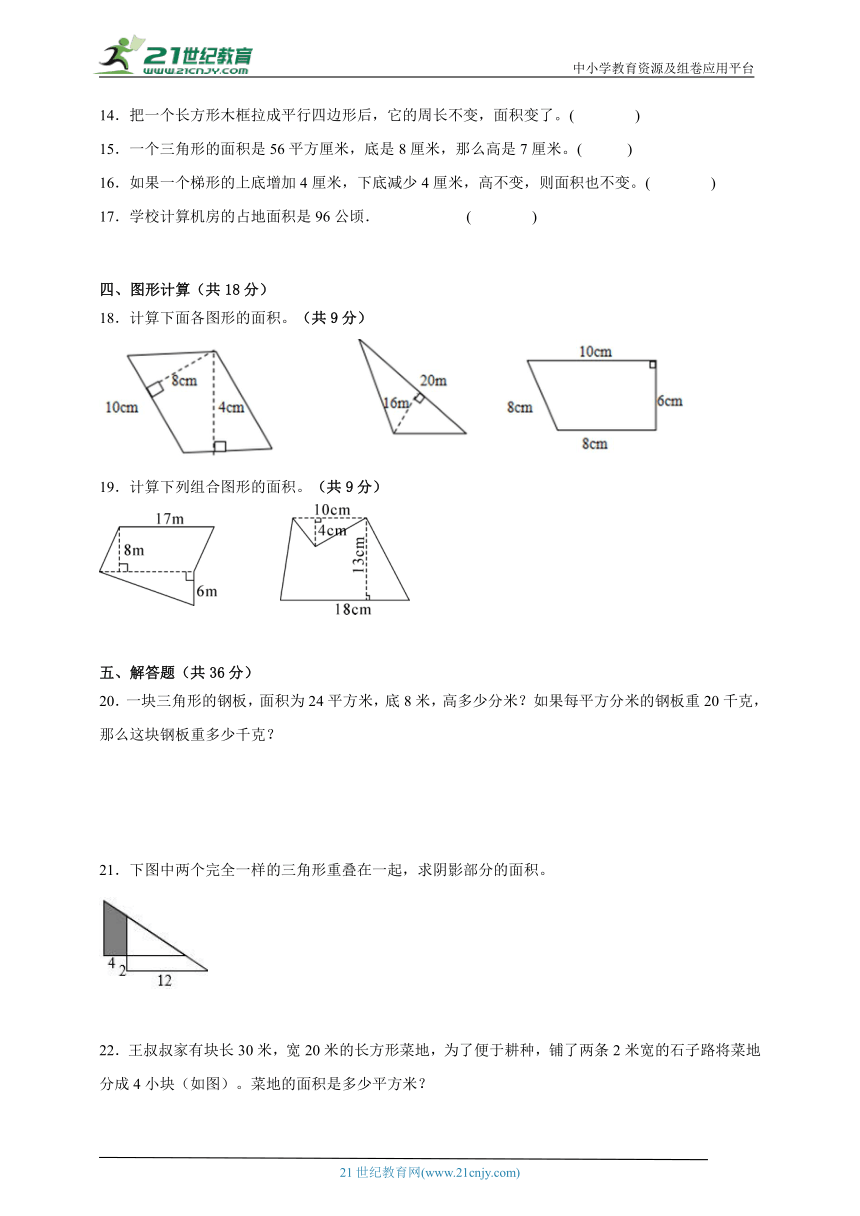
1.3个面积1平方分米的正方形拼成一个长方形,在长方形里画一个梯形(如图),这个梯形的面积是多少?( )
A.4平方分米 B.3平方分米 C.2平方分米
2.一个直角三角形的旗帜,三条边分别是6分米、8分米、10 分米,则这个三角形的面积是( )平方分米。
A.24 B.30 C.40
3.一个三角形的底不变,要使面积扩大到原来的3倍,高要扩大到原来的( )。
A.1.5倍 B.3倍 C.6倍
4.下图中( )三角形是左面平行四边形的一半.
A.甲 B.乙 C.丙
5.一块三角形地的面积是4公顷,它的底是100米,它的高是( )米.
A.40 B.60 C.800
6.在面积为42平方米的平行四边形内画一个最大的三角形,这个三角形的面积是( )平方米.
A.21 B.30 C.14
二、填空题(共18分)
7.下图每个小方格表示1平方厘米,估计一下,图中树叶的面积大约是( )平方厘米。
8.如图,一个三角形的底长是5厘米,如果底减少1厘米,则三角形的面积就减少2平方厘米,原来三角形的面积是( )平方厘米。
9.求出下面图形的面积算式是( )。
10.如图,A点是平行四边形一边上的中点,图中梯形的面积比三角形的面积大60平方厘米,梯形的面积是( )平方厘米。
11.下图中涂色部分的面积是6平方厘米,最小正方形的面积是( )平方厘米。
12.一个直角梯形的上、下的和是24厘米,两条腰分别是8厘米和5厘米,它的面积是( )平方厘米。
三、判断题(共10分)
13.一个梯形的上底是6米,下底是8米,面积是42平方米,它的高是6米.( )
14.把一个长方形木框拉成平行四边形后,它的周长不变,面积变了。( )
15.一个三角形的面积是56平方厘米,底是8厘米,那么高是7厘米。( )
16.如果一个梯形的上底增加4厘米,下底减少4厘米,高不变,则面积也不变。( )
17.学校计算机房的占地面积是96公顷. ( )
四、图形计算(共18分)
18.计算下面各图形的面积。(共9分)
19.计算下列组合图形的面积。(共9分)
五、解答题(共36分)
20.一块三角形的钢板,面积为24平方米,底8米,高多少分米?如果每平方分米的钢板重20千克,那么这块钢板重多少千克?
21.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
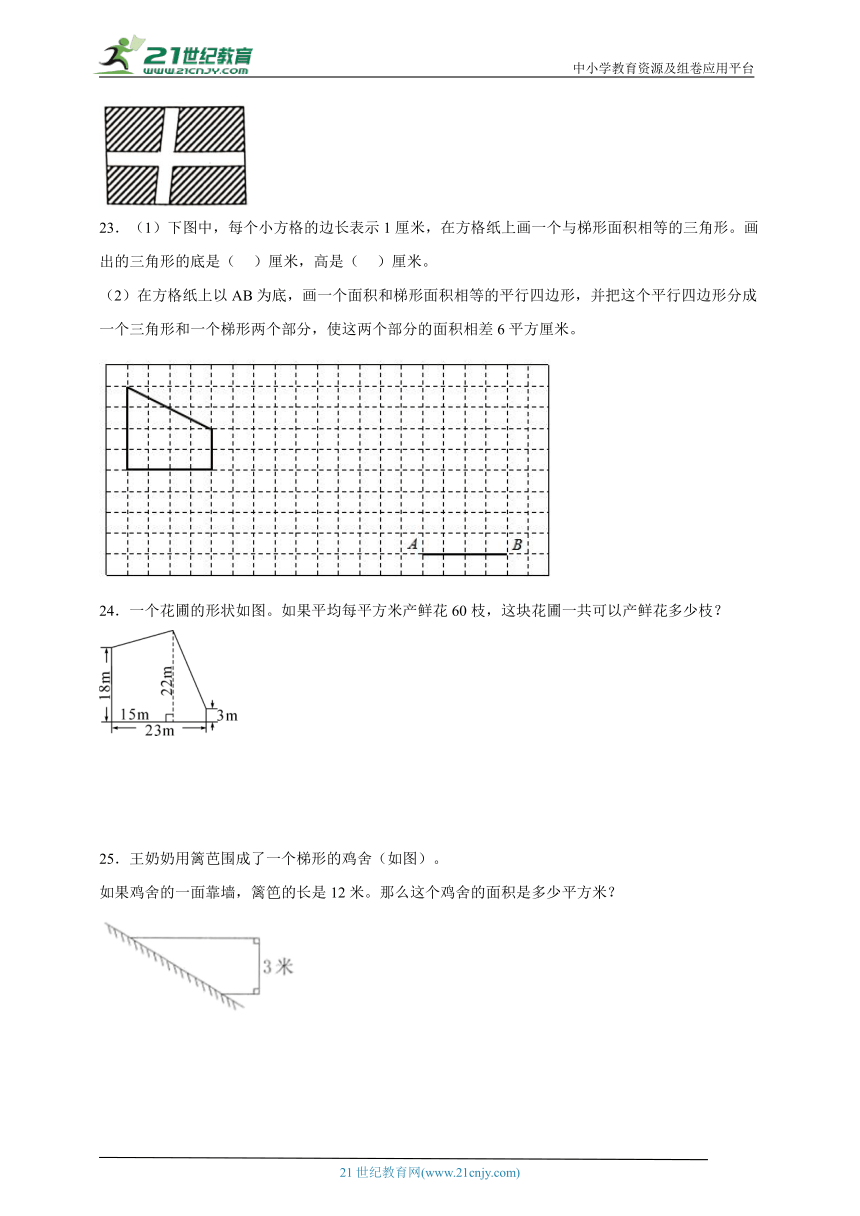
22.王叔叔家有块长30米,宽20米的长方形菜地,为了便于耕种,铺了两条2米宽的石子路将菜地分成4小块(如图)。菜地的面积是多少平方米?
23.(1)下图中,每个小方格的边长表示1厘米,在方格纸上画一个与梯形面积相等的三角形。画出的三角形的底是( )厘米,高是( )厘米。
(2)在方格纸上以AB为底,画一个面积和梯形面积相等的平行四边形,并把这个平行四边形分成一个三角形和一个梯形两个部分,使这两个部分的面积相差6平方厘米。
24.一个花圃的形状如图。如果平均每平方米产鲜花60枝,这块花圃一共可以产鲜花多少枝?
25.王奶奶用篱芭围成了一个梯形的鸡舍(如图)。
如果鸡舍的一面靠墙,篱笆的长是12米。那么这个鸡舍的面积是多少平方米?
参考答案:
1.C
【分析】面积是1平方分米的正方形的边长是1分米,所以梯形的上底是1分米,下底是3分米,高是1分米,代入梯形的面积公式即可解答问题。
【详解】面积是1平方分米的正方形的边长是1分米。
(1+3)×1÷2
=4×1÷2
=2(平方分米)
故答案为:C。
【点睛】此题考查梯形的面积=(上底+下底)×高÷2的计算应用。
2.A
【详解】略
3.B
【分析】三角形的面积公式:S=ah÷2,根据积的变化规律知:一个因数不变,另一个因数扩大到原来的几倍或缩小到原来的几分之几,积也扩大到原来的几倍或缩小到原来的几分之几,据此解答。
【详解】由分析可得:三角形的面积扩大3倍,底不变,高要扩大3倍。
故答案为:B
【点睛】本题主要考查了学生根据积的变化规律和三角形的面积公式来解答问题的能力。
4.A
【分析】三角形面积=底×高÷2,平行四边形面积=底×高,所以等底等高的三角形面积是平行四边形面积的一半.
【详解】甲和平行四边形等底等高,所以甲三角形是左面平行四边形的一半.
故答案为A
5.C
【详解】略
6.A
【详解】略
7.9
【分析】用数方格的方法估计树叶的面积。先数整格的,再数不满整格的,不满整格的按半格计算,最后把两者加起来。
【详解】不满整格的有10个,相当于10÷2=5个整格;整格的有4个。
5+4=9(个)
9×1=9(平方厘米)
【点睛】用数方格的方法估计不规则图形的面积,一般把不满整格的按半格计算。
8.10
【分析】由图可知,减少的三角形的面积与原来的三角形等高,根据三角形的高=面积×2÷底,求出减少部分三角形的高,也就是原来三角形的高,再根据三角形的面积=底×高÷2,代入数据计算即可。
【详解】2×2÷1=4(厘米)
5×4÷2
=20÷2
=10(平方厘米)
原来三角形的面积是10平方厘米。
【点睛】此题考查了三角形面积的相关计算,需牢记公式并能灵活运用。
9.12×4+(12+15)×(10-4)÷2
【分析】
如上图,添加辅助线后,图形被分成一个长为12米,宽为4米的长方形和一个上底是12米,下底是15米,高为10-4=6米的梯形,再利用长方形和梯形面积公式列出长方形和梯形的面积后再相加,本题即可得解。
【详解】长方形面积算式:12×4
梯形面积算式:(12+15)×(10-4)÷2
总面积算式:12×4+(12+15)×(10-4)÷2
【点睛】把不规则图形分成常见的长方形和梯形是解答本题的关键。
10.90
【分析】由于A点是平行四边形上的中点,则三角形的底是平行四边形底边的一半,根据三角形的面积公式:底×高÷2,三角形的高是平行四边形的高,梯形的上底等于三角形的底,梯形的下底等于三角形底的2倍,根据梯形的面积公式:(上底+下底)×高÷2,梯形的高是平行四边形的高,由此即可知道梯形的面积=(三角形的底+2×三角形的底)×高÷2=3×三角形的底×高÷2,由此即可知道梯形的面积是三角形的3倍,由于梯形的面积比三角形的面积大60,则相当于2倍的三角形的面积是60,则三角形的面积:60÷2=30(平方厘米),梯形的面积:30×3=90平方厘米。
【详解】由分析可知,梯形的面积=3倍的三角形的面积
60÷(3-1)
=60÷2
=30(平方厘米)
30×3=90(平方厘米)
【点睛】本题主要考查三角形和梯形的面积公式,熟练掌握它们的面积公式并灵活运用。
11.24
【分析】作最小正方形的对角线,把中间的正方形平均分成8份,每份是6平方厘米,小正方形的面积是4份,用乘法即可求出最小正方形的面积。
【详解】作最小正方形的对角线,如图:
6×4=24(平方厘米)
【点睛】解题的关键是作最小正方形的对角线,进而解决问题。
12.60
【分析】由题意知:直角梯形中两条腰分别是8厘米和5厘米,可以判定5厘米是梯形的高。再根据梯形面积公式:梯形面积等于(上底+下底)×5÷2,据此解答。
【详解】24×5÷2
=120÷2
=60(平方厘米)
【点睛】掌握梯形的面积公式是解答本题的关键。本题的高没有直接送出,可注意辨别。
13.√
【解析】略
14.√
【分析】把长方形木框拉成平行四边形,四个边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了;据此解答。
【详解】由分析可知,把一个长方形木框拉成平行四边形后,它的周长不变,面积变了。
故答案为:√
【点睛】此题主要考查平行四边形的特征及性质。
15.×
【分析】根据三角形的面积公式,S=ah,将此公式变形为:h=2s÷a,求出高即可判断。
【详解】56×2÷8
=112÷8
=14(厘米)
答:三角形的高是14厘米。
故答案为:×。
【点睛】此题主要考查三角形的面积公式及其变式。
16.√
【分析】根据梯形的面积公式:s=(a+b)×h÷2,一个梯形,如果高不变,上底增加4厘米,下底减少4厘米,上下底之和没有变,所以面积不变。
【详解】根据分析知:一个梯形,如果高不变,上底增加4厘米,下底减少4厘米,上下底之和没有变,所以面积不变。
故答案为:√
【点睛】本题主要考查理解掌握梯形的面积公式,根据梯形的面积公式进行解答。
17.×
【解析】略
18.80 cm2;160m2;54 cm2
【分析】将数据带入平行四边形、三角形、梯形的面积公式计算即可。
【详解】10×8=80(cm2)
20×16÷2
=320÷2
=160(m2)
(10+8)×6÷2
=18×6÷2
=108÷2
=54(cm2)
19.187m2;162cm2
【分析】平行四边形的面积+三角形的面积即为第一个组合图形的面积;
梯形的面积-三角形的面积即为第二个组合图形的面积。
【详解】8×17+6×17÷2
=136+51
=187(m2)
(10+18)×13÷2-10×4÷2
=182-20
=162(cm2)
20.60分米;48000千克
【分析】已知三角形面积、底,求高,根据三角形面积公式:底×高÷2,代入数据,求出三角形的高;再用三角形的面积×20,即可求出这块钢板的重量。
【详解】24平方米=2400平方分米,8米=80分米
2400×2÷80
=4800÷80
=60(分米)
2400×20=48000(千克)
答:高是60分米;这块钢板重48000千克。
【点睛】本题考查三角形面积公式的应用,熟记公式,灵活运用,注意单位名数的统一。
21.20
【分析】两个三角形面积一样,扣掉中间重叠部分三角形,剩下面积一样,所以阴影部分面积等于梯形面积。
【详解】[(12-4)+12]×2÷2
=20×2÷2
=20
【点睛】解答此题的关键是能够把所求阴影部分的面积转化成求梯形的面积。
22.504平方米
【分析】由题意可知:可以将菜地向中间“挤压”,把“小路挤掉”,则剩下的就是菜地的面积,其长和宽分别为(30-2)米和(20-2)米,利用长方形的面积公式S=ab,求出其面积。
【详解】由分析可得,菜地的面积为:
(30-2)×(20-2)
=28×18
=504(平方米)
答:菜地的面积是504平方米。
【点睛】此题考查了长方形面积公式的实际运用,解答此题的关键是:利用“压缩法”,把“小路挤掉”,求新长方形的面积即为菜地的面积。
23.(1)见详解;
(2)见详解
【分析】(1)根据图意先计算出梯形的面积,所画的三角形的面积和梯形的面积相等,于是可以确定三角形的底和高,进而就可以在方格图中画出三角形。
(2)由图意可知,梯形的面积是12平方厘米,所画的平行四边形的底已知是4cm,则高是12÷4=3(cm),进而就可以在方格图中画出平行四边形,把这个平行四边形分成一个三角形和一个梯形两个部分,使这两个部分的面积相差6平方厘米,用和差公式求出三角形的面积和梯形的面积各是多少,再根据图形划线分开。
【详解】(1)梯形的面积:
(2+4)×4÷2
=6×4÷2
=12(平方厘米)
12×2=24,即所画的三角形的底和高的积是24,4×6=24,所画的三角形的底可以是6厘米,高是4厘米。如下图所示:
(2)梯形的面积是12平方厘米,则所画的平行四边形的面积也是12平方厘米,已知底是4厘米,则高为:12÷4=3(厘米);
所分的三角形的面积:(12-6)÷2=3(平方厘米),已知三角形的高是3厘米,则底应是3×2÷3=2(厘米),作图如下:
【点睛】此题主要考查三角形、平行四边形和梯形的面积的计算方法的灵活应用,关键是先确定出计算这几个图形的面积所需要的主要线段的长度,进而完成画图。
24.24000枝
【分析】根据梯形的面积=(上底+下底)×高÷2分别求出2个梯形的面积,两者相加即为这个花圃的面积,再乘60即为这块花圃一共可以产鲜花的数量。
【详解】(18+22)×15÷2
=40×15÷2
=300(平方米)
23-15=8(米)
(3+22)×8÷2
=25×8÷2
=100(平方米)
300+100=400(平方米)
400×60=24000(枝)
答:这块花圃一共可以产鲜花24000枝。
【点睛】解答此题的关键是把这个多边形的面积转化为2个梯形面积的和。
25.13.5平方米
【分析】根据题意,用篱笆的长度减去3米即是梯形的上底、下底之和。根据梯形面积=(上底+下底)×高÷2即可解答。
【详解】(12-3)×3÷2
=9×3÷2
=13.5(平方米)
答:这个鸡舍的面积是13.5平方米。
【点睛】理解篱笆的长度减去3米即是梯形的上底、下底之和是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拔高特训:多边形的面积-数学五年级上册苏教版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级等信息
2.注意卷面整洁
一、选择题(共18分)
1.3个面积1平方分米的正方形拼成一个长方形,在长方形里画一个梯形(如图),这个梯形的面积是多少?( )
A.4平方分米 B.3平方分米 C.2平方分米
2.一个直角三角形的旗帜,三条边分别是6分米、8分米、10 分米,则这个三角形的面积是( )平方分米。
A.24 B.30 C.40
3.一个三角形的底不变,要使面积扩大到原来的3倍,高要扩大到原来的( )。
A.1.5倍 B.3倍 C.6倍
4.下图中( )三角形是左面平行四边形的一半.
A.甲 B.乙 C.丙
5.一块三角形地的面积是4公顷,它的底是100米,它的高是( )米.
A.40 B.60 C.800
6.在面积为42平方米的平行四边形内画一个最大的三角形,这个三角形的面积是( )平方米.
A.21 B.30 C.14
二、填空题(共18分)
7.下图每个小方格表示1平方厘米,估计一下,图中树叶的面积大约是( )平方厘米。
8.如图,一个三角形的底长是5厘米,如果底减少1厘米,则三角形的面积就减少2平方厘米,原来三角形的面积是( )平方厘米。
9.求出下面图形的面积算式是( )。
10.如图,A点是平行四边形一边上的中点,图中梯形的面积比三角形的面积大60平方厘米,梯形的面积是( )平方厘米。
11.下图中涂色部分的面积是6平方厘米,最小正方形的面积是( )平方厘米。
12.一个直角梯形的上、下的和是24厘米,两条腰分别是8厘米和5厘米,它的面积是( )平方厘米。
三、判断题(共10分)
13.一个梯形的上底是6米,下底是8米,面积是42平方米,它的高是6米.( )
14.把一个长方形木框拉成平行四边形后,它的周长不变,面积变了。( )
15.一个三角形的面积是56平方厘米,底是8厘米,那么高是7厘米。( )
16.如果一个梯形的上底增加4厘米,下底减少4厘米,高不变,则面积也不变。( )
17.学校计算机房的占地面积是96公顷. ( )
四、图形计算(共18分)
18.计算下面各图形的面积。(共9分)
19.计算下列组合图形的面积。(共9分)
五、解答题(共36分)
20.一块三角形的钢板,面积为24平方米,底8米,高多少分米?如果每平方分米的钢板重20千克,那么这块钢板重多少千克?
21.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
22.王叔叔家有块长30米,宽20米的长方形菜地,为了便于耕种,铺了两条2米宽的石子路将菜地分成4小块(如图)。菜地的面积是多少平方米?
23.(1)下图中,每个小方格的边长表示1厘米,在方格纸上画一个与梯形面积相等的三角形。画出的三角形的底是( )厘米,高是( )厘米。
(2)在方格纸上以AB为底,画一个面积和梯形面积相等的平行四边形,并把这个平行四边形分成一个三角形和一个梯形两个部分,使这两个部分的面积相差6平方厘米。
24.一个花圃的形状如图。如果平均每平方米产鲜花60枝,这块花圃一共可以产鲜花多少枝?
25.王奶奶用篱芭围成了一个梯形的鸡舍(如图)。
如果鸡舍的一面靠墙,篱笆的长是12米。那么这个鸡舍的面积是多少平方米?
参考答案:
1.C
【分析】面积是1平方分米的正方形的边长是1分米,所以梯形的上底是1分米,下底是3分米,高是1分米,代入梯形的面积公式即可解答问题。
【详解】面积是1平方分米的正方形的边长是1分米。
(1+3)×1÷2
=4×1÷2
=2(平方分米)
故答案为:C。
【点睛】此题考查梯形的面积=(上底+下底)×高÷2的计算应用。
2.A
【详解】略
3.B
【分析】三角形的面积公式:S=ah÷2,根据积的变化规律知:一个因数不变,另一个因数扩大到原来的几倍或缩小到原来的几分之几,积也扩大到原来的几倍或缩小到原来的几分之几,据此解答。
【详解】由分析可得:三角形的面积扩大3倍,底不变,高要扩大3倍。
故答案为:B
【点睛】本题主要考查了学生根据积的变化规律和三角形的面积公式来解答问题的能力。
4.A
【分析】三角形面积=底×高÷2,平行四边形面积=底×高,所以等底等高的三角形面积是平行四边形面积的一半.
【详解】甲和平行四边形等底等高,所以甲三角形是左面平行四边形的一半.
故答案为A
5.C
【详解】略
6.A
【详解】略
7.9
【分析】用数方格的方法估计树叶的面积。先数整格的,再数不满整格的,不满整格的按半格计算,最后把两者加起来。
【详解】不满整格的有10个,相当于10÷2=5个整格;整格的有4个。
5+4=9(个)
9×1=9(平方厘米)
【点睛】用数方格的方法估计不规则图形的面积,一般把不满整格的按半格计算。
8.10
【分析】由图可知,减少的三角形的面积与原来的三角形等高,根据三角形的高=面积×2÷底,求出减少部分三角形的高,也就是原来三角形的高,再根据三角形的面积=底×高÷2,代入数据计算即可。
【详解】2×2÷1=4(厘米)
5×4÷2
=20÷2
=10(平方厘米)
原来三角形的面积是10平方厘米。
【点睛】此题考查了三角形面积的相关计算,需牢记公式并能灵活运用。
9.12×4+(12+15)×(10-4)÷2
【分析】
如上图,添加辅助线后,图形被分成一个长为12米,宽为4米的长方形和一个上底是12米,下底是15米,高为10-4=6米的梯形,再利用长方形和梯形面积公式列出长方形和梯形的面积后再相加,本题即可得解。
【详解】长方形面积算式:12×4
梯形面积算式:(12+15)×(10-4)÷2
总面积算式:12×4+(12+15)×(10-4)÷2
【点睛】把不规则图形分成常见的长方形和梯形是解答本题的关键。
10.90
【分析】由于A点是平行四边形上的中点,则三角形的底是平行四边形底边的一半,根据三角形的面积公式:底×高÷2,三角形的高是平行四边形的高,梯形的上底等于三角形的底,梯形的下底等于三角形底的2倍,根据梯形的面积公式:(上底+下底)×高÷2,梯形的高是平行四边形的高,由此即可知道梯形的面积=(三角形的底+2×三角形的底)×高÷2=3×三角形的底×高÷2,由此即可知道梯形的面积是三角形的3倍,由于梯形的面积比三角形的面积大60,则相当于2倍的三角形的面积是60,则三角形的面积:60÷2=30(平方厘米),梯形的面积:30×3=90平方厘米。
【详解】由分析可知,梯形的面积=3倍的三角形的面积
60÷(3-1)
=60÷2
=30(平方厘米)
30×3=90(平方厘米)
【点睛】本题主要考查三角形和梯形的面积公式,熟练掌握它们的面积公式并灵活运用。
11.24
【分析】作最小正方形的对角线,把中间的正方形平均分成8份,每份是6平方厘米,小正方形的面积是4份,用乘法即可求出最小正方形的面积。
【详解】作最小正方形的对角线,如图:
6×4=24(平方厘米)
【点睛】解题的关键是作最小正方形的对角线,进而解决问题。
12.60
【分析】由题意知:直角梯形中两条腰分别是8厘米和5厘米,可以判定5厘米是梯形的高。再根据梯形面积公式:梯形面积等于(上底+下底)×5÷2,据此解答。
【详解】24×5÷2
=120÷2
=60(平方厘米)
【点睛】掌握梯形的面积公式是解答本题的关键。本题的高没有直接送出,可注意辨别。
13.√
【解析】略
14.√
【分析】把长方形木框拉成平行四边形,四个边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了;据此解答。
【详解】由分析可知,把一个长方形木框拉成平行四边形后,它的周长不变,面积变了。
故答案为:√
【点睛】此题主要考查平行四边形的特征及性质。
15.×
【分析】根据三角形的面积公式,S=ah,将此公式变形为:h=2s÷a,求出高即可判断。
【详解】56×2÷8
=112÷8
=14(厘米)
答:三角形的高是14厘米。
故答案为:×。
【点睛】此题主要考查三角形的面积公式及其变式。
16.√
【分析】根据梯形的面积公式:s=(a+b)×h÷2,一个梯形,如果高不变,上底增加4厘米,下底减少4厘米,上下底之和没有变,所以面积不变。
【详解】根据分析知:一个梯形,如果高不变,上底增加4厘米,下底减少4厘米,上下底之和没有变,所以面积不变。
故答案为:√
【点睛】本题主要考查理解掌握梯形的面积公式,根据梯形的面积公式进行解答。
17.×
【解析】略
18.80 cm2;160m2;54 cm2
【分析】将数据带入平行四边形、三角形、梯形的面积公式计算即可。
【详解】10×8=80(cm2)
20×16÷2
=320÷2
=160(m2)
(10+8)×6÷2
=18×6÷2
=108÷2
=54(cm2)
19.187m2;162cm2
【分析】平行四边形的面积+三角形的面积即为第一个组合图形的面积;
梯形的面积-三角形的面积即为第二个组合图形的面积。
【详解】8×17+6×17÷2
=136+51
=187(m2)
(10+18)×13÷2-10×4÷2
=182-20
=162(cm2)
20.60分米;48000千克
【分析】已知三角形面积、底,求高,根据三角形面积公式:底×高÷2,代入数据,求出三角形的高;再用三角形的面积×20,即可求出这块钢板的重量。
【详解】24平方米=2400平方分米,8米=80分米
2400×2÷80
=4800÷80
=60(分米)
2400×20=48000(千克)
答:高是60分米;这块钢板重48000千克。
【点睛】本题考查三角形面积公式的应用,熟记公式,灵活运用,注意单位名数的统一。
21.20
【分析】两个三角形面积一样,扣掉中间重叠部分三角形,剩下面积一样,所以阴影部分面积等于梯形面积。
【详解】[(12-4)+12]×2÷2
=20×2÷2
=20
【点睛】解答此题的关键是能够把所求阴影部分的面积转化成求梯形的面积。
22.504平方米
【分析】由题意可知:可以将菜地向中间“挤压”,把“小路挤掉”,则剩下的就是菜地的面积,其长和宽分别为(30-2)米和(20-2)米,利用长方形的面积公式S=ab,求出其面积。
【详解】由分析可得,菜地的面积为:
(30-2)×(20-2)
=28×18
=504(平方米)
答:菜地的面积是504平方米。
【点睛】此题考查了长方形面积公式的实际运用,解答此题的关键是:利用“压缩法”,把“小路挤掉”,求新长方形的面积即为菜地的面积。
23.(1)见详解;
(2)见详解
【分析】(1)根据图意先计算出梯形的面积,所画的三角形的面积和梯形的面积相等,于是可以确定三角形的底和高,进而就可以在方格图中画出三角形。
(2)由图意可知,梯形的面积是12平方厘米,所画的平行四边形的底已知是4cm,则高是12÷4=3(cm),进而就可以在方格图中画出平行四边形,把这个平行四边形分成一个三角形和一个梯形两个部分,使这两个部分的面积相差6平方厘米,用和差公式求出三角形的面积和梯形的面积各是多少,再根据图形划线分开。
【详解】(1)梯形的面积:
(2+4)×4÷2
=6×4÷2
=12(平方厘米)
12×2=24,即所画的三角形的底和高的积是24,4×6=24,所画的三角形的底可以是6厘米,高是4厘米。如下图所示:
(2)梯形的面积是12平方厘米,则所画的平行四边形的面积也是12平方厘米,已知底是4厘米,则高为:12÷4=3(厘米);
所分的三角形的面积:(12-6)÷2=3(平方厘米),已知三角形的高是3厘米,则底应是3×2÷3=2(厘米),作图如下:
【点睛】此题主要考查三角形、平行四边形和梯形的面积的计算方法的灵活应用,关键是先确定出计算这几个图形的面积所需要的主要线段的长度,进而完成画图。
24.24000枝
【分析】根据梯形的面积=(上底+下底)×高÷2分别求出2个梯形的面积,两者相加即为这个花圃的面积,再乘60即为这块花圃一共可以产鲜花的数量。
【详解】(18+22)×15÷2
=40×15÷2
=300(平方米)
23-15=8(米)
(3+22)×8÷2
=25×8÷2
=100(平方米)
300+100=400(平方米)
400×60=24000(枝)
答:这块花圃一共可以产鲜花24000枝。
【点睛】解答此题的关键是把这个多边形的面积转化为2个梯形面积的和。
25.13.5平方米
【分析】根据题意,用篱笆的长度减去3米即是梯形的上底、下底之和。根据梯形面积=(上底+下底)×高÷2即可解答。
【详解】(12-3)×3÷2
=9×3÷2
=13.5(平方米)
答:这个鸡舍的面积是13.5平方米。
【点睛】理解篱笆的长度减去3米即是梯形的上底、下底之和是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
