华师大版八年级数学上册第13章全等三角形 单元测试题(含解析)
文档属性
| 名称 | 华师大版八年级数学上册第13章全等三角形 单元测试题(含解析) | 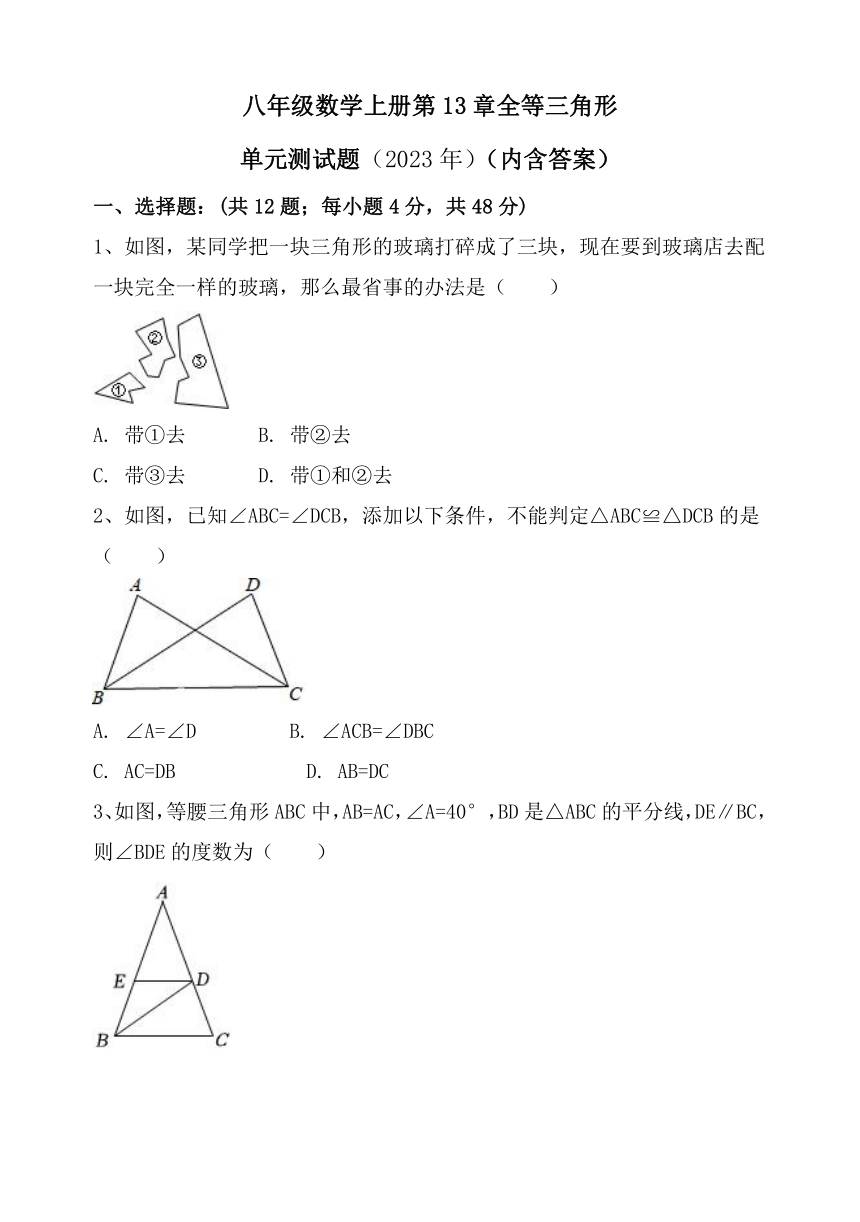 | |
| 格式 | docx | ||
| 文件大小 | 164.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 13:25:25 | ||
图片预览




文档简介
八年级数学上册第13章全等三角形
单元测试题(2023年)(内含答案)
一、选择题:(共12题;每小题4分,共48分)
1、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A. 带①去 B. 带②去
C. 带③去 D. 带①和②去
2、如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A. ∠A=∠D B. ∠ACB=∠DBC
C. AC=DB D. AB=DC
3、如图,等腰三角形ABC中,AB=AC,∠A=40°,BD是△ABC的平分线,DE∥BC,则∠BDE的度数为( )
A. 20° B. 35° C. 40° D. 70°
4、到三角形三个顶点的距离都相等的点是( )
A. 两条中线的交点 B. 两条高的交点
C. 两条角平线的交点 D. 两条边的垂直平分线的交点
5、已知等腰中,,则的度数为( )
A. B.
C. 或 D. 或或
如图,在等腰三角形ABC中,AD是底边BC上的中线,DE是△ABD高线.图中与∠BAD一定相等的角有(不含本身)( )
A. 1个 B. 2个 C. 3个 D. 4个
7、如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.若∠B=75°,∠AFB=40°,则∠D的度数为( )
A. 60° B. 65° C. 70° D. 75°
8、在△ABC和△DEF中,已知AB=DE,∠A=∠D,下列条件:①AC=DF;②∠B=∠E;③∠C=∠F;④BC=EF.其中一定能判定△ABC≌△DEF的个数为( )
A. 1 B. 2 C. 3 D. 4
9、如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A. ∠B=∠E B. BC∥EF C. ∠BCA=∠F D. ∠A=∠EDF
10、在△ABC中,∠B=90°,CD平分∠ACB,DE⊥AC于点E,若AB=4cm,则AD+DE的值为( )
A. 3cm B. 4cm C. 5cm D. 6cm
11、在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是( )
A. 0<AD<12 B. 1<AD<6 C. 0<AD<6 D. 2<AD<12
12、如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接FG;下列结论:①AE=BD;②AG=BF;③△BCF≌△DCF;④∠BOE=120°.其中正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
二、填空题:(共6题;每小题4分,共24分)
13、如果等腰三角形的两条边的比是1:2,周长是40cm,那么这等腰三角形底边上的高是_____cm.
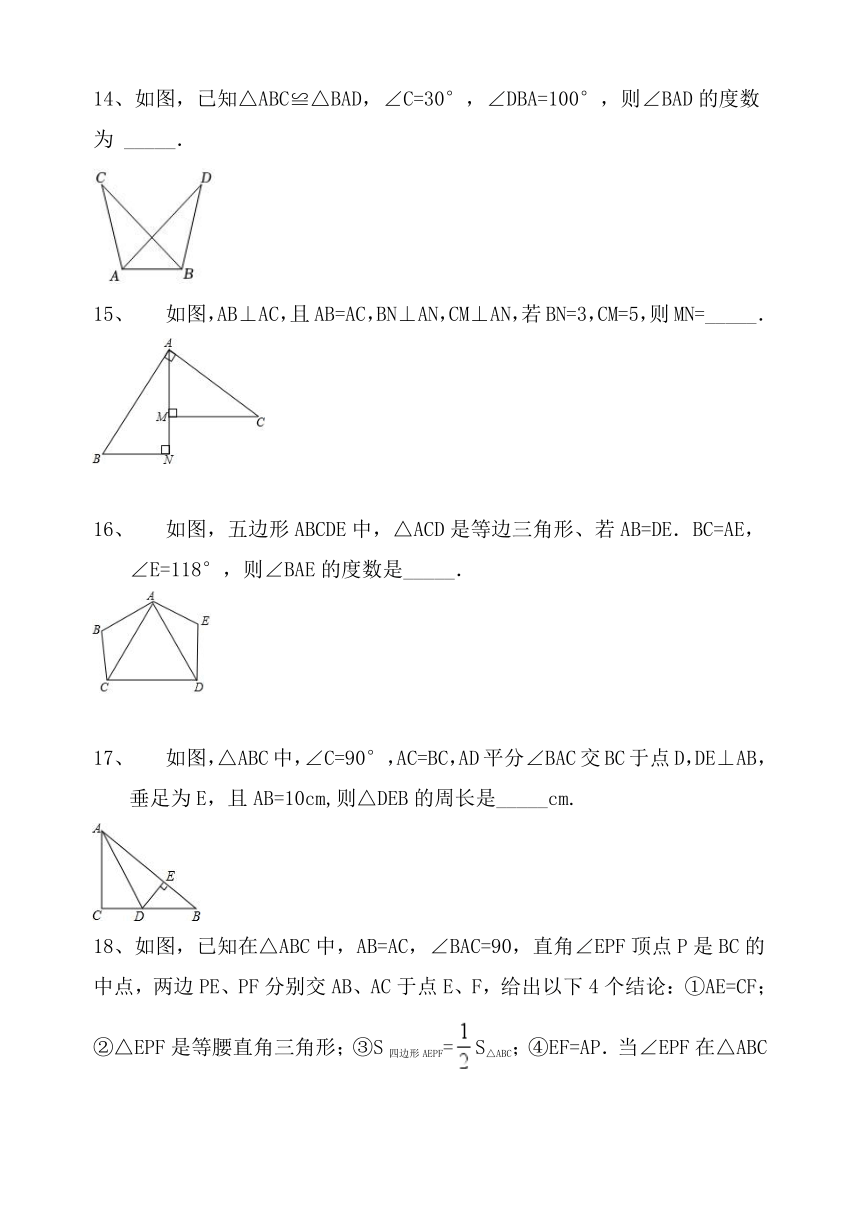
14、如图,已知△ABC≌△BAD,∠C=30°,∠DBA=100°,则∠BAD的度数为 _____.
如图,AB⊥AC,且AB=AC,BN⊥AN,CM⊥AN,若BN=3,CM=5,则MN=_____.
如图,五边形ABCDE中,△ACD是等边三角形、若AB=DE.BC=AE,∠E=118°,则∠BAE的度数是_____.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长是_____cm.
18、如图,已知在△ABC中,AB=AC,∠BAC=90,直角∠EPF顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下4个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内部绕顶点P旋转时(点E不与AB重合),上述结论始终成立的是________.
三、解答题:(共8题;共78分)
19、(8分)如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
20、(8分)如图,已知AB=AD,AC=AE,∠1=∠2
求证:∠B=∠D.
21、(10分)如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
求证:∠CEA=∠DEA.
22、(10分)如图,已知AB∥CD,AE∥CF,BF=DE
求证:AB=CD.
23、(10分)已知:如图AC、BD相交于点O,AC=BD,BC=AD,求证:OC=OD.
24、(10分)如图,BD平分∠ADC,∠A=∠B=90°,OA=OB.求证:CA平分∠DCB.
25、(10分)如图,已知点B、D、E、C在同一直线上,∠ADE=∠AED,BD=CE.
求证:AB=AC.
26、(12分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于F,
求证:(1)BE平分∠ABC
(2)AB=BC+AD
试卷答案
选择题
1、【答案】C
【解析】此题可以采用全等三角形的判定方法以及排除法进行分析,从而确定最后的答案.
解:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误;
B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误;
C、带③去,不但保留了原三角形的两个角还保留了其中一条边,符合ASA判定,故C选项正确;
D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D选项错误.
故选:C.
2、【答案】C
【解析】全等三角形的判定方法有SAS,ASA,AAS,SSS,根据定理逐个判断即可.
解:A、∠A=∠D,∠ABC=∠DCB,BC=BC,符合AAS,即能推出△ABC≌△DCB,故本选项错误;
B、∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合ASA,即能推出△ABC≌△DCB,故本选项错误;
C、∠ABC=∠DCB,AC=BD,BC=BC,不符合全等三角形的判定定理,即不能推出△ABC≌△DCB,故本选项正确;
D、AB=DC,∠ABC=∠DCB,BC=BC,符合SAS,即能推出△ABC≌△DCB,故本选项错误;
故选:C.
3、【答案】B
【解析】根据等腰三角形的性质推出∠ABC=70°,根据角平分线的定义得出∠DBC=35°,根据平行线的性质即可得解.
解:∵AB=AC,
∴∠ABC=∠C,
∵∠A=40°,
∴∠ABC=×(180°-40°)=70°,
∵BD是△ABC的平分线,
∴∠DBC=∠ABC=35°,
∵DE∥BC,
∴∠BDE=∠DBC=35°,
故选:B.
4、【答案】D
【解析】根据线段垂直分线的性质解答即可.
解:∵线段垂直平分线上任意一点,到线段两端点的距离相等,
∴到三角形三个顶点的距离都相等的点是两条边的垂直平分线的交点.
故选:D.
5、【答案】D
【解析】此题分为:为顶角、为顶角和、同为底角,再根据三角形内角和定理,等腰三角形的性质求得的度数.
解:当为顶角时,则;
当为顶角时,则;
当、为底角时,则.
故选:D.
【点睛】本题主要考查等腰三角形的性质,掌握等腰三角形的两底角相等是解题的关键,注意分类讨论.
6、【答案】B
【解析】由三线合一得∠DAC=∠BAD,再由直角三角形两个锐角互余得∠BAD=∠BDE.
解:∵△ABC为等腰三角形,AD是底边BC上的中线,
∴AD平分∠BAC,
∴∠DAC=∠BAD,
∵∠BAD+∠ADE=∠BDE+∠ADE=90°,
∴∠BAD=∠BDE,
∴∠BAD=∠BDE=∠DAC,
所以有2个角和它相等,
故选:B.
7、【答案】B
【解析】由BE=CF推导出BF=CE,即可根据全等三角形的判定定理“SAS”证明△ABF≌△DCE,则∠A=∠D=180°-75°-40°=65°,
解:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS),
∵∠B=75°,∠AFB=40°,
∴∠A=∠D=180°-∠B-∠AFB=180°-75°-40°=65°,
∴∠D的度数为65°,
故选:B.
8、【答案】C
【解析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理逐个判断即可.
解:如图,
①∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
故①正确;
②∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
故②正确;
③∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
故③正确;
④根据AB=DE,BC=EF,∠A=∠D不能推出△ABC≌△DEF,
∴④错误;
故选:C.
9、【答案】A
【解析】等三角形的判定方法SAS是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可.
解:∵AB=DE,BC=EF,
∴要使△ABC≌△DEF,
只要满足∠B=∠E或AC=BC即可,
故选:A.
10、【答案】B
【解析】先根据角平分线的性质得出BD=DE,进而可得出结论.
解:∵在△ABC中,∠B=90°,CD平分∠ACB,DE⊥AC于点E,
∴DE=BD.
∵AB=4cm,
∴AD+DE=AD+BD=AB=4cm.
故选:B.
11、【答案】B
【解析】作出图形,延长中线AD到E,使DE=AD,利用“边角边”证明△ACD和△EBD全等,根据全等三角形对应边相等可得AC=BE,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE的范围,再除以2即可得解.
解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,right0
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7-5<AE<7+5,
即7-5<2AD<7+5,
∴1<AD<6.
故选:B.
12、【答案】B
【解析】首先根据等边三角形的性质,得到BC=AC,CD=CE,∠ACB=∠BCD=60°,然后由SAS判定△BCD≌△ACE,根据全等三角形的对应边相等即可证得①正确;由全三角形的对应角相等,得到∠CBD=∠CAE,根据ASA证得△BCF≌△ACG,即可得到②正确,由于BC≠CD,∠CBF≠∠CDF,于是得到△BCF与△DCF不一定全等,③错误;根据三角形外角性质即可得出④正确.
解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,
在△BCD和△ACE中
∴△BCD≌△ACE(SAS),
∴AE=BD,∴①正确;
∠CBD=∠CAE,
∵∠BCA=∠ACG=60°,
∴在△BCF和△ACG中
∴△BCF≌△ACG(ASA),
∴AG=BF,∴②正确;
∵BC≠CD,∠CBF≠∠CDF,
∴△BCF与△DCF不一定全等,
∴③错误;
∵∠CDB=∠AEC,∠DCE=60°,
∴∠AOB=∠CBD+∠CEA=∠CBD+∠CDB=∠DCE=60°,
∴∠BOE=120°,
∴④正确.
故选:B.
填空题
13、【答案】4
【解析】由等腰三角形有两条边的长度之比为1:2,根据三角形的三边关系,可得腰长与底边长的比为2:1,又由等腰三角形的周长是40,即可求得这个等腰三角形的底边长,进而利用勾股定理得出等腰三角形底边上的高.
解:∵等腰三角形有两条边的长度之比为1:2,
∴腰长与底边长的比为:2:1,
∵等腰三角形的周长是40cm,
∴这个等腰三角形的底边长为:40×=8(cm),腰长为:16cm,
故这等腰三角形底边上的高是:=4(cm).
故答案为:4.
14、【答案】50°
【解析】根据全等三角形的性质得出∠D=∠C=30°,再根据三角形内角和定理求出即可.
解:∵△ABC≌△BAD,∠C=30°,
∴∠D=∠C=30°,
∵∠DBA=100°,
∴∠BAD=180°-∠D-∠DBA=180°-30°-100°=50°,
故答案为:50°.
15、【答案】2
【解析】如图,证明∠B=∠MAC;证明△ABN≌△CAM,得到AM=BN=3,AN=CM=5,即可解决问题.
right0解:∵BN⊥AN,AB⊥AC,
∴∠B+∠BAN=∠BAN+∠CAM,
∴∠B=∠MAC;
在△ABN与△CAM中,
,
∴△ABN≌△CAM(AAS),
∴AM=BN=3,AN=CM=5,
∴MN=5-3=2.
故答案为2.
16、【答案】122°
【解析】根据三角形内角和定理求出∠EDA+∠EAD=62°,根据等边三角形的性质得出AC=AD,∠CAD=60°,根据全等三角形的判定得出△ABC≌△DEA,根据全等三角形的性质得出∠B=∠E=118°,∠BAC=∠EDA,∠ACB=∠EAD,求出∠BAE=∠CAD+∠ADE+∠EAD,代入求出即可.
解:∵∠E=118°,
∴∠EDA+∠EAD=180°-∠E=180°-118°=62°,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
在△ABC和△DEA中
,
∴△ABC≌△DEA(SSS),
∴∠B=∠E=118°,∠BAC=∠EDA,∠ACB=∠EAD,
∴∠BAE=∠CAD+∠BAC+∠EAD=60°+∠ADE+∠EAD=60°+62°=122°,
故答案为:122°.
17、【答案】10
【解析】由已知利用角的平分线上的点到角的两边的距离相等可得到DE=CD,AC=AE,加上BC=AC,三角形的周长为BE+BD+DE=BE+CB=AE+BE,于是周长可得.
解:CD=DE
∵AC=BC
∴∠B=45°
∴DE=BE
∵△DEB的周长=DB+DE+BE=AC+BE=AB=10.
故填10.
18、【答案】①②③
【解析】由题意可证△AEP≌△CFP,可得:①AE=CF,②△EPF是等腰直角 三角形,③S四边形AEPF=S△ABC,即成立的为①②③.
解:∵AB=AC,∠BAC=90,点P是BC的中点,
∴AP=BP=CP,∠B=∠C=∠BAP=∠PAC=45°,AP⊥BC,S△APC=S△ABC,
∵∠APF+∠CPF=90°,∠APF+∠APE=90°,
∴∠APE=∠CPF且AP=PC,∠C=∠BAP=45°,
∴△AEP≌△CFP(ASA),
∴AE=CF,PF=PE,S△AEP=S△CFP,∠AEP=∠CPF,
∴△PEF是等腰直角三角形,S△APC=S四边形AEPF.
∴S四边形AEPF=S△ABC,
故①②③正确,
∵AP是定值,EF随PF的变化而变化,只有当PF⊥AC时,EF=AP,
∴④不正确,
故答案为:①②③.
【点睛】本题考查了旋转的性质,等腰三角形的性质,熟练运用这些性质是本题的关键.
三、解答题
19、【解析】先证明∠COD=∠AOB,然后根据“SAS”可证明△AOB≌△COD.
证明:∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD,
即∠COD=∠AOB,
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS).
20、【解析】根据等式的性质,可得∠BAC与∠CAE的关系,根据SAS,可得三角形全等,再根据全等三角形的性质,可得答案.
证明:∵∠1=∠2,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE? (SAS),
∴∠B=∠D.
21、【解析】首先利用“HL”证明Rt△ABC≌Rt△ABD,得出∠CAB=∠DAB,进一步利用“SAS”证得△ACE≌△ADE,证得∠CEA=∠DEA.
证明:∵AC⊥BC,AD⊥BD,
∴∠ACB=∠ADB=90°,
在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL),
∴∠CAB=∠DAB,
在△ACE和△ADE中
∴△ACE≌△ADE,
∴∠CEA=∠DEA.
22、【解析】由平行可得∠B=∠D,∠AEF=∠CFE,可求得∠AEB=∠CFD,又结合条件可得BE=DF,可证明△ABE≌△CDF,可得AB=CD.
证明:
∵AB∥CD,
∴∠B=∠D,
∵AE∥CF,
∴∠AEF=∠CFE,
∴∠AEB=∠CFD,
∵BF=DE,
∴BF-EF=DE-EF,即BE=DF,
在△ABE和△CDF中
∴△ABE≌△CDF(ASA),
∴AB=CD.
23、【解析】根据SSS证明△ADB与△BCA全等,进而利用全等三角形的性质得出∠CAB=∠DBA,进而得出OA=OB,利用等式的性质解答即可.
证明:在△ADB与△BCA中,
,
∴△ADB≌△BCA(SSS),
∴∠CAB=∠DBA,
∴OA=OB,
∴DB-OB=AC-OA,
∴OC=OD.
24、【解析】由BD为角平分线得到一对角相等,再由已知直角相等得到三角形AOD与三角形BDC相似,由相似三角形对应角相等得到一对角相等,再由对顶角相等,等量代换得到一对角相等,进而确定出三角形BCO与三角形BCD相似,利用相似三角形对应角相等得到∠BCO=∠BDC=∠ADO,再由对顶角相等,AO=BO,利用AAS得到三角形AOD与三角形BOC全等,利用全等三角形对应边相等得到OD=OC,利用等边对等角及等量代换即可得证.
证明:∵∠A=∠B=90°,BD平分∠ADC,即∠ADO=∠BDC,
∴△ADO∽△BDC,
∴∠AOD=∠BCD,
∵∠AOD=∠BOC,
∴∠BCD=∠BOC,
∵∠B=∠B,
∴△BCD∽△BOC,
∴∠BCO=∠BDC=∠ADO,
在△ADO和△BCO中,
,
∴△AOD≌△BCO(AAS),
∴OD=OC,
∴∠OCD=∠BDC,
∴∠OCD=∠BCO,
则CA平分∠DCB.
25、【解析】由已知角相等,利用邻补角定义及等角的余角相等得到一对角相等,且利用等角对等边得到AD=AE,利用SAS得到三角形ADB与三角形AEC全等,利用全等三角形对应边相等即可得证.
证明:∵∠ADE=∠AED,∠ADE+∠ADB=180°,∠AED+∠AEC=180°,
∴AD=AE,∠ADB=∠AEC,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴AB=AC.
26、【解析】(1)证明△ADE≌△FCE 得AE=FE,再由垂直平分线的性质得BA=BF,最后由等腰三角形的三线合一定理得结论;
(2)由全等三角形得AD=CF,再BA=BF,得结论.
解:(1)∵AD∥BC,
∴∠DAE=∠F,∠D=∠ECF,
∵E为CD中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE??(AAS),
∴AE=EF,
又∵BE⊥AE,
∴BA=BF,
∴BE平分∠ABC;
(2)由(1)知??AB=BF,
∵BF=BC+CF,
∴AB=BC+CF,
∵△ADE≌△FCE,
∵AD=CF,
∴AB=BC+AD.
单元测试题(2023年)(内含答案)
一、选择题:(共12题;每小题4分,共48分)
1、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A. 带①去 B. 带②去
C. 带③去 D. 带①和②去
2、如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A. ∠A=∠D B. ∠ACB=∠DBC
C. AC=DB D. AB=DC
3、如图,等腰三角形ABC中,AB=AC,∠A=40°,BD是△ABC的平分线,DE∥BC,则∠BDE的度数为( )
A. 20° B. 35° C. 40° D. 70°
4、到三角形三个顶点的距离都相等的点是( )
A. 两条中线的交点 B. 两条高的交点
C. 两条角平线的交点 D. 两条边的垂直平分线的交点
5、已知等腰中,,则的度数为( )
A. B.
C. 或 D. 或或
如图,在等腰三角形ABC中,AD是底边BC上的中线,DE是△ABD高线.图中与∠BAD一定相等的角有(不含本身)( )
A. 1个 B. 2个 C. 3个 D. 4个
7、如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.若∠B=75°,∠AFB=40°,则∠D的度数为( )
A. 60° B. 65° C. 70° D. 75°
8、在△ABC和△DEF中,已知AB=DE,∠A=∠D,下列条件:①AC=DF;②∠B=∠E;③∠C=∠F;④BC=EF.其中一定能判定△ABC≌△DEF的个数为( )
A. 1 B. 2 C. 3 D. 4
9、如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A. ∠B=∠E B. BC∥EF C. ∠BCA=∠F D. ∠A=∠EDF
10、在△ABC中,∠B=90°,CD平分∠ACB,DE⊥AC于点E,若AB=4cm,则AD+DE的值为( )
A. 3cm B. 4cm C. 5cm D. 6cm
11、在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是( )
A. 0<AD<12 B. 1<AD<6 C. 0<AD<6 D. 2<AD<12
12、如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接FG;下列结论:①AE=BD;②AG=BF;③△BCF≌△DCF;④∠BOE=120°.其中正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
二、填空题:(共6题;每小题4分,共24分)
13、如果等腰三角形的两条边的比是1:2,周长是40cm,那么这等腰三角形底边上的高是_____cm.
14、如图,已知△ABC≌△BAD,∠C=30°,∠DBA=100°,则∠BAD的度数为 _____.
如图,AB⊥AC,且AB=AC,BN⊥AN,CM⊥AN,若BN=3,CM=5,则MN=_____.
如图,五边形ABCDE中,△ACD是等边三角形、若AB=DE.BC=AE,∠E=118°,则∠BAE的度数是_____.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长是_____cm.
18、如图,已知在△ABC中,AB=AC,∠BAC=90,直角∠EPF顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下4个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内部绕顶点P旋转时(点E不与AB重合),上述结论始终成立的是________.
三、解答题:(共8题;共78分)
19、(8分)如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
20、(8分)如图,已知AB=AD,AC=AE,∠1=∠2
求证:∠B=∠D.
21、(10分)如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
求证:∠CEA=∠DEA.
22、(10分)如图,已知AB∥CD,AE∥CF,BF=DE
求证:AB=CD.
23、(10分)已知:如图AC、BD相交于点O,AC=BD,BC=AD,求证:OC=OD.
24、(10分)如图,BD平分∠ADC,∠A=∠B=90°,OA=OB.求证:CA平分∠DCB.
25、(10分)如图,已知点B、D、E、C在同一直线上,∠ADE=∠AED,BD=CE.
求证:AB=AC.
26、(12分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于F,
求证:(1)BE平分∠ABC
(2)AB=BC+AD
试卷答案
选择题
1、【答案】C
【解析】此题可以采用全等三角形的判定方法以及排除法进行分析,从而确定最后的答案.
解:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误;
B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误;
C、带③去,不但保留了原三角形的两个角还保留了其中一条边,符合ASA判定,故C选项正确;
D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D选项错误.
故选:C.
2、【答案】C
【解析】全等三角形的判定方法有SAS,ASA,AAS,SSS,根据定理逐个判断即可.
解:A、∠A=∠D,∠ABC=∠DCB,BC=BC,符合AAS,即能推出△ABC≌△DCB,故本选项错误;
B、∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合ASA,即能推出△ABC≌△DCB,故本选项错误;
C、∠ABC=∠DCB,AC=BD,BC=BC,不符合全等三角形的判定定理,即不能推出△ABC≌△DCB,故本选项正确;
D、AB=DC,∠ABC=∠DCB,BC=BC,符合SAS,即能推出△ABC≌△DCB,故本选项错误;
故选:C.
3、【答案】B
【解析】根据等腰三角形的性质推出∠ABC=70°,根据角平分线的定义得出∠DBC=35°,根据平行线的性质即可得解.
解:∵AB=AC,
∴∠ABC=∠C,
∵∠A=40°,
∴∠ABC=×(180°-40°)=70°,
∵BD是△ABC的平分线,
∴∠DBC=∠ABC=35°,
∵DE∥BC,
∴∠BDE=∠DBC=35°,
故选:B.
4、【答案】D
【解析】根据线段垂直分线的性质解答即可.
解:∵线段垂直平分线上任意一点,到线段两端点的距离相等,
∴到三角形三个顶点的距离都相等的点是两条边的垂直平分线的交点.
故选:D.
5、【答案】D
【解析】此题分为:为顶角、为顶角和、同为底角,再根据三角形内角和定理,等腰三角形的性质求得的度数.
解:当为顶角时,则;
当为顶角时,则;
当、为底角时,则.
故选:D.
【点睛】本题主要考查等腰三角形的性质,掌握等腰三角形的两底角相等是解题的关键,注意分类讨论.
6、【答案】B
【解析】由三线合一得∠DAC=∠BAD,再由直角三角形两个锐角互余得∠BAD=∠BDE.
解:∵△ABC为等腰三角形,AD是底边BC上的中线,
∴AD平分∠BAC,
∴∠DAC=∠BAD,
∵∠BAD+∠ADE=∠BDE+∠ADE=90°,
∴∠BAD=∠BDE,
∴∠BAD=∠BDE=∠DAC,
所以有2个角和它相等,
故选:B.
7、【答案】B
【解析】由BE=CF推导出BF=CE,即可根据全等三角形的判定定理“SAS”证明△ABF≌△DCE,则∠A=∠D=180°-75°-40°=65°,
解:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS),
∵∠B=75°,∠AFB=40°,
∴∠A=∠D=180°-∠B-∠AFB=180°-75°-40°=65°,
∴∠D的度数为65°,
故选:B.
8、【答案】C
【解析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理逐个判断即可.
解:如图,
①∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
故①正确;
②∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
故②正确;
③∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
故③正确;
④根据AB=DE,BC=EF,∠A=∠D不能推出△ABC≌△DEF,
∴④错误;
故选:C.
9、【答案】A
【解析】等三角形的判定方法SAS是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可.
解:∵AB=DE,BC=EF,
∴要使△ABC≌△DEF,
只要满足∠B=∠E或AC=BC即可,
故选:A.
10、【答案】B
【解析】先根据角平分线的性质得出BD=DE,进而可得出结论.
解:∵在△ABC中,∠B=90°,CD平分∠ACB,DE⊥AC于点E,
∴DE=BD.
∵AB=4cm,
∴AD+DE=AD+BD=AB=4cm.
故选:B.
11、【答案】B
【解析】作出图形,延长中线AD到E,使DE=AD,利用“边角边”证明△ACD和△EBD全等,根据全等三角形对应边相等可得AC=BE,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE的范围,再除以2即可得解.
解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,right0
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7-5<AE<7+5,
即7-5<2AD<7+5,
∴1<AD<6.
故选:B.
12、【答案】B
【解析】首先根据等边三角形的性质,得到BC=AC,CD=CE,∠ACB=∠BCD=60°,然后由SAS判定△BCD≌△ACE,根据全等三角形的对应边相等即可证得①正确;由全三角形的对应角相等,得到∠CBD=∠CAE,根据ASA证得△BCF≌△ACG,即可得到②正确,由于BC≠CD,∠CBF≠∠CDF,于是得到△BCF与△DCF不一定全等,③错误;根据三角形外角性质即可得出④正确.
解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,
在△BCD和△ACE中
∴△BCD≌△ACE(SAS),
∴AE=BD,∴①正确;
∠CBD=∠CAE,
∵∠BCA=∠ACG=60°,
∴在△BCF和△ACG中
∴△BCF≌△ACG(ASA),
∴AG=BF,∴②正确;
∵BC≠CD,∠CBF≠∠CDF,
∴△BCF与△DCF不一定全等,
∴③错误;
∵∠CDB=∠AEC,∠DCE=60°,
∴∠AOB=∠CBD+∠CEA=∠CBD+∠CDB=∠DCE=60°,
∴∠BOE=120°,
∴④正确.
故选:B.
填空题
13、【答案】4
【解析】由等腰三角形有两条边的长度之比为1:2,根据三角形的三边关系,可得腰长与底边长的比为2:1,又由等腰三角形的周长是40,即可求得这个等腰三角形的底边长,进而利用勾股定理得出等腰三角形底边上的高.
解:∵等腰三角形有两条边的长度之比为1:2,
∴腰长与底边长的比为:2:1,
∵等腰三角形的周长是40cm,
∴这个等腰三角形的底边长为:40×=8(cm),腰长为:16cm,
故这等腰三角形底边上的高是:=4(cm).
故答案为:4.
14、【答案】50°
【解析】根据全等三角形的性质得出∠D=∠C=30°,再根据三角形内角和定理求出即可.
解:∵△ABC≌△BAD,∠C=30°,
∴∠D=∠C=30°,
∵∠DBA=100°,
∴∠BAD=180°-∠D-∠DBA=180°-30°-100°=50°,
故答案为:50°.
15、【答案】2
【解析】如图,证明∠B=∠MAC;证明△ABN≌△CAM,得到AM=BN=3,AN=CM=5,即可解决问题.
right0解:∵BN⊥AN,AB⊥AC,
∴∠B+∠BAN=∠BAN+∠CAM,
∴∠B=∠MAC;
在△ABN与△CAM中,
,
∴△ABN≌△CAM(AAS),
∴AM=BN=3,AN=CM=5,
∴MN=5-3=2.
故答案为2.
16、【答案】122°
【解析】根据三角形内角和定理求出∠EDA+∠EAD=62°,根据等边三角形的性质得出AC=AD,∠CAD=60°,根据全等三角形的判定得出△ABC≌△DEA,根据全等三角形的性质得出∠B=∠E=118°,∠BAC=∠EDA,∠ACB=∠EAD,求出∠BAE=∠CAD+∠ADE+∠EAD,代入求出即可.
解:∵∠E=118°,
∴∠EDA+∠EAD=180°-∠E=180°-118°=62°,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
在△ABC和△DEA中
,
∴△ABC≌△DEA(SSS),
∴∠B=∠E=118°,∠BAC=∠EDA,∠ACB=∠EAD,
∴∠BAE=∠CAD+∠BAC+∠EAD=60°+∠ADE+∠EAD=60°+62°=122°,
故答案为:122°.
17、【答案】10
【解析】由已知利用角的平分线上的点到角的两边的距离相等可得到DE=CD,AC=AE,加上BC=AC,三角形的周长为BE+BD+DE=BE+CB=AE+BE,于是周长可得.
解:CD=DE
∵AC=BC
∴∠B=45°
∴DE=BE
∵△DEB的周长=DB+DE+BE=AC+BE=AB=10.
故填10.
18、【答案】①②③
【解析】由题意可证△AEP≌△CFP,可得:①AE=CF,②△EPF是等腰直角 三角形,③S四边形AEPF=S△ABC,即成立的为①②③.
解:∵AB=AC,∠BAC=90,点P是BC的中点,
∴AP=BP=CP,∠B=∠C=∠BAP=∠PAC=45°,AP⊥BC,S△APC=S△ABC,
∵∠APF+∠CPF=90°,∠APF+∠APE=90°,
∴∠APE=∠CPF且AP=PC,∠C=∠BAP=45°,
∴△AEP≌△CFP(ASA),
∴AE=CF,PF=PE,S△AEP=S△CFP,∠AEP=∠CPF,
∴△PEF是等腰直角三角形,S△APC=S四边形AEPF.
∴S四边形AEPF=S△ABC,
故①②③正确,
∵AP是定值,EF随PF的变化而变化,只有当PF⊥AC时,EF=AP,
∴④不正确,
故答案为:①②③.
【点睛】本题考查了旋转的性质,等腰三角形的性质,熟练运用这些性质是本题的关键.
三、解答题
19、【解析】先证明∠COD=∠AOB,然后根据“SAS”可证明△AOB≌△COD.
证明:∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD,
即∠COD=∠AOB,
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS).
20、【解析】根据等式的性质,可得∠BAC与∠CAE的关系,根据SAS,可得三角形全等,再根据全等三角形的性质,可得答案.
证明:∵∠1=∠2,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE? (SAS),
∴∠B=∠D.
21、【解析】首先利用“HL”证明Rt△ABC≌Rt△ABD,得出∠CAB=∠DAB,进一步利用“SAS”证得△ACE≌△ADE,证得∠CEA=∠DEA.
证明:∵AC⊥BC,AD⊥BD,
∴∠ACB=∠ADB=90°,
在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL),
∴∠CAB=∠DAB,
在△ACE和△ADE中
∴△ACE≌△ADE,
∴∠CEA=∠DEA.
22、【解析】由平行可得∠B=∠D,∠AEF=∠CFE,可求得∠AEB=∠CFD,又结合条件可得BE=DF,可证明△ABE≌△CDF,可得AB=CD.
证明:
∵AB∥CD,
∴∠B=∠D,
∵AE∥CF,
∴∠AEF=∠CFE,
∴∠AEB=∠CFD,
∵BF=DE,
∴BF-EF=DE-EF,即BE=DF,
在△ABE和△CDF中
∴△ABE≌△CDF(ASA),
∴AB=CD.
23、【解析】根据SSS证明△ADB与△BCA全等,进而利用全等三角形的性质得出∠CAB=∠DBA,进而得出OA=OB,利用等式的性质解答即可.
证明:在△ADB与△BCA中,
,
∴△ADB≌△BCA(SSS),
∴∠CAB=∠DBA,
∴OA=OB,
∴DB-OB=AC-OA,
∴OC=OD.
24、【解析】由BD为角平分线得到一对角相等,再由已知直角相等得到三角形AOD与三角形BDC相似,由相似三角形对应角相等得到一对角相等,再由对顶角相等,等量代换得到一对角相等,进而确定出三角形BCO与三角形BCD相似,利用相似三角形对应角相等得到∠BCO=∠BDC=∠ADO,再由对顶角相等,AO=BO,利用AAS得到三角形AOD与三角形BOC全等,利用全等三角形对应边相等得到OD=OC,利用等边对等角及等量代换即可得证.
证明:∵∠A=∠B=90°,BD平分∠ADC,即∠ADO=∠BDC,
∴△ADO∽△BDC,
∴∠AOD=∠BCD,
∵∠AOD=∠BOC,
∴∠BCD=∠BOC,
∵∠B=∠B,
∴△BCD∽△BOC,
∴∠BCO=∠BDC=∠ADO,
在△ADO和△BCO中,
,
∴△AOD≌△BCO(AAS),
∴OD=OC,
∴∠OCD=∠BDC,
∴∠OCD=∠BCO,
则CA平分∠DCB.
25、【解析】由已知角相等,利用邻补角定义及等角的余角相等得到一对角相等,且利用等角对等边得到AD=AE,利用SAS得到三角形ADB与三角形AEC全等,利用全等三角形对应边相等即可得证.
证明:∵∠ADE=∠AED,∠ADE+∠ADB=180°,∠AED+∠AEC=180°,
∴AD=AE,∠ADB=∠AEC,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴AB=AC.
26、【解析】(1)证明△ADE≌△FCE 得AE=FE,再由垂直平分线的性质得BA=BF,最后由等腰三角形的三线合一定理得结论;
(2)由全等三角形得AD=CF,再BA=BF,得结论.
解:(1)∵AD∥BC,
∴∠DAE=∠F,∠D=∠ECF,
∵E为CD中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE??(AAS),
∴AE=EF,
又∵BE⊥AE,
∴BA=BF,
∴BE平分∠ABC;
(2)由(1)知??AB=BF,
∵BF=BC+CF,
∴AB=BC+CF,
∵△ADE≌△FCE,
∵AD=CF,
∴AB=BC+AD.
