【北师大版】数学八年级下册课件:《1.2直角三角形》2
文档属性
| 名称 | 【北师大版】数学八年级下册课件:《1.2直角三角形》2 |  | |
| 格式 | zip | ||
| 文件大小 | 238.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-19 10:52:02 | ||
图片预览



文档简介
课件9张PPT。1.2直角三角形第一章 三角形的证明
我们曾经探索过直角三角形的哪些性质和判定方法(3)两直角边的平方和等于斜边的平方 (勾股理)。温故知新(1)有一个角是直角的三角形是直角三角形; (2)有两个角的和为90°的三角形是直角三角形; (3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形(1)有一个角是直角; (2)两个锐角的和为90°(互余 ); 定理 直角三角形两个锐角互余 。 定理 有两个角互余的三角形是直角三角形; 勾股理 两直角边的平方和等于斜边的平方 。如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
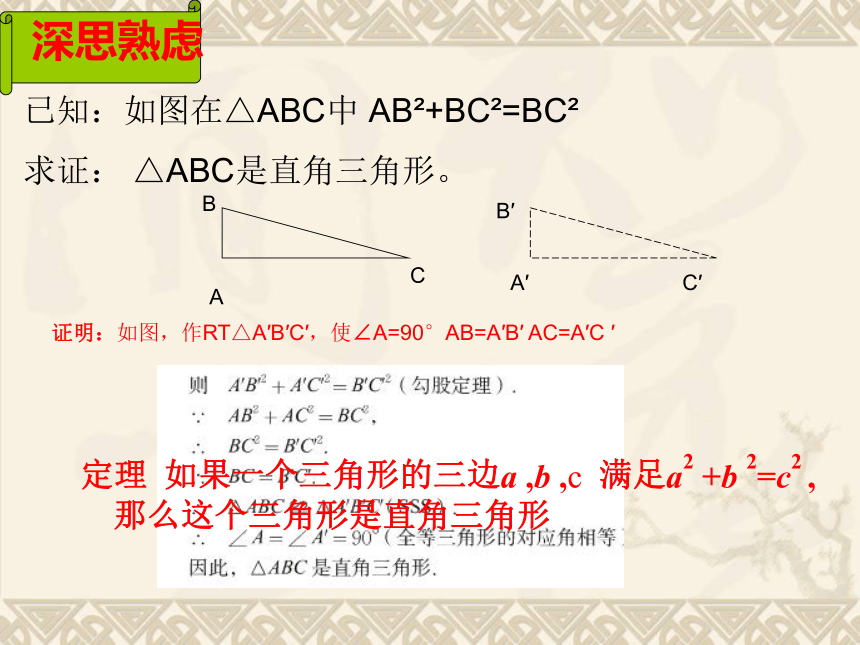
那么这个三角形是直角三角形吗?深思熟虑已知:如图在△ABC中 AB2+BC2=BC2
求证: △ABC是直角三角形。证明:如图,作RT△A′B′C′,使∠A=90°AB=A′B′ AC=A′C ′定理 如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形定理 直角三角形两个锐角互余 。 定理 有两个角互余的三角形是直角三角形; 勾股理 两直角边的平方和等于斜边的平方 。定理 如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形条件结论结论条件在观察下面三组命题议一议如果两个角是对顶角,那么它们相等,
如果两个角相等,那么它们是对顶角;如果小明患了肺炎,那么他一定会发烧,
如果小明发烧,那么他一定患了肺炎;三角形中相等的边所对的角相等,
三角形中相等的角所对的边相等.在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.如果一个定理的逆命题经过证明是真命题,那么她也是一个定理,其中一个称为另一个的逆定理你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗?1.说出下列命题的逆命题,并判断每对命题的真假:
(1).四边形是多边形;
(2).两直线平行,同旁内角互补;
(3).如果ab=0,那么a=0,b=0;再见
我们曾经探索过直角三角形的哪些性质和判定方法(3)两直角边的平方和等于斜边的平方 (勾股理)。温故知新(1)有一个角是直角的三角形是直角三角形; (2)有两个角的和为90°的三角形是直角三角形; (3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形(1)有一个角是直角; (2)两个锐角的和为90°(互余 ); 定理 直角三角形两个锐角互余 。 定理 有两个角互余的三角形是直角三角形; 勾股理 两直角边的平方和等于斜边的平方 。如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形吗?深思熟虑已知:如图在△ABC中 AB2+BC2=BC2
求证: △ABC是直角三角形。证明:如图,作RT△A′B′C′,使∠A=90°AB=A′B′ AC=A′C ′定理 如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形定理 直角三角形两个锐角互余 。 定理 有两个角互余的三角形是直角三角形; 勾股理 两直角边的平方和等于斜边的平方 。定理 如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形条件结论结论条件在观察下面三组命题议一议如果两个角是对顶角,那么它们相等,
如果两个角相等,那么它们是对顶角;如果小明患了肺炎,那么他一定会发烧,
如果小明发烧,那么他一定患了肺炎;三角形中相等的边所对的角相等,
三角形中相等的角所对的边相等.在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.如果一个定理的逆命题经过证明是真命题,那么她也是一个定理,其中一个称为另一个的逆定理你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗?1.说出下列命题的逆命题,并判断每对命题的真假:
(1).四边形是多边形;
(2).两直线平行,同旁内角互补;
(3).如果ab=0,那么a=0,b=0;再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
