2008届高三第二轮专题复习配套模拟数学试题(文科)
文档属性
| 名称 | 2008届高三第二轮专题复习配套模拟数学试题(文科) |

|
|
| 格式 | rar | ||
| 文件大小 | 182.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-08 00:00:00 | ||
图片预览



文档简介
2008届高三第二轮专题复习配套模拟考试(七)数学试题(文科)
一、选择题:本大题共12小题;每小题5分.共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的,把答案填写在答题卡相应位置上。
1. 设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则=
A.{4,5} B.{2,3} C.{1} D.{2}
2.箱内有大小相同的6个红球和4个黑球,从中每次取1个球记下颜色后再放回箱中,则前3次恰有1次取到黑球的概率为
A. B. C. D.
3.函数在处的导数等于 A 1 B 2 C 3 D 4
4. 要得到一个奇函数,只需将函数的图象
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
5. 空间四条直线a,b,c,d,满足a⊥b,b⊥c,c⊥d,d⊥a,则必有
A.a⊥c B.b⊥d C.b∥d 或a∥c D.b∥d 且a∥c
6. 一水池有两个进水口,一个出水口,每水口的进、出水速度如图甲、乙所示.某天
0点到6点,该水池的蓄水量如图丙所示.
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;
③4点到6点不进水不出水,则一定能确定正确的诊断是
A.① B.①② C.①③ D.①②③
7. 过正三棱锥侧棱与底面中心作截面,已知截面是等腰三角形,则侧面和底面所成角的余弦值为
A. B. C. 或 D. 或
8. 在中,,,则一定是
A 等腰三角形 B 等边三角形 C 锐角三角形 D 钝角三角形
9.已知等差数列的前项和为18,若,则的值为
A 21 B 9 C 27 D 36
10.已知双曲线的离心率为,若它的一条准线与抛物线的准线重合。设双曲线与抛物线的一个交点为,抛物线的焦点为,则
. . . .
11.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为
A B C D
12. 若,且,则
A. 2005 B. 2006 C. 2007 D. 2008
二、填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应位置上.
13 二项式的展开式的常数项是__________.
14 与椭圆有相同的焦距,且两准线间的距离为的双曲线方程为_ _.
15 一排7个座位,让甲、乙、丙三人就坐,要求甲与乙之间至少有一个空位,且甲与丙之间也至少有一个空位,则不同的坐法有 种.
16 给出以下结论:
①通项公式为的数列一定是以为首项,为公比的等比数列;
②若,则是第一、三象限的角;③函数在上是单调减函数;④若等差数列{}前n项和为,则三点共线。其中正确的是 .(请填写所有正确选项的序号)
2008届六中高三第二轮专题复习配套模拟考试(七)数学试题(文科)
班别 姓名: 座位 成绩
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
一、选择题:
二、填空题:
13 ;14 ;15 ;16 ;
三 解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17 (本小题满分10分)已知A、B、C的坐标分别为A(4,0),B(0,4), (1)若的值;(2)若的值.
18.(本小题满分12分) 设函数在及时取得极值.
(Ⅰ)求a、b的值;(Ⅱ)若对于任意的,都有成立,求c的取值范围.
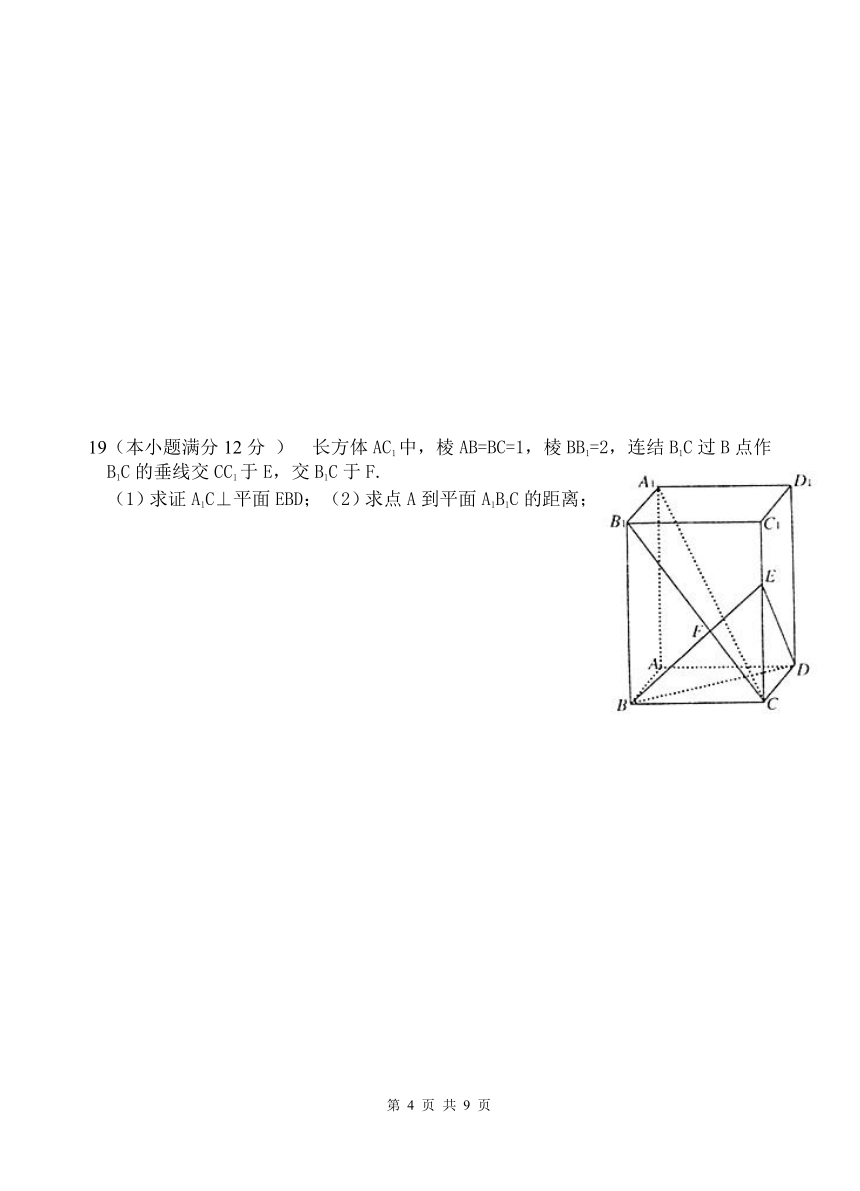
19(本小题满分12分 ) 长方体AC1中,棱AB=BC=1,棱BB1=2,连结B1C过B点作
B1C的垂线交CC1于E,交B1C于F.
(1)求证A1C⊥平面EBD; (2)求点A到平面A1B1C的距离;
20 (本小题满分12分)有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机掷一次,所得点数较大者获胜.(1)分别求出红色骰子投掷所得点数为8和蓝色骰子投掷所得点数为7的概率。(2)求投掷蓝色骰子者获胜的概率是多少?
21 (本小题满分12分)设各项均为正数的数列的前项和为,且满足: (1) 求; (2)求出数列的通项公式(写出推导过程);
(3) 设,求数列的前项和。
22 (本小题满分12分) 已知椭圆的方程为,双曲线的左、右焦点分别是的左、右顶点,而的左、右顶点分别是的左、右焦点。
(1)求双曲线的方程;(2)若直线与双曲线C2恒有两个不同的交点A和B,且(其中O为原点),求的范围。
2008届六中高三第二轮专题复习配套模拟考试(七)数学试题(文科)参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
D
C
A
C
B
C
D
A
D
二、填空题:
13 -540 ;14 或;15 100 ;16 ②④ ;
三 解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17解: ,
(1)由,……………… 2分
即
…………………… 5分
(2)由,得
解得 两边平方得……… 7分
…… 10分
18.解:(Ⅰ),因为函数在及取得极值,
则有,. 即解得,.……6分
(Ⅱ)由(Ⅰ)得,,.7当时,; 当时,; 当时,.…8分
所以,当时,取得极大值,又,.
则当时,的最大值为. ……10分
因为对于任意的,有恒成立,所以 , 解得 或,
因此的取值范围为.…12分
19.解:(1)连结AC,则AC⊥BD∵AC是A1C在平面ABCD内的射影 A1C⊥BD; …3分
又∵A1B1⊥面B1C1CB,且A1C在平面B1C1CB内的射影B1C⊥BE,
……6分
(2)易证:AB//平面A1B1C,所以点B到平面A1B1C的距离
等于点A到平面A1B1C的距离,……9分 又BF⊥平面A1B1C,
∴所求距离即为 …12分
20 解:(1)设红色骰子投掷所得点数为,蓝色骰子投掷所得点数,则; ……8分
(2)∵投掷骰子点数较大者获胜,∴投掷蓝色骰子者若获胜,则投掷后蓝色骰子点数为7,红色骰子点数为2.∴投掷蓝色骰子者获胜概率是………12分
21解:(1)由得解得…1分
由 解得 …2分由解得…3分
(2)当时当时,……4分
整理得: 化简得:……6分
所以是公差为2,首项为1的等差数列,即…7分
(3)………………9分
……12分
22解:解:(1)设双曲线的方程为 …… 1分
则,再由得,…… 2分
故的方程为 …… 3分
(2)将代入 得 … 4分
由直线与双曲线C2交于不同的两点得:
…… 6 分
且① …… 7分
设,则
又,得 即,解得:② ………10分 由①、②得:
故k的取值范围为 ………………………12分
一、选择题:本大题共12小题;每小题5分.共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的,把答案填写在答题卡相应位置上。
1. 设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则=
A.{4,5} B.{2,3} C.{1} D.{2}
2.箱内有大小相同的6个红球和4个黑球,从中每次取1个球记下颜色后再放回箱中,则前3次恰有1次取到黑球的概率为
A. B. C. D.
3.函数在处的导数等于 A 1 B 2 C 3 D 4
4. 要得到一个奇函数,只需将函数的图象
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
5. 空间四条直线a,b,c,d,满足a⊥b,b⊥c,c⊥d,d⊥a,则必有
A.a⊥c B.b⊥d C.b∥d 或a∥c D.b∥d 且a∥c
6. 一水池有两个进水口,一个出水口,每水口的进、出水速度如图甲、乙所示.某天
0点到6点,该水池的蓄水量如图丙所示.
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;
③4点到6点不进水不出水,则一定能确定正确的诊断是
A.① B.①② C.①③ D.①②③
7. 过正三棱锥侧棱与底面中心作截面,已知截面是等腰三角形,则侧面和底面所成角的余弦值为
A. B. C. 或 D. 或
8. 在中,,,则一定是
A 等腰三角形 B 等边三角形 C 锐角三角形 D 钝角三角形
9.已知等差数列的前项和为18,若,则的值为
A 21 B 9 C 27 D 36
10.已知双曲线的离心率为,若它的一条准线与抛物线的准线重合。设双曲线与抛物线的一个交点为,抛物线的焦点为,则
. . . .
11.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为
A B C D
12. 若,且,则
A. 2005 B. 2006 C. 2007 D. 2008
二、填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应位置上.
13 二项式的展开式的常数项是__________.
14 与椭圆有相同的焦距,且两准线间的距离为的双曲线方程为_ _.
15 一排7个座位,让甲、乙、丙三人就坐,要求甲与乙之间至少有一个空位,且甲与丙之间也至少有一个空位,则不同的坐法有 种.
16 给出以下结论:
①通项公式为的数列一定是以为首项,为公比的等比数列;
②若,则是第一、三象限的角;③函数在上是单调减函数;④若等差数列{}前n项和为,则三点共线。其中正确的是 .(请填写所有正确选项的序号)
2008届六中高三第二轮专题复习配套模拟考试(七)数学试题(文科)
班别 姓名: 座位 成绩
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
一、选择题:
二、填空题:
13 ;14 ;15 ;16 ;
三 解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17 (本小题满分10分)已知A、B、C的坐标分别为A(4,0),B(0,4), (1)若的值;(2)若的值.
18.(本小题满分12分) 设函数在及时取得极值.
(Ⅰ)求a、b的值;(Ⅱ)若对于任意的,都有成立,求c的取值范围.
19(本小题满分12分 ) 长方体AC1中,棱AB=BC=1,棱BB1=2,连结B1C过B点作
B1C的垂线交CC1于E,交B1C于F.
(1)求证A1C⊥平面EBD; (2)求点A到平面A1B1C的距离;
20 (本小题满分12分)有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机掷一次,所得点数较大者获胜.(1)分别求出红色骰子投掷所得点数为8和蓝色骰子投掷所得点数为7的概率。(2)求投掷蓝色骰子者获胜的概率是多少?
21 (本小题满分12分)设各项均为正数的数列的前项和为,且满足: (1) 求; (2)求出数列的通项公式(写出推导过程);
(3) 设,求数列的前项和。
22 (本小题满分12分) 已知椭圆的方程为,双曲线的左、右焦点分别是的左、右顶点,而的左、右顶点分别是的左、右焦点。
(1)求双曲线的方程;(2)若直线与双曲线C2恒有两个不同的交点A和B,且(其中O为原点),求的范围。
2008届六中高三第二轮专题复习配套模拟考试(七)数学试题(文科)参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
D
C
A
C
B
C
D
A
D
二、填空题:
13 -540 ;14 或;15 100 ;16 ②④ ;
三 解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17解: ,
(1)由,……………… 2分
即
…………………… 5分
(2)由,得
解得 两边平方得……… 7分
…… 10分
18.解:(Ⅰ),因为函数在及取得极值,
则有,. 即解得,.……6分
(Ⅱ)由(Ⅰ)得,,.7当时,; 当时,; 当时,.…8分
所以,当时,取得极大值,又,.
则当时,的最大值为. ……10分
因为对于任意的,有恒成立,所以 , 解得 或,
因此的取值范围为.…12分
19.解:(1)连结AC,则AC⊥BD∵AC是A1C在平面ABCD内的射影 A1C⊥BD; …3分
又∵A1B1⊥面B1C1CB,且A1C在平面B1C1CB内的射影B1C⊥BE,
……6分
(2)易证:AB//平面A1B1C,所以点B到平面A1B1C的距离
等于点A到平面A1B1C的距离,……9分 又BF⊥平面A1B1C,
∴所求距离即为 …12分
20 解:(1)设红色骰子投掷所得点数为,蓝色骰子投掷所得点数,则; ……8分
(2)∵投掷骰子点数较大者获胜,∴投掷蓝色骰子者若获胜,则投掷后蓝色骰子点数为7,红色骰子点数为2.∴投掷蓝色骰子者获胜概率是………12分
21解:(1)由得解得…1分
由 解得 …2分由解得…3分
(2)当时当时,……4分
整理得: 化简得:……6分
所以是公差为2,首项为1的等差数列,即…7分
(3)………………9分
……12分
22解:解:(1)设双曲线的方程为 …… 1分
则,再由得,…… 2分
故的方程为 …… 3分
(2)将代入 得 … 4分
由直线与双曲线C2交于不同的两点得:
…… 6 分
且① …… 7分
设,则
又,得 即,解得:② ………10分 由①、②得:
故k的取值范围为 ………………………12分
同课章节目录
