3.3 勾股定理的简单应用 课时 练习 (无答案)2023-3024学年 苏科版数学八年级上册
文档属性
| 名称 | 3.3 勾股定理的简单应用 课时 练习 (无答案)2023-3024学年 苏科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 150.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 00:00:00 | ||
图片预览

文档简介
3.3《勾股定理的简单应用》课时练习
一 、选择题
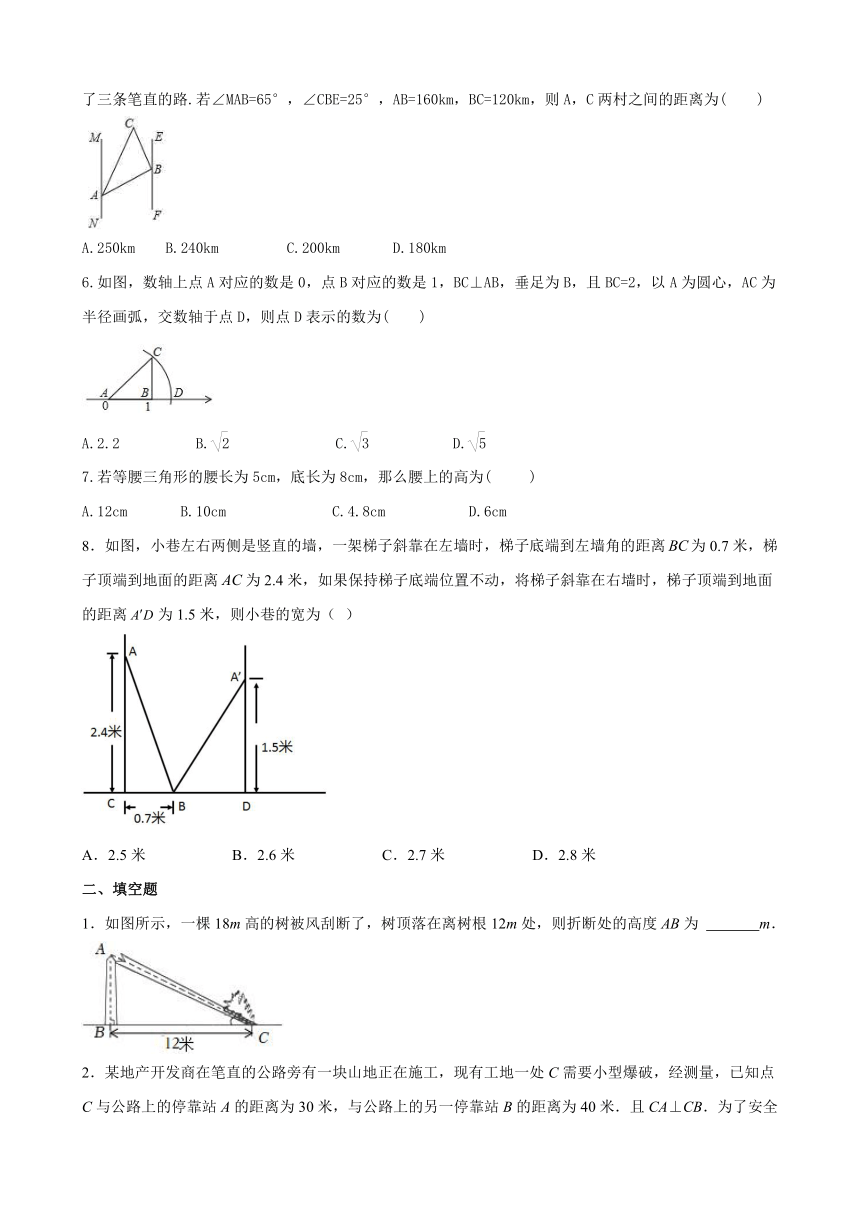
1.如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺 B.8尺 C.8.5尺 D.9尺
2.如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门铃5m及5m以内时,门铃就会自动发出语音“欢迎光临”.如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则BD的长为( )
A.3米 B.4米 C.5米 D.7米
3.北京冬奥会期间,中国运动健儿取得优异成绩.冬奥会的志愿者团队,给人留下了深刻印象,人人都是志愿者.作为志愿者的小颖,从窗户向外望,看到一人为快速从A处到达居住楼B处,直接从边长为24米的正方形草地中穿过.为保护草地,小颖计划在A处立一个标牌:“少走?米,踏之何忍”,已知B,C两处的距离为7米,那么标牌上?处的数字是( )
A.3 B.4 C.5 D.6
4.一根竹竿插到水池中离岸边1.5m远的水底,竹竿高出水面0.5m,若把竹竿的顶端拉向岸边,则竿顶刚好接触到岸边,并且和水面一样高,问水池的深度为( )
A.2m B.2.5cm C.2.25m D.3m
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160km,BC=120km,则A,C两村之间的距离为( )
A.250km B.240km C.200km D.180km
6.如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2 B. C. D.
7.若等腰三角形的腰长为5cm,底长为8cm,那么腰上的高为( )
A.12cm B.10cm C.4.8cm D.6cm
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,梯子顶端到地面的距离为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5米,则小巷的宽为( )
A.2.5米 B.2.6米 C.2.7米 D.2.8米
二 、填空题
1.如图所示,一棵18m高的树被风刮断了,树顶落在离树根12m处,则折断处的高度AB为 m.
2.某地产开发商在笔直的公路旁有一块山地正在施工,现有工地一处C需要小型爆破,经测量,已知点C与公路上的停靠站A的距离为30米,与公路上的另一停靠站B的距离为40米.且CA⊥CB.为了安全起见,已知进入爆破点C周围半径25米范围内有危险.问在进行爆破时,公路AB段是否因有危险而需要暂时封锁?答: .
3.如图,某学校(A点)到公路(直线l)的距离为300米,到公交车站(D点)的距离为500米,现要在公路边上建一个商店(C点),使之到学校A及到车站D的距离相等,则商店C与车站D之间的距离是 米.
4.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7m,梯子顶端D到地面的距离DE为2.4m,若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为1.5m,则这两面直立墙壁之间的安全通道的宽BE为 m.
5.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC中点.若动点E以1cm/s速度从A点出发,沿着A→B→A的方向运动,设E点运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t值为 .
三 、解答题
1.如图,城心公园的著名景点B在大门A的正北方向,游客可以从大门A沿正西方向行至景点C,然后沿笔直的赏花步道到达景点B;也可以从大门A沿正东方向行至景点D,然后沿笔直的临湖步道到达大门A的正北方的景点E,继续沿正北方向行至景点B(点A,B,C,D,E在同一平面内),其中AC=500米,BC=1300米,AD=600米,BE=400米.
(1)求A,B两点的距离;
(2)为增强游客的游览体验,提升公园品质,将从大门A修建一条笔直的玻璃廊桥AF与临湖步道DE交汇于点F,且玻璃廊桥AF垂直于临湖步道DE,求玻璃廊桥AF的长.
2如图,在吴中区上方山动物园里有两只猴子在一棵树 上的点 处,且 ,它们都要到池塘 处吃东西,其中一只猴子甲沿树爬至 再沿 走到离树 处的池塘 处,另一只猴子乙先爬到树顶 处后再沿缆绳 线段滑到 处.已知猴子甲所经过的路程比猴子乙所经过的路程多 ,设 为 .
(1) 请用含有 的整式表示线段 的长为 .
(2) 求这棵树高有多少米?
3在一条东西走向河的一侧有一村庄 ,河边原有两个取水点 ,,其中 ,由于某种原因,由 到 的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点 (,, 在一条直线上),并新修建一条路 ,测得 千米, 千米, 千米.
(1) 问 是否为从村庄 到河边的最近路?请通过计算加以说明.
(2) 求原来的路线 的长.
4在甲村至乙村的公路旁有一块山地正在开发,现有一 处需要爆破,已知点 与公路上的停靠站 的距离为 米,与公路上另一停靠站 的距离为 米,且 ,如图,为了安全起见,爆破点 周围半径 米范围内不得进入,问在进行爆破时,公路 段是否有危险,是否而需要暂时封锁?请通过计算进行说明.
5.如图,在平面直角坐标系中,点A(0,12),点B(m,12),且B到原点O的距离OB=20,动点P从原点O出发,沿路线O→A→B运动到点B停止,速度为每秒5个单位长度,同时,点Q从点B出发沿路线B→A→O运动到原点O停止,速度为每秒2个单位长度.设运动时间为t.
(1)求出P、Q相遇时点P的坐标.
(2)当P运动到AB边上时,连接OP、OQ,若△OPQ的面积为6,求t的值.
一 、选择题
1.如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺 B.8尺 C.8.5尺 D.9尺
2.如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门铃5m及5m以内时,门铃就会自动发出语音“欢迎光临”.如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则BD的长为( )
A.3米 B.4米 C.5米 D.7米
3.北京冬奥会期间,中国运动健儿取得优异成绩.冬奥会的志愿者团队,给人留下了深刻印象,人人都是志愿者.作为志愿者的小颖,从窗户向外望,看到一人为快速从A处到达居住楼B处,直接从边长为24米的正方形草地中穿过.为保护草地,小颖计划在A处立一个标牌:“少走?米,踏之何忍”,已知B,C两处的距离为7米,那么标牌上?处的数字是( )
A.3 B.4 C.5 D.6
4.一根竹竿插到水池中离岸边1.5m远的水底,竹竿高出水面0.5m,若把竹竿的顶端拉向岸边,则竿顶刚好接触到岸边,并且和水面一样高,问水池的深度为( )
A.2m B.2.5cm C.2.25m D.3m
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160km,BC=120km,则A,C两村之间的距离为( )
A.250km B.240km C.200km D.180km
6.如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2 B. C. D.
7.若等腰三角形的腰长为5cm,底长为8cm,那么腰上的高为( )
A.12cm B.10cm C.4.8cm D.6cm
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,梯子顶端到地面的距离为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5米,则小巷的宽为( )
A.2.5米 B.2.6米 C.2.7米 D.2.8米
二 、填空题
1.如图所示,一棵18m高的树被风刮断了,树顶落在离树根12m处,则折断处的高度AB为 m.
2.某地产开发商在笔直的公路旁有一块山地正在施工,现有工地一处C需要小型爆破,经测量,已知点C与公路上的停靠站A的距离为30米,与公路上的另一停靠站B的距离为40米.且CA⊥CB.为了安全起见,已知进入爆破点C周围半径25米范围内有危险.问在进行爆破时,公路AB段是否因有危险而需要暂时封锁?答: .
3.如图,某学校(A点)到公路(直线l)的距离为300米,到公交车站(D点)的距离为500米,现要在公路边上建一个商店(C点),使之到学校A及到车站D的距离相等,则商店C与车站D之间的距离是 米.
4.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7m,梯子顶端D到地面的距离DE为2.4m,若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为1.5m,则这两面直立墙壁之间的安全通道的宽BE为 m.
5.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC中点.若动点E以1cm/s速度从A点出发,沿着A→B→A的方向运动,设E点运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t值为 .
三 、解答题
1.如图,城心公园的著名景点B在大门A的正北方向,游客可以从大门A沿正西方向行至景点C,然后沿笔直的赏花步道到达景点B;也可以从大门A沿正东方向行至景点D,然后沿笔直的临湖步道到达大门A的正北方的景点E,继续沿正北方向行至景点B(点A,B,C,D,E在同一平面内),其中AC=500米,BC=1300米,AD=600米,BE=400米.
(1)求A,B两点的距离;
(2)为增强游客的游览体验,提升公园品质,将从大门A修建一条笔直的玻璃廊桥AF与临湖步道DE交汇于点F,且玻璃廊桥AF垂直于临湖步道DE,求玻璃廊桥AF的长.
2如图,在吴中区上方山动物园里有两只猴子在一棵树 上的点 处,且 ,它们都要到池塘 处吃东西,其中一只猴子甲沿树爬至 再沿 走到离树 处的池塘 处,另一只猴子乙先爬到树顶 处后再沿缆绳 线段滑到 处.已知猴子甲所经过的路程比猴子乙所经过的路程多 ,设 为 .
(1) 请用含有 的整式表示线段 的长为 .
(2) 求这棵树高有多少米?
3在一条东西走向河的一侧有一村庄 ,河边原有两个取水点 ,,其中 ,由于某种原因,由 到 的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点 (,, 在一条直线上),并新修建一条路 ,测得 千米, 千米, 千米.
(1) 问 是否为从村庄 到河边的最近路?请通过计算加以说明.
(2) 求原来的路线 的长.
4在甲村至乙村的公路旁有一块山地正在开发,现有一 处需要爆破,已知点 与公路上的停靠站 的距离为 米,与公路上另一停靠站 的距离为 米,且 ,如图,为了安全起见,爆破点 周围半径 米范围内不得进入,问在进行爆破时,公路 段是否有危险,是否而需要暂时封锁?请通过计算进行说明.
5.如图,在平面直角坐标系中,点A(0,12),点B(m,12),且B到原点O的距离OB=20,动点P从原点O出发,沿路线O→A→B运动到点B停止,速度为每秒5个单位长度,同时,点Q从点B出发沿路线B→A→O运动到原点O停止,速度为每秒2个单位长度.设运动时间为t.
(1)求出P、Q相遇时点P的坐标.
(2)当P运动到AB边上时,连接OP、OQ,若△OPQ的面积为6,求t的值.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
