2023-—2024学年苏科版数学八年级上册 期中培优训练试题(无答案)
文档属性
| 名称 | 2023-—2024学年苏科版数学八年级上册 期中培优训练试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 322.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 16:49:40 | ||
图片预览

文档简介
2023-—2024学年苏科版数学八年级上册 期中培优训练
一、单选题
1.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到 MBC≌ ABC,所以测得MB的长就是A,B两点间的距离,这里判定 MBC≌ ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
2.已知 、 、 是三角形的三边长,如果满足 ,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
3.如图,在△ABC中,,点D在AB上,将△ABC沿CD折叠,点B落在边AC上的点E处,若,则∠A的度数为( )
A.25° B.30° C.35° D.40°
4.如图,∠AOB=30°,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
A.6 B.12 C.16 D.20
5.满足下列条件的是直角三角形的是( )
A. , , B. , ,
C. D.
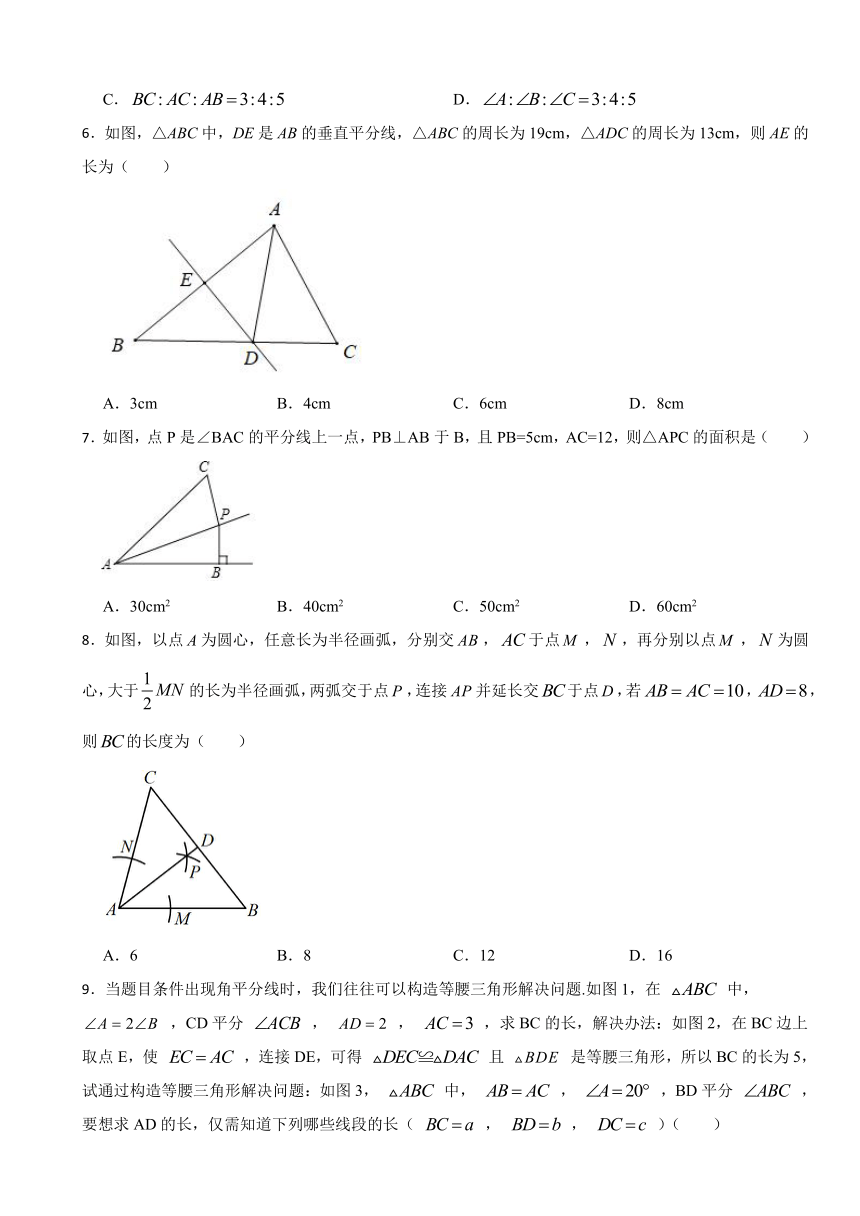
6.如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( )
A.3cm B.4cm C.6cm D.8cm
7.如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )
A.30cm2 B.40cm2 C.50cm2 D.60cm2
8.如图,以点为圆心,任意长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,连接并延长交于点,若,,则的长度为( )
A.6 B.8 C.12 D.16
9.当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题.如图1,在 中, ,CD平分 , , ,求BC的长,解决办法:如图2,在BC边上取点E,使 ,连接DE,可得 且 是等腰三角形,所以BC的长为5,试通过构造等腰三角形解决问题:如图3, 中, , ,BD平分 ,要想求AD的长,仅需知道下列哪些线段的长( , , )( )
A.a和b B.b和c C.a和c D.a、b和c
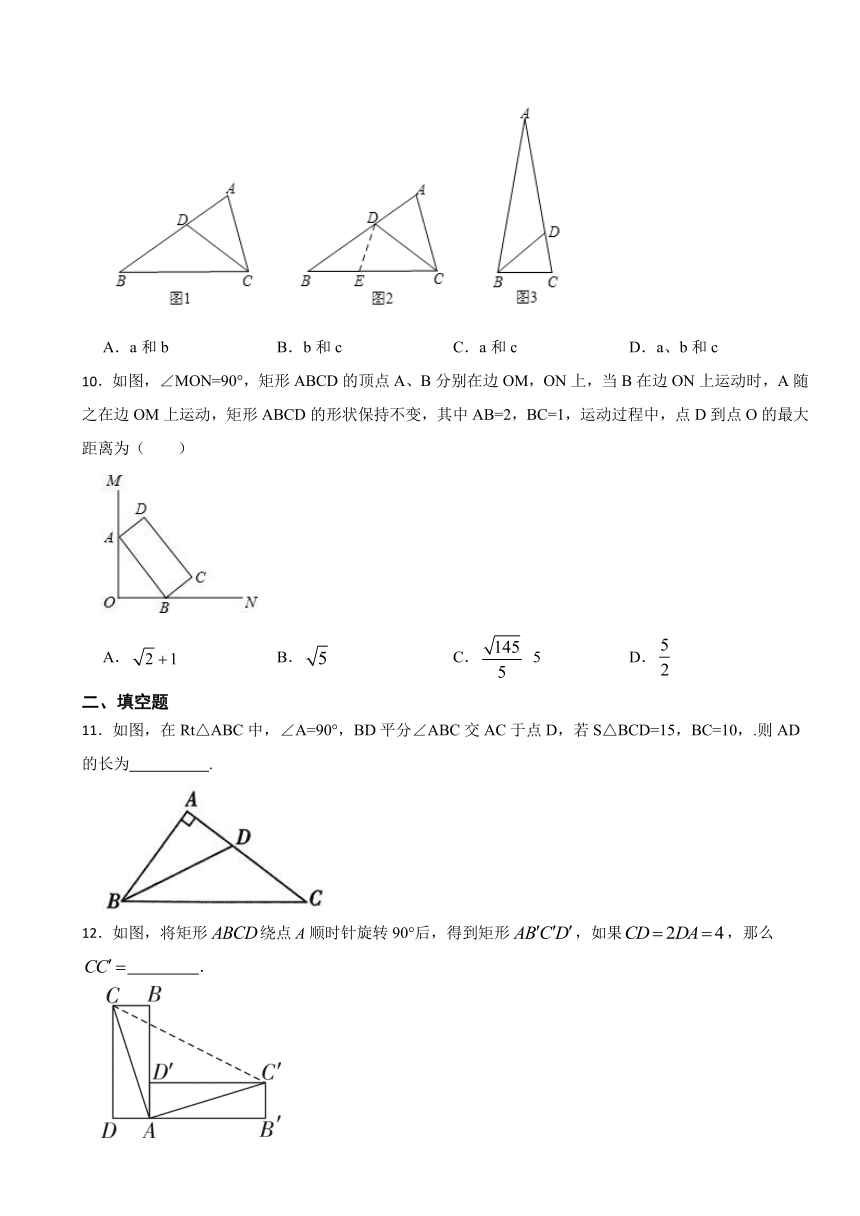
10.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A. B. C. 5 D.
二、填空题
11.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,若S△BCD=15,BC=10,.则AD的长为 .
12.如图,将矩形绕点顺时针旋转90°后,得到矩形,如果,那么 .
13.如图,在中,,平分,与边交于点,,若点到的距离等于5cm,则的长为 cm.
14.借助如图所示的“三等分角仪”等三等分某些度数的角,这个“三等分角仪”由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,,点D,E可在槽中滑动.若,则 °.
15.等边 内有一点 ,连结 , ,分别以 , 为边向外作等边三角形, 与 交于点 , 与 交于点 ,记 ,四边形 , , 的面积分别为 , , , ,若 , , ,则 的长度为 .
三、解答题
16.木工师傅做一个三角形屋梁架 ABC,如图所示,上弦 AB=AC=4m,跨度 BC 为 6m, 为牢固起见,还需做一根中柱 AD(AD 是△ABC 的中线)加以连接,现有一根长为 3m 的木料, 请你通过计算说明这根木料的长度是否适合加工成中柱 AD.
17.如图,在四边形ABCD中,∠B=90°,AB=2,BC=CD=2,AD=2,求∠ACD的度数.
18.如图,AC与BD相交于点O,AO=DO,∠A=∠D.求证:△ABO≌△DCO.
19.如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AB=DE.
求证:△ABC≌△DEF.
20.如图,从高8米的电线杆 的顶部 处,向地面的固定点 处拉一根铁丝,若 点距电线杆底部的距离为6米,现在准备一根长为12米的铁丝,够用吗?请你说明理由.
21.如图,△ABC中,AB=6,AC=7,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于E、F. 求△AEF的周长.
22.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上移动时,α与β之间有什么数量关系?请画出图形,并直接写出你的结论.
一、单选题
1.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到 MBC≌ ABC,所以测得MB的长就是A,B两点间的距离,这里判定 MBC≌ ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
2.已知 、 、 是三角形的三边长,如果满足 ,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
3.如图,在△ABC中,,点D在AB上,将△ABC沿CD折叠,点B落在边AC上的点E处,若,则∠A的度数为( )
A.25° B.30° C.35° D.40°
4.如图,∠AOB=30°,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
A.6 B.12 C.16 D.20
5.满足下列条件的是直角三角形的是( )
A. , , B. , ,
C. D.
6.如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( )
A.3cm B.4cm C.6cm D.8cm
7.如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )
A.30cm2 B.40cm2 C.50cm2 D.60cm2
8.如图,以点为圆心,任意长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧交于点,连接并延长交于点,若,,则的长度为( )
A.6 B.8 C.12 D.16
9.当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题.如图1,在 中, ,CD平分 , , ,求BC的长,解决办法:如图2,在BC边上取点E,使 ,连接DE,可得 且 是等腰三角形,所以BC的长为5,试通过构造等腰三角形解决问题:如图3, 中, , ,BD平分 ,要想求AD的长,仅需知道下列哪些线段的长( , , )( )
A.a和b B.b和c C.a和c D.a、b和c
10.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A. B. C. 5 D.
二、填空题
11.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,若S△BCD=15,BC=10,.则AD的长为 .
12.如图,将矩形绕点顺时针旋转90°后,得到矩形,如果,那么 .
13.如图,在中,,平分,与边交于点,,若点到的距离等于5cm,则的长为 cm.
14.借助如图所示的“三等分角仪”等三等分某些度数的角,这个“三等分角仪”由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,,点D,E可在槽中滑动.若,则 °.
15.等边 内有一点 ,连结 , ,分别以 , 为边向外作等边三角形, 与 交于点 , 与 交于点 ,记 ,四边形 , , 的面积分别为 , , , ,若 , , ,则 的长度为 .
三、解答题
16.木工师傅做一个三角形屋梁架 ABC,如图所示,上弦 AB=AC=4m,跨度 BC 为 6m, 为牢固起见,还需做一根中柱 AD(AD 是△ABC 的中线)加以连接,现有一根长为 3m 的木料, 请你通过计算说明这根木料的长度是否适合加工成中柱 AD.
17.如图,在四边形ABCD中,∠B=90°,AB=2,BC=CD=2,AD=2,求∠ACD的度数.
18.如图,AC与BD相交于点O,AO=DO,∠A=∠D.求证:△ABO≌△DCO.
19.如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AB=DE.
求证:△ABC≌△DEF.
20.如图,从高8米的电线杆 的顶部 处,向地面的固定点 处拉一根铁丝,若 点距电线杆底部的距离为6米,现在准备一根长为12米的铁丝,够用吗?请你说明理由.
21.如图,△ABC中,AB=6,AC=7,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于E、F. 求△AEF的周长.
22.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上移动时,α与β之间有什么数量关系?请画出图形,并直接写出你的结论.
同课章节目录
