二 项 式 定 理
图片预览


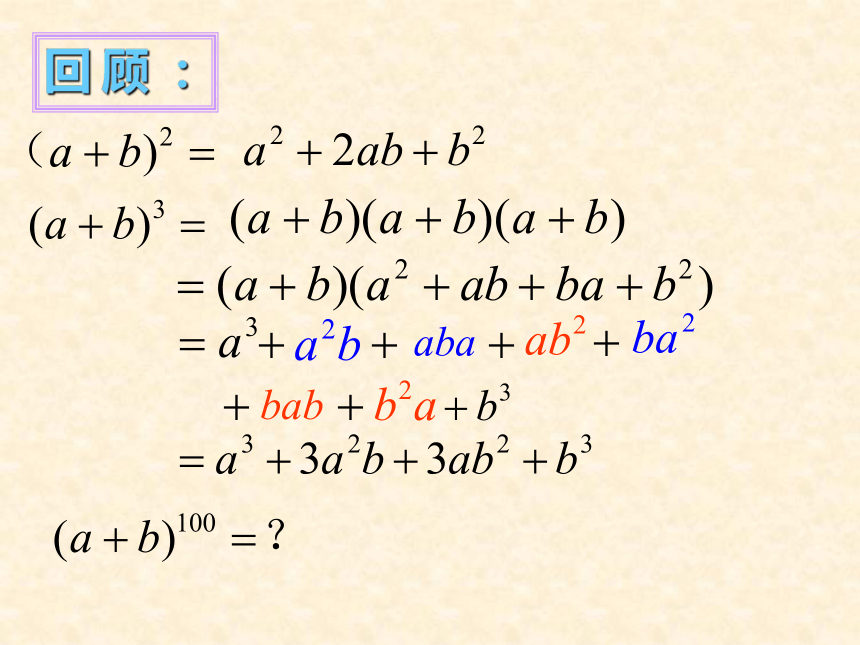



文档简介
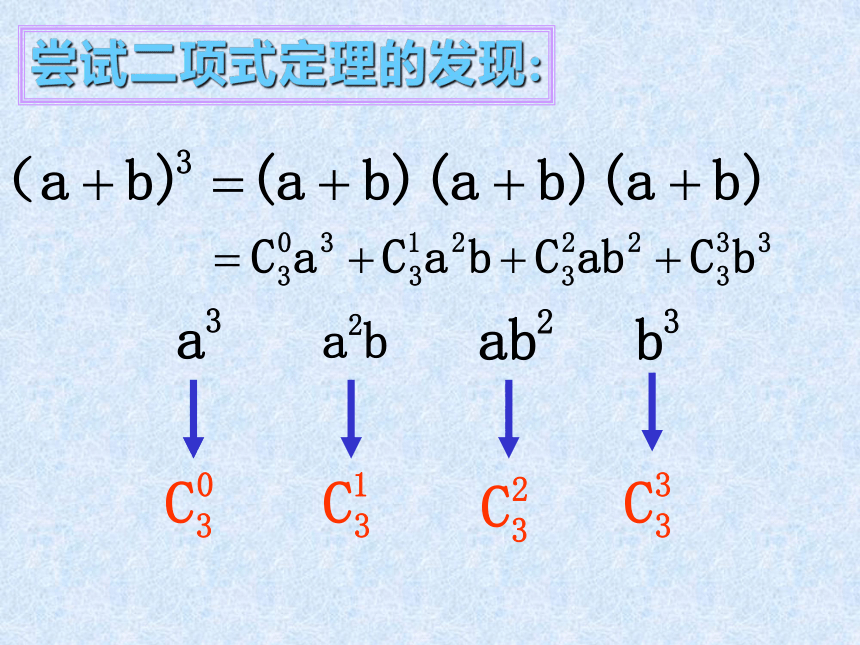
课件17张PPT。高二数学课二 项 式 定 理问题探究:(1)今天是星期五,那么7天后 (4)如果是 天后的这一天呢? 的这一天是星期几呢?(2)如果是15天后的这一天呢?(星期五)(3)如果是24天后的这一天呢?(星期六)(星期一)回顾:尝试二项式定理的发现:…尝试二项式定理的发现:尝试二项式定理的发现:……探求得:探求得:1.右边多项式为n+1项,各项系数为 (r=0,1,…,n)称为二项式系数。小结:2. 叫二项式展开式的通项。即 3.若令a=1,b=x则有公式尝试二项式定理的应用:例1:②③若上式中的“+”变为“-”呢?尝试二项式定理的应用:Ⅰ)求常数项Ⅱ)求展开式的整式项例2:尝试二项式定理的应用:练习:4040x2问题探究:(1)今天是星期五,那么7天后 (4)如果是 天后的这一天呢? 的这一天是星期几呢?(2)如果是15天后的这一天呢?(星期五)(3)如果是24天后的这一天呢?(星期六)(星期一)问题探究: 余数是1,所以是星期六探究:若将 除以9,则得到的余数是多少? 所以余数是1,小结:1)主要学习了二项式定理的探求极其 简单的应用。 2)思想方法:特殊到一般的方法 3)学会对问题进行探究 作业:课本46页习题4.7
T 1 , T 2 , T 5.问题:(1)今天是星期五,那么7天后 (4)如果是 天后的这一天呢? 的这一天是星期几呢?(2)如果是15天后的这一天呢?(星期六)(星期五)(3)如果是24天后的这一天呢?(星期一)
T 1 , T 2 , T 5.问题:(1)今天是星期五,那么7天后 (4)如果是 天后的这一天呢? 的这一天是星期几呢?(2)如果是15天后的这一天呢?(星期六)(星期五)(3)如果是24天后的这一天呢?(星期一)
