2023-2024学年盐城市八年级数学上期中模拟试卷(第1-3章)(含答案)
文档属性
| 名称 | 2023-2024学年盐城市八年级数学上期中模拟试卷(第1-3章)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 07:07:06 | ||
图片预览




文档简介
2023-2024学年盐城市八年级数学上期中模拟试卷(第1-3章)
(时间:100分钟 满分:120分)
一.选择题(24分)
1.在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
2.勾股定理是历史是第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B.C. D.
3.如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°则∠O的度数为( )
A.10° B.15° C.18° D.20°
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )
A.15cm B.13cm C.11cm D.9cm
5.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
6.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
A.3cm B.4cm C.5cm D.6cm
第6题图 第7题图 第8题图
7. 如图,点、分别是边长为的等边边、上的动点,点从顶点,点从顶点同时出发,且它们的速度都为,下面四个结论:①②≌③的度数不变,始终等于④当第秒或第秒时,为直角三角形,正确的有( )个.
A. B. C. D.
8.在中,,,、为上两点,,为外一点,且,,则下列结论:①;②;③;④,其中正确的是( )
A.①②③④ B.②③ C.①②④ D.①③④
二.填空题(24分)
9.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 度.
第9题图 第10题图 第11题图 第12题图
10.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为 .
11.如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为 厘米/秒.
12.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
13.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是 cm.
第13题图 第14题图 第15题图 第16题图
14.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点,则BE的长为 .
15.如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
16.如图,,点M、N分别在射线OA、OB上,MN=6,△OMN的面积为12,P是直线MN上的动点,点P关于OA对称的点为,点P关于OB对称的点为,当点P在直线NM上运动时,的面积最小值为______.
三.解答题(72分)
17.(6分)如图,方格纸上画有AB、CD两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法)
(1)请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;
(2)请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形,请画出所有
情形.
18.(8分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
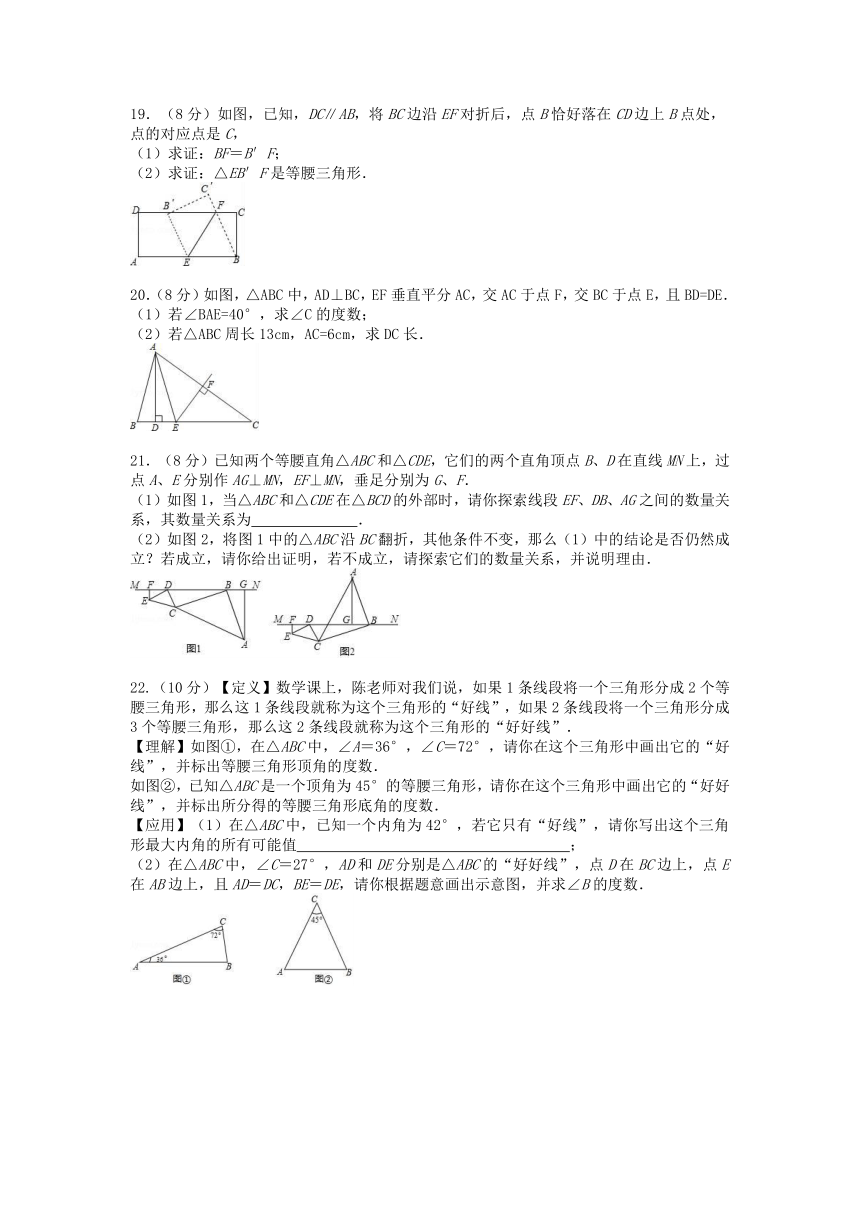
19.(8分)如图,已知,DC∥AB,将BC边沿EF对折后,点B恰好落在CD边上B点处,点的对应点是C,
(1)求证:BF=B′F;
(2)求证:△EB′F是等腰三角形.
20.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长13cm,AC=6cm,求DC长.
21.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
22.(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
23.(12分)(1)阅读理解: 如图①,在△ABC中,若AB=8,AC=12,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,体现了转化和化归的数学思想,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DM⊥DN于点D,DM交AB于点M,DN交AC于点N,连接MN,求证:BM+CN>MN;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=110°,以C为顶点作一个55°角,角的两边分别交AB,AD于M、N两点,连接MN,探索线段BM,DN,MN之间的数量关系,并加以证明.
24.(12分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
【小试牛刀】把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,S△EBC= ,S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
【知识运用】(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP 的距离.
教师样卷
一.选择题(24分)
1.在下列各组条件中,不能说明△ABC≌△DEF的是( B )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
2.勾股定理是历史是第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( A )
A. B.C. D.
3.如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°则∠O的度数为( C )
A.10° B.15° C.18° D.20°
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( B )
A.15cm B.13cm C.11cm D.9cm
5.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( C )
A.1个 B.2个 C.3个 D.4个
6.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( C )
A.3cm B.4cm C.5cm D.6cm
第6题图 第7题图 第8题图
7. 如图,点、分别是边长为的等边边、上的动点,点从顶点,点从顶点同时出发,且它们的速度都为,下面四个结论:①②≌③的度数不变,始终等于④当第秒或第秒时,为直角三角形,正确的有( C )个.
A. B. C. D.
解:∵点、速度相同,∴.在和中,,
∴≌,故②正确.则.
.∴.则,故③正确.
∵不一定等于.∴.∴.故①错误.设时间为t,则AP=BQ=t,PB=4-t①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得6-t=2t,t=2 ;②当∠BPQ=90°时,
∵∠B=60°,∴BQ=2BP,得t=2(6-t),t=4;∴当第2秒或第4秒时,△PBQ为直角三角形.
∴④正确.故选C.
8.在中,,,、为上两点,,为外一点,且,,则下列结论:①;②;③;④,其中正确的是( C )
A.①②③④ B.②③ C.①②④ D.①③④
解:∵,,,∴,
,∴,∵,,
∴,∵,∴,∴,∴,故①正确;由①中证明,∴,∵,,∴,∴,连接,∵,∴,∵,,∴,故②正确;
设与的交点为,∵,,∴,,
∴,故③错误,∵,,∴,在中,,,∴,
∴,故④正确.故选:C.
二.填空题(24分)
9.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 37 度.
第9题图 第10题图 第11题图 第12题图
10.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为 4 .
11.如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为 2或3 厘米/秒.
解:∵AB=AC,∴∠B=∠C,①当BD=CM=6厘米,BM=CN时,△DBM≌△MCN,
∴BM=CN=2厘米,t==1,∴点N运动的速度为2厘米/秒.②当BD=CN,BM=CM时,△DBM≌△NCM,∴BM=CM=4厘米,t==2,CN=BD=6厘米,∴点N的速度为:=3厘米/秒.故点N的速度为2或3厘米/秒.故答案为:2或3.
12.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
解:如图,取AB的中点E,连接CE,PE.∵∠ACB=90°,∠A=30°,∴∠CBE=60°,∵BE=AE,∴CE=BE=AE,∴△BCE是等边三角形,∴BC=BE,∵∠PBQ=∠CBE=60°,
∴∠QBC=∠PBE,∵QB=PB,CB=EB,∴△QBC≌△PBE(SAS),∴QC=PE,
∴当EP⊥AC时,QC的值最小,在Rt△AEP中,∵AE=,∠A=30°,∴PE=AE=,∴CQ的最小值为.
13.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是 10 cm.
解:底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为:×2π×=6(cm),展开得:
∵BC=8cm,AC=6cm,根据勾股定理得:AB==10(cm).故答案为:10.
第13题图 第14题图 第15题图 第16题图
14.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点,则BE的长为 .
解:由题意得:FC=BC=10,BE=EF(设为x);∵四边形ABCD为矩形,∴∠D=90°,DC=BC=8,
由勾股定理得:DF2=102﹣82=16,∴DF=4,AF=10﹣4=6;由勾股定理得:EF2=AE2+AF2,
即x2=(8﹣x)2+62解得:x=,故该题答案为.
15.如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
解:作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是BC边上的中线,∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,在Rt△ABD中,由勾股定理得:AD==12,∴S△ABC=×BC×AD=×AB×CN,∴CN===,∵E关于AD的对称点M,
∴EF=FM,∴CF+EF=CF+FM=CM,根据垂线段最短得出:CM≥CN,即CF+EF≥,
即CF+EF的最小值是,故答案为:.
如图,,点M、N分别在射线OA、OB上,MN=6,△OMN的面积为12,P是直线MN上的动点,点P关于OA对称的点为,点P关于OB对称的点为,当点P在直线NM上运动时,的面积最小值为___8___.
解:如图,连接,过点作交的延长线于,∵,且,∴,∵点关于对称的点为,点关于对称的点为,∴,,,∵,∴,∴的面积为,
由垂线段最短可知,当点与点重合时,取得最小值,最小值为,
∴的面积的最小值为,故答案为:8.
三.解答题(72分)
17.(6分)如图,方格纸上画有AB、CD两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法)
(1)请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;
(2)请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形,请画出所有
情形.
解:所作图形如图:
18.(8分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
解:(1)证明:∵∠BAC=∠DAE=90°∴∠BAC+∠CAD=∠DAE+CAD即∠BAD=∠CAE,
又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS).
(2)BD、CE特殊位置关系为BD⊥CE.证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.∵∠DAE=90°,∴∠E+∠ADE=90°.∴∠ADB+∠ADE=90°.即∠BDE=90°.∴BD、CE特殊位置关系为BD⊥CE.
19.(8分)如图,已知,DC∥AB,将BC边沿EF对折后,点B恰好落在CD边上B点处,点的对应点是C,
(1)求证:BF=B′F;
(2)求证:△EB′F是等腰三角形.
解:(1)证明:∵BC边沿EF对折后,点B恰好落在CD边上B′点处,点的对应点是C′,
∴FC=FC′,BC=B′C′,在△BCF和△B′C′F,,
∴△BCF≌△B′C′F,∴BF=B′F;
(2)∵BC边沿EF对折后,点B恰好落在CD边上B′点处,点的对应点是C′,∴∠BEF=∠B′EF,∵DC∥AB,∴∠B′FE=∠BEF,∴∠B′EF=∠B′FE,∴△EB′F是等腰三角形.
20.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长13cm,AC=6cm,求DC长.
解:(1)∵AD垂直平分BE,EF垂直平分AC,∴AB=AE=EC,∴∠C=∠CAE,
∵∠BAE=40°,∴∠AED=70°,∴∠C=∠AED=35°;(2)∵△ABC周长13cm,AC=6cm,
∴AB+BE+EC=7cm,即2DE+2EC=7cm,∴DE+EC=DC=3.5cm.
21.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
解:(1)结论:BD=EF+AG.理由:如图1中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,
∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,
∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,
同理可证:△BHC≌△AGB,∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
(2)结论不变.理由:如图2中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,同理可证:△BHC≌△AGB,
∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
22.(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
解:【定义】如图①,如图②所示,
【应用】(1)①如图③当∠B=42°,AD为“好线”,则AD=AD=BD,故这个三角形最大内角是∠C=84°;②如图④当∠B=42°,AD为“好线”,则AB=AD,AD=CD,这个三角形最大内角是∠BAC=103.5°;③如图⑤当∠ABC=42°时,BD为“好线”,
则AD=BD,CD=BC,故这个三角形最大内角是∠C=124°,④如图⑥,当∠B=42°时,CD为“好线”,则AD=CD=BC,故这个三角形最大内角是∠ACB=117°,⑤如图⑦,当∠B=42°时,CD为“好线”,则AD=AC,CD=BD,故这个三角形最大内角是∠ACB=126°,综上所述,这个三角形最大内角的所有可能值是84°或103.5°或124°或117°或126°,故答案为:84°或103.5°或124°或117°或126°;
(2)设∠B=x°,①当AD=DE时,如图1(a),∵AD=CD,∴∠C=∠CAD=27°,
∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠DAE=2x°,∴27×2+2x+x=180,∴x=42,
∴∠B=42°;②当AD=AE时,如图1(b),∵AD=CD,∴∠C=∠CAD=27°,∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠ADE=2x°,∴2x+x=27+27,∴x=18,∴∠B=18°.③当EA=DE时,∵90﹣x+27+27+x=180,∴x不存在,应舍去.综合上述:满足条件的x=42°或18°.
23.(12分)(1)阅读理解: 如图①,在△ABC中,若AB=8,AC=12,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,体现了转化和化归的数学思想,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DM⊥DN于点D,DM交AB于点M,DN交AC于点N,连接MN,求证:BM+CN>MN;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=110°,以C为顶点作一个55°角,角的两边分别交AB,AD于M、N两点,连接MN,探索线段BM,DN,MN之间的数量关系,并加以证明.
解:(1)阅读理解:延长AD到点E使DE=AD,再连接BE,∵AD是BC边上的中线,
∴BD=CD,在△ACD和△EBD中,∵,∴△ACD≌△EBD(SAS),
∴BE=AC=12,在△ABE中,由三角形的三边关系得:BE-AB<AE<BE+AB,
∴12-8<AE<12+8,即4<AE<20,∴2<AD<10;故答案为:2<AD<10;
(2)问题解决:证明:延长ND至点F,使FD=ND,连接BF、MF,如图1所示:
同(1)得:△BFD≌△CND(SAS),∴BF=CN,∵DM⊥DN,FD=ND,∴MF=MN,
在△BFM中,由三角形的三边关系得:BM+BF>MF,∴BM+CN>MN;
(3)问题拓展:解:BM+DN=MN;理由如下:延长AB至点E,使BE=DN,连接CE,如图2所示,∵∠ABC+∠D=180°,∠EBC+∠ABC=180°,∴∠EBC=∠D,在△EBC和△NDC中,∵,∴△EBC≌△NDC(SAS),∴CE=CN,∠ECB=∠NCD,∵∠BCD=110°,∠MCN=55°,∴∠BCM+∠NCD=55°,∴∠ECM=55°=∠MCN,在△NCM和△ECM中,
∵,∴△NCM≌△ECM(SAS),∴MN=ME,∵BM+BE=ME,∴BM+DN=MN.
24.(12分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
【小试牛刀】把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,S△EBC= ,S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
【知识运用】(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP 的距离.
解:【小试牛刀】S梯形ABCD=a(a+b),S△EBC=b(a﹣b),S四边形AECD=c2,
它们满足的关系式为: a(a+b)=b(a﹣b)+c2,答案为: a(a+b),b(a﹣b),c2, a(a+b)=b(a﹣b)+c2.
【知识运用】(1)如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,∴BC=AE,CE=AB,∴DE=AD﹣AE=25﹣16=9千米,
∴CD===41(千米),∴两个村庄相距41千米.故答案为:41.
(2)如图2②所示:设AP=x千米,则BP=(40﹣x)千米,在Rt△ADP中,DP2=AP2+AD2=x2+242,在Rt△BPC中,CP2=BP2+BC2=(40﹣x)2+162,∵PC=PD,
∴x2+242=(40﹣x)2+162,解得x=16,即AP=16千米.
(时间:100分钟 满分:120分)
一.选择题(24分)
1.在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
2.勾股定理是历史是第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B.C. D.
3.如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°则∠O的度数为( )
A.10° B.15° C.18° D.20°
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )
A.15cm B.13cm C.11cm D.9cm
5.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
6.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
A.3cm B.4cm C.5cm D.6cm
第6题图 第7题图 第8题图
7. 如图,点、分别是边长为的等边边、上的动点,点从顶点,点从顶点同时出发,且它们的速度都为,下面四个结论:①②≌③的度数不变,始终等于④当第秒或第秒时,为直角三角形,正确的有( )个.
A. B. C. D.
8.在中,,,、为上两点,,为外一点,且,,则下列结论:①;②;③;④,其中正确的是( )
A.①②③④ B.②③ C.①②④ D.①③④
二.填空题(24分)
9.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 度.
第9题图 第10题图 第11题图 第12题图
10.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为 .
11.如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为 厘米/秒.
12.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
13.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是 cm.
第13题图 第14题图 第15题图 第16题图
14.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点,则BE的长为 .
15.如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
16.如图,,点M、N分别在射线OA、OB上,MN=6,△OMN的面积为12,P是直线MN上的动点,点P关于OA对称的点为,点P关于OB对称的点为,当点P在直线NM上运动时,的面积最小值为______.
三.解答题(72分)
17.(6分)如图,方格纸上画有AB、CD两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法)
(1)请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;
(2)请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形,请画出所有
情形.
18.(8分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
19.(8分)如图,已知,DC∥AB,将BC边沿EF对折后,点B恰好落在CD边上B点处,点的对应点是C,
(1)求证:BF=B′F;
(2)求证:△EB′F是等腰三角形.
20.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长13cm,AC=6cm,求DC长.
21.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
22.(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
23.(12分)(1)阅读理解: 如图①,在△ABC中,若AB=8,AC=12,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,体现了转化和化归的数学思想,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DM⊥DN于点D,DM交AB于点M,DN交AC于点N,连接MN,求证:BM+CN>MN;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=110°,以C为顶点作一个55°角,角的两边分别交AB,AD于M、N两点,连接MN,探索线段BM,DN,MN之间的数量关系,并加以证明.
24.(12分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
【小试牛刀】把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,S△EBC= ,S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
【知识运用】(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP 的距离.
教师样卷
一.选择题(24分)
1.在下列各组条件中,不能说明△ABC≌△DEF的是( B )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
2.勾股定理是历史是第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( A )
A. B.C. D.
3.如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°则∠O的度数为( C )
A.10° B.15° C.18° D.20°
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( B )
A.15cm B.13cm C.11cm D.9cm
5.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( C )
A.1个 B.2个 C.3个 D.4个
6.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( C )
A.3cm B.4cm C.5cm D.6cm
第6题图 第7题图 第8题图
7. 如图,点、分别是边长为的等边边、上的动点,点从顶点,点从顶点同时出发,且它们的速度都为,下面四个结论:①②≌③的度数不变,始终等于④当第秒或第秒时,为直角三角形,正确的有( C )个.
A. B. C. D.
解:∵点、速度相同,∴.在和中,,
∴≌,故②正确.则.
.∴.则,故③正确.
∵不一定等于.∴.∴.故①错误.设时间为t,则AP=BQ=t,PB=4-t①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得6-t=2t,t=2 ;②当∠BPQ=90°时,
∵∠B=60°,∴BQ=2BP,得t=2(6-t),t=4;∴当第2秒或第4秒时,△PBQ为直角三角形.
∴④正确.故选C.
8.在中,,,、为上两点,,为外一点,且,,则下列结论:①;②;③;④,其中正确的是( C )
A.①②③④ B.②③ C.①②④ D.①③④
解:∵,,,∴,
,∴,∵,,
∴,∵,∴,∴,∴,故①正确;由①中证明,∴,∵,,∴,∴,连接,∵,∴,∵,,∴,故②正确;
设与的交点为,∵,,∴,,
∴,故③错误,∵,,∴,在中,,,∴,
∴,故④正确.故选:C.
二.填空题(24分)
9.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 37 度.
第9题图 第10题图 第11题图 第12题图
10.如图,已知AD∥BC,DE、CE分别平分∠ADC、∠DCB,AB过点E,且AB⊥AD,若AB=8,则点E到CD的距离为 4 .
11.如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为 2或3 厘米/秒.
解:∵AB=AC,∴∠B=∠C,①当BD=CM=6厘米,BM=CN时,△DBM≌△MCN,
∴BM=CN=2厘米,t==1,∴点N运动的速度为2厘米/秒.②当BD=CN,BM=CM时,△DBM≌△NCM,∴BM=CM=4厘米,t==2,CN=BD=6厘米,∴点N的速度为:=3厘米/秒.故点N的速度为2或3厘米/秒.故答案为:2或3.
12.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
解:如图,取AB的中点E,连接CE,PE.∵∠ACB=90°,∠A=30°,∴∠CBE=60°,∵BE=AE,∴CE=BE=AE,∴△BCE是等边三角形,∴BC=BE,∵∠PBQ=∠CBE=60°,
∴∠QBC=∠PBE,∵QB=PB,CB=EB,∴△QBC≌△PBE(SAS),∴QC=PE,
∴当EP⊥AC时,QC的值最小,在Rt△AEP中,∵AE=,∠A=30°,∴PE=AE=,∴CQ的最小值为.
13.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是 10 cm.
解:底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为:×2π×=6(cm),展开得:
∵BC=8cm,AC=6cm,根据勾股定理得:AB==10(cm).故答案为:10.
第13题图 第14题图 第15题图 第16题图
14.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点,则BE的长为 .
解:由题意得:FC=BC=10,BE=EF(设为x);∵四边形ABCD为矩形,∴∠D=90°,DC=BC=8,
由勾股定理得:DF2=102﹣82=16,∴DF=4,AF=10﹣4=6;由勾股定理得:EF2=AE2+AF2,
即x2=(8﹣x)2+62解得:x=,故该题答案为.
15.如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
解:作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是BC边上的中线,∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,在Rt△ABD中,由勾股定理得:AD==12,∴S△ABC=×BC×AD=×AB×CN,∴CN===,∵E关于AD的对称点M,
∴EF=FM,∴CF+EF=CF+FM=CM,根据垂线段最短得出:CM≥CN,即CF+EF≥,
即CF+EF的最小值是,故答案为:.
如图,,点M、N分别在射线OA、OB上,MN=6,△OMN的面积为12,P是直线MN上的动点,点P关于OA对称的点为,点P关于OB对称的点为,当点P在直线NM上运动时,的面积最小值为___8___.
解:如图,连接,过点作交的延长线于,∵,且,∴,∵点关于对称的点为,点关于对称的点为,∴,,,∵,∴,∴的面积为,
由垂线段最短可知,当点与点重合时,取得最小值,最小值为,
∴的面积的最小值为,故答案为:8.
三.解答题(72分)
17.(6分)如图,方格纸上画有AB、CD两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法)
(1)请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;
(2)请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形,请画出所有
情形.
解:所作图形如图:
18.(8分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
解:(1)证明:∵∠BAC=∠DAE=90°∴∠BAC+∠CAD=∠DAE+CAD即∠BAD=∠CAE,
又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS).
(2)BD、CE特殊位置关系为BD⊥CE.证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.∵∠DAE=90°,∴∠E+∠ADE=90°.∴∠ADB+∠ADE=90°.即∠BDE=90°.∴BD、CE特殊位置关系为BD⊥CE.
19.(8分)如图,已知,DC∥AB,将BC边沿EF对折后,点B恰好落在CD边上B点处,点的对应点是C,
(1)求证:BF=B′F;
(2)求证:△EB′F是等腰三角形.
解:(1)证明:∵BC边沿EF对折后,点B恰好落在CD边上B′点处,点的对应点是C′,
∴FC=FC′,BC=B′C′,在△BCF和△B′C′F,,
∴△BCF≌△B′C′F,∴BF=B′F;
(2)∵BC边沿EF对折后,点B恰好落在CD边上B′点处,点的对应点是C′,∴∠BEF=∠B′EF,∵DC∥AB,∴∠B′FE=∠BEF,∴∠B′EF=∠B′FE,∴△EB′F是等腰三角形.
20.(8分)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长13cm,AC=6cm,求DC长.
解:(1)∵AD垂直平分BE,EF垂直平分AC,∴AB=AE=EC,∴∠C=∠CAE,
∵∠BAE=40°,∴∠AED=70°,∴∠C=∠AED=35°;(2)∵△ABC周长13cm,AC=6cm,
∴AB+BE+EC=7cm,即2DE+2EC=7cm,∴DE+EC=DC=3.5cm.
21.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
解:(1)结论:BD=EF+AG.理由:如图1中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,
∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,
∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,
同理可证:△BHC≌△AGB,∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
(2)结论不变.理由:如图2中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,同理可证:△BHC≌△AGB,
∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
22.(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
解:【定义】如图①,如图②所示,
【应用】(1)①如图③当∠B=42°,AD为“好线”,则AD=AD=BD,故这个三角形最大内角是∠C=84°;②如图④当∠B=42°,AD为“好线”,则AB=AD,AD=CD,这个三角形最大内角是∠BAC=103.5°;③如图⑤当∠ABC=42°时,BD为“好线”,
则AD=BD,CD=BC,故这个三角形最大内角是∠C=124°,④如图⑥,当∠B=42°时,CD为“好线”,则AD=CD=BC,故这个三角形最大内角是∠ACB=117°,⑤如图⑦,当∠B=42°时,CD为“好线”,则AD=AC,CD=BD,故这个三角形最大内角是∠ACB=126°,综上所述,这个三角形最大内角的所有可能值是84°或103.5°或124°或117°或126°,故答案为:84°或103.5°或124°或117°或126°;
(2)设∠B=x°,①当AD=DE时,如图1(a),∵AD=CD,∴∠C=∠CAD=27°,
∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠DAE=2x°,∴27×2+2x+x=180,∴x=42,
∴∠B=42°;②当AD=AE时,如图1(b),∵AD=CD,∴∠C=∠CAD=27°,∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠ADE=2x°,∴2x+x=27+27,∴x=18,∴∠B=18°.③当EA=DE时,∵90﹣x+27+27+x=180,∴x不存在,应舍去.综合上述:满足条件的x=42°或18°.
23.(12分)(1)阅读理解: 如图①,在△ABC中,若AB=8,AC=12,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,体现了转化和化归的数学思想,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DM⊥DN于点D,DM交AB于点M,DN交AC于点N,连接MN,求证:BM+CN>MN;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=110°,以C为顶点作一个55°角,角的两边分别交AB,AD于M、N两点,连接MN,探索线段BM,DN,MN之间的数量关系,并加以证明.
解:(1)阅读理解:延长AD到点E使DE=AD,再连接BE,∵AD是BC边上的中线,
∴BD=CD,在△ACD和△EBD中,∵,∴△ACD≌△EBD(SAS),
∴BE=AC=12,在△ABE中,由三角形的三边关系得:BE-AB<AE<BE+AB,
∴12-8<AE<12+8,即4<AE<20,∴2<AD<10;故答案为:2<AD<10;
(2)问题解决:证明:延长ND至点F,使FD=ND,连接BF、MF,如图1所示:
同(1)得:△BFD≌△CND(SAS),∴BF=CN,∵DM⊥DN,FD=ND,∴MF=MN,
在△BFM中,由三角形的三边关系得:BM+BF>MF,∴BM+CN>MN;
(3)问题拓展:解:BM+DN=MN;理由如下:延长AB至点E,使BE=DN,连接CE,如图2所示,∵∠ABC+∠D=180°,∠EBC+∠ABC=180°,∴∠EBC=∠D,在△EBC和△NDC中,∵,∴△EBC≌△NDC(SAS),∴CE=CN,∠ECB=∠NCD,∵∠BCD=110°,∠MCN=55°,∴∠BCM+∠NCD=55°,∴∠ECM=55°=∠MCN,在△NCM和△ECM中,
∵,∴△NCM≌△ECM(SAS),∴MN=ME,∵BM+BE=ME,∴BM+DN=MN.
24.(12分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
【小试牛刀】把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,S△EBC= ,S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
【知识运用】(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP 的距离.
解:【小试牛刀】S梯形ABCD=a(a+b),S△EBC=b(a﹣b),S四边形AECD=c2,
它们满足的关系式为: a(a+b)=b(a﹣b)+c2,答案为: a(a+b),b(a﹣b),c2, a(a+b)=b(a﹣b)+c2.
【知识运用】(1)如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,∴BC=AE,CE=AB,∴DE=AD﹣AE=25﹣16=9千米,
∴CD===41(千米),∴两个村庄相距41千米.故答案为:41.
(2)如图2②所示:设AP=x千米,则BP=(40﹣x)千米,在Rt△ADP中,DP2=AP2+AD2=x2+242,在Rt△BPC中,CP2=BP2+BC2=(40﹣x)2+162,∵PC=PD,
∴x2+242=(40﹣x)2+162,解得x=16,即AP=16千米.
同课章节目录
