2.1 整式 同步练习(含答案) 2022—-2023学年上学期七年级数学期末试题选编
文档属性
| 名称 | 2.1 整式 同步练习(含答案) 2022—-2023学年上学期七年级数学期末试题选编 |

|
|
| 格式 | docx | ||
| 文件大小 | 262.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览



文档简介
2.1 整式 同步练习
一、单选题
1.(2022秋·吉林白城·七年级期末)一款羽绒服的成本价为a元,销售价比成本价增加了15%,现因库存积压,所以就按销售价的75%出售,那么这款羽绒服每件的实际售价为( )
A.(1+15%)(1+75%)a元 B.75%(1+15%)a元
C.(1+15%)(1-75%)a元 D.(1+15%+70%)a元
2.(2022秋·吉林长春·七年级期末)如图,用相同的小正方形按照某种规律进行摆放,则第9个图形中小正方形的个数是( )
A.98 B.100 C.109 D.110
3.(2022秋·吉林长春·七年级期末)下列代数式符合书写要求的是( )
A. B. C. D.
4.(2022秋·吉林·七年级期末)下列说法不正确的是( )
A.0是单项式 B.不是单项式
C.的系数是 D.是整式
5.(2022秋·吉林松原·七年级统考期末)下列说法错误的是( )
A.2x2-3xy-1是二次三项式 B.﹣x+1不是单项式
C.﹣的系数是﹣ D.﹣22xa3b2的次数是6
6.(2022秋·吉林长春·七年级期末)多项式﹣5xy+xy2﹣1是( )
A.二次三项式 B.三次三项式 C.四次三项式 D.五次三项式
二、填空题
7.(2022秋·吉林长春·七年级期末)兰兰同学买了铅笔支,每支元,买了练习本本,每本元,则她买铅笔和练习本一共花费了 元.
8.(2022秋·吉林松原·七年级统考期末)某商场对原单价为元的书包打8折出售,则该种书包的现在单价为 元.
9.(2022秋·吉林长春·七年级期末)某种商品每件的进价为m元,标价为n元,后来由于该商品积压,于是将此商品按标价的70%销售,则该商品每件利润为 元.
10.(2022秋·吉林·七年级统考期末)苹果进价是每千克x元,要得到20%的利润,则该苹果售价应是每千克 元(用含x的代数式表示).
11.(2022秋·吉林长春·七年级期末)某滑雪场在“元旦”期间推出特惠活动:票价每人140元,团体购票超过20人,票价可以享受八折优惠.活动期间,某旅游团有m(m>20)人来该滑雪场游玩,则应付票价总额为 元.
12.(2022秋·吉林·七年级期末)初一某班有m人,现抽其去参加女排训练,又有4人去打扫公共卫生,此时还剩下 人.
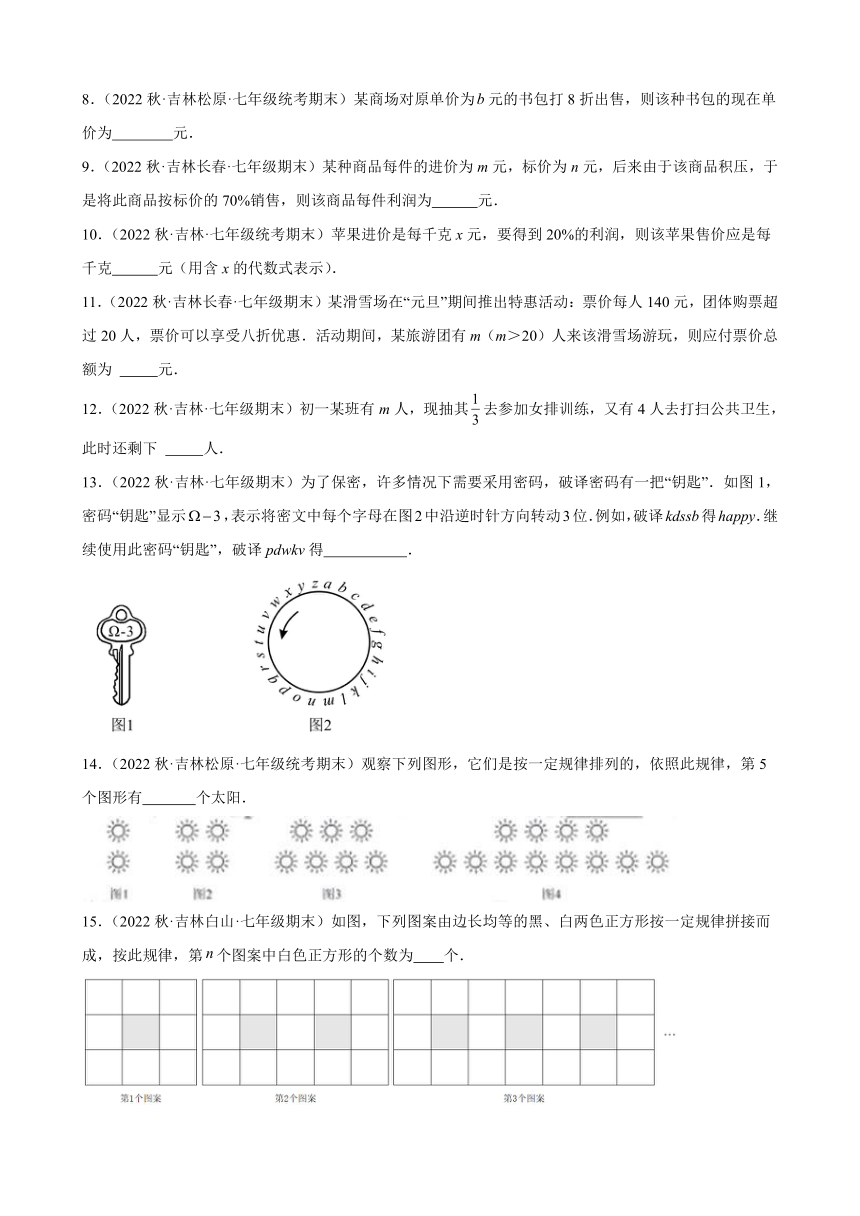
13.(2022秋·吉林·七年级期末)为了保密,许多情况下需要采用密码,破译密码有一把“钥匙”.如图1,密码“钥匙”显示,表示将密文中每个字母在图2中沿逆时针方向转动3位.例如,破译kdssb得happy.继续使用此密码“钥匙”,破译pdwkv得 .
14.(2022秋·吉林松原·七年级统考期末)观察下列图形,它们是按一定规律排列的,依照此规律,第5个图形有 个太阳.
15.(2022秋·吉林白山·七年级期末)如图,下列图案由边长均等的黑、白两色正方形按一定规律拼接而成,按此规律,第个图案中白色正方形的个数为 个.
16.(2022秋·吉林白城·七年级期末)单项式的系数是 .
17.(2022秋·吉林长春·七年级期末)单项式的次数是 .
18.(2022秋·吉林·七年级统考期末)是 次单项式.
19.(2022秋·吉林·七年级统考期末)单项式的系数与次数的和是 .
20.(2022秋·吉林长春·七年级期末)已知单项式﹣x2y2的系数为m,次数为n,则mn的值为 .
21.(2022秋·吉林白城·七年级统考期末)多项式是四次 项式
22.(2022秋·吉林·七年级统考期末)任意写出一个含有字母m,n的三次四项式,其中最高次项的系数为6,常数项为-8的式子为 .
23.(2022秋·吉林长春·七年级期末)若关于、的多项式是二次三项式,则 .
24.(2022秋·吉林长春·七年级期末)将多项式按字母降幂排列后,则从左边数第三项为 .
25.(2022秋·吉林长春·七年级期末)多项式x3﹣5xy2﹣7y3+8x2y按x的降幂排列为 .
26.(2022秋·吉林长春·七年级统考期末)定义一种新运算:“”观察下列各式:
,则 (用含a、b的代数式表示)
27.(2022秋·吉林·七年级统考期末)已知下列等式:
①13=12;
②13+23=32;
③13+23+33=62;
④13+23+33+43=102;
……
由此规律知,第⑤个等式是 .
28.(2022秋·吉林四平·七年级统考期末)探索与发现:下面是用分数(数字表示面积)砌成的“分数墙”,则整面“分数墙”的总面积是 .
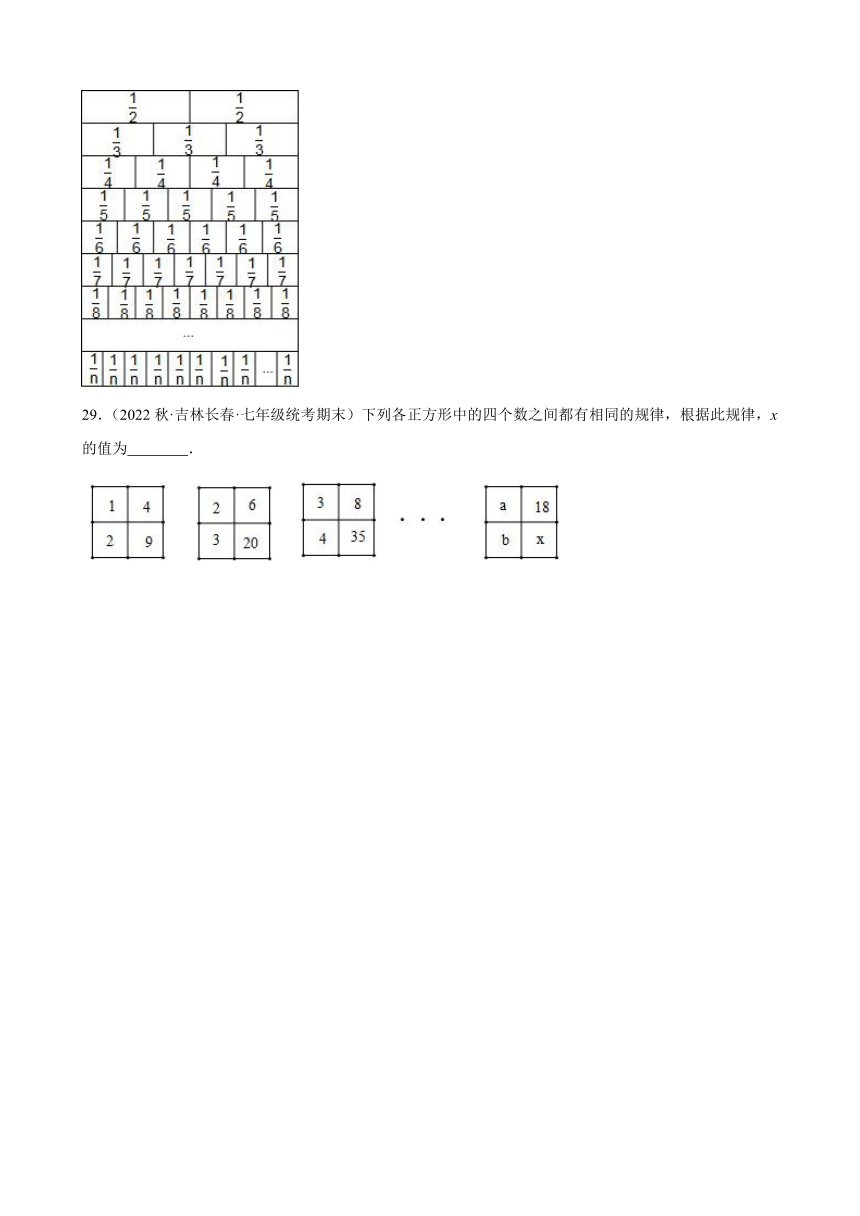
29.(2022秋·吉林长春·七年级统考期末)下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为 .
参考答案:
1.B
【分析】每台实际售价=成本价×(1+15%)×75%,根据等量关系直接列出代数式即可.
【详解】解:每台实际售价为75%(1+15%)a元,
故选:B.
【点睛】考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系,注意销售价比成本价增加15%后,再按销售价降价75%出售.
2.C
【分析】观察图形可知,第1个图形共有小正方形的个数为2×2+1;第2个图形共有小正方形的个数为3×3+2;第3个图形共有小正方形的个数为4×4+3;…;则第n个图形共有小正方形的个数为,把10代入计算,进而得出答案.
【详解】解:第1个图形共有小正方形的个数为2×2+1;
第2个图形共有小正方形的个数为3×3+2;
第3个图形共有小正方形的个数为4×4+3;
…;
则第n个图形共有小正方形的个数为,
所以第9个图形共有小正方形的个数为:10×10+9=109.
故选:C.
【点睛】本题考查了规律型:图形的变化类,解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.
3.C
【分析】根据代数式的表达方式,可得答案.
【详解】解:A、 ,不符合要求,故不符合题意;
B、系数应为假分数,故不符合题意;
C、符合要求,故符合题意;
D、应写成的形式,故不符合题意.
故选:C.
【点睛】本题考查了代数式,系数应为假分数,系数应写在字母的前面是解题关键.
4.B
【分析】字母或数字的乘积称作单项式,单独的数字或字母也是单项式,单项式中的数字因数是单项式的系数,几个单项式的和叫做多项式,单项式和多项式统称为整式,根据相关的知识点逐一判断即可.
【详解】解:A选项,0是单项式,故不符题意;
B选项,是单项式,故符合题意;
C选项,的系数是,故不符题意;
D选项,是整式,故不符题意.
故选:B.
【点睛】本题考查了单项式和多项式的相关概念,解决本题的关键是正确理解相关的概念.
5.C
【分析】根据单项式的个数就是多项式的项数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式,再结合单项式的次数与系数确定方法,进而得出答案.
【详解】解:A、2x2-3xy-1是二次二项式,正确,故此选项不合题意;
B、-x+1不是单项式,正确,故此选项不合题意;
C、的系数是,原说法错误,故此选项符合题意;
D、22xa3b2的次数是6,正确,故此选项不合题意;
故选:C.
【点睛】本题主要考查了多项式与单项式,正确掌握多项式的项数与次数确定方法是解题关键.
6.B
【分析】根据多项式的次数和项数的概念解答,多项式中次数最高项的次数是这个多项式的次数,每个单项式叫做多项式的项.
【详解】该多项式由,,这三项构成,其中的次数最高为3,因此,该多项式是三次三项式,故选B.
【点睛】本题考查了多项式的定义,理解掌握多项式项数定义及次数定义是解题关键.
7.
【分析】根据总花费买铅笔用的钱买练习本用的钱,列代数式即可得出答案.
【详解】解:∵兰兰同学买了铅笔支,每支元,买了练习本本,每本元,
∴买铅笔用的钱为:元,买练习本用的钱为:元,
∴她买铅笔和练习本一共花费了元.
故答案为:
【点睛】本题考查了列代数式,解本题的关键在明确题意,列出相应的代数式.
8.
【分析】根据售价=原售价×打折率列出代数式.
【详解】解:由题意知,该种书包的现在单价为0.8b.
故答案是:0.8b.
【点睛】此题考查列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系.
9.(0.7n-m)
【分析】根据利润=售价-进价列代数式求解即可.
【详解】解:根据题意,得0.7n-m.
所以该商品每件销售利润为(0.7n-m)元.
故答案为(0.7n-m).
【点睛】此题考查列代数式,正确理解题意,掌握列代数式的方法是解题的关键.
10.
【分析】根据售价=进价×(1+利润率)求解即可.
【详解】解:根据题意,售价=(1+20%)x=1.2x,
故答案为:1.2x.
【点睛】本题考查列代数式,熟知售价、进价和利润率的等量关系是解答的关键.
11.112m
【分析】根据题意,列出代数式化简即可得.
【详解】解:票价每人140元,团体购票超过20人,票价可以享受八折优惠,活动期间,某旅游团有m()人来该滑雪场游玩,
可得:,
故答案为:112m.
【点睛】题目主要考查列代数式,理解题意,列出代数式是解题关键.
12.
【分析】某班有人,抽其去参加女排训练,则抽去的人数为,用总人数减去女排训练的人数,再减去打扫卫生的人数,即为剩下的人数.
【详解】解:某班有人,现抽其去参加女排训练,
则抽去的人数为,
所以剩下的人数为:.
故答案为:.
【点睛】本题考查了根据实际问题列代数式,解题的关键是列代数式首先要弄清语句中各种数量的意义及其相互关系,然后把各种数量用适当的字母来表示,最后再把数及字母用适当的运算符号连接起来,从而列出代数式.
13.maths
【分析】根据题意和图示,直接找到pdwkv中的字母逆时针转动三位后的单词即可.
【详解】解:根据题意,pdwkv中的字母逆时针转动三位为:maths.
故答案为:maths.
【点睛】本题考查了材料阅读题,解决本题的关键是正确理解题意.
14.21
【详解】解:第一行的规律是1,2,3,4,…,故第五个数是5;第二行的规律是1,2,4,8,…,故第五个数是16;故第五个图中共有5+16=21个太阳.
故答案为:21.
【点睛】本题是规律题,数形结合思想解题,难度不大.
15./3+5n
【详解】解:第一个图中白色正方形的个数为:;
第二个图中白色正方形的个数为:;
第三个图中白色正方形的个数为:;
…
当其为第n个时,白色正方形的个数为:.
故答案为.
【点睛】本题考查规律型问题.
16.
【分析】根据单项式的系数:单项式中的数字因数,即可得出结果.
【详解】解:单项式的系数是:;
故答案为:.
【点睛】本题考查单项式的系数.熟练掌握单项式的系数是单项式中的数字因数,是解题的关键.
17.7
【分析】计算单项式中所有字母的指数和计算即可.
【详解】∵,
∴单项式的次数是7,
故答案为:7.
【点睛】本题考查了单项式的次数即单项式中所有字母的指数和,熟练掌握定义是解题的关键.
18.三/3
【分析】根据单项式的次数的定义即可求解.
【详解】解:单项式的次数是3,所以是三次单项式.
故答案为:三
【点睛】本题考查了单项式的次数,单项式的次数是指组成单项式的所有字母的指数和,熟知单项式的次数的定义是解题关键,注意几次单项式一般要用汉字,不用阿拉伯数字.
19.
【分析】单项式中的数字因数叫做这个单项式的系数,单项式中所有字母的指数的和叫做这个单项式的次数;由题意知单项式的系数与次数分别为-3,4,然后计算求解即可.
【详解】解:由题意知,单项式的系数与次数分别为-3,4
∵
∴系数与次数的和为1
故答案为:1.
【点睛】本题考查了单项式的系数与次数.解题的关键在于求出单项式的系数与次数.
20.﹣3.
【分析】直接利用单项式的次数与系数的定义分别得出m,n的值,即可得出答案.
【详解】解:∵单项式-x2y2的系数为m=-,次数为n=4,
∴mn的值为:-×4=-3.
故答案为-3.
【点睛】此题主要考查了单项式,正确把握单项式次数与系数的定义是解题关键.
21.五
【分析】根据几个单项式的和叫做多项式,其中每个单项式叫做多项式的项,即可求解.
【详解】解:多项式是四次五项式.
故答案为:五
【点睛】本题主要考查了多项式的项,熟练掌握几个单项式的和叫做多项式,其中每个单项式叫做多项式的项是解题的关键.
22.(答案不唯一)
【分析】根据题意,结合三次四项式、最高次项的系数为6,常数项可写出所求多项式,只要符合题意即可.
【详解】解:∵一个含有字母三次四项式,其中最高次项的系数为6,常数项为,
此多项式是:.
故答案是:.
【点睛】本题考查了列代数式,多项式,解题的关键是熟练掌握多项式中系数、最高次项、常数项的概念.
23.
【分析】直接利用多项式系数与次数确定方法得出 2m 1=0,进而得出答案.
【详解】解:∵关于x、y的多项式2x2+3mxy y2 xy 5是二次三项式,
∴3mxy xy=0,
则3m 1=0,
解得:m=.
故答案为:.
【点睛】此题主要考查了多项式,正确掌握相关定义是解题关键.
24.
【分析】先把多项式按照字母b的指数由高到低排列,从而可得答案.
【详解】解:多项式按字母降幂排列后为:
,
∴从左边数第三项为,
故答案为:.
【点睛】本题考查的是多项式的降幂排列,熟记多项式的降幂排列的含义是解本题的关键.
25.x3+8x2y﹣5xy2﹣7y3
【详解】多项式x3﹣5xy2﹣7y3+8x2y的各项为x3、﹣5xy2、﹣7y3、8x2y,
按x的降幂排列为:x3+8x2y﹣5xy2﹣7y3.
故答案为:x3+8x2y﹣5xy2﹣7y3.
26.3a+b
【分析】根据所给算式总结规律解答即可.
【详解】解:∵,
,
,
,
∴3a+b,
故答案为:3a+b.
【点睛】本题考查了规律型-数字的变化类,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
27.
【分析】根据题意,等式的左边为自然数的立方和,等式的右边为自然数的和的平方,据此规律即可求得第⑤个等式
【详解】①;
②;
③;
④;
……
由此规律知,第⑤个等式是
故答案为:
【点睛】本题考查了数字类找规律,找到等式右边的底数的规律是解题的关键.
28.n-1
【分析】由题意“分数墙”的总面积等于所有分数的和求解即可.
【详解】由题意“分数墙”的总面积,
故答案为.
【点睛】本题考查规律型问题,有理数的混合运算等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
29.170
【分析】由各正方形中的四个数之间的关系为第一行是
….;第一列为相邻的两个自然数,最后一个数是….;依此规律可进行求解.
【详解】解:由题意可得:
各正方形中的四个数之间的关系为第一行是….;第一列为相邻的两个自然数,最后一个数是….;
∴,,;
故答案为170.
【点睛】本题主要考查数字规律,关键是根据题意得到数字之间的规律,进而求解.
一、单选题
1.(2022秋·吉林白城·七年级期末)一款羽绒服的成本价为a元,销售价比成本价增加了15%,现因库存积压,所以就按销售价的75%出售,那么这款羽绒服每件的实际售价为( )
A.(1+15%)(1+75%)a元 B.75%(1+15%)a元
C.(1+15%)(1-75%)a元 D.(1+15%+70%)a元
2.(2022秋·吉林长春·七年级期末)如图,用相同的小正方形按照某种规律进行摆放,则第9个图形中小正方形的个数是( )
A.98 B.100 C.109 D.110
3.(2022秋·吉林长春·七年级期末)下列代数式符合书写要求的是( )
A. B. C. D.
4.(2022秋·吉林·七年级期末)下列说法不正确的是( )
A.0是单项式 B.不是单项式
C.的系数是 D.是整式
5.(2022秋·吉林松原·七年级统考期末)下列说法错误的是( )
A.2x2-3xy-1是二次三项式 B.﹣x+1不是单项式
C.﹣的系数是﹣ D.﹣22xa3b2的次数是6
6.(2022秋·吉林长春·七年级期末)多项式﹣5xy+xy2﹣1是( )
A.二次三项式 B.三次三项式 C.四次三项式 D.五次三项式
二、填空题
7.(2022秋·吉林长春·七年级期末)兰兰同学买了铅笔支,每支元,买了练习本本,每本元,则她买铅笔和练习本一共花费了 元.
8.(2022秋·吉林松原·七年级统考期末)某商场对原单价为元的书包打8折出售,则该种书包的现在单价为 元.
9.(2022秋·吉林长春·七年级期末)某种商品每件的进价为m元,标价为n元,后来由于该商品积压,于是将此商品按标价的70%销售,则该商品每件利润为 元.
10.(2022秋·吉林·七年级统考期末)苹果进价是每千克x元,要得到20%的利润,则该苹果售价应是每千克 元(用含x的代数式表示).
11.(2022秋·吉林长春·七年级期末)某滑雪场在“元旦”期间推出特惠活动:票价每人140元,团体购票超过20人,票价可以享受八折优惠.活动期间,某旅游团有m(m>20)人来该滑雪场游玩,则应付票价总额为 元.
12.(2022秋·吉林·七年级期末)初一某班有m人,现抽其去参加女排训练,又有4人去打扫公共卫生,此时还剩下 人.
13.(2022秋·吉林·七年级期末)为了保密,许多情况下需要采用密码,破译密码有一把“钥匙”.如图1,密码“钥匙”显示,表示将密文中每个字母在图2中沿逆时针方向转动3位.例如,破译kdssb得happy.继续使用此密码“钥匙”,破译pdwkv得 .
14.(2022秋·吉林松原·七年级统考期末)观察下列图形,它们是按一定规律排列的,依照此规律,第5个图形有 个太阳.
15.(2022秋·吉林白山·七年级期末)如图,下列图案由边长均等的黑、白两色正方形按一定规律拼接而成,按此规律,第个图案中白色正方形的个数为 个.
16.(2022秋·吉林白城·七年级期末)单项式的系数是 .
17.(2022秋·吉林长春·七年级期末)单项式的次数是 .
18.(2022秋·吉林·七年级统考期末)是 次单项式.
19.(2022秋·吉林·七年级统考期末)单项式的系数与次数的和是 .
20.(2022秋·吉林长春·七年级期末)已知单项式﹣x2y2的系数为m,次数为n,则mn的值为 .
21.(2022秋·吉林白城·七年级统考期末)多项式是四次 项式
22.(2022秋·吉林·七年级统考期末)任意写出一个含有字母m,n的三次四项式,其中最高次项的系数为6,常数项为-8的式子为 .
23.(2022秋·吉林长春·七年级期末)若关于、的多项式是二次三项式,则 .
24.(2022秋·吉林长春·七年级期末)将多项式按字母降幂排列后,则从左边数第三项为 .
25.(2022秋·吉林长春·七年级期末)多项式x3﹣5xy2﹣7y3+8x2y按x的降幂排列为 .
26.(2022秋·吉林长春·七年级统考期末)定义一种新运算:“”观察下列各式:
,则 (用含a、b的代数式表示)
27.(2022秋·吉林·七年级统考期末)已知下列等式:
①13=12;
②13+23=32;
③13+23+33=62;
④13+23+33+43=102;
……
由此规律知,第⑤个等式是 .
28.(2022秋·吉林四平·七年级统考期末)探索与发现:下面是用分数(数字表示面积)砌成的“分数墙”,则整面“分数墙”的总面积是 .
29.(2022秋·吉林长春·七年级统考期末)下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为 .
参考答案:
1.B
【分析】每台实际售价=成本价×(1+15%)×75%,根据等量关系直接列出代数式即可.
【详解】解:每台实际售价为75%(1+15%)a元,
故选:B.
【点睛】考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系,注意销售价比成本价增加15%后,再按销售价降价75%出售.
2.C
【分析】观察图形可知,第1个图形共有小正方形的个数为2×2+1;第2个图形共有小正方形的个数为3×3+2;第3个图形共有小正方形的个数为4×4+3;…;则第n个图形共有小正方形的个数为,把10代入计算,进而得出答案.
【详解】解:第1个图形共有小正方形的个数为2×2+1;
第2个图形共有小正方形的个数为3×3+2;
第3个图形共有小正方形的个数为4×4+3;
…;
则第n个图形共有小正方形的个数为,
所以第9个图形共有小正方形的个数为:10×10+9=109.
故选:C.
【点睛】本题考查了规律型:图形的变化类,解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.
3.C
【分析】根据代数式的表达方式,可得答案.
【详解】解:A、 ,不符合要求,故不符合题意;
B、系数应为假分数,故不符合题意;
C、符合要求,故符合题意;
D、应写成的形式,故不符合题意.
故选:C.
【点睛】本题考查了代数式,系数应为假分数,系数应写在字母的前面是解题关键.
4.B
【分析】字母或数字的乘积称作单项式,单独的数字或字母也是单项式,单项式中的数字因数是单项式的系数,几个单项式的和叫做多项式,单项式和多项式统称为整式,根据相关的知识点逐一判断即可.
【详解】解:A选项,0是单项式,故不符题意;
B选项,是单项式,故符合题意;
C选项,的系数是,故不符题意;
D选项,是整式,故不符题意.
故选:B.
【点睛】本题考查了单项式和多项式的相关概念,解决本题的关键是正确理解相关的概念.
5.C
【分析】根据单项式的个数就是多项式的项数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式,再结合单项式的次数与系数确定方法,进而得出答案.
【详解】解:A、2x2-3xy-1是二次二项式,正确,故此选项不合题意;
B、-x+1不是单项式,正确,故此选项不合题意;
C、的系数是,原说法错误,故此选项符合题意;
D、22xa3b2的次数是6,正确,故此选项不合题意;
故选:C.
【点睛】本题主要考查了多项式与单项式,正确掌握多项式的项数与次数确定方法是解题关键.
6.B
【分析】根据多项式的次数和项数的概念解答,多项式中次数最高项的次数是这个多项式的次数,每个单项式叫做多项式的项.
【详解】该多项式由,,这三项构成,其中的次数最高为3,因此,该多项式是三次三项式,故选B.
【点睛】本题考查了多项式的定义,理解掌握多项式项数定义及次数定义是解题关键.
7.
【分析】根据总花费买铅笔用的钱买练习本用的钱,列代数式即可得出答案.
【详解】解:∵兰兰同学买了铅笔支,每支元,买了练习本本,每本元,
∴买铅笔用的钱为:元,买练习本用的钱为:元,
∴她买铅笔和练习本一共花费了元.
故答案为:
【点睛】本题考查了列代数式,解本题的关键在明确题意,列出相应的代数式.
8.
【分析】根据售价=原售价×打折率列出代数式.
【详解】解:由题意知,该种书包的现在单价为0.8b.
故答案是:0.8b.
【点睛】此题考查列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系.
9.(0.7n-m)
【分析】根据利润=售价-进价列代数式求解即可.
【详解】解:根据题意,得0.7n-m.
所以该商品每件销售利润为(0.7n-m)元.
故答案为(0.7n-m).
【点睛】此题考查列代数式,正确理解题意,掌握列代数式的方法是解题的关键.
10.
【分析】根据售价=进价×(1+利润率)求解即可.
【详解】解:根据题意,售价=(1+20%)x=1.2x,
故答案为:1.2x.
【点睛】本题考查列代数式,熟知售价、进价和利润率的等量关系是解答的关键.
11.112m
【分析】根据题意,列出代数式化简即可得.
【详解】解:票价每人140元,团体购票超过20人,票价可以享受八折优惠,活动期间,某旅游团有m()人来该滑雪场游玩,
可得:,
故答案为:112m.
【点睛】题目主要考查列代数式,理解题意,列出代数式是解题关键.
12.
【分析】某班有人,抽其去参加女排训练,则抽去的人数为,用总人数减去女排训练的人数,再减去打扫卫生的人数,即为剩下的人数.
【详解】解:某班有人,现抽其去参加女排训练,
则抽去的人数为,
所以剩下的人数为:.
故答案为:.
【点睛】本题考查了根据实际问题列代数式,解题的关键是列代数式首先要弄清语句中各种数量的意义及其相互关系,然后把各种数量用适当的字母来表示,最后再把数及字母用适当的运算符号连接起来,从而列出代数式.
13.maths
【分析】根据题意和图示,直接找到pdwkv中的字母逆时针转动三位后的单词即可.
【详解】解:根据题意,pdwkv中的字母逆时针转动三位为:maths.
故答案为:maths.
【点睛】本题考查了材料阅读题,解决本题的关键是正确理解题意.
14.21
【详解】解:第一行的规律是1,2,3,4,…,故第五个数是5;第二行的规律是1,2,4,8,…,故第五个数是16;故第五个图中共有5+16=21个太阳.
故答案为:21.
【点睛】本题是规律题,数形结合思想解题,难度不大.
15./3+5n
【详解】解:第一个图中白色正方形的个数为:;
第二个图中白色正方形的个数为:;
第三个图中白色正方形的个数为:;
…
当其为第n个时,白色正方形的个数为:.
故答案为.
【点睛】本题考查规律型问题.
16.
【分析】根据单项式的系数:单项式中的数字因数,即可得出结果.
【详解】解:单项式的系数是:;
故答案为:.
【点睛】本题考查单项式的系数.熟练掌握单项式的系数是单项式中的数字因数,是解题的关键.
17.7
【分析】计算单项式中所有字母的指数和计算即可.
【详解】∵,
∴单项式的次数是7,
故答案为:7.
【点睛】本题考查了单项式的次数即单项式中所有字母的指数和,熟练掌握定义是解题的关键.
18.三/3
【分析】根据单项式的次数的定义即可求解.
【详解】解:单项式的次数是3,所以是三次单项式.
故答案为:三
【点睛】本题考查了单项式的次数,单项式的次数是指组成单项式的所有字母的指数和,熟知单项式的次数的定义是解题关键,注意几次单项式一般要用汉字,不用阿拉伯数字.
19.
【分析】单项式中的数字因数叫做这个单项式的系数,单项式中所有字母的指数的和叫做这个单项式的次数;由题意知单项式的系数与次数分别为-3,4,然后计算求解即可.
【详解】解:由题意知,单项式的系数与次数分别为-3,4
∵
∴系数与次数的和为1
故答案为:1.
【点睛】本题考查了单项式的系数与次数.解题的关键在于求出单项式的系数与次数.
20.﹣3.
【分析】直接利用单项式的次数与系数的定义分别得出m,n的值,即可得出答案.
【详解】解:∵单项式-x2y2的系数为m=-,次数为n=4,
∴mn的值为:-×4=-3.
故答案为-3.
【点睛】此题主要考查了单项式,正确把握单项式次数与系数的定义是解题关键.
21.五
【分析】根据几个单项式的和叫做多项式,其中每个单项式叫做多项式的项,即可求解.
【详解】解:多项式是四次五项式.
故答案为:五
【点睛】本题主要考查了多项式的项,熟练掌握几个单项式的和叫做多项式,其中每个单项式叫做多项式的项是解题的关键.
22.(答案不唯一)
【分析】根据题意,结合三次四项式、最高次项的系数为6,常数项可写出所求多项式,只要符合题意即可.
【详解】解:∵一个含有字母三次四项式,其中最高次项的系数为6,常数项为,
此多项式是:.
故答案是:.
【点睛】本题考查了列代数式,多项式,解题的关键是熟练掌握多项式中系数、最高次项、常数项的概念.
23.
【分析】直接利用多项式系数与次数确定方法得出 2m 1=0,进而得出答案.
【详解】解:∵关于x、y的多项式2x2+3mxy y2 xy 5是二次三项式,
∴3mxy xy=0,
则3m 1=0,
解得:m=.
故答案为:.
【点睛】此题主要考查了多项式,正确掌握相关定义是解题关键.
24.
【分析】先把多项式按照字母b的指数由高到低排列,从而可得答案.
【详解】解:多项式按字母降幂排列后为:
,
∴从左边数第三项为,
故答案为:.
【点睛】本题考查的是多项式的降幂排列,熟记多项式的降幂排列的含义是解本题的关键.
25.x3+8x2y﹣5xy2﹣7y3
【详解】多项式x3﹣5xy2﹣7y3+8x2y的各项为x3、﹣5xy2、﹣7y3、8x2y,
按x的降幂排列为:x3+8x2y﹣5xy2﹣7y3.
故答案为:x3+8x2y﹣5xy2﹣7y3.
26.3a+b
【分析】根据所给算式总结规律解答即可.
【详解】解:∵,
,
,
,
∴3a+b,
故答案为:3a+b.
【点睛】本题考查了规律型-数字的变化类,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
27.
【分析】根据题意,等式的左边为自然数的立方和,等式的右边为自然数的和的平方,据此规律即可求得第⑤个等式
【详解】①;
②;
③;
④;
……
由此规律知,第⑤个等式是
故答案为:
【点睛】本题考查了数字类找规律,找到等式右边的底数的规律是解题的关键.
28.n-1
【分析】由题意“分数墙”的总面积等于所有分数的和求解即可.
【详解】由题意“分数墙”的总面积,
故答案为.
【点睛】本题考查规律型问题,有理数的混合运算等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
29.170
【分析】由各正方形中的四个数之间的关系为第一行是
….;第一列为相邻的两个自然数,最后一个数是….;依此规律可进行求解.
【详解】解:由题意可得:
各正方形中的四个数之间的关系为第一行是….;第一列为相邻的两个自然数,最后一个数是….;
∴,,;
故答案为170.
【点睛】本题主要考查数字规律,关键是根据题意得到数字之间的规律,进而求解.
