数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 933.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
4.3.1 对数的概念
学习目标
问题1 求指数x
概念生成
对数的概念
问题3 对数的一般化定义
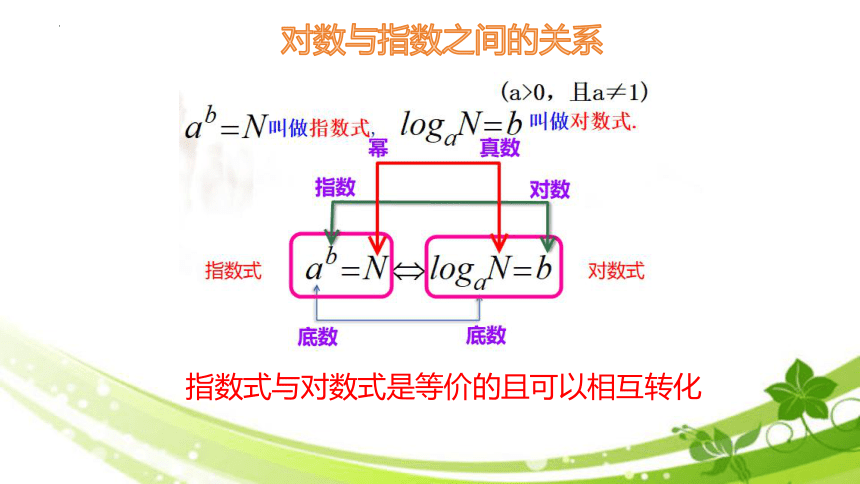
对数与指数之间的关系
指数式与对数式是等价的且可以相互转化
思考:下列数值存在吗?说明什么?
归纳小结
1、指数与对数之间的关系
2、对数的基本性质
3、对数恒等式
在生活中如充电器的电容电压关系,物体的自然冷却关系,细胞繁殖等,为了描述其自然规律,经常会用到无理数2.71828......用e表示这个无理数
1、求下列各式中x的值.
巩固练习
2、把下列指数式化为对数式,对数式化为指数式
3、求下列对数的值.
归纳小结
1理解对数的概念,掌握对数的性质,能进行简单的对数计算.
(重点、难点)
2.理解指数式与对数式的等价关系,会进行对数式与指数式的互化.
(重点)
3理解常用对数、自然对数的概念及记法.
对于形如a'=W(a>0且a≠1)求x的问题
1.1=2
那么x可以记作X=0g1,12,读作以1.1为底2的对数
2=3
那么x可以记作X=l0g23
,读作以2为底3的对数
若2=W呢
x=log2N
读作以2为底的对数
若am=N(a>0且a≠1)呢
x=log N
如果a"=W(a>0,a≠1),x=
x-=log≤一真数
底数
读作:以a为底,N的对数
(a>0,且a≠1)
a乃=Nm叫做指数式
og。V設叫破对数式
真数
指数
对数
指数式
N→logN=b
对数式
底数
底数
对数的重要结论
(1)负数和零没有对数
(2)loga1=0(a>0且a≠1)
a0=1
(3)1oga=1(a>0且a≠1)
←al=a
典例2①若loga2=m,loga3=n,其中a>0且a≠1,则am+”=
②
将以下指数式与对数式进行互化.
(1)5
2
5
(2)1o824
(3)1g0.001=-3
(1)1og6g=-
2
(2)1088=6
(3)lg100=x
(4)-lne2=x
(5)1og2(1ogx9)=1
(6)1og7[log3(log2]=0
(1)54=625
(2)2-6=
64
(3)(3)
=5.73
(4)1og116=-4
2
(5)1g0.01=-2
(6)1n10=2.303
对数的定义
指对数的关系
常用对数
两个特殊的对数°
自然对数
小结
e
log,a=1
三个常用结论
log:1=0
ogaN
a
=N
4.3.1 对数的概念
学习目标
问题1 求指数x
概念生成
对数的概念
问题3 对数的一般化定义
对数与指数之间的关系
指数式与对数式是等价的且可以相互转化
思考:下列数值存在吗?说明什么?
归纳小结
1、指数与对数之间的关系
2、对数的基本性质
3、对数恒等式
在生活中如充电器的电容电压关系,物体的自然冷却关系,细胞繁殖等,为了描述其自然规律,经常会用到无理数2.71828......用e表示这个无理数
1、求下列各式中x的值.
巩固练习
2、把下列指数式化为对数式,对数式化为指数式
3、求下列对数的值.
归纳小结
1理解对数的概念,掌握对数的性质,能进行简单的对数计算.
(重点、难点)
2.理解指数式与对数式的等价关系,会进行对数式与指数式的互化.
(重点)
3理解常用对数、自然对数的概念及记法.
对于形如a'=W(a>0且a≠1)求x的问题
1.1=2
那么x可以记作X=0g1,12,读作以1.1为底2的对数
2=3
那么x可以记作X=l0g23
,读作以2为底3的对数
若2=W呢
x=log2N
读作以2为底的对数
若am=N(a>0且a≠1)呢
x=log N
如果a"=W(a>0,a≠1),x=
x-=log≤一真数
底数
读作:以a为底,N的对数
(a>0,且a≠1)
a乃=Nm叫做指数式
og。V設叫破对数式
真数
指数
对数
指数式
N→logN=b
对数式
底数
底数
对数的重要结论
(1)负数和零没有对数
(2)loga1=0(a>0且a≠1)
a0=1
(3)1oga=1(a>0且a≠1)
←al=a
典例2①若loga2=m,loga3=n,其中a>0且a≠1,则am+”=
②
将以下指数式与对数式进行互化.
(1)5
2
5
(2)1o824
(3)1g0.001=-3
(1)1og6g=-
2
(2)1088=6
(3)lg100=x
(4)-lne2=x
(5)1og2(1ogx9)=1
(6)1og7[log3(log2]=0
(1)54=625
(2)2-6=
64
(3)(3)
=5.73
(4)1og116=-4
2
(5)1g0.01=-2
(6)1n10=2.303
对数的定义
指对数的关系
常用对数
两个特殊的对数°
自然对数
小结
e
log,a=1
三个常用结论
log:1=0
ogaN
a
=N
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
