数学人教A版(2019)选择性必修第二册4.1.2数列中的递推关系 课件(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.1.2数列中的递推关系 课件(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1001.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-06 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第四章 数列
4.1.2 数列中的递推关系
一、课题导入
什么是通项公式?通项公式有什么作用?
如果数列{an}的第n项与序号之间的关系可以用一个公式来表示,那么这个公式就叫做数列的通项公式.
如数列0,1,2,3......的通项公式为
an=n-1
二、引导探究1——数列的递推关系
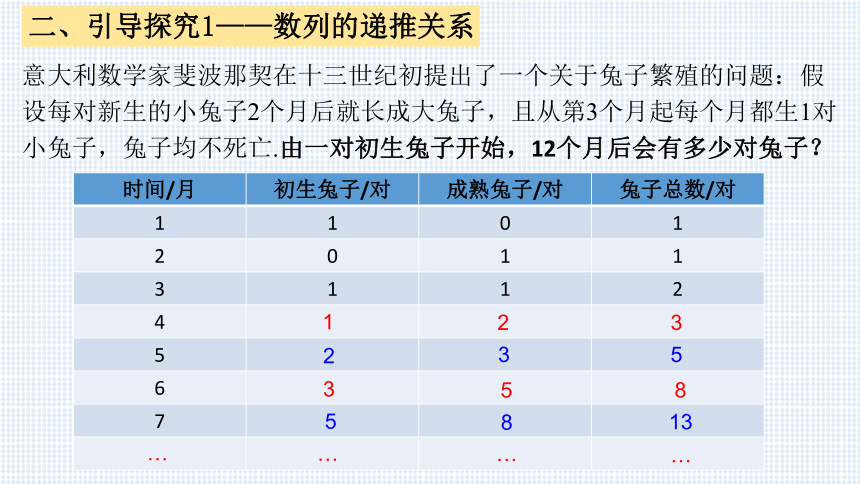
意大利数学家斐波那契在十三世纪初提出了一个关于兔子繁殖的问题:假设每对新生的小兔子2个月后就长成大兔子,且从第3个月起每个月都生1对小兔子,兔子均不死亡.由一对初生兔子开始,12个月后会有多少对兔子?
时间/月 初生兔子/对 成熟兔子/对 兔子总数/对
1 1 0 1
2 0 1 1
3 1 1 2
4
5
6
7
1
13
8
5
8
5
3
5
2
3
2
3
…
…
…
…
从第1个月开始,以后每个月的兔子总对数是
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ….
你发现这个数列的规律了吗?
由1对新生的小兔子开始,记每个月的兔子对数构成的数列为 .
如果用Fn表示第n个月的兔子的总对数,数列的规律是递推关系: Fn=Fn-1+Fn-2(n>2)
这个数列称为斐波那契数列.
所以,过了一年之后,总共会有233对兔子.
定义:如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
递推公式
通项公式
项与序号之间的关系
相邻两项之间的关系
(n≥2)
知道了首项和递推公式,就能求出数列的每一项了.
:1,3,9,27,….
n=1,
,
,
n≥2.
1.数列的递推公式
区别
两者都能确定一个数列
联系
二、引导探究2——数列的前n项和
定义:我们把数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn,,即
Sn =a1+a2+...+an
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
思考:数列的前n项和公式与数列的通项公式有何联系?
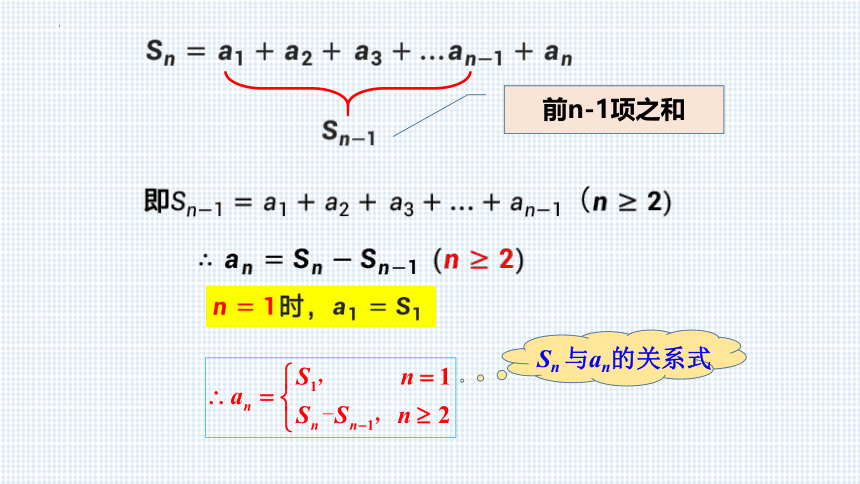
前n-1项之和
Sn 与an的关系式
三、典型例题1 根据递推关系求数列中的项
三、典型例题2 周期性数列
A
三、典型例题3 由数列的递推公式求通项公式
方法总结
三、典型例题4 由数列前n项和公式求通项数列
方法总结
1.递推公式:(1)初始值;(2)递推关系式
已知数列的递推公式,求前几项并猜出通项公式
3.用递推公式求数列通项公式的方法:观察法、累加法、累乘法.
四、课堂小结
第四章 数列
4.1.2 数列中的递推关系
一、课题导入
什么是通项公式?通项公式有什么作用?
如果数列{an}的第n项与序号之间的关系可以用一个公式来表示,那么这个公式就叫做数列的通项公式.
如数列0,1,2,3......的通项公式为
an=n-1
二、引导探究1——数列的递推关系
意大利数学家斐波那契在十三世纪初提出了一个关于兔子繁殖的问题:假设每对新生的小兔子2个月后就长成大兔子,且从第3个月起每个月都生1对小兔子,兔子均不死亡.由一对初生兔子开始,12个月后会有多少对兔子?
时间/月 初生兔子/对 成熟兔子/对 兔子总数/对
1 1 0 1
2 0 1 1
3 1 1 2
4
5
6
7
1
13
8
5
8
5
3
5
2
3
2
3
…
…
…
…
从第1个月开始,以后每个月的兔子总对数是
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ….
你发现这个数列的规律了吗?
由1对新生的小兔子开始,记每个月的兔子对数构成的数列为 .
如果用Fn表示第n个月的兔子的总对数,数列的规律是递推关系: Fn=Fn-1+Fn-2(n>2)
这个数列称为斐波那契数列.
所以,过了一年之后,总共会有233对兔子.
定义:如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
递推公式
通项公式
项与序号之间的关系
相邻两项之间的关系
(n≥2)
知道了首项和递推公式,就能求出数列的每一项了.
:1,3,9,27,….
n=1,
,
,
n≥2.
1.数列的递推公式
区别
两者都能确定一个数列
联系
二、引导探究2——数列的前n项和
定义:我们把数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn,,即
Sn =a1+a2+...+an
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
思考:数列的前n项和公式与数列的通项公式有何联系?
前n-1项之和
Sn 与an的关系式
三、典型例题1 根据递推关系求数列中的项
三、典型例题2 周期性数列
A
三、典型例题3 由数列的递推公式求通项公式
方法总结
三、典型例题4 由数列前n项和公式求通项数列
方法总结
1.递推公式:(1)初始值;(2)递推关系式
已知数列的递推公式,求前几项并猜出通项公式
3.用递推公式求数列通项公式的方法:观察法、累加法、累乘法.
四、课堂小结
