第二十四章 圆 复习小结第2课时(考点强化) 课件(共40张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 第二十四章 圆 复习小结第2课时(考点强化) 课件(共40张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览











文档简介
考点强化
第二十四章 圆
| 小结与复习 第2课时 |
考点一 圆的有关的概念
1.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
B
一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是(? )
A.2.5 cm或6.5 cm B.2.5 cm C.6.5 cm D.5 cm或13cm
A
考点二 垂径定理及推论
A
如图,AB 为 ⊙O 的直径,弦 CD⊥AB 于点 E,OC = 5,CD = 8,则 AE 的长 ( )
A. 8 cm B. 5 cm C. 3 cm D. 2 cm
如图,CD 为 ⊙O 的直径,弦 AB⊥CD 于 E,OE = 12,AB = 10,求直径 CD 的长.
解:如图,连接 OA.
∵AB⊥CD,CD 过圆心 O,AB = 10,
∴AE = BE = 5,∠AEO = 90°.
在 Rt△AEO 中,由勾股定理得:
∴CD = 2AO = 26.
如图,∠C = 90°,以 AC 为半径的圆 C 与 AB 交于点 D .若 AC = 3,CB = 4,求 BD 的长.
解:如图,过点 C 作 CE ⊥ AB 于 E,
则 AE = DE,在 Rt△ACB 中,
E
考点三 弧、弦、圆心角关系
如图,AB是⊙O的直径,BC=CD=DE,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
?
A
考点四 圆周定理及推论
如图已知四边形 ABCD 内接于 ⊙O ,∠A =100°,则 ∠BOD = ( )
A. 80° B. 50° C. 160° D. 100°
C
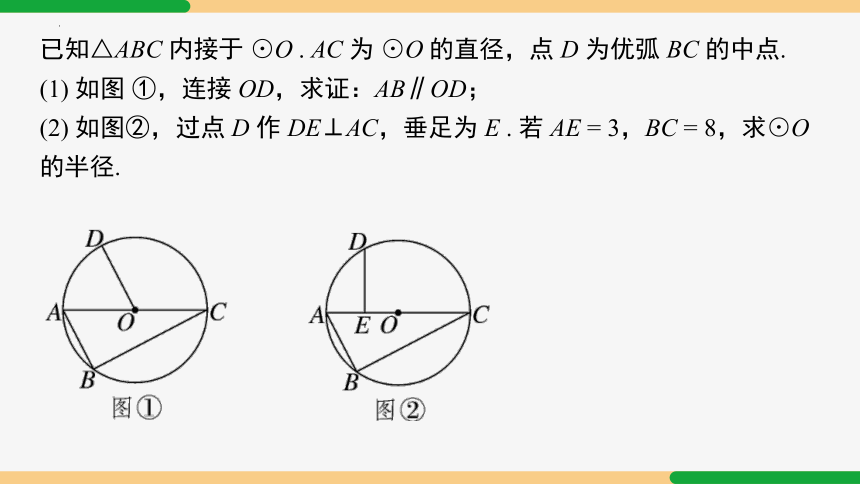
已知△ABC 内接于 ⊙O . AC 为 ⊙O 的直径,点 D 为优弧 BC 的中点.
(1) 如图 ①,连接 OD,求证:AB∥OD;
(2) 如图②,过点 D 作 DE⊥AC,垂足为 E . 若 AE = 3,BC = 8,求⊙O 的半径.
(1) 证明:如图 ①,延长 DO 交 BC 于 F.
∵ 点 D 为优弧 BC 的中点,
∴ .
∴ DF⊥BC.
∵ AC 为 ⊙O 的直径,
∴ AB⊥BC.
∴ AB∥OD.
F
(2)解:如图 ②,连接 DO 并延长交 BC 于 F.
∵点 D 为优弧 BC 的中点,
∴
∴ DF⊥CB.
∵DE ⊥AC,∠DEO = ∠OFC = 90°.
∵∠DOE = ∠COF,OD = OC,
∴△DOE≌△DOE(AAS).
F
∴ OF = OE = OA - 3.
∵ OC2 = OF2 + CF2,
∴ OC2 = (OC - 3)2 + 42.
∴ OC = .
∴ ⊙O 的半径为 .
考点五 切线的判定和性质
O
C
A
B
E
D
50
如图,线段 AB 是直径,点 D 是 ☉O 上一点, ∠CDB = 20°,过点 C 作 ☉O 的切线交 AB 的延长线于点 E,则 ∠E 等于 °.
如图,PA 与⊙O 相切于点 A,过点 A 作 AB⊥OP,垂足为 C,交⊙O 于点 B.连接 PB,AO,并延长 AO 交⊙O 于点 D,与 PB 的延长线交于点 E.
(1) 求证:PB 是⊙O 的切线;
(2) 若 AP = 5,PE = 13,求 DE 的长.
A
B
D
C
O
E
P
(1) 求证:PB 是⊙O 的切线;
证明:连接 OB.
∵ PO⊥AB,
∴ AC = BC.
∴ PA = PB.
∵ PO = PO,
∴△PAO≌△PBO (SSS).
∴∠OAP =∠OBP.
∵ PA 是⊙O 的切线,
∴∠OAP = 90°.
∴∠OBP = 90°.
∴ PB 是⊙O 的切线.
A
B
D
C
O
E
P
(2) 若 AP = 5,PE = 13,求 DE 的长.
解:在 Rt△APE 中,
由勾股定理易得 AE = 12.
由 (1) 知 AP = BP = 5,则 BE = 8.
∵ PB 为⊙O 的切线,∴∠OBE = 90°.
设 OB = r,则 OE = 12 - r.
在 Rt△OBE 中,由勾股定理得
r2 + 82 = (12 - r)2,
A
B
D
C
O
E
P
解得 r = .
考点六 与圆有关的计算
如图所示的网格中,每个小正方形的边长均为 1,点 A,B,D 均在小正方形的顶点上,且点 B,C 在 弧 AD 上,∠BAC = 22.5°,则 弧 BC 的长为____.
如图,在等腰 △ABC 中,∠BAC=120°,AD 是∠BAC 的平分线,且 AD = 6,以点 A 为圆心,AD长为半径画弧 EF,交 AB 于点 E,交 AC 于点 F.
(1)求图中阴影部分的面积;
(2) 将阴影部分剪掉,余下扇形 AEF,将扇形AEF 围成一个圆锥的侧面,AE 与 AF 正好重合,圆锥侧面无重叠,求这个圆锥的高 h.
解:(1) 在等腰 △ABC 中,∠BAC=120°
∴∠B = 30°.
∵ AD 是 ∠BAC 的平分线,
∴ AD⊥BC,BD = CD.
∴ AB = 2AD =12. ∴BD= .
(1)求图中阴影部分的面积;
(2) 将阴影部分剪掉,余下扇形 AEF,将扇形AEF 围成一个圆锥的侧面,AE 与 AF 正好重合,圆锥侧面无重叠,求这个圆锥的高 h.
(2) 根据题意得:
这个圆锥的高
考点训练
矩形 OABC 的边 OA,OC 分别在 x 轴、y 轴的正半轴上,点 D 在 OA 的延长线上,以O 为圆心、OD 长为半径的弧经过点 B 交 y 轴正半轴于点E.连接 DEBE 若 A(2,0),∠BED = 30°,则 CE 的长是____________.
1. 平面直角坐标系中,M 点坐标为 (-2,3),以 2 为半径画⊙M,则以下结论正确的是( )
A.⊙M 与 x 轴相交,与 y 轴相切
B.⊙M 与 x 轴相切,与 y 轴相离
C.⊙M 与 x 轴相离,与 y 轴相交
D.⊙M 与 x 轴相离,与 y 轴相切
D
如图,BD是⊙O的直径,点A,C在⊙O上,AB=AD,AC交BD于点G.若∠COD=126°.则∠AGB的度数为(????)
A.99° B.108° C.110° D.117°
?
B
如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠ABD=54°,则∠C的度数为(?? ??)
A.34° B.36° C.46° D.54°
?
B
如图,在△ABC中,∠C=90°,AB=4,以C点为圆心,2为半径作⊙C,则AB的中点O与⊙C的位置关系是( )
A.点O在⊙C外 B.点O在⊙C上
C.点O在⊙C内 D.不能确定
B
如图,平面直角坐标系中,⊙????与????轴分别交于????、????两点,点????的坐标为3,?1,????????=23.将⊙????沿着与????轴平行的方向平移多少距离时⊙????与????轴相切 (?? ?)
A.1 B.2 C.3 D.1或3
?
D
如图,在????????????????????????中,∠????=90°,????????=4,????????=3,以点????为圆心,3为半径的圆与????????所在直线的位置关系是( ??)
A.相交 B.相离 C.相切 D.无法判断
?
B
如图,等边三角形????????????的边长为8,以????????上一点????为圆心的圆分别与边????????,????????相切,则⊙????的半径为( )
A.23 B.3 C.4 D.4?3
?
【详解】设⊙????与????????的切点为????,连接????????,????????,
∵等边三角形????????????的边长为8,∴????????=8,∠????=∠????????????=60°,
∵圆分别与边????????,????????相切,∴∠????????????=∠????????????=12∠????????????=30°
∴∠????????????=90°∴????????=12????????=4,
∵????????⊥????????,∴????????=32????????=23,
∴⊙????的半径为23,
故选A.
?
A
如图,AB是⊙????的直径,PA与⊙????相切于点A,BC//OP交⊙????于点C.若∠????=70°,则∠????????????的度数为(???? )
A.10° B.20° C.30° D.40°
?
【详解】
如图,连接OC,因为OB=OC,所以∠OCB=∠OBC=70°,
所以∠BOC=180°-70°-70°=40°,
又因为BC//OP,所以∠AOP=∠B=70°,
∴∠POC=180°-∠AOP-∠BOC=70°,所以在△PAO和△PCO中,????????=????????∠????????????=∠????????????????????=????????,所以△PAO≌△PCO(SAS),
所以∠OCP=∠OAP,因为PA与⊙????相切于点A,所以∠OCP=∠OAP=90°,
所以∠OPC=180°-∠POC-∠OCP=20°,故选:B.
?
B
若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A.2 B.22?2?????? C.2?2 D.2—1
?
【详解】解:∵等腰直角三角形外接圆半径为2,
∴此直角三角形的斜边长为4,两条直角边分别为22,
∴它的内切圆半径为:R=12(22+22-4)=22-2.
故选:B.
?
B
如图,在?????????????????中,∠????=60°,⊙????的半径为3,则图中阴影部分的面积是(??)
A.???? B.2???? C.3???? D.6????
?
【详解】
∵在?ABCD中,∠B=60°,⊙C的半径为3,
∴∠C=120°,
∴图中阴影部分的面积是:120×????×32360=3π,
故选C.
?
某几何体的三视图及相关数据(单位:cm)如图所示,则该几何体的侧面积是(????)
A.65????2????????2 B.60????????????2 C.65????????????2 D.130????????????2
?
【详解】解:由三视图可判断出该几何体为圆锥,圆锥的高为12cm,底部圆的半径为5cm,
∴圆锥母线长为:????=52+122=13cm,
又∵????圆锥侧=??????????????,将R=5cm,????=13cm代入,
∴????圆锥侧=??????????????=65????(????????2),
故选:C.
?
如图,在△ABC中,AB=AC,点D在AC边上,过△ABD的内心I作IE⊥BD于点E.若BD=10,CD=4,则BE的长为(????)
A.6 B.7 C.8 D.9
【详解】解:如图,过点????作????????⊥????????,????????⊥????????,
∵????是△????????????的内心,∴????????=????????,????????=????????,????????=????????,
设????????=????????=????,????????=????????=????,
∵BD=10,∴????????=????????=10?????,
∴????????=????????+????????=????+10?????,????????=????????+????????=????+????+4,
∵????????=????????,
∴????+10?????=????+????+4,
解得????=3,
∴????????=?????????????????=10?3=7,
故选B.
?
如图,四边形????????????????是⊙????的内接四边形.若∠????????????=121°,则∠????????????的度数为(????)
A.138° B.121° C.118° D.112°
?
【详解】解:∵四边形ABCD内接于圆O,
∴∠????+∠????=180°
∵∠????????????=121°
∴∠????=59°
∴∠????????????=2∠????=118°
故选:C
?
【详解】解:连接OC、OD、OE,如图所示:
∵正六边形????????????????????????内接于⊙????,
∴∠COD= 3606=60°,则∠COE=120°,
∴∠CME= 12∠COE=60°,
故选:D.
?
如图,正六边形????????????????????????内接于⊙????,点M在????????上,则∠????????????的度数为(????)
A.30° B.36° C.45° D.60°
?
一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为__________.
【详解】解:连接AC,
∵∠ABC=90°,且∠ABC是圆周角,
∴AC是圆形镜面的直径,
由勾股定理得:AC= 13 cm,
所以圆形镜面的半径为132cm,
故答案为:132cm.
?
如图,在正六边形????????????????????????中,连接????????,????????,则∠????????????=____________度.
?
【详解】连接BE,交CF与点O,连接OA,
∵在正六边形????????????????????????中,
∴∠????????????=360°6=60°,
∵????????=????????
∴∠????????????=∠????????????
∵∠????????????=∠????????????+∠????????????=2∠????????????
∴∠????????????=30°,
故答案为:30.
?
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π)________.
【详解】解:设切点分别为D、E、F,连接OD、OE、OF,
∵⊙O为Rt△ABC的内切圆,
∴AE=AF、BD=BF、CD=CE,OD⊥BC,OE⊥AC,
∵∠C=90°,∴四边形CDOE为正方形,
∴∠EOF+∠FOD=360°-90°=270°,
设⊙O的半径为x,则CD=CE=x,AE=AF=4-x,BD=BF=3-x,
∴4-x+3-x=5,解得x=1,
∴S阴影=S△ABC-( S扇形EOF+ S扇形DOF)- S正方形CDOE=12×3×4-270????×12360?×1×1=5-3????4.
故答案为:5-3????4.
?
如图所示,已知三角形????????????为直角三角形,∠????????????=90°,DE为⊙????切线,????为切点,CA=CD,则△????????????和△????????????面积之比为(????)
A.1:3 B.1:2 C.2:2 D.2?1:1
?
(1)证明:如图,连接 OE,OF,
过点 O 作 OD⊥AB 于点 D.
∵ BC 与⊙O 相切于点 E.
∴ OE⊥BC.
∵ BO 是∠ABC 的平分线,∴ OD = OE.
∴ OD 是圆的一条半径.
∴ AB 是 ⊙O 的切线.
如图,在 Rt△ABC 中 ∠ACB = 90°,⊙O 与 BC,AC 分别相切于点 E,F,BO 平分∠ABC,连接 OA.
(1)求证:AB 是 ⊙O 的切线;
(2) 若 BE = AC = 3,⊙O 的半径是 1,求图中阴影部分的面积.
解:∵ BC、AC 与圆分别相切于点 E、 点 F.
∴ OE⊥BC,OF⊥AC.
又∵∠ACB = 90°,OE = OF,
∴ 四边形 OECF 是正方形.
∴ OE = OF = EC = FC = 1.
∴ BC = BE + EC = 4.
(2) 若 BE = AC = 3,⊙O 的半径是 1,求图中阴影部分的面积.
又∵ AC = 3.
∴
第二十四章 圆
| 小结与复习 第2课时 |
考点一 圆的有关的概念
1.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
B
一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是(? )
A.2.5 cm或6.5 cm B.2.5 cm C.6.5 cm D.5 cm或13cm
A
考点二 垂径定理及推论
A
如图,AB 为 ⊙O 的直径,弦 CD⊥AB 于点 E,OC = 5,CD = 8,则 AE 的长 ( )
A. 8 cm B. 5 cm C. 3 cm D. 2 cm
如图,CD 为 ⊙O 的直径,弦 AB⊥CD 于 E,OE = 12,AB = 10,求直径 CD 的长.
解:如图,连接 OA.
∵AB⊥CD,CD 过圆心 O,AB = 10,
∴AE = BE = 5,∠AEO = 90°.
在 Rt△AEO 中,由勾股定理得:
∴CD = 2AO = 26.
如图,∠C = 90°,以 AC 为半径的圆 C 与 AB 交于点 D .若 AC = 3,CB = 4,求 BD 的长.
解:如图,过点 C 作 CE ⊥ AB 于 E,
则 AE = DE,在 Rt△ACB 中,
E
考点三 弧、弦、圆心角关系
如图,AB是⊙O的直径,BC=CD=DE,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
?
A
考点四 圆周定理及推论
如图已知四边形 ABCD 内接于 ⊙O ,∠A =100°,则 ∠BOD = ( )
A. 80° B. 50° C. 160° D. 100°
C
已知△ABC 内接于 ⊙O . AC 为 ⊙O 的直径,点 D 为优弧 BC 的中点.
(1) 如图 ①,连接 OD,求证:AB∥OD;
(2) 如图②,过点 D 作 DE⊥AC,垂足为 E . 若 AE = 3,BC = 8,求⊙O 的半径.
(1) 证明:如图 ①,延长 DO 交 BC 于 F.
∵ 点 D 为优弧 BC 的中点,
∴ .
∴ DF⊥BC.
∵ AC 为 ⊙O 的直径,
∴ AB⊥BC.
∴ AB∥OD.
F
(2)解:如图 ②,连接 DO 并延长交 BC 于 F.
∵点 D 为优弧 BC 的中点,
∴
∴ DF⊥CB.
∵DE ⊥AC,∠DEO = ∠OFC = 90°.
∵∠DOE = ∠COF,OD = OC,
∴△DOE≌△DOE(AAS).
F
∴ OF = OE = OA - 3.
∵ OC2 = OF2 + CF2,
∴ OC2 = (OC - 3)2 + 42.
∴ OC = .
∴ ⊙O 的半径为 .
考点五 切线的判定和性质
O
C
A
B
E
D
50
如图,线段 AB 是直径,点 D 是 ☉O 上一点, ∠CDB = 20°,过点 C 作 ☉O 的切线交 AB 的延长线于点 E,则 ∠E 等于 °.
如图,PA 与⊙O 相切于点 A,过点 A 作 AB⊥OP,垂足为 C,交⊙O 于点 B.连接 PB,AO,并延长 AO 交⊙O 于点 D,与 PB 的延长线交于点 E.
(1) 求证:PB 是⊙O 的切线;
(2) 若 AP = 5,PE = 13,求 DE 的长.
A
B
D
C
O
E
P
(1) 求证:PB 是⊙O 的切线;
证明:连接 OB.
∵ PO⊥AB,
∴ AC = BC.
∴ PA = PB.
∵ PO = PO,
∴△PAO≌△PBO (SSS).
∴∠OAP =∠OBP.
∵ PA 是⊙O 的切线,
∴∠OAP = 90°.
∴∠OBP = 90°.
∴ PB 是⊙O 的切线.
A
B
D
C
O
E
P
(2) 若 AP = 5,PE = 13,求 DE 的长.
解:在 Rt△APE 中,
由勾股定理易得 AE = 12.
由 (1) 知 AP = BP = 5,则 BE = 8.
∵ PB 为⊙O 的切线,∴∠OBE = 90°.
设 OB = r,则 OE = 12 - r.
在 Rt△OBE 中,由勾股定理得
r2 + 82 = (12 - r)2,
A
B
D
C
O
E
P
解得 r = .
考点六 与圆有关的计算
如图所示的网格中,每个小正方形的边长均为 1,点 A,B,D 均在小正方形的顶点上,且点 B,C 在 弧 AD 上,∠BAC = 22.5°,则 弧 BC 的长为____.
如图,在等腰 △ABC 中,∠BAC=120°,AD 是∠BAC 的平分线,且 AD = 6,以点 A 为圆心,AD长为半径画弧 EF,交 AB 于点 E,交 AC 于点 F.
(1)求图中阴影部分的面积;
(2) 将阴影部分剪掉,余下扇形 AEF,将扇形AEF 围成一个圆锥的侧面,AE 与 AF 正好重合,圆锥侧面无重叠,求这个圆锥的高 h.
解:(1) 在等腰 △ABC 中,∠BAC=120°
∴∠B = 30°.
∵ AD 是 ∠BAC 的平分线,
∴ AD⊥BC,BD = CD.
∴ AB = 2AD =12. ∴BD= .
(1)求图中阴影部分的面积;
(2) 将阴影部分剪掉,余下扇形 AEF,将扇形AEF 围成一个圆锥的侧面,AE 与 AF 正好重合,圆锥侧面无重叠,求这个圆锥的高 h.
(2) 根据题意得:
这个圆锥的高
考点训练
矩形 OABC 的边 OA,OC 分别在 x 轴、y 轴的正半轴上,点 D 在 OA 的延长线上,以O 为圆心、OD 长为半径的弧经过点 B 交 y 轴正半轴于点E.连接 DEBE 若 A(2,0),∠BED = 30°,则 CE 的长是____________.
1. 平面直角坐标系中,M 点坐标为 (-2,3),以 2 为半径画⊙M,则以下结论正确的是( )
A.⊙M 与 x 轴相交,与 y 轴相切
B.⊙M 与 x 轴相切,与 y 轴相离
C.⊙M 与 x 轴相离,与 y 轴相交
D.⊙M 与 x 轴相离,与 y 轴相切
D
如图,BD是⊙O的直径,点A,C在⊙O上,AB=AD,AC交BD于点G.若∠COD=126°.则∠AGB的度数为(????)
A.99° B.108° C.110° D.117°
?
B
如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠ABD=54°,则∠C的度数为(?? ??)
A.34° B.36° C.46° D.54°
?
B
如图,在△ABC中,∠C=90°,AB=4,以C点为圆心,2为半径作⊙C,则AB的中点O与⊙C的位置关系是( )
A.点O在⊙C外 B.点O在⊙C上
C.点O在⊙C内 D.不能确定
B
如图,平面直角坐标系中,⊙????与????轴分别交于????、????两点,点????的坐标为3,?1,????????=23.将⊙????沿着与????轴平行的方向平移多少距离时⊙????与????轴相切 (?? ?)
A.1 B.2 C.3 D.1或3
?
D
如图,在????????????????????????中,∠????=90°,????????=4,????????=3,以点????为圆心,3为半径的圆与????????所在直线的位置关系是( ??)
A.相交 B.相离 C.相切 D.无法判断
?
B
如图,等边三角形????????????的边长为8,以????????上一点????为圆心的圆分别与边????????,????????相切,则⊙????的半径为( )
A.23 B.3 C.4 D.4?3
?
【详解】设⊙????与????????的切点为????,连接????????,????????,
∵等边三角形????????????的边长为8,∴????????=8,∠????=∠????????????=60°,
∵圆分别与边????????,????????相切,∴∠????????????=∠????????????=12∠????????????=30°
∴∠????????????=90°∴????????=12????????=4,
∵????????⊥????????,∴????????=32????????=23,
∴⊙????的半径为23,
故选A.
?
A
如图,AB是⊙????的直径,PA与⊙????相切于点A,BC//OP交⊙????于点C.若∠????=70°,则∠????????????的度数为(???? )
A.10° B.20° C.30° D.40°
?
【详解】
如图,连接OC,因为OB=OC,所以∠OCB=∠OBC=70°,
所以∠BOC=180°-70°-70°=40°,
又因为BC//OP,所以∠AOP=∠B=70°,
∴∠POC=180°-∠AOP-∠BOC=70°,所以在△PAO和△PCO中,????????=????????∠????????????=∠????????????????????=????????,所以△PAO≌△PCO(SAS),
所以∠OCP=∠OAP,因为PA与⊙????相切于点A,所以∠OCP=∠OAP=90°,
所以∠OPC=180°-∠POC-∠OCP=20°,故选:B.
?
B
若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A.2 B.22?2?????? C.2?2 D.2—1
?
【详解】解:∵等腰直角三角形外接圆半径为2,
∴此直角三角形的斜边长为4,两条直角边分别为22,
∴它的内切圆半径为:R=12(22+22-4)=22-2.
故选:B.
?
B
如图,在?????????????????中,∠????=60°,⊙????的半径为3,则图中阴影部分的面积是(??)
A.???? B.2???? C.3???? D.6????
?
【详解】
∵在?ABCD中,∠B=60°,⊙C的半径为3,
∴∠C=120°,
∴图中阴影部分的面积是:120×????×32360=3π,
故选C.
?
某几何体的三视图及相关数据(单位:cm)如图所示,则该几何体的侧面积是(????)
A.65????2????????2 B.60????????????2 C.65????????????2 D.130????????????2
?
【详解】解:由三视图可判断出该几何体为圆锥,圆锥的高为12cm,底部圆的半径为5cm,
∴圆锥母线长为:????=52+122=13cm,
又∵????圆锥侧=??????????????,将R=5cm,????=13cm代入,
∴????圆锥侧=??????????????=65????(????????2),
故选:C.
?
如图,在△ABC中,AB=AC,点D在AC边上,过△ABD的内心I作IE⊥BD于点E.若BD=10,CD=4,则BE的长为(????)
A.6 B.7 C.8 D.9
【详解】解:如图,过点????作????????⊥????????,????????⊥????????,
∵????是△????????????的内心,∴????????=????????,????????=????????,????????=????????,
设????????=????????=????,????????=????????=????,
∵BD=10,∴????????=????????=10?????,
∴????????=????????+????????=????+10?????,????????=????????+????????=????+????+4,
∵????????=????????,
∴????+10?????=????+????+4,
解得????=3,
∴????????=?????????????????=10?3=7,
故选B.
?
如图,四边形????????????????是⊙????的内接四边形.若∠????????????=121°,则∠????????????的度数为(????)
A.138° B.121° C.118° D.112°
?
【详解】解:∵四边形ABCD内接于圆O,
∴∠????+∠????=180°
∵∠????????????=121°
∴∠????=59°
∴∠????????????=2∠????=118°
故选:C
?
【详解】解:连接OC、OD、OE,如图所示:
∵正六边形????????????????????????内接于⊙????,
∴∠COD= 3606=60°,则∠COE=120°,
∴∠CME= 12∠COE=60°,
故选:D.
?
如图,正六边形????????????????????????内接于⊙????,点M在????????上,则∠????????????的度数为(????)
A.30° B.36° C.45° D.60°
?
一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为__________.
【详解】解:连接AC,
∵∠ABC=90°,且∠ABC是圆周角,
∴AC是圆形镜面的直径,
由勾股定理得:AC= 13 cm,
所以圆形镜面的半径为132cm,
故答案为:132cm.
?
如图,在正六边形????????????????????????中,连接????????,????????,则∠????????????=____________度.
?
【详解】连接BE,交CF与点O,连接OA,
∵在正六边形????????????????????????中,
∴∠????????????=360°6=60°,
∵????????=????????
∴∠????????????=∠????????????
∵∠????????????=∠????????????+∠????????????=2∠????????????
∴∠????????????=30°,
故答案为:30.
?
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π)________.
【详解】解:设切点分别为D、E、F,连接OD、OE、OF,
∵⊙O为Rt△ABC的内切圆,
∴AE=AF、BD=BF、CD=CE,OD⊥BC,OE⊥AC,
∵∠C=90°,∴四边形CDOE为正方形,
∴∠EOF+∠FOD=360°-90°=270°,
设⊙O的半径为x,则CD=CE=x,AE=AF=4-x,BD=BF=3-x,
∴4-x+3-x=5,解得x=1,
∴S阴影=S△ABC-( S扇形EOF+ S扇形DOF)- S正方形CDOE=12×3×4-270????×12360?×1×1=5-3????4.
故答案为:5-3????4.
?
如图所示,已知三角形????????????为直角三角形,∠????????????=90°,DE为⊙????切线,????为切点,CA=CD,则△????????????和△????????????面积之比为(????)
A.1:3 B.1:2 C.2:2 D.2?1:1
?
(1)证明:如图,连接 OE,OF,
过点 O 作 OD⊥AB 于点 D.
∵ BC 与⊙O 相切于点 E.
∴ OE⊥BC.
∵ BO 是∠ABC 的平分线,∴ OD = OE.
∴ OD 是圆的一条半径.
∴ AB 是 ⊙O 的切线.
如图,在 Rt△ABC 中 ∠ACB = 90°,⊙O 与 BC,AC 分别相切于点 E,F,BO 平分∠ABC,连接 OA.
(1)求证:AB 是 ⊙O 的切线;
(2) 若 BE = AC = 3,⊙O 的半径是 1,求图中阴影部分的面积.
解:∵ BC、AC 与圆分别相切于点 E、 点 F.
∴ OE⊥BC,OF⊥AC.
又∵∠ACB = 90°,OE = OF,
∴ 四边形 OECF 是正方形.
∴ OE = OF = EC = FC = 1.
∴ BC = BE + EC = 4.
(2) 若 BE = AC = 3,⊙O 的半径是 1,求图中阴影部分的面积.
又∵ AC = 3.
∴
同课章节目录
