24.2.1 点和圆位置关系 (第2课时反证法) 课件(共14张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 24.2.1 点和圆位置关系 (第2课时反证法) 课件(共14张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 25.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览




文档简介
反证法
24.2 点和圆、直线和圆的位置关系
| 24.2.1 点和圆的位置关系 第2课时 |
课堂导航
了解的反证法的基本思路和步骤
巩固点与圆的位置关系相关知识
知识回顾
点和圆的位置关系
点和圆的位置关系
确定圆的条件
点在圆外?d>r
点在圆内?d点在圆上?d=r
不在同一直线三点
三角形的外接圆心
三角形外心性质
·
r
C
O
A
B
新知探究
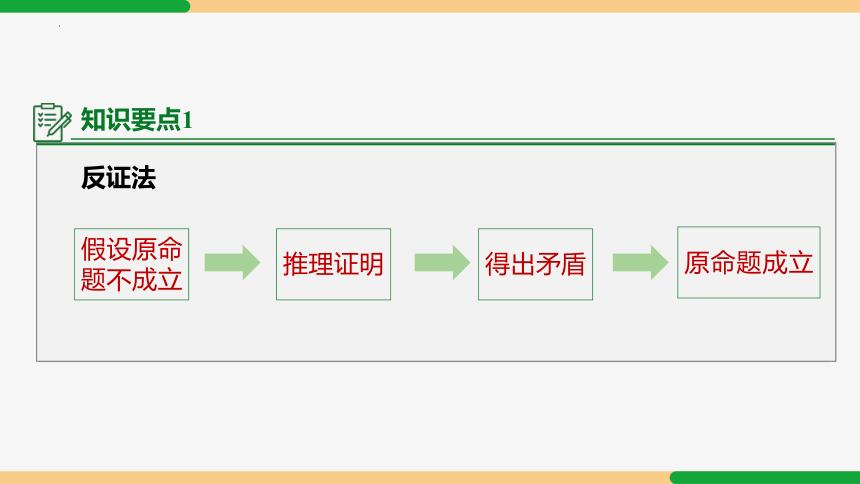
活动一 1.过同一平面内三个点作圆,情况会怎样呢?说说理由
D
E
G
F
●
O
A
B
C
圆心在三条线段垂直平分线的交点上.
l1
l2
A
B
C
l
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到 A、B、C 三点的距离都相等,
即圆心是线段 AB、BC 垂直平分线的交点.
分别作 AB、BC 垂直平分线 l1、l2.
显然 l1∥l2,
l1 与 l2 无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
l1
l2
A
B
C
P
l
知识要点1
反证法
假设原命题不成立
推理证明
得出矛盾
原命题成立
典例讲解
例1 求证:在一个三角形中,至少有一个内角≤60°.
已知:△ABC.
求证:△ABC 中至少有一个内角小于或等于 60°.
假设△ABC 中没有一个内角小于或等于 60°
则 ∠A > 60°,∠B > 60°,∠C > 60°
即 ∠A +∠B +∠C > 180°
这与三角形的内角和为 180°矛盾,故假设不成立
∴△ABC中至少有一个内角小于或等于 60°
∴∠A +∠B +∠C > 60° + 60° + 60° = 180°
例1 如图,在△ABC 中,O 是它的外心,BC = 24 cm,O 到 BC 的距离是 5 cm,求△ABC 的外接圆的半径.
解:连接 OB,过点 O 作 OD⊥BC 于点 D.
D
则 OD = 5 cm,
在 Rt△OBD 中,
即△ABC 的外接圆的半径为 13 cm.
课堂小结
·
r
C
O
A
B
点和圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:不在同一直线上的三个点可确定一个圆
一个三角形的
外接圆是唯一的
反证法
课堂练习
1.⊙O 的半径 r 为 5 cm,O 为原点,点 P 的坐标为(3,4), 则点 P 与⊙O 的位置关系为 ( )
A. 点 P 在⊙O 内 B. 点 P 在⊙O 上
C. 点 P 在⊙O 外 D. 点 P 在⊙O 上或⊙O 外
B
若⊙O的半径是5 cm,点A在⊙O内,则OA的长可能是( )
A.2 cm B.5 cm
C.6 cm D.10 cm
用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是 ( )
A.点在圆内 B.点在圆上
C.点在圆心上 D.点在圆上或圆内
A
D
如图,点O是△ABC的外心,∠A=70°,则∠BOC的度数是________.
140°
某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘要确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.
A
B
C
解:(1) 在圆形瓷盘的边缘选 A、B、C 三点;
(2) 连接 AB、BC;
(3) 分别作出 AB、BC 的垂直平分线;
(4) 两垂直平分线的交点就是瓷盘的圆心.
如图,已知 Rt△ABC 中 ,∠C = 90°,若 AC = 12 cm, BC = 5 cm,求△ABC 的外接圆半径.
C
B
A
O
解:设 Rt△ABC 的斜边 AB 的中点为 O,连接 OC,则 OA = OB = OC.
故点 O 是△ABC 的外心.
∵∠C = 90°,AC = 12 cm,BC = 5 cm,
∴ AB = 13 cm. 则 OA = 6.5 cm,
即 △ABC 的外接圆半径为 6.5 cm.
24.2 点和圆、直线和圆的位置关系
| 24.2.1 点和圆的位置关系 第2课时 |
课堂导航
了解的反证法的基本思路和步骤
巩固点与圆的位置关系相关知识
知识回顾
点和圆的位置关系
点和圆的位置关系
确定圆的条件
点在圆外?d>r
点在圆内?d
不在同一直线三点
三角形的外接圆心
三角形外心性质
·
r
C
O
A
B
新知探究
活动一 1.过同一平面内三个点作圆,情况会怎样呢?说说理由
D
E
G
F
●
O
A
B
C
圆心在三条线段垂直平分线的交点上.
l1
l2
A
B
C
l
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到 A、B、C 三点的距离都相等,
即圆心是线段 AB、BC 垂直平分线的交点.
分别作 AB、BC 垂直平分线 l1、l2.
显然 l1∥l2,
l1 与 l2 无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
l1
l2
A
B
C
P
l
知识要点1
反证法
假设原命题不成立
推理证明
得出矛盾
原命题成立
典例讲解
例1 求证:在一个三角形中,至少有一个内角≤60°.
已知:△ABC.
求证:△ABC 中至少有一个内角小于或等于 60°.
假设△ABC 中没有一个内角小于或等于 60°
则 ∠A > 60°,∠B > 60°,∠C > 60°
即 ∠A +∠B +∠C > 180°
这与三角形的内角和为 180°矛盾,故假设不成立
∴△ABC中至少有一个内角小于或等于 60°
∴∠A +∠B +∠C > 60° + 60° + 60° = 180°
例1 如图,在△ABC 中,O 是它的外心,BC = 24 cm,O 到 BC 的距离是 5 cm,求△ABC 的外接圆的半径.
解:连接 OB,过点 O 作 OD⊥BC 于点 D.
D
则 OD = 5 cm,
在 Rt△OBD 中,
即△ABC 的外接圆的半径为 13 cm.
课堂小结
·
r
C
O
A
B
点和圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:不在同一直线上的三个点可确定一个圆
一个三角形的
外接圆是唯一的
反证法
课堂练习
1.⊙O 的半径 r 为 5 cm,O 为原点,点 P 的坐标为(3,4), 则点 P 与⊙O 的位置关系为 ( )
A. 点 P 在⊙O 内 B. 点 P 在⊙O 上
C. 点 P 在⊙O 外 D. 点 P 在⊙O 上或⊙O 外
B
若⊙O的半径是5 cm,点A在⊙O内,则OA的长可能是( )
A.2 cm B.5 cm
C.6 cm D.10 cm
用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是 ( )
A.点在圆内 B.点在圆上
C.点在圆心上 D.点在圆上或圆内
A
D
如图,点O是△ABC的外心,∠A=70°,则∠BOC的度数是________.
140°
某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘要确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.
A
B
C
解:(1) 在圆形瓷盘的边缘选 A、B、C 三点;
(2) 连接 AB、BC;
(3) 分别作出 AB、BC 的垂直平分线;
(4) 两垂直平分线的交点就是瓷盘的圆心.
如图,已知 Rt△ABC 中 ,∠C = 90°,若 AC = 12 cm, BC = 5 cm,求△ABC 的外接圆半径.
C
B
A
O
解:设 Rt△ABC 的斜边 AB 的中点为 O,连接 OC,则 OA = OB = OC.
故点 O 是△ABC 的外心.
∵∠C = 90°,AC = 12 cm,BC = 5 cm,
∴ AB = 13 cm. 则 OA = 6.5 cm,
即 △ABC 的外接圆半径为 6.5 cm.
同课章节目录
