第二十四章 圆 复习小结第1课时(知识结构) 课件(共32张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 第二十四章 圆 复习小结第1课时(知识结构) 课件(共32张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览




文档简介
(共32张PPT)
知识结构与考点
第二十四章 圆
| 小结与复习 第1课时 |
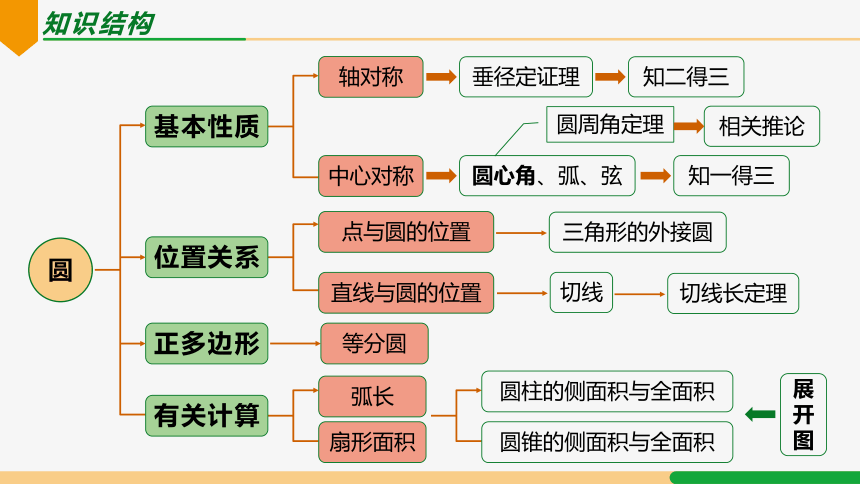
知识结构
圆
垂径定证理
轴对称
中心对称
知二得三
圆心角、弧、弦
知一得三
圆周角定理
相关推论
点与圆的位置
直线与圆的位置
三角形的外接圆
切线
切线长定理
弧长
扇形面积
等分圆
圆柱的侧面积与全面积
圆锥的侧面积与全面积
展开图
基本性质
位置关系
正多边形
有关计算
一 圆的有关的性质
(一) 圆的有关的概念
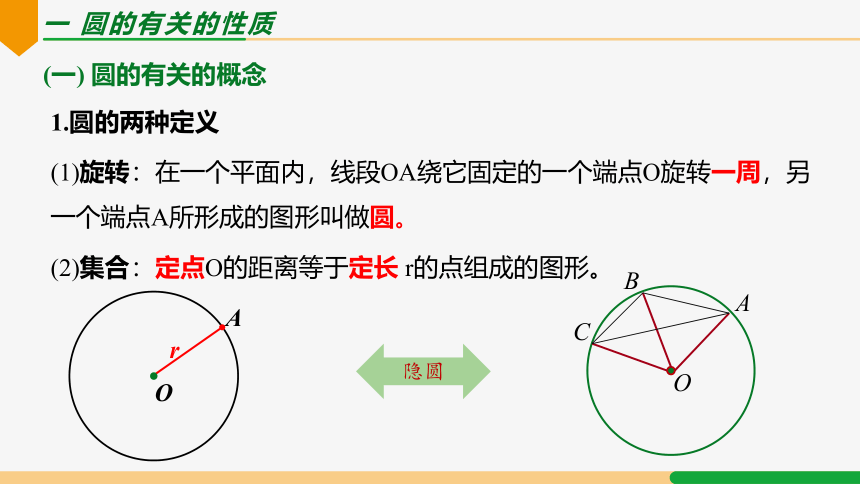
1.圆的两种定义
(1)旋转:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。
O
r
A
(2)集合:定点O的距离等于定长 r的点组成的图形。
O
A
B
C
隐圆
(一) 圆的有关的概念
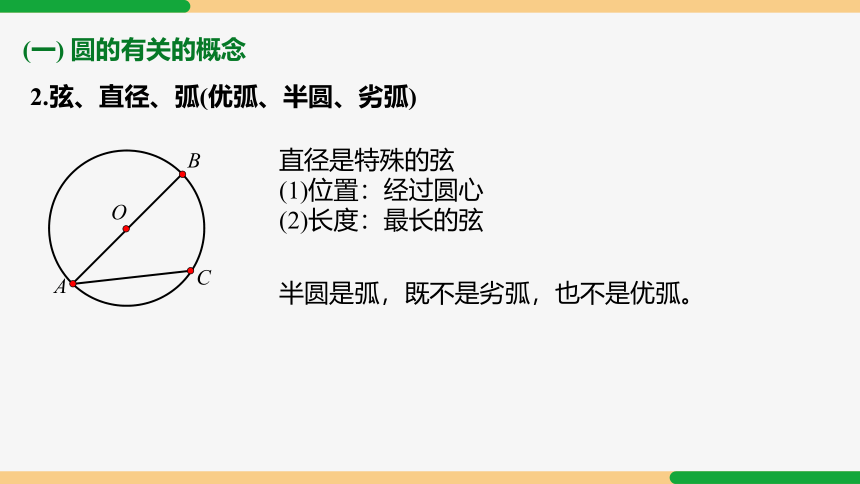
2.弦、直径、弧(优弧、半圆、劣弧)
·
C
O
A
B
直径是特殊的弦
(1)位置:经过圆心
(2)长度:最长的弦
半圆是弧,既不是劣弧,也不是优弧。
(一) 圆的有关的概念
3.同心圆、等圆、等弧
B
A
O
能够互相重合的两个圆叫做等圆。
注意:1.半径相等的两个圆是等圆;
2.同圆或等圆的半径相等。
在同圆或等圆中,能够互相重合的弧叫做等弧。
(二) 垂径定理
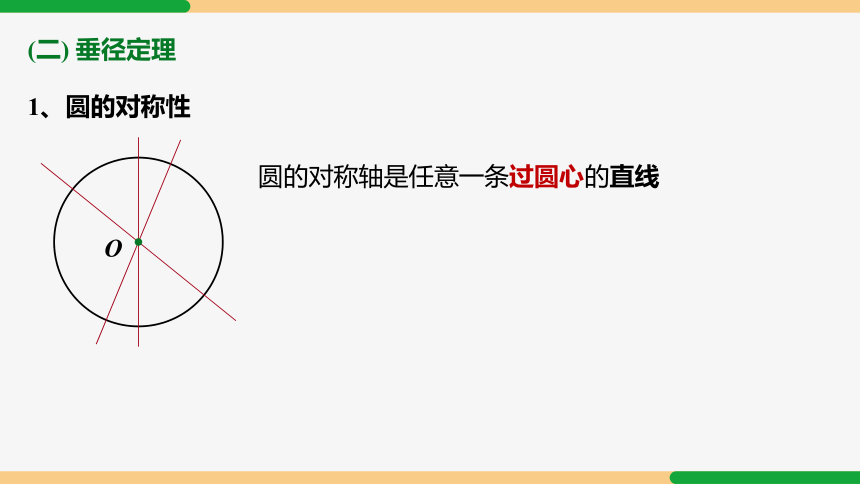
1、圆的对称性
O
圆的对称轴是任意一条过圆心的直线
(二) 垂径定理
2、垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
·
O
A
A′
C
D
M
∵ CD 是⊙O 的直径,CD⊥AA′,(条件)
∴AM = A′M,
(结论)
(二) 垂径定理
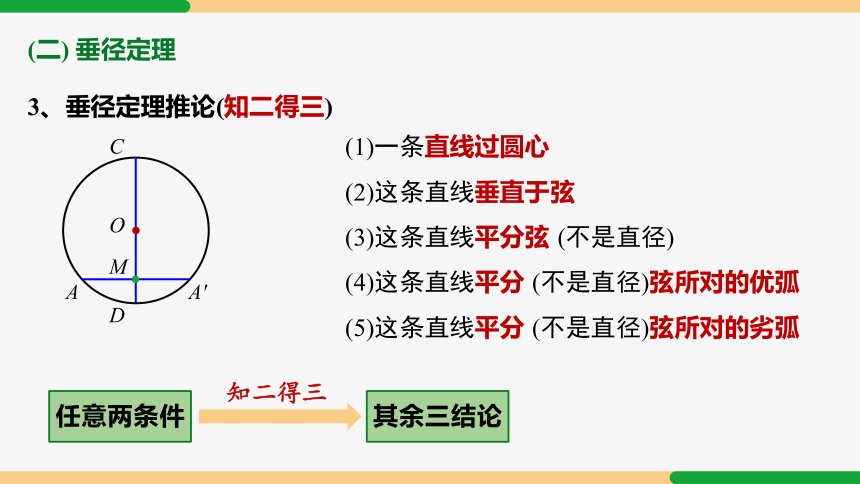
3、垂径定理推论(知二得三)
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦 (不是直径)
(4)这条直线平分 (不是直径)弦所对的优弧
(5)这条直线平分 (不是直径)弦所对的劣弧
任意两条件
其余三结论
知二得三
·
O
A
A′
C
D
M
(二) 垂径定理
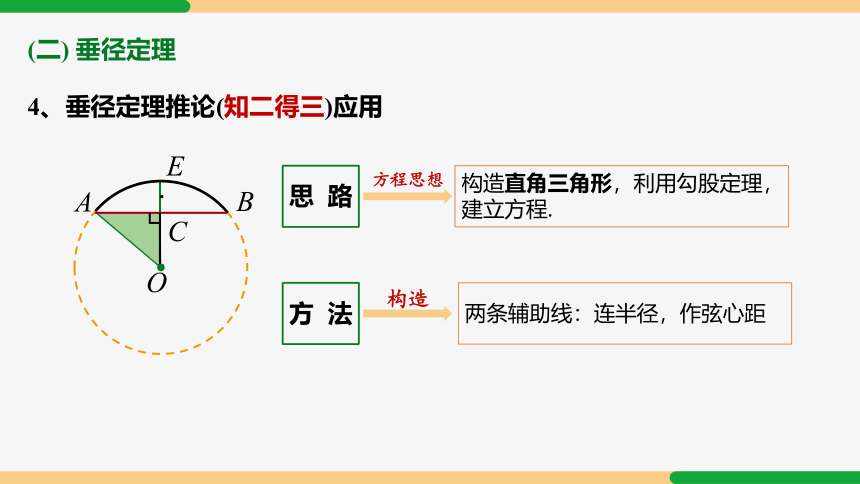
4、垂径定理推论(知二得三)应用
·
·
O
A
B
E
C
构造直角三角形,利用勾股定理,建立方程.
思路
方程思想
方法
两条辅助线:连半径,作弦心距
构造
(三) 圆心、弧、弦之间的关系
1、旋转不变性
圆是中心对称图形,圆心就是它的对称中心
O
圆绕圆心旋转任意角度,所得的图形与原图形重合
(三) 圆心、弧、弦之间的关系
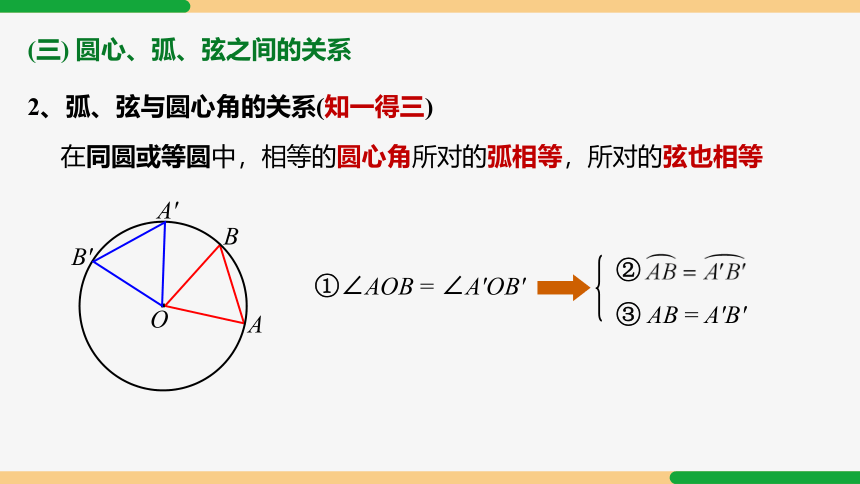
2、弧、弦与圆心角的关系(知一得三)
A′
·
O
A
B
B′
①∠AOB = ∠A′OB′
③ AB = A′B′
②
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等
(三) 圆心、弧、弦之间的关系
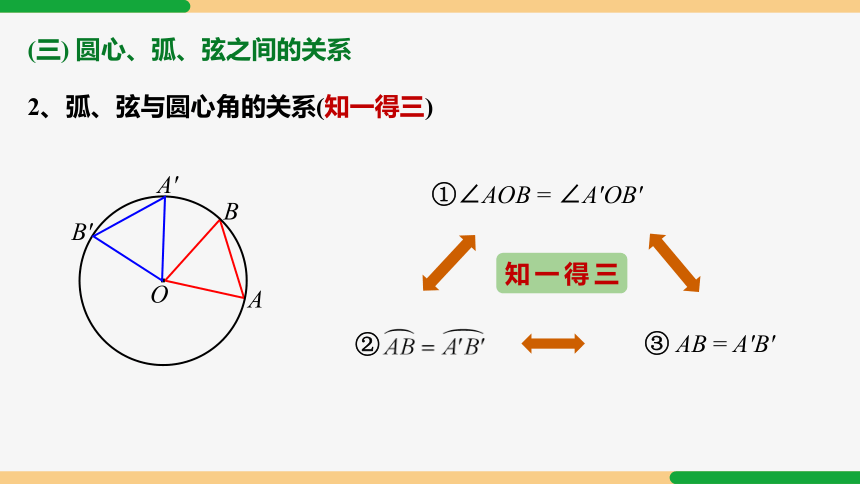
2、弧、弦与圆心角的关系(知一得三)
A′
·
O
A
B
B′
①∠AOB = ∠A′OB′
③ AB = A′B′
②
知一得三
(四) 圆周角定理
1、圆周角与圆心角
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
A
B
O
C
圆心 O 在∠BAC 的内部
圆心 O 在
∠BAC 的一边上
圆心 O 在
∠BAC 的外部
(四) 圆周角定理
2、圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
(四) 圆周角定理
3、圆周角定理推论1
同弧或等弧所对的圆周角相等
A
B
O
C
D
C
A
B
O
D
角相等在同弧或等弧上(隐圆)
隐圆
(四) 圆周角定理
4、圆周角定理推论2
半圆(或直径)所对的圆周角是直角,
90° 的圆周角所对的弦是直径
A
B
O
C
隐圆
O
(四) 圆周角定理
5、圆的内接四边形
圆的内接四边形的对角互补
二、与圆有关的位置关系
(一) 点和圆的位置关系
1.点和圆的位置关系
设⊙O 的半径为r,点P到圆心的距离OP = d,则有:
d <r
d = r
d >r
点P 在⊙O 内
点P 在⊙O 上
点P 在⊙O 外
·
r
C
O
A
B
(一) 点和圆的位置关系
2.过点作圆
D
E
G
F
●
O
A
B
C
(一) 点和圆的位置关系
3.三角形的外接圆
三角形的外接圆:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
三角形的外心:外接圆的圆心是三角形三条边的垂直平分线的交点,叫做三角形的外心.
外心:到三角形的三个顶点的距离相等。
(一) 点和圆的位置关系
4.反证法
反证法步骤
假设原命题不成立
推理证明
得出矛盾
原命题成立
图形
直线与圆的位置
公共点个数
距离 d 与半径 r
二、与圆有关的位置关系
(二) 直线和圆的位置关系
1.直线和圆的位置关系
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
(二) 直线和圆的位置关系
2.切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
A
B
C
O
∵ OA 为⊙O 的半径,
BC⊥OA 于A,
∴BC 为⊙O 的切线.
常见证切线作辅助线的方法
有交点:连半径,证垂直;
无交点:作垂直,证相等(证明 d = r ).
(二) 直线和圆的位置关系
3.切线的性质
圆的切线垂直于过切点的半径.
A
B
C
O
∵ BC 为⊙O 的切
∴线.BC⊥OA 于A,
辅助线:有切点、连半径,得垂直
(二) 直线和圆的位置关系
4.切线长定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
∵ PA、PB 分别切☉O 于 A、B,
∴ PA = PB,
∠OPA = ∠OPB.
切线长定理的变形
如图 PA 与 PB 是☉O 的两条切线,A、B 为切点,
则 PA = PB, ∠OPA = ∠OPB.
(二) 直线和圆的位置关系
5.内切圆相关定义
1. 与三角形三边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做这个三角形的内心.
3. 这个三角形叫做这个圆的外切三角形.
内心 三个内角的平分线的交点
圆心到三边距离相等
A
B
C
O
D
三、正多边形和圆
1.正多边形和圆
类比
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所对的圆心角
正多边形的中心角
圆心到弦的距离
正多边形的边心距
2.圆内接正多边形的辅助线
2. 作边心距,构造直角三角形.
1. 连半径,得中心角;
四、弧长及扇形面积
(一)弧长和面积
圆的周长
C = 2πR
弧长
圆的面积
S = πR2
扇形面积
弓形面积
四、弧长及扇形面积
(二)圆柱的侧面积和全面积
展开
h
r
h
2πr
πr2
πr2
四、弧长及扇形面积
(三)圆锥的侧面积和全面积
O
C
C= = 2
n =
S扇形= = l
h
r
l
r2 + h2 = l2
知识结构与考点
第二十四章 圆
| 小结与复习 第1课时 |
知识结构
圆
垂径定证理
轴对称
中心对称
知二得三
圆心角、弧、弦
知一得三
圆周角定理
相关推论
点与圆的位置
直线与圆的位置
三角形的外接圆
切线
切线长定理
弧长
扇形面积
等分圆
圆柱的侧面积与全面积
圆锥的侧面积与全面积
展开图
基本性质
位置关系
正多边形
有关计算
一 圆的有关的性质
(一) 圆的有关的概念
1.圆的两种定义
(1)旋转:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。
O
r
A
(2)集合:定点O的距离等于定长 r的点组成的图形。
O
A
B
C
隐圆
(一) 圆的有关的概念
2.弦、直径、弧(优弧、半圆、劣弧)
·
C
O
A
B
直径是特殊的弦
(1)位置:经过圆心
(2)长度:最长的弦
半圆是弧,既不是劣弧,也不是优弧。
(一) 圆的有关的概念
3.同心圆、等圆、等弧
B
A
O
能够互相重合的两个圆叫做等圆。
注意:1.半径相等的两个圆是等圆;
2.同圆或等圆的半径相等。
在同圆或等圆中,能够互相重合的弧叫做等弧。
(二) 垂径定理
1、圆的对称性
O
圆的对称轴是任意一条过圆心的直线
(二) 垂径定理
2、垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
·
O
A
A′
C
D
M
∵ CD 是⊙O 的直径,CD⊥AA′,(条件)
∴AM = A′M,
(结论)
(二) 垂径定理
3、垂径定理推论(知二得三)
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦 (不是直径)
(4)这条直线平分 (不是直径)弦所对的优弧
(5)这条直线平分 (不是直径)弦所对的劣弧
任意两条件
其余三结论
知二得三
·
O
A
A′
C
D
M
(二) 垂径定理
4、垂径定理推论(知二得三)应用
·
·
O
A
B
E
C
构造直角三角形,利用勾股定理,建立方程.
思路
方程思想
方法
两条辅助线:连半径,作弦心距
构造
(三) 圆心、弧、弦之间的关系
1、旋转不变性
圆是中心对称图形,圆心就是它的对称中心
O
圆绕圆心旋转任意角度,所得的图形与原图形重合
(三) 圆心、弧、弦之间的关系
2、弧、弦与圆心角的关系(知一得三)
A′
·
O
A
B
B′
①∠AOB = ∠A′OB′
③ AB = A′B′
②
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等
(三) 圆心、弧、弦之间的关系
2、弧、弦与圆心角的关系(知一得三)
A′
·
O
A
B
B′
①∠AOB = ∠A′OB′
③ AB = A′B′
②
知一得三
(四) 圆周角定理
1、圆周角与圆心角
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
A
B
O
C
圆心 O 在∠BAC 的内部
圆心 O 在
∠BAC 的一边上
圆心 O 在
∠BAC 的外部
(四) 圆周角定理
2、圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
(四) 圆周角定理
3、圆周角定理推论1
同弧或等弧所对的圆周角相等
A
B
O
C
D
C
A
B
O
D
角相等在同弧或等弧上(隐圆)
隐圆
(四) 圆周角定理
4、圆周角定理推论2
半圆(或直径)所对的圆周角是直角,
90° 的圆周角所对的弦是直径
A
B
O
C
隐圆
O
(四) 圆周角定理
5、圆的内接四边形
圆的内接四边形的对角互补
二、与圆有关的位置关系
(一) 点和圆的位置关系
1.点和圆的位置关系
设⊙O 的半径为r,点P到圆心的距离OP = d,则有:
d <r
d = r
d >r
点P 在⊙O 内
点P 在⊙O 上
点P 在⊙O 外
·
r
C
O
A
B
(一) 点和圆的位置关系
2.过点作圆
D
E
G
F
●
O
A
B
C
(一) 点和圆的位置关系
3.三角形的外接圆
三角形的外接圆:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
三角形的外心:外接圆的圆心是三角形三条边的垂直平分线的交点,叫做三角形的外心.
外心:到三角形的三个顶点的距离相等。
(一) 点和圆的位置关系
4.反证法
反证法步骤
假设原命题不成立
推理证明
得出矛盾
原命题成立
图形
直线与圆的位置
公共点个数
距离 d 与半径 r
二、与圆有关的位置关系
(二) 直线和圆的位置关系
1.直线和圆的位置关系
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
(二) 直线和圆的位置关系
2.切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
A
B
C
O
∵ OA 为⊙O 的半径,
BC⊥OA 于A,
∴BC 为⊙O 的切线.
常见证切线作辅助线的方法
有交点:连半径,证垂直;
无交点:作垂直,证相等(证明 d = r ).
(二) 直线和圆的位置关系
3.切线的性质
圆的切线垂直于过切点的半径.
A
B
C
O
∵ BC 为⊙O 的切
∴线.BC⊥OA 于A,
辅助线:有切点、连半径,得垂直
(二) 直线和圆的位置关系
4.切线长定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
∵ PA、PB 分别切☉O 于 A、B,
∴ PA = PB,
∠OPA = ∠OPB.
切线长定理的变形
如图 PA 与 PB 是☉O 的两条切线,A、B 为切点,
则 PA = PB, ∠OPA = ∠OPB.
(二) 直线和圆的位置关系
5.内切圆相关定义
1. 与三角形三边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做这个三角形的内心.
3. 这个三角形叫做这个圆的外切三角形.
内心 三个内角的平分线的交点
圆心到三边距离相等
A
B
C
O
D
三、正多边形和圆
1.正多边形和圆
类比
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所对的圆心角
正多边形的中心角
圆心到弦的距离
正多边形的边心距
2.圆内接正多边形的辅助线
2. 作边心距,构造直角三角形.
1. 连半径,得中心角;
四、弧长及扇形面积
(一)弧长和面积
圆的周长
C = 2πR
弧长
圆的面积
S = πR2
扇形面积
弓形面积
四、弧长及扇形面积
(二)圆柱的侧面积和全面积
展开
h
r
h
2πr
πr2
πr2
四、弧长及扇形面积
(三)圆锥的侧面积和全面积
O
C
C= = 2
n =
S扇形= = l
h
r
l
r2 + h2 = l2
同课章节目录
