24.2.2 第2课时 切线的判定 课件(共16张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 24.2.2 第2课时 切线的判定 课件(共16张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 716.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 05:18:46 | ||
图片预览




文档简介
(共16张PPT)
切线的判定
24.2 点和圆、直线和圆的位置关系
| 24.2.2 直线和圆的位置关系 第2课时 |
课堂导航
理解和掌握切线的判定定理。
利用切线的判定定理进行计算
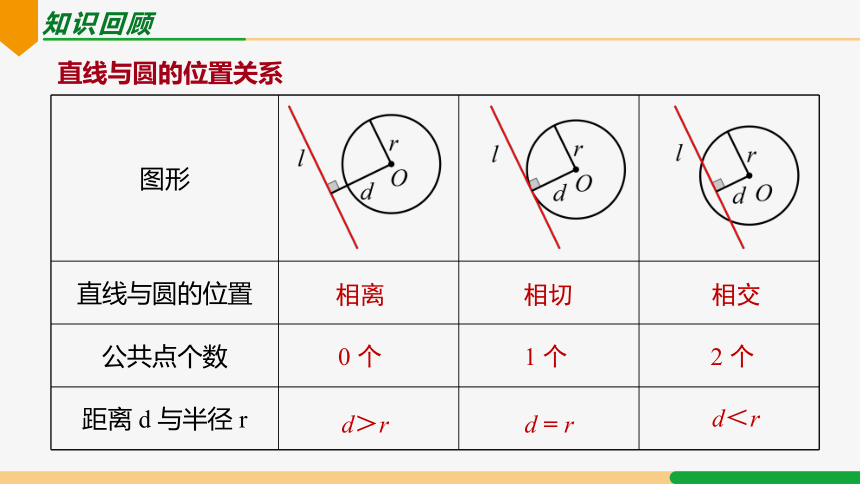
知识回顾
图形
直线与圆的位置
公共点个数
距离 d 与半径 r
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
直线与圆的位置关系
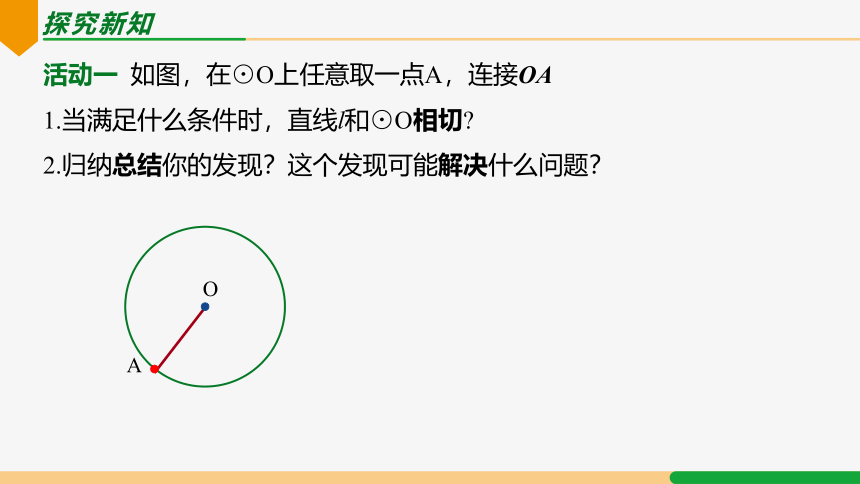
探究新知
活动一 如图,在⊙O上任意取一点A,连接OA
1.当满足什么条件时,直线l和⊙O相切
2.归纳总结你的发现?这个发现可能解决什么问题?
O
A
知识要点1
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
A
B
C
O
∵ OA 为⊙O 的半径,
BC⊥OA 于A,
∴BC 为⊙O 的切线.
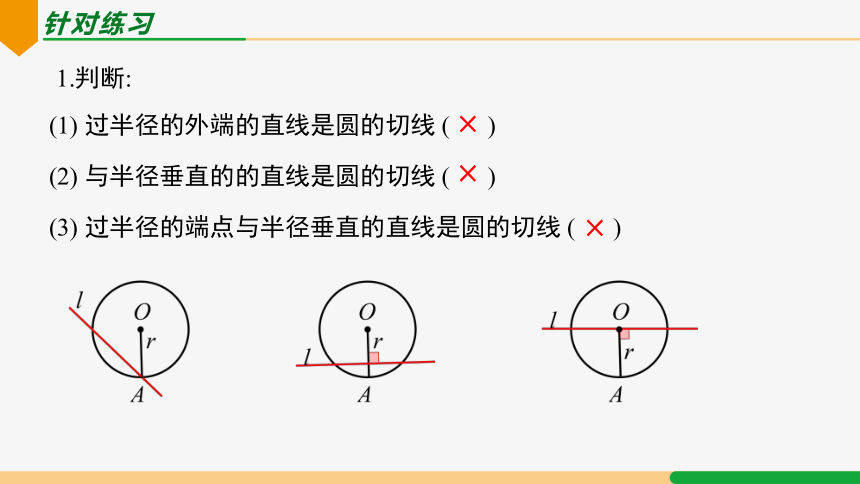
针对练习
1.判断:
(1) 过半径的外端的直线是圆的切线 ( )
(2) 与半径垂直的的直线是圆的切线 ( )
(3) 过半径的端点与半径垂直的直线是圆的切线 ( )
×
×
×
典例讲解
例1 如图,已知:直线 AB 经过⊙O 上的点 C 并且OA = OB,CA = CB.
求证:直线 AB 是⊙O 的切线.
证明:连接 OC (如图).
∵ OA = OB,CA = CB,
∴ AB ⊥ OC.
∴ OC 是⊙O 的半径.
∴ AB 是⊙O 的切线.
E
例2 如图,在 Rt△ABC 中,∠ABC = 90°,∠BAC 的平分线交 BC 于 D,以 D 为圆心,DB 长为半径作⊙D.
求证:AC 是⊙O 的切线.
证明:如图,过 D 作 DE⊥AC 于 E.
∵∠ABC = 90°,∴ DB⊥AB.
又∵ AD 平分∠BAC,DE⊥AC,
∴ DE = DB.
∴ AC 是⊙O 的切线.
知识要点1
常见证切线作辅助线的方法
有交点
连半径,证垂直;
E
无交点
作垂直,证相等(证明 d = r ).
例3 如图,以线段 AB 为直径作 ⊙O ,交射线 AC于点 C, AD 平分∠CAB 交 ⊙O 于点 D 作直线 DE⊥AC 于点 E,交 AB 的延长线于点 F.连接 BD 并延长交 AC 于点 M. 求证:直线 DE 是⊙O 的切线.
证明:连接 OD.
∵AD 平分∠CAB,OA = OD,
∴∠ODA =∠OAD =∠DAC.
∴ OD∥AC.
又∵ DE⊥AC ,
∴∠ODF =∠AED = 90°,
即直线 DE 是⊙O 的切线.
知识小结
定理法
切线的判定
判定方法
数量法
交点法
辅助线
有交点:连半径,证垂直
无交点:作垂直,证相等
A
B
C
O
课堂练习
1 判断下列命题是否正确
⑴ 经过半径外端的直线是圆的切线. ( )
⑵ 垂直于半径的直线是圆的切线. ( )
⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
⑷ 和圆只有一个公共点的直线是圆的切线. ( )
⑸ 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
如图,A 是☉O 上一点,且 AO = 5,PO = 13, AP = 12,则 PA 与☉O 的位置关系是 .
相切
已知OA=OB=5,AB=8,⊙O的直径为6.求证:直线AB是⊙O的切线.
证明:过点O作OC⊥AB于C,
∵OA=OB=5,AB=8,
∴AC=BC=4.
在Rt△AOC中,根据勾股定理可得:OC=3
∵⊙O的直径为6
∴OC是⊙O的半径
∴直线AB是⊙O的切线.
C
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB延长线相交于点P.若∠COB=2∠PCB,求证:PC是⊙O的切线.
证明:连接AC,
∵OA=OC,∴∠A=∠ACO.
∴∠COB=2∠ACO.
又∵∠COB=2∠PCB,∴∠ACO=∠PCB.
∵AB是⊙O的直径,∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,即OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线.
切线的判定
24.2 点和圆、直线和圆的位置关系
| 24.2.2 直线和圆的位置关系 第2课时 |
课堂导航
理解和掌握切线的判定定理。
利用切线的判定定理进行计算
知识回顾
图形
直线与圆的位置
公共点个数
距离 d 与半径 r
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
直线与圆的位置关系
探究新知
活动一 如图,在⊙O上任意取一点A,连接OA
1.当满足什么条件时,直线l和⊙O相切
2.归纳总结你的发现?这个发现可能解决什么问题?
O
A
知识要点1
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
A
B
C
O
∵ OA 为⊙O 的半径,
BC⊥OA 于A,
∴BC 为⊙O 的切线.
针对练习
1.判断:
(1) 过半径的外端的直线是圆的切线 ( )
(2) 与半径垂直的的直线是圆的切线 ( )
(3) 过半径的端点与半径垂直的直线是圆的切线 ( )
×
×
×
典例讲解
例1 如图,已知:直线 AB 经过⊙O 上的点 C 并且OA = OB,CA = CB.
求证:直线 AB 是⊙O 的切线.
证明:连接 OC (如图).
∵ OA = OB,CA = CB,
∴ AB ⊥ OC.
∴ OC 是⊙O 的半径.
∴ AB 是⊙O 的切线.
E
例2 如图,在 Rt△ABC 中,∠ABC = 90°,∠BAC 的平分线交 BC 于 D,以 D 为圆心,DB 长为半径作⊙D.
求证:AC 是⊙O 的切线.
证明:如图,过 D 作 DE⊥AC 于 E.
∵∠ABC = 90°,∴ DB⊥AB.
又∵ AD 平分∠BAC,DE⊥AC,
∴ DE = DB.
∴ AC 是⊙O 的切线.
知识要点1
常见证切线作辅助线的方法
有交点
连半径,证垂直;
E
无交点
作垂直,证相等(证明 d = r ).
例3 如图,以线段 AB 为直径作 ⊙O ,交射线 AC于点 C, AD 平分∠CAB 交 ⊙O 于点 D 作直线 DE⊥AC 于点 E,交 AB 的延长线于点 F.连接 BD 并延长交 AC 于点 M. 求证:直线 DE 是⊙O 的切线.
证明:连接 OD.
∵AD 平分∠CAB,OA = OD,
∴∠ODA =∠OAD =∠DAC.
∴ OD∥AC.
又∵ DE⊥AC ,
∴∠ODF =∠AED = 90°,
即直线 DE 是⊙O 的切线.
知识小结
定理法
切线的判定
判定方法
数量法
交点法
辅助线
有交点:连半径,证垂直
无交点:作垂直,证相等
A
B
C
O
课堂练习
1 判断下列命题是否正确
⑴ 经过半径外端的直线是圆的切线. ( )
⑵ 垂直于半径的直线是圆的切线. ( )
⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
⑷ 和圆只有一个公共点的直线是圆的切线. ( )
⑸ 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
如图,A 是☉O 上一点,且 AO = 5,PO = 13, AP = 12,则 PA 与☉O 的位置关系是 .
相切
已知OA=OB=5,AB=8,⊙O的直径为6.求证:直线AB是⊙O的切线.
证明:过点O作OC⊥AB于C,
∵OA=OB=5,AB=8,
∴AC=BC=4.
在Rt△AOC中,根据勾股定理可得:OC=3
∵⊙O的直径为6
∴OC是⊙O的半径
∴直线AB是⊙O的切线.
C
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB延长线相交于点P.若∠COB=2∠PCB,求证:PC是⊙O的切线.
证明:连接AC,
∵OA=OC,∴∠A=∠ACO.
∴∠COB=2∠ACO.
又∵∠COB=2∠PCB,∴∠ACO=∠PCB.
∵AB是⊙O的直径,∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,即OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线.
同课章节目录
