14.1.1 同底数幂的乘法 课件(共16张PPT)-2023-2024学年八年级数学上册同步课件 练习(人教版)
文档属性
| 名称 | 14.1.1 同底数幂的乘法 课件(共16张PPT)-2023-2024学年八年级数学上册同步课件 练习(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 588.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第14.1.1同底数幂的乘法
人教版数学八年级上册
1.理解同底数幂的乘法的性质,会利用这一性质进行同底数幂的乘法运算.
2.掌握同底数幂的乘法的运算性质的推导.
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
学习目标
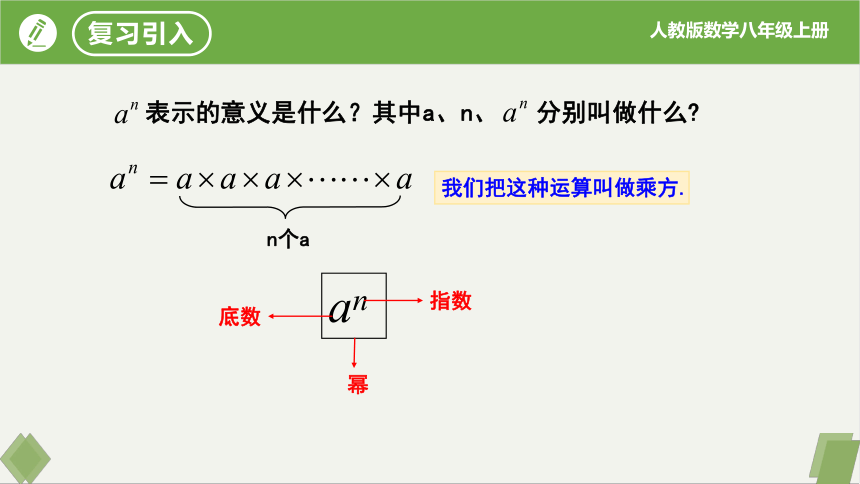
表示的意义是什么?其中a、n、 分别叫做什么
n个a
an
底数
指数
幂
我们把这种运算叫做乘方.
复习引入
在2010年全球超级计算机排行榜中,中国首台千万亿次超级计算机系统“天河一号”雄居第一,其实测运算速度可以达到每秒2570万亿次.
问题1 一种电子计算机每秒可进行1千万亿( )次运算,它工作 s可进行多少次运算?
15个10
18个10
3个10
互动新授
根据乘方的意义填空,观察计算结果,你能发现什么规律?
7
5
m+n
(m,n是正整数)
思考:观察上面各题左右两边,底数、指数有什么关系?
相乘结果的底数与原来底数相同,指数是原来两个幂的指数的和.
互动新授
等于什么?(a是任意底数,m、n都是正整数)
m个a
n个a
m+n个a
你能用一句语言来叙述这一规律吗?
互动新授
同底数幂相乘,底数不变,指数相加.
(m、n都是正整数)
方法归纳:同底数幂的乘法注意应两点:一是必须是同底数幂的乘法才能运用这个法则;二是运用这个法则计算时一定是底数不变,指数相加,即 (m、n都是正整数)
互动新授
例1 计算:
(1) x2·x5; (2) a·a6;
(3) (-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解: (1)x2·x5 =x2+5 =x7.
(4)xm·x3m+1=xm+3m+1 = x4m+1.
(3)(-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8=256.
(2)a·a6 =a1+6 =a7.
典例精析
1.计算:
(1)b5·b ; (2) 10×102×103;
(3)–a2·a6; (4) y2n·yn+1.
解:(1)b5·b =x5+1 =b6.
(2)10×102×103=101+2+3 =106.
(3)-a2·a6=-a2+6=-a8.
(4)y2n·yn+1=y2n+n+1=y3n+1
小试牛刀
1.下列运算中正确的是( )
A.x2 x2=2x2 B.x2 x3=x6
C.x2 x3=x5 D.(-x)2 (-x)3=(-x)6=x6
C
解:A.x2 x2=x2+2=x4
B.C.x2 x3=x2+3=x5
D.(-x)2 (-x)3=(-x)2+3=(-x)5=-x5
课堂检测
4.填空:
(1)x5 ·( )=x 8 (2)a·( )=a6
(3)x·x3( )= x7 (4)xm ·( )=x3m
x3
a5
x3
x2m
2.计算a2 a3的结果是( )
A.a6 B.a5 C.2a3 D.a
3.计算2x3·x2的结果是( )
A.2x B.2x5 C.2x6 D.x5
B
B
课堂检测
1.已知xa=2,xb=3,求xa+b.
2.已知x3·xa·x2a+1=x31,求a的值.
解:xa+b=xa·xb=2×3=6
解:x3·xa·x2a+1=x3+a+2a+1=x3a+4=x31
∴3a+4=31,则a=9
拓展训练
3.计算:
①(a+b)2×(a+b)4×[-(a+b)]7
②(m-n)3×(m-n)4×(n-m)7
解:原式=(a+b)2×(a+b)4×[-(a+b)7 ]
= - (a+b)13
解:原式=(m-n)3×(m-n)4× [-(m-n)7 ]
= -(m-n)14
当底数为一个多项式的时候,我们可以把这个多项式看成一个整体.
拓展训练
同底数幂
的乘法
法则:同底数幂相乘,底数
不变,指数相加.
am×an=am+n (m,n为正整数)
课堂小结
(3) -x2 (-x)8 = -x2 x8= -x10 .
(2) (-10)3×(-10)5 =(-10)3+5=(-10)8=108 ;
1.计算:
(1) x7 x ; (2) (-10)3×(-10)5 ;
(3) -x2 (-x)8 ; (4)(x+3y)3 (x+3y)2 (x+3y) ;
(5) (x-y)3 (y-x)4 .
解:(1) x7 x=x7+1=x8 ;
(4) (x+3y)3 (x+3y)2 (x+3y)=(x+3y)3+2+1=(x+3y)6 ;
(5) (x-y)3 (y-x)4=(x-y)3 (x-y)4=(x-y)7 .
课后作业
谢谢聆听
第14.1.1同底数幂的乘法
人教版数学八年级上册
1.理解同底数幂的乘法的性质,会利用这一性质进行同底数幂的乘法运算.
2.掌握同底数幂的乘法的运算性质的推导.
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
学习目标
表示的意义是什么?其中a、n、 分别叫做什么
n个a
an
底数
指数
幂
我们把这种运算叫做乘方.
复习引入
在2010年全球超级计算机排行榜中,中国首台千万亿次超级计算机系统“天河一号”雄居第一,其实测运算速度可以达到每秒2570万亿次.
问题1 一种电子计算机每秒可进行1千万亿( )次运算,它工作 s可进行多少次运算?
15个10
18个10
3个10
互动新授
根据乘方的意义填空,观察计算结果,你能发现什么规律?
7
5
m+n
(m,n是正整数)
思考:观察上面各题左右两边,底数、指数有什么关系?
相乘结果的底数与原来底数相同,指数是原来两个幂的指数的和.
互动新授
等于什么?(a是任意底数,m、n都是正整数)
m个a
n个a
m+n个a
你能用一句语言来叙述这一规律吗?
互动新授
同底数幂相乘,底数不变,指数相加.
(m、n都是正整数)
方法归纳:同底数幂的乘法注意应两点:一是必须是同底数幂的乘法才能运用这个法则;二是运用这个法则计算时一定是底数不变,指数相加,即 (m、n都是正整数)
互动新授
例1 计算:
(1) x2·x5; (2) a·a6;
(3) (-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解: (1)x2·x5 =x2+5 =x7.
(4)xm·x3m+1=xm+3m+1 = x4m+1.
(3)(-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8=256.
(2)a·a6 =a1+6 =a7.
典例精析
1.计算:
(1)b5·b ; (2) 10×102×103;
(3)–a2·a6; (4) y2n·yn+1.
解:(1)b5·b =x5+1 =b6.
(2)10×102×103=101+2+3 =106.
(3)-a2·a6=-a2+6=-a8.
(4)y2n·yn+1=y2n+n+1=y3n+1
小试牛刀
1.下列运算中正确的是( )
A.x2 x2=2x2 B.x2 x3=x6
C.x2 x3=x5 D.(-x)2 (-x)3=(-x)6=x6
C
解:A.x2 x2=x2+2=x4
B.C.x2 x3=x2+3=x5
D.(-x)2 (-x)3=(-x)2+3=(-x)5=-x5
课堂检测
4.填空:
(1)x5 ·( )=x 8 (2)a·( )=a6
(3)x·x3( )= x7 (4)xm ·( )=x3m
x3
a5
x3
x2m
2.计算a2 a3的结果是( )
A.a6 B.a5 C.2a3 D.a
3.计算2x3·x2的结果是( )
A.2x B.2x5 C.2x6 D.x5
B
B
课堂检测
1.已知xa=2,xb=3,求xa+b.
2.已知x3·xa·x2a+1=x31,求a的值.
解:xa+b=xa·xb=2×3=6
解:x3·xa·x2a+1=x3+a+2a+1=x3a+4=x31
∴3a+4=31,则a=9
拓展训练
3.计算:
①(a+b)2×(a+b)4×[-(a+b)]7
②(m-n)3×(m-n)4×(n-m)7
解:原式=(a+b)2×(a+b)4×[-(a+b)7 ]
= - (a+b)13
解:原式=(m-n)3×(m-n)4× [-(m-n)7 ]
= -(m-n)14
当底数为一个多项式的时候,我们可以把这个多项式看成一个整体.
拓展训练
同底数幂
的乘法
法则:同底数幂相乘,底数
不变,指数相加.
am×an=am+n (m,n为正整数)
课堂小结
(3) -x2 (-x)8 = -x2 x8= -x10 .
(2) (-10)3×(-10)5 =(-10)3+5=(-10)8=108 ;
1.计算:
(1) x7 x ; (2) (-10)3×(-10)5 ;
(3) -x2 (-x)8 ; (4)(x+3y)3 (x+3y)2 (x+3y) ;
(5) (x-y)3 (y-x)4 .
解:(1) x7 x=x7+1=x8 ;
(4) (x+3y)3 (x+3y)2 (x+3y)=(x+3y)3+2+1=(x+3y)6 ;
(5) (x-y)3 (y-x)4=(x-y)3 (x-y)4=(x-y)7 .
课后作业
谢谢聆听
