24.2.2 第5课时 三角形的内切圆 课件(共17张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 24.2.2 第5课时 三角形的内切圆 课件(共17张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 783.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 05:39:04 | ||
图片预览



文档简介
三角形的内切圆
24.2 点和圆、直线和圆的位置关系
| 24.2.2 直线和圆的位置关系 第5课时 |
课堂导航
掌握用尺规作三角形内切圆的方法。
三角形内切圆的相关计算
知识回顾
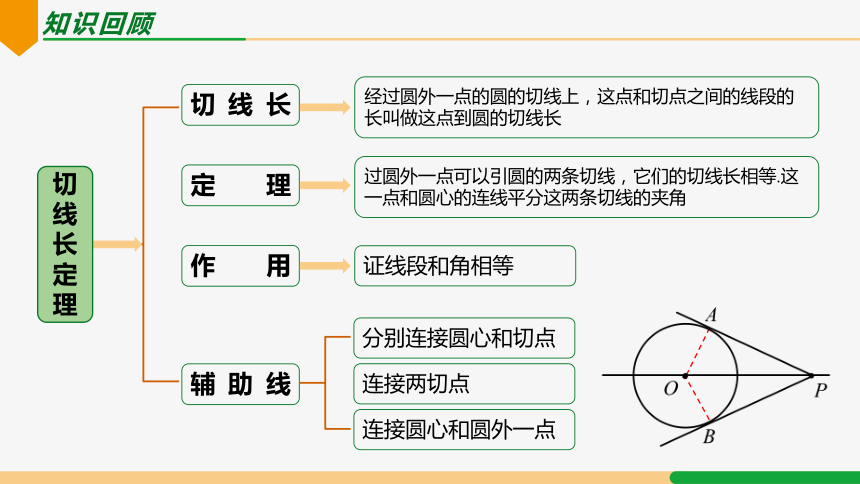
切线长定理
切线长
辅助线
分别连接圆心和切点
连接圆心和圆外一点
定理
作用
连接两切点
经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
证线段和角相等
探究新知
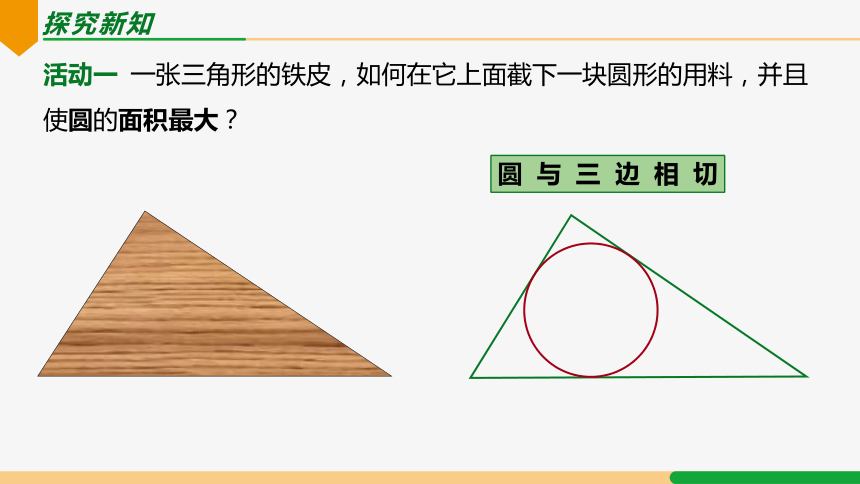
活动一 一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积最大?
圆与三边相切
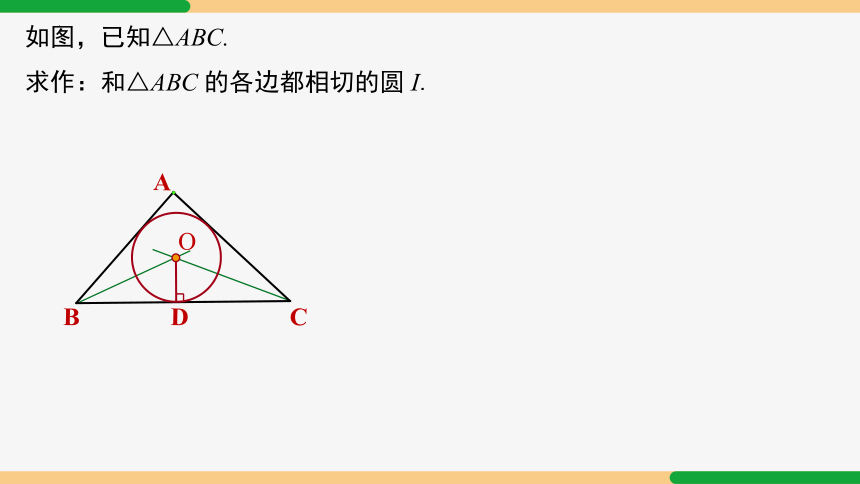
如图,已知△ABC.
求作:和△ABC 的各边都相切的圆 I.
A
B
C
O
D
知识要点1
内切圆相关定义
1. 与三角形三边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做这个三角形的内心.
3. 这个三角形叫做这个圆的外切三角形.
A
B
C
O
D
内心 三个内角的平分线的交点
圆心到三边距离相等
{8799B23B-EC83-4686-B30A-512413B5E67A}名称
图形
确定方法
性质
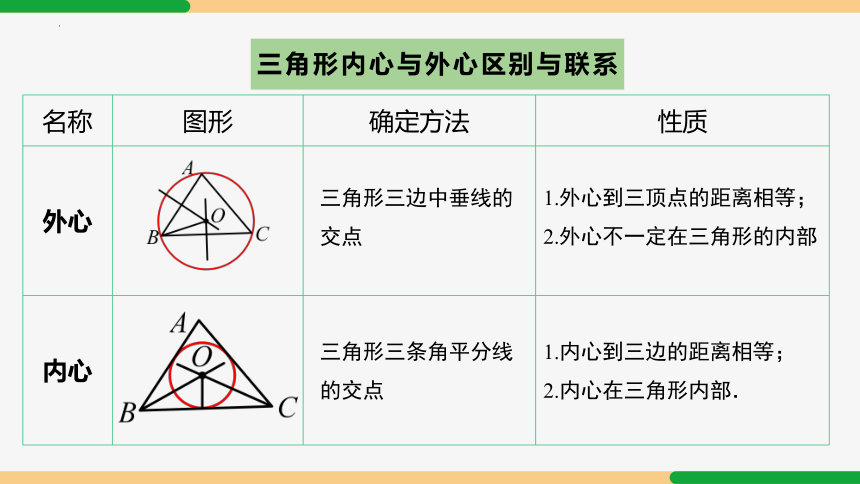
外心
内心
三角形三边中垂线的交点
1.外心到三顶点的距离相等;2.外心不一定在三角形的内部
三角形三条角平分线的交点
1.内心到三边的距离相等;
2.内心在三角形内部.
三角形内心与外心区别与联系
典例讲解
例1 如图,△ABC 的内切圆 ☉O 与 BC、CA、AB 分别相切于点 D,E,F,且 AB = 9,BC = 14,CA = 13,求 AF、BD、CE 的长.
解:
设 AF = x ,则 AE = x .
∴ CE = CD = AC - AE = 9 - x,
BF = BD = AB - AF = 13 - x.
由 BD + CD = BC,可得
(13 - x) + (9 - x) = 14,
∴ AF = 4 ,BD = 9 ,CE = 5 .
解得 x = 4.
例2 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AE、BD、CE的长。
A
F
O
E
B
D
C
方法一 设AF长为x
则BC=BD+DC
(9-x) + (13-x)=14
解得,x=4
则AE=4,BD=5,CE=9
方法二 设AF长为x,BD长为y,EC长为z
x+z =13
y+z =14
x+y = 9
解得x=4,y=5,z=9
则AE=4,BD=5,CE=9
A
F
O
E
B
D
C
例3 求边长为6 cm的等边三角形的内切圆半径与外接圆半径.
知识小结
切线长定理
辅助线
分别连接圆心和切点
连接圆心和圆外一点
定理
连接两切点
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
三角形的内接圆
内接圆
内心
半径
三个内角的平分线的交点
圆心到三边距离相等
课堂练习
(3)若∠BIC=100 °,则∠A = 度.
(2)若∠A=80 °,则∠BIC = 度.
130
20
如图,在△ABC中,点I是内心,
(1)若∠ABC=50°, ∠ACB=70°,∠BIC=_____.
A
B
C
I
(4)试探索: ∠A与∠BIC之间存在怎样的数量关系?
120°
设边长为 a 的等边三角形的高、内切圆的半径、外接圆的半径分别为 h、r、R,则下列结论不正确的是 ( )
A. h = R + r B.R = 2r
C. r =?34???? D.R = 33????
?
C
如图,☉O 为△ABC 的内切圆,AC = 10,AB = 8,BC = 9,点 D,E 分别为 BC,AC 上的点,且 DE 为☉O 的切线,则△CDE 的周长为______.
11
如图,⊙O是△ABC的内切圆,切点分别为D,E,F,∠B=60°,∠C=70°,求∠EDF的度数.
A
B
C
O
D
E
F
解: 连接OE,OF,在△ABC中,
∠A=180°- (∠B+∠C)=180°- (60°+70°)=50°
∵⊙O是△ABC的内切圆,∴AB⊥OF,AC⊥OE.
在四边形AFOE中,
∠EOF=360°-(∠A+∠AFO+∠AEO)
=360°-(50°+90°+90°)
=130°
∴∠EDF= 12∠EOF=65°
?
如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
24.2 点和圆、直线和圆的位置关系
| 24.2.2 直线和圆的位置关系 第5课时 |
课堂导航
掌握用尺规作三角形内切圆的方法。
三角形内切圆的相关计算
知识回顾
切线长定理
切线长
辅助线
分别连接圆心和切点
连接圆心和圆外一点
定理
作用
连接两切点
经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
证线段和角相等
探究新知
活动一 一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积最大?
圆与三边相切
如图,已知△ABC.
求作:和△ABC 的各边都相切的圆 I.
A
B
C
O
D
知识要点1
内切圆相关定义
1. 与三角形三边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做这个三角形的内心.
3. 这个三角形叫做这个圆的外切三角形.
A
B
C
O
D
内心 三个内角的平分线的交点
圆心到三边距离相等
{8799B23B-EC83-4686-B30A-512413B5E67A}名称
图形
确定方法
性质
外心
内心
三角形三边中垂线的交点
1.外心到三顶点的距离相等;2.外心不一定在三角形的内部
三角形三条角平分线的交点
1.内心到三边的距离相等;
2.内心在三角形内部.
三角形内心与外心区别与联系
典例讲解
例1 如图,△ABC 的内切圆 ☉O 与 BC、CA、AB 分别相切于点 D,E,F,且 AB = 9,BC = 14,CA = 13,求 AF、BD、CE 的长.
解:
设 AF = x ,则 AE = x .
∴ CE = CD = AC - AE = 9 - x,
BF = BD = AB - AF = 13 - x.
由 BD + CD = BC,可得
(13 - x) + (9 - x) = 14,
∴ AF = 4 ,BD = 9 ,CE = 5 .
解得 x = 4.
例2 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AE、BD、CE的长。
A
F
O
E
B
D
C
方法一 设AF长为x
则BC=BD+DC
(9-x) + (13-x)=14
解得,x=4
则AE=4,BD=5,CE=9
方法二 设AF长为x,BD长为y,EC长为z
x+z =13
y+z =14
x+y = 9
解得x=4,y=5,z=9
则AE=4,BD=5,CE=9
A
F
O
E
B
D
C
例3 求边长为6 cm的等边三角形的内切圆半径与外接圆半径.
知识小结
切线长定理
辅助线
分别连接圆心和切点
连接圆心和圆外一点
定理
连接两切点
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
三角形的内接圆
内接圆
内心
半径
三个内角的平分线的交点
圆心到三边距离相等
课堂练习
(3)若∠BIC=100 °,则∠A = 度.
(2)若∠A=80 °,则∠BIC = 度.
130
20
如图,在△ABC中,点I是内心,
(1)若∠ABC=50°, ∠ACB=70°,∠BIC=_____.
A
B
C
I
(4)试探索: ∠A与∠BIC之间存在怎样的数量关系?
120°
设边长为 a 的等边三角形的高、内切圆的半径、外接圆的半径分别为 h、r、R,则下列结论不正确的是 ( )
A. h = R + r B.R = 2r
C. r =?34???? D.R = 33????
?
C
如图,☉O 为△ABC 的内切圆,AC = 10,AB = 8,BC = 9,点 D,E 分别为 BC,AC 上的点,且 DE 为☉O 的切线,则△CDE 的周长为______.
11
如图,⊙O是△ABC的内切圆,切点分别为D,E,F,∠B=60°,∠C=70°,求∠EDF的度数.
A
B
C
O
D
E
F
解: 连接OE,OF,在△ABC中,
∠A=180°- (∠B+∠C)=180°- (60°+70°)=50°
∵⊙O是△ABC的内切圆,∴AB⊥OF,AC⊥OE.
在四边形AFOE中,
∠EOF=360°-(∠A+∠AFO+∠AEO)
=360°-(50°+90°+90°)
=130°
∴∠EDF= 12∠EOF=65°
?
如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
同课章节目录
