24.3 第2课时 画圆内接正多边形 课件(共12张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 24.3 第2课时 画圆内接正多边形 课件(共12张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 25.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 05:37:29 | ||
图片预览



文档简介
(共12张PPT)
画圆内接正多边形
24.3 正多边形和圆
| 24.3 正多边形和圆 第2课时 |
课堂导航
画圆内接正多边形
情景引入
观察:下图的这些由正边形组成的图案,怎样画正多边形。
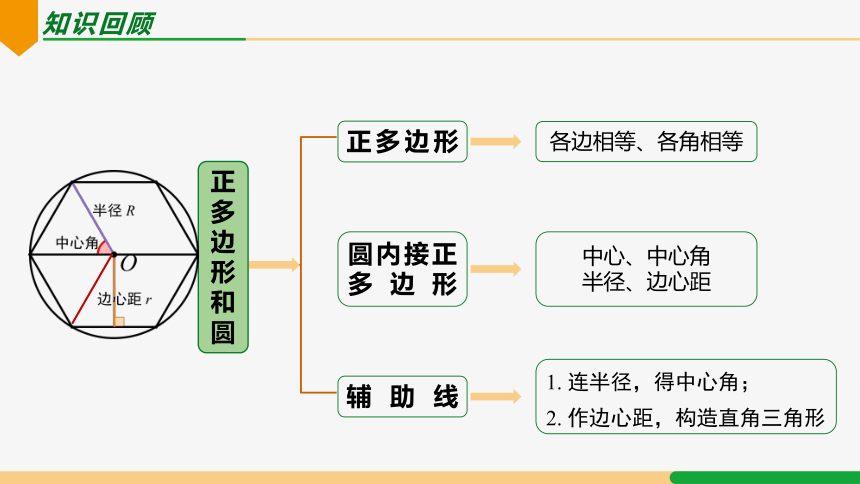
知识回顾
各边相等、各角相等
定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
正多边形
正多边形和圆
圆内接正多边形
辅助线
中心、中心角
半径、边心距
1. 连半径,得中心角;
2. 作边心距,构造直角三角形
探究新知
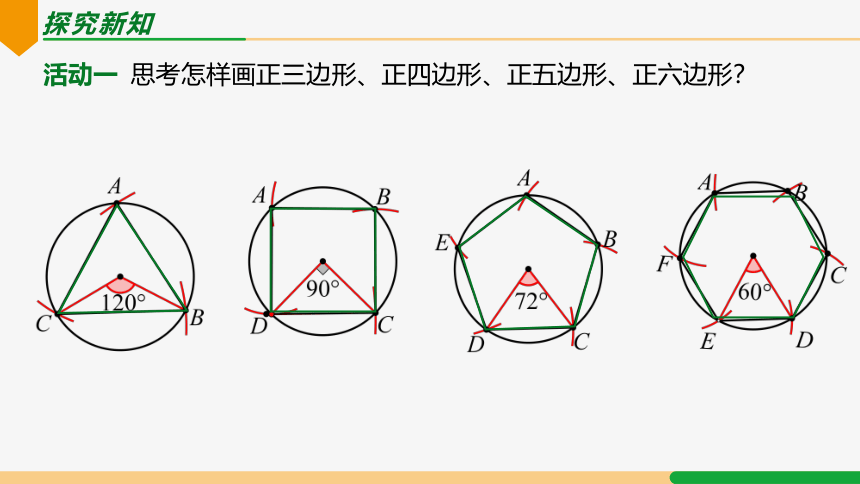
活动一 思考怎样画正三边形、正四边形、正五边形、正六边形?
活动二 尺规作图画正三边形、正四边形、正六边形.
O
A
B
C
F
D
E
知识小结
各边相等、各角相等
定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
正多边形
正多边形和圆
圆内接正多边形
辅助线
中心、中心角
半径、边心距
1. 连半径,得中心角;
2. 作边心距,构造直角三角形
正多边形作图
等分圆周
尺规作图
课堂练习
1. 在半径 R 的圆上依次截取等于 R 的弦,顺次连接各分点得到的多边形是 ( )
A.正三角 B.正方形
C.正五边形 D.正六边形
D
2. 已知正六边形 ABCDEF 内接于⊙O ,正六边形的周长是 24 ,则⊙O 的半径长是 ( )
O
30°
24÷6÷2 = 2
R
B
P
B
已知正多边形的边心距与边长的比是1:1,则此正多边形是( )
A.正三角形 B、正方形
C.正六边形 D、正十二边形
B
若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为( )
A.36° B、 18° C.72° D.54°
A
如图,M,N 分别是☉O 内接正多边形的边AB,BC 上的点,且 BM = CN.
(1) 图①中∠MON = °,图②中∠MON = °,
图③中∠MON = °;
(2) 试探究∠MON 的度数与正 n 边形的边数 n 的关系.
90
72
120
.
A
B
C
M
N
O
图①
A
B
C
D
M
N
O
图②
A
B
C
D
E
M
N
O
图③
画圆内接正多边形
24.3 正多边形和圆
| 24.3 正多边形和圆 第2课时 |
课堂导航
画圆内接正多边形
情景引入
观察:下图的这些由正边形组成的图案,怎样画正多边形。
知识回顾
各边相等、各角相等
定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
正多边形
正多边形和圆
圆内接正多边形
辅助线
中心、中心角
半径、边心距
1. 连半径,得中心角;
2. 作边心距,构造直角三角形
探究新知
活动一 思考怎样画正三边形、正四边形、正五边形、正六边形?
活动二 尺规作图画正三边形、正四边形、正六边形.
O
A
B
C
F
D
E
知识小结
各边相等、各角相等
定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
正多边形
正多边形和圆
圆内接正多边形
辅助线
中心、中心角
半径、边心距
1. 连半径,得中心角;
2. 作边心距,构造直角三角形
正多边形作图
等分圆周
尺规作图
课堂练习
1. 在半径 R 的圆上依次截取等于 R 的弦,顺次连接各分点得到的多边形是 ( )
A.正三角 B.正方形
C.正五边形 D.正六边形
D
2. 已知正六边形 ABCDEF 内接于⊙O ,正六边形的周长是 24 ,则⊙O 的半径长是 ( )
O
30°
24÷6÷2 = 2
R
B
P
B
已知正多边形的边心距与边长的比是1:1,则此正多边形是( )
A.正三角形 B、正方形
C.正六边形 D、正十二边形
B
若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为( )
A.36° B、 18° C.72° D.54°
A
如图,M,N 分别是☉O 内接正多边形的边AB,BC 上的点,且 BM = CN.
(1) 图①中∠MON = °,图②中∠MON = °,
图③中∠MON = °;
(2) 试探究∠MON 的度数与正 n 边形的边数 n 的关系.
90
72
120
.
A
B
C
M
N
O
图①
A
B
C
D
M
N
O
图②
A
B
C
D
E
M
N
O
图③
同课章节目录
