24.3 第1课时 正多边形和圆 课件(共18张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 24.3 第1课时 正多边形和圆 课件(共18张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 25.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 05:46:13 | ||
图片预览






文档简介
(共18张PPT)
正多边形和圆
24.3 正多边形和圆
| 24.3 正多边形和圆 第1课时 |
课堂导航
了解正多边形和圆的有关概念。
理解并掌握正多边形半径和边长、边心距、中心角之间的关系。
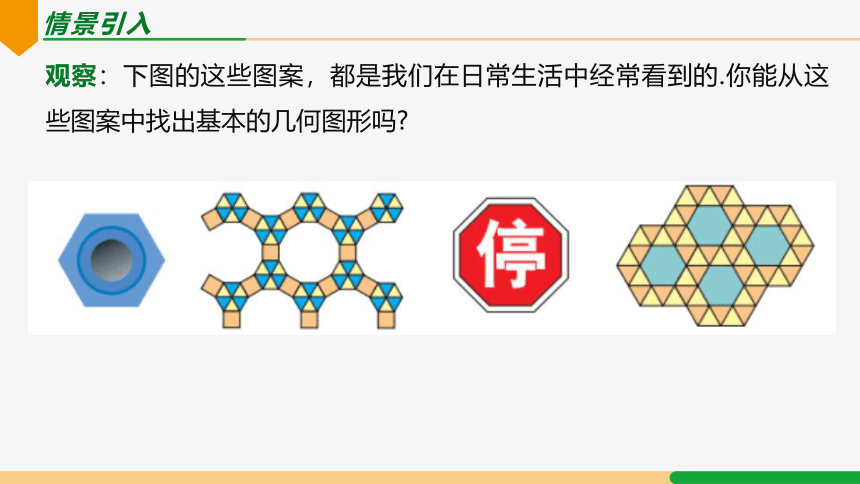
情景引入
观察:下图的这些图案,都是我们在日常生活中经常看到的.你能从这些图案中找出基本的几何图形吗
探究新知
活动一 观察以下列图形,思考
1.各图形各边和各内角什么特点?
2.这些图形与圆有什么关系?
证明:如图,把⊙O 分成相等的 5 段弧,依次连接各分点得到正五边形 ABCDE.
∴∠A =∠B. 同理 ∠B =∠C =∠D =∠E.
又∵五边形 ABCDE 的顶点都在⊙O 上,
∴五边形 ABCDE 是⊙O 的内接正五边形,⊙O 是五边形 ABCDE 的外接圆.
O
知识要点1
正多形的外接圆.
只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多形的外接圆
O
知识要点2
类比
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所对的圆心角
正多边形的中心角
圆心到弦的距离
正多边形的边心距
典例讲解
例1 如图,有一个亭子,它的地基半径为 4 m 的正六边形,求地基的周长和面积(结果保留小数点后一位).
亭子地基的面积
解:连接 OB,过点 O 作 OP⊥BC 于 P.
亭子地基的周长 l = 6×4 = 24 (m),
知识要点3
圆内接正多边形的辅助线
2. 作边心距,构造直角三角形.
1. 连半径,得中心角;
例2.正六边形的边心距为,则该正六边形的边长是( )
A. B.2 C.3 D.2
B
正多边形的边数 边长 半径 边心距 周长 面积
3 2
4 2
6 2
1
8
4
2
12
针对练习
知识小结
各边相等、各角相等
定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
正多边形
正多边形和圆
圆内接正多边形
辅助线
中心、中心角
半径、边心距
1. 连半径,得中心角;
2. 作边心距,构造直角三角形
课堂练习
如图,已知 ⊙O 的周长等于 6π,则该圆内接正六边形 ABCDEF 的边心距 OG 为 ( )
C
如图,正六边形ABCDEF 内接于 ⊙O ,点 M 在 上,则 ∠CME 的度数为 ( )
A.30°
B.36°
C.45°
D.60°
D
已知圆的半径是,则该圆的内接正六边形的面积是( )
A. B. C. D.
C
如图,已知点 O 是正六边形 ABCDEF 的对称中心,G,H 分别是 AF,BC 上的点,且 AG = BH.
(1) 求∠FAB 的度数;
(2) 求证:OG = OH.
(1) 解:∵ 六边形 ABCDEF 是正六边形,
O
∴∠FAB = .
(2) 证明:连接 OA、OB.
∵ OA = OB,
∴∠OAB =∠OBA.
∵∠FAB =∠CBA,
∴∠OAG =∠OBH.
∴△AOG≌△BOH (SAS).
∴ OG = OH.
又∵ AG = BH,
O
正多边形和圆
24.3 正多边形和圆
| 24.3 正多边形和圆 第1课时 |
课堂导航
了解正多边形和圆的有关概念。
理解并掌握正多边形半径和边长、边心距、中心角之间的关系。
情景引入
观察:下图的这些图案,都是我们在日常生活中经常看到的.你能从这些图案中找出基本的几何图形吗
探究新知
活动一 观察以下列图形,思考
1.各图形各边和各内角什么特点?
2.这些图形与圆有什么关系?
证明:如图,把⊙O 分成相等的 5 段弧,依次连接各分点得到正五边形 ABCDE.
∴∠A =∠B. 同理 ∠B =∠C =∠D =∠E.
又∵五边形 ABCDE 的顶点都在⊙O 上,
∴五边形 ABCDE 是⊙O 的内接正五边形,⊙O 是五边形 ABCDE 的外接圆.
O
知识要点1
正多形的外接圆.
只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多形的外接圆
O
知识要点2
类比
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所对的圆心角
正多边形的中心角
圆心到弦的距离
正多边形的边心距
典例讲解
例1 如图,有一个亭子,它的地基半径为 4 m 的正六边形,求地基的周长和面积(结果保留小数点后一位).
亭子地基的面积
解:连接 OB,过点 O 作 OP⊥BC 于 P.
亭子地基的周长 l = 6×4 = 24 (m),
知识要点3
圆内接正多边形的辅助线
2. 作边心距,构造直角三角形.
1. 连半径,得中心角;
例2.正六边形的边心距为,则该正六边形的边长是( )
A. B.2 C.3 D.2
B
正多边形的边数 边长 半径 边心距 周长 面积
3 2
4 2
6 2
1
8
4
2
12
针对练习
知识小结
各边相等、各角相等
定理
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角
正多边形
正多边形和圆
圆内接正多边形
辅助线
中心、中心角
半径、边心距
1. 连半径,得中心角;
2. 作边心距,构造直角三角形
课堂练习
如图,已知 ⊙O 的周长等于 6π,则该圆内接正六边形 ABCDEF 的边心距 OG 为 ( )
C
如图,正六边形ABCDEF 内接于 ⊙O ,点 M 在 上,则 ∠CME 的度数为 ( )
A.30°
B.36°
C.45°
D.60°
D
已知圆的半径是,则该圆的内接正六边形的面积是( )
A. B. C. D.
C
如图,已知点 O 是正六边形 ABCDEF 的对称中心,G,H 分别是 AF,BC 上的点,且 AG = BH.
(1) 求∠FAB 的度数;
(2) 求证:OG = OH.
(1) 解:∵ 六边形 ABCDEF 是正六边形,
O
∴∠FAB = .
(2) 证明:连接 OA、OB.
∵ OA = OB,
∴∠OAB =∠OBA.
∵∠FAB =∠CBA,
∴∠OAG =∠OBH.
∴△AOG≌△BOH (SAS).
∴ OG = OH.
又∵ AG = BH,
O
同课章节目录
